Vibration of thin elastic FGM plates with multi-gradation effects

Sator, Ladislav; Sladek, Vladimir; Sladek, Jan

doi:10.21595/vp.2019.20707

Vibroengineering Procedia

Browse Procedia

Published: 25 April 2019

Check for updates

Vibration of thin elastic FGM plates with multi-gradation effects

Ladislav Sator¹

Vladimir Sladek²

Jan Sladek³

^{1, 2, 3}Institute of Construction and Architecture, Slovak Academy of Sciences, Bratislava, Slovakia

Corresponding Author:

Ladislav Sator

Cite the article Download PDF

Downloads 1323

Abstract

In this paper we investigate the vibration response of thin elastic FGM plates with combination of transversal and/or in-plane gradation of various material parameters subjected to transient tension loading. The equations of motion and initial-boundary conditions for transient problems are derived within Kirchhoff-Love plate theory. For numerical modelling of plates with dynamic multi-gradation coupling effects, it is developed the strong formulation with using the meshless approximation of field variables by the Moving Least Square (MLS) approximation scheme. Several numerical examples are presented for illustration of the multi-gradation coupling effects in vibration response of elastic FGM plates.

1. Introduction

Plates are considered as the fundamental structural elements within the civil, mechanical and aerospace engineering. The small aspect ratio of thickness to length justifies to make certain assumptions about the deformation of plates with resulting into conversion of originally 3D elasticity problems into 2D problems with important simplifications in study the response of plate structures to static as well as dynamic loadings [1-3].

The design of modern structures often utilizes the benefits offered by composition of two or more materials. Classical laminated composite plate structures suffer from delamination due to the in-plane stress discontinuities on interfaces. This unpleasant effect is eliminated in the FGM composite plates, in which the material properties are varying continuously according to volume contents of particular micro-constituents [4] and there are no interfaces. The functional gradation of material coefficients in FGM composites can be modelled successfully by the rule of mixture [5] in the case of two component micro-composites.

It should be stressed that a correct formulation of the boundary value problems for FGM plates cannot be obtained from the formulation derived for homogeneous plates by simple consideration of spatial variations of material coefficients. It has been shown that the transversal gradation of the Young’s modulus and/or mass density yields coupling between the bending and in-plane deformation modes in plates subjected to transversal loading. Moreover, it has been shown [6] that the combined gradation of material coefficients in the transversal and in-plane directions into multi-gradation coupling effects in plates subjected to stationary transversal and/or tension loadings. The main goal of this paper is to study the multi-gradation coupling effects in plates subjected to transient tension loads.

The equations of motion for bending of thin elastic plates within the classical Kirchhoff-Love theory are given by the 4th order partial differential equations (PDE). It is well known that the accuracy of approximations of derivatives of field variables is decreasing with increasing the order of the derivatives. This inconvenience can be overcome by decomposing the original PDE into the system of PDE with lower order of derivatives [7]. Combination of the strong formulation with compactly supported meshless MLS-approximation of spatial variations of field variables [8] results into an efficient computational technique, when the original PDE are converted into the system of the ordinary differential equations (ODE) for nodal unknowns. In this paper, we have employed the standard Wilson $θ$ -method [9,10] for numerical solution of the derived ODEs.

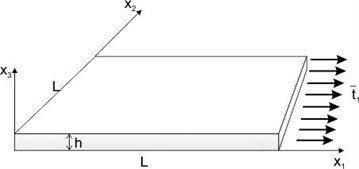
Several numerical examples are presented to investigate the vibration response of the FGM plates. The coupling effects are studied for FGM plates under external tension load on the plate’s boundary edge (Fig. 1).

Fig. 1Square FGM plate loaded by pure in-plane loading

2. Equations of motion

Let us consider factorized gradations of material coefficients in the transversal and in-plane directions. Then the derivation of 2D formulation for plate bending problems is possible to be accomplished in closed form. Furthermore, we assume the power-law gradations of the Young’s modulus and mass density in both the vertical and horizontal directions:

1

E_{V}^{} (x_{3}) = 1 + ζ {(\frac{1}{2} \pm \frac{x_{3}}{h})}^{p}, ζ = \frac{E (\pm h / 2)}{E_{0}} - 1, E_{0} = E (\mp \frac{h}{2}),

ρ_{V}^{} (x_{3}) = 1 + η {(\frac{1}{2} \pm \frac{x_{3}}{h^{}})}^{r}, η = \frac{ρ (\pm h / 2)}{ρ_{0}} - 1, ρ_{0} = ρ (\mp \frac{h}{2}),

2

E_{H}^{*} (x_{1}) = 1 + ε {(x_{1})}^{α}, ρ_{H}^{*} (x_{1}) = 1 + ψ {(x_{1})}^{ω} .

Since the problem is considered within the linear theory, it is appropriate to define the dimensionless coordinates and time variable as:

3

x_{β}^{*} : = \frac{x_{β}}{L}, x_{3}^{*} : = \frac{x_{3}}{h_{0}} = h^{*} (x) z, h (x) = h_{0} h^{*} (x), t^{*} : = \frac{t}{T},

with $L$ , $h_{0}$ , $T$ being the characteristic in-plane dimension, plate thickness and time interval. The dimensionless field variables in the KLT are introduced as:

4

u_{β}^{*} (x, t) : = \frac{u_{β} (x, t)}{h_{0}}, w^{*} (x, t) : = \frac{w (x, t)}{h_{0}},

where we have omitted the superscript $*$ in coordinates and time variable.

Combination of the Hamilton principle with assumptions of the KLT for thin plates results into the set of the equations of motion:

5a

\{C_{, β}^{(u u)} (x) τ_{α β}^{* (u)} (x, t) + C^{(u u)} (x) τ_{α β, α}^{* (u)} (x, t) + C_{, β}^{(u w)} (x) τ_{α β}^{* (w)} (x, t) + C^{(u w)} (x) τ_{α β, α}^{* (w)} (x, t)\}

+ D^{(u u)} (x) {\ddot{u}}_{α}^{*} (x, t) + D^{(u w)} (x) {\ddot{w}}_{, α}^{*} (x, t) = 0,

5b

\{C_{, α β}^{(w u)} (x) τ_{α β}^{(u)} (x, t) + C_{, β}^{(w u)} (x) τ_{α β, β}^{(u)} (x, t) + C^{(w u)} (x) τ_{α β, α β}^{(u)} (x, t) + C_{, α β}^{(w w)} (x) τ_{α β}^{(w)} (x, t) + 2 C_{, β}^{(w w)} (x) τ_{α β, β}^{(w)} (x, t) + C^{(w w)} (x) τ_{α β, α β}^{(w)} (x, t)\}

+ D^{(w u)} (x) {\ddot{u}}_{β}^{*} (x, t) + D_{1}^{(w w)} (x) {\ddot{w}}^{*} (x, t) + {(D_{2}^{(w w)} (x) {\ddot{w}}_{, β}^{*} (x, t))}_{, β} = - q^{*} (x, t),

and the boundary restrictions, which can be satisfied on the clamped sliding plate edge by obeying the boundary conditions:

6

n_{β} {T_{α β}^{*}|}_{x_{1} = L} = {h^{*}|}_{x_{1} = L} σ^{*} δ_{α 1} = {h^{*} {\bar{t}}_{α}^{*}|}_{x_{1} = L}, {u_{1}^{*} (x, t)|}_{x_{1} = 0} = 0 \land n_{β} {T_{2 β}^{*}|}_{x_{1} = 0} = 0,

n_{β} {T_{α β}^{*}|}_{x_{2} \in {0, L}} = 0, {w^{*} (x, t)|}_{\partial Ω} = 0, {\frac{\partial w^{*}}{\partial n} (x, t)|}_{\partial Ω} = 0 .

In the equations of motion, we have used the following notations for the deformation fields:

7a

τ_{α β}^{* (u)} (x, t) = \frac{H}{2} (u_{α, β}^{*} (x, t) + u_{β, α}^{*} (x, t)) + ν δ_{α β} u_{γ, γ}^{*} (x, t),

7b

τ_{α β}^{* (w)} (x, t) : = H w_{, α β}^{*} (x, t) + ν δ_{α β} \nabla^{2} w^{*} (x, t),

and the explicit expressions for the coefficients $C^{(\cdot)}$ , $D^{(\cdot)}$ can be found in [11].

To eliminate the high order derivatives of field variables in equations of motion, we decompose the original 4th order PDEs Eq. (5) into the coupled set of 2nd order PDEs by introducing new field variables as:

8

m^{*} (x, t) : = \nabla^{2} w^{*} (x, t), s_{α}^{*} (x, t) : = \nabla^{2} u_{α}^{*} (x, t) .

Then, we have:

9a

τ_{α β, β}^{* (u)} (x, t) = \frac{H}{2} s_{α}^{*} (x, t) + \frac{H + 2 ν}{2} u_{β, β α}^{*} (x, t), τ_{α β, α β}^{* (u)} (x, t) = (H + ν) s_{β, β}^{*} (x, t),

9b

τ_{α β, β}^{* (w)} (x, t) = (H + ν) m_{, α}^{*} (x, t), τ_{α β, α β}^{* (w)} (x, t) = (H + ν) \nabla^{2} m^{*} (x, t) .

Substituting Eqs. (7) and (9) into Eq. (5), we receive 3 equations which together with Eq. (8) give the complete set of governing equations for the primary field variables $\{w^{*} (x, t), m^{*} (x, t), u_{β}^{*} (x, t), s_{β}^{*} (x, t)\}$ .

3. Moving least squares (MLS) approximation technique

The Central Approximation Node (CAN) concept of standard MLS approximation technique yields a compactly supported meshless approximation for spatial variations of field variables, in which $x^{q}$ is considered as the CAN for the approximation at a point $x$ . Then, the number of nodes $N^{q}$ supporting the approximation at $x$ is smaller than the total number of nodes $N$ . Without going into details [7, 12, 13], the MLS-CAN approximation for a field variable $u (x, t)$ is given as:

10

u (x, t) \approx \sum_{a = 1}^{N^{q}} {\hat{u}}^{\bar{a}} (t) ϕ^{(q, a)} (x), \bar{a} = n (q, a),

where $\bar{a}$ is the global number of the $a$ -th node from the $N^{q}$ nodal points supporting the approximation at the CAN node, which can be selected as the nearest node to the field point $x$ .

The derivatives of the field variable $u (x)$ can be approximated in a standard way by differentiating the approximation Eq. (10), i.e.:

11

u_{, i} (x, t) \approx \sum_{a = 1}^{N^{q}} {\hat{u}}^{\bar{a}} (t) ϕ_{, i}^{(q, a)} (x), u_{, i j} (x, t) \approx \sum_{a = 1}^{N^{q}} {\hat{u}}^{\bar{a}} (t) ϕ_{, i j}^{(q, a)} (x) .

4. Numerical experiments

For numerical tests and study of coupling effects, we considered a thin square plate $L \times L$ with clamped all the edges and constant thickness $h = L / 50$ , where $L = 1$ m. The plates are either homogeneous or FGM with power-law graded Young’s modulus and/or mass density. Poisson’s ratio is assumed to be constant $ν =$ 0.3, while various values of the power-law gradation exponent and levels of gradation are considered. The external shock tension load ${{\bar{t}}_{1}^{*}|}_{L} = H (t)$ is applied.

In all numerical computations, we have used a uniform distribution of nodal points (16×16 nodes) with $δ$ being the distance between two neighbour nodes. The other parameters in the MLS-approximation with Gaussian weights have been taken as: radius of the interpolation domain $ρ^{a} = 3.001 δ$ , shape function parameter $c^{a} = δ$ , and cubic polynomial basis.

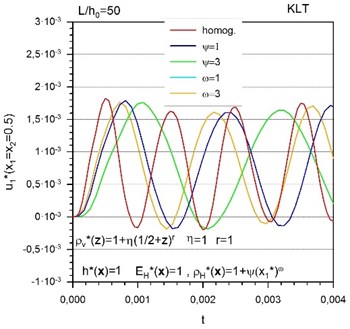
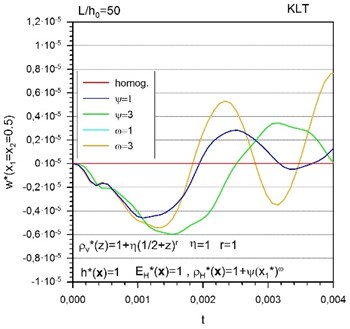
The coupling between the bending and in-plane deformation modes is clearly seen in FGM plates (Figs. 2-4). Finite deflections can be observed in FGM plates subjected to in-plane tension, while in the homogeneous plate no deflection response is observed. It is necessary to note that in the case of pure transversal gradation the deflection response is negligible.

Fig. 2Time variation of a) in-plane displacements and b) deflections of FGM plates with simultaneous transversal and in-plane gradation of Young’s modulus

Time variation of a) in-plane displacements and b) deflections of FGM plates with simultaneous transversal and in-plane gradation of Young’s modulus

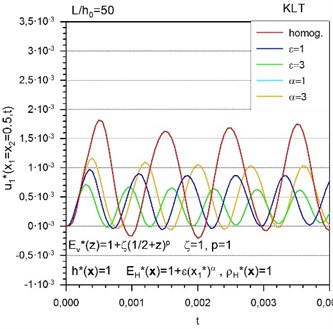
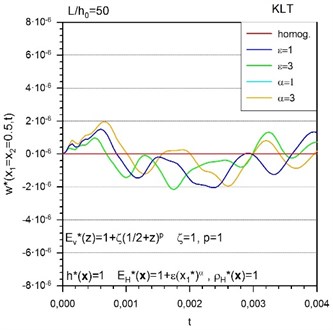
Fig. 3Time variation of a) in-plane displacements and b) deflections of FGM plates with simultaneous transversal gradation of mass density and in-plane gradation of Young’s modulus

Time variation of a) in-plane displacements and b) deflections of FGM plates with simultaneous transversal gradation of mass density and in-plane gradation of Young’s modulus

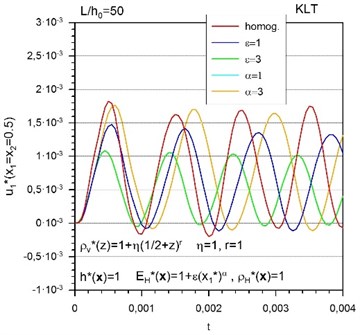
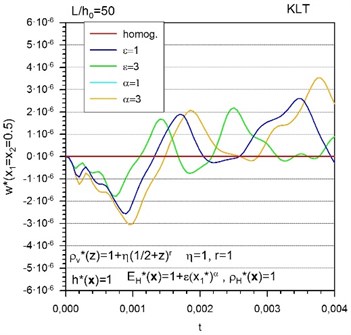
Fig. 2 shows the in-plane displacements and deflections in thin FGM plates with combined transversal and in-plane gradations of Young’s modulus for various levels and/or exponents of in-plane gradation. It can be seen that the frequencies of vibrations in the FGM plates are higher than in the homogeneous plate and the maximum amplitude is decreasing with the increasing value of level of gradation. The influence of the exponent of gradation of Young’s modulus on the vibration response is also observable. With increasing the exponent of the in-plane gradation of Young’s modulus the frequency of vibrations is decreasing.

On Fig. 3, there is presented the vibration response of FGM plate with combined transversal gradation of mass density and in-plane gradation of Young’s modulus. The response of the plate is similar as in the case of FGM plate with combined transversal and in-plane gradations of Young’s modulus. However, due to the increasing value of mass density the frequency of vibration is not increasing so significantly.

The influence of the combination of transversal and in-plane gradation of the mass density on the in-plane displacements and deflections is seen from Fig. 4. Since the bending stiffness is unchanged, the amplitudes are not affected but the frequency of vibrations is decreasing with increasing level of gradation of the mass density. It can be clearly seen that the transversal gradations of the Young’s modulus and mass density result in opposite effects on the frequency of vibrations.

Fig. 4Time variation of a) in-plane displacements and b) deflections of FGM plates with simultaneous transversal and in-plane gradation of mass density

Time variation of a) in-plane displacements and b) deflections of FGM plates with simultaneous transversal and in-plane gradation of mass density

5. Conclusions

In this paper, we developed a mathematical formulation for mechanical analysis of elastic FGM plates with multi-gradations of Young’s modulus and/or mass density. The in-plane gradation of material coefficients leads to the rather complex PDE with variable coefficients. The proposed combination of the compactly supported meshless approximation with strong formulation and Wilson $θ$ -method together with decomposition of the high order derivative PDE into the system of lower order PDE yields a computationally efficient method for this class of problems. In the presented numerical simulations, we revealed and discussed a new class of dynamic coupling effects evoked by multiple gradations of material coefficients in FGM plates subjected to in-plane transient tension loading.

References

Barber J. R. Elasticity. Springer Science+Business Media B.V., New York, 2010.

Search CrossRef
Reddy J. N. Mechanics of Laminated Composite Plates: Theory and Analysis. CRC Press, Boca Raton, 1997.

Search CrossRef
Timoshenko S. P., Woinowsky Krieger S. Theory of Plates and Shells. McGraw-Hill, New York, 1959.

Search CrossRef
Suresh S., Mortensen A. Fundamentals of Functionally Graded Materials. Institute of Materials, London, 1998.

Search CrossRef
Ardestani M. M., Soltani B., Shams S. Analysis of functionally graded stiffened plates based on FSDT utilizing reproducing kernel particle method. Composite Structures, Vol. 112, 2014, p. 231-240.

Publisher
Sladek V., Sator L., Sladek J. Multiple gradations coupling effects in the bending of thin elastic FGM plates. WIT Transactions on Modelling and Simulation, Vol. 61, 2015, p. 223-234.

Publisher
Sladek V., Sladek J., Sator L. Physical decomposition of thin plate bending problems and their solution by mesh-free methods. Engineering Analysis with Boundary Elements, Vol. 37, 2013, p. 348-365.

Publisher
Lancaster P., Salkauskas K. Surfaces generated by moving least squares method. Mathematics of Computation, Vol. 37, 1981, p. 141-158.

Publisher
Wilson E. L., Farhoomand I., Bathe K. J. Nonlinear dynamic analysis of complex structures. Earthquake Engineering and Structural Dynamics, Vol. 1, 1973, p. 241-252.

Publisher
Gladwell I., Thomas R. Stability of the Newmark, Houbolt and Wilson θ methods. International Journal for Numerical and Analytical Methods in Geomechanics, Vol. 4, 1980, p. 143-158.

Publisher
Sator L., Sladek V., Sladek J. Elastodynamics of FGM plates by mesh-free method. Composite Structures, Vol. 140, 2016, p. 309-322.

Publisher
Sladek V., Sladek J., Zhang C. Computation of stresses in non-homogeneous elastic solids by local integral equation method: a comparative study. Computational Mechanics, Vol. 41, 2008, p. 827-845.

Publisher
Sladek V., Sladek J., Zhang C. Local integral equation formulation for axially symmetric problems involving elastic FGM. Engineering Analysis with Boundary Elements, Vol. 32, 2008, p. 1012-1024.

Publisher

About this article

Received

21 March 2019

Accepted

02 April 2019

Published

25 April 2019

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/vp.2019.20707

Keywords

FGM plate

strong formulation

Kirchhoff-Love theory

meshless methods

moving least square approximation scheme

transient analysis

Acknowledgements

The financial support of the Slovak Research and Development Agency under the contract No. APVV-14-0440 is greatly acknowledged.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2019 11 28

Free vibration analysis of simply supported rectangular plates

Ganesh Naik Guguloth, Baij Nath Singh, Vinayak Ranjan

Research article

2019 11 28

Dynamic stiffness method for free vibration analysis of thin functionally graded rectangular plates

Manish Chauhan, Vinayak Ranjan, Prabhakar Sathujoda

Research article

2019 03 15

Modelling on vibration of skew plate with thickness and temperature variation

Reeta Bhardwaj, Naveen Mani

Research article

2018 12 13

Free vibration analysis of FGM plates based on Rayleigh-Ritz method

Jun Zhang, Tianyun Li, Xiang Zhu

L. Sator, V. Sladek, and J. Sladek, “Vibration of thin elastic FGM plates with multi-gradation effects,” Vibroengineering PROCEDIA, Vol. 23, pp. 24–29, Apr. 2019, https://doi.org/10.21595/vp.2019.20707

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2019.20707
UR  - https://doi.org/10.21595/vp.2019.20707
TI  - Vibration of thin elastic FGM plates with multi-gradation effects
T2  - Vibroengineering PROCEDIA
AU  - Sator, Ladislav
AU  - Sladek, Vladimir
AU  - Sladek, Jan
PY  - 2019
DA  - 2019/04/25
PB  - JVE International Ltd.
SP  - 24-29
VL  - 23
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Sator_2019,
	doi = {10.21595/vp.2019.20707},
	url = {https://doi.org/10.21595/vp.2019.20707},
	year = 2019,
	month = {apr},
	publisher = {{JVE} International Ltd.},
	volume = {23},
	pages = {24--29},
	author = {Ladislav Sator and Vladimir Sladek and Jan Sladek},
	title = {Vibration of thin elastic {FGM} plates with multi-gradation effects},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]L. Sator, V. Sladek, and J. Sladek, “Vibration of thin elastic FGM plates with multi-gradation effects,” Vibroengineering PROCEDIA, vol. 23, pp. 24–29, Apr. 2019, doi: 10.21595/vp.2019.20707.

Copy IEEE

Copied to clipboard!

Sator, Ladislav, Vladimir Sladek, and Jan Sladek. “Vibration of Thin Elastic FGM Plates with Multi-Gradation Effects.” Vibroengineering PROCEDIA 23 (April 25, 2019): 24–29. https://doi.org/10.21595/vp.2019.20707.

Copy Chicago

Copied to clipboard!

Vibration of thin elastic FGM plates with multi-gradation effects

Abstract

1. Introduction

2. Equations of motion

3. Moving least squares (MLS) approximation technique

4. Numerical experiments

5. Conclusions

References

About this article

Related Articles