Remaining useful life (RUL) prediction of bearing by using regression model and principal component analysis (PCA) technique

1. Introduction

With the growing impact of climate change Renewable energy remains the only viable option to save the motherland. With India’s aim to achieve 175GW of installed capacity of renewable energy by 2020 wind energy provides one of the most potential sector. India has the 4th largest installed capacity of wind turbines in the world. We still lack to achieve to our full potentials due to unresolved failures like that of failure of a gearbox, an integral part of producing wind energy. Power output can be increased by early detection of faults by fault prognosis and condition monitoring. Prognostics forecast the performance of an element surveying the degree of deviation or degradation of a system from its typical operating conditions. The predicted time is known as the Remaining Useful Life (RUL), with accurate RUL reduction in the inspection as well as maintenance cost is observed, which further contributes in expanding the general proficiency of the plant. Predicting an approaching failure and estimating the RUL of a bearing is necessary for coming up with support and sidestepping sudden shutdowns of basic frameworks. This paper exhibits a hybrid method for prognosis of bearing which makes used of regression primarily based adaptive predictive models to gain proficiency with the advancing pattern tendency in a bearing’s health indicator. These models are then used to project forward in time and estimate the RUL of a bearing [1].

Prognostics is mainly distributed as: model-based prognostics and data-driven prognostics. Model-based prognostics attempts to incorporate physical modeling at material level while mathematical modeling at the system level with different system variables used into the estimation of RUL. Systems are complex, which arises the need for highly skilled labors, hence making it time-consuming and labor- intensive method. Whereas data-driven prognostics concentrates on the available system monitoring data. Here, failure prognosis includes prognostication of system degradation and time-to-failure supported on “state awareness” gathered from monitored information [2]. The machine learning (ML) market is rising speedily in light of the Internet insurgency and deployment of ML improves the speed and exactness of capacities performed by the framework. A ton of research work is carried out on foreseeing the RUL of bearing utilizing a machine learning approach. However, the outcome appeared by the majority of this paper isn't remarkable. Developing interest for artificial intelligence and outstanding advancements in its improvement has encouraged plenty of researchers to use this approach in the prediction of bearing RUL. Traditional methods like Support Vector Machines (SVM) [3, 4] and Principal Component Analysis (PCA) [5, 6]. Nonetheless, SVM is sensitive to feature scaling and tend to overfit for big datasets. The prediction of feature scaled dataset has low accuracy due to limited available range in our case. Researchers have also used various forms of ANN for bearing RUL prediction [7, 8]. The ensemble of BP-ANN used by Zhang et al. has also been verified through experimental data [9]. Ensembles are widely utilized in the domain of reliability in the past as they turn out to be vastly improved than alternate models. Stacking ensemble of ANN and Gradient Boosted Trees (GBT) work better than CNN, SVM, GBT, and MLP, as shown by Sandip et al. in his work on prognostics [10].

In this paper, Dataset utilized for the investigation is taken by IEEE PHM Data Challenge 2012 for FEMTO bearing informational collection [11]. The methodology contains extraction of the statistical features in $X$ and $Y$ direction, features ranking is done utilizing a PCA approach which is furthermore used to make distinctive datasets. The appropriate scoring function is taken to figure the score of models using error between actual RULs and values predicted for test bearings.

2. Theory

3. Experimentation

The dataset used for the analysis is taken by IEEE PHM Data Challenge 2012 for FEMTO bearing data-set. Containing failure data of REB data obtained from a PRONOSTIA platform for 17 runs to failure. Collection of data is done by the test rig shown in the Fig. 1. Use of two accelerometers was done to gather the data. The useful life of the bearing is considered to end when the amplitude of the vibration signal reaches 20 g.

Fig. 1Experimental set-up [11]

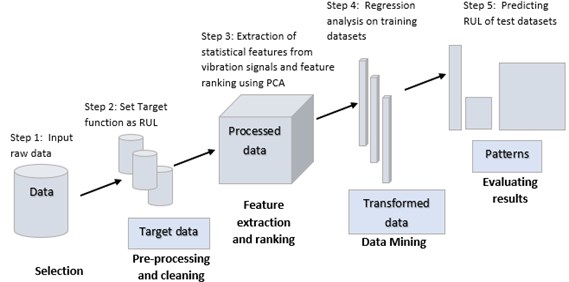
4. Methodology

The proposed methodology in this paper is shown in Fig. 2.

STEP 1: Input data is acquired by IEEE PHM Data challenge 2012 - FEMTO bearing data set.

STEP 2: Target function – Assumption: Last cycle = Failure cycle:

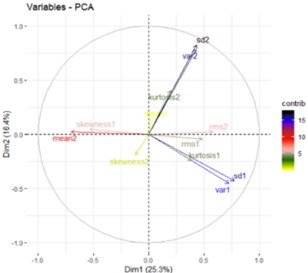
STEP3: Extraction of statistical features and doing feature ranking Fig. 3.by PCA method. Ranking of RPM and load are considered as immaterial.

STEP 4: Datasets were created using their rank which were further used to create data frames for regression analysis.

STEP 5: Similar datasets were created for the testing data and RUL is predicted for each test bearing. Error and score calculations are done for the predicted RUL.

Fig. 2Methodology used for prediction of RUL

4.1. Feature ranking and feature set formation

Principal component analysis (PCA) is used to recognize the contribution of features that are most adding to the principal components. It uses a variance ratio for ranking the given features. Variance is calculated using:

4

$\sigma =\sum j\lambda j.$

So, variance ratio ($rj$) for the given component $j$ is calculated the following formula:

5

$rj=\frac{\lambda j}{\sigma }.$

Using ranked features, 12 feature sets were made so that the first feature set contains the first top-ranked feature, at that point the second feature set contains the top two ranked features and so on. It enables to test the importance of features and the overall accuracy of the system.

Fig. 3Feature ranking using PCA

5. Result

RUL is calculated for the proposed model and results obtained are discussed below. Error in the predicted and actual RUL is calculate using following formula:

The scoring function used is as follows:

The overall score is calculated using:

Fig. 4Trend of scores of feature datasets

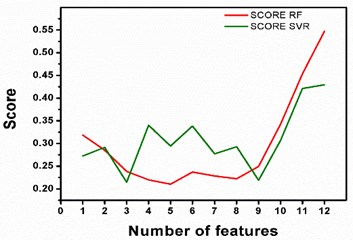
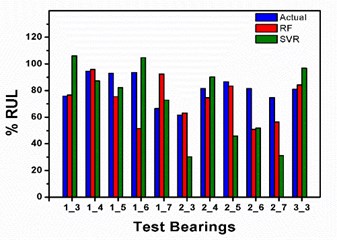
Fig. 5Comparison between regression models for 12 features dataset

In the present study SVR and RF models are employed to predict RUL of bearing. firstly, features are extracted from IEEE PHM Data Challenge 2012 bearing dataset and ranked using PCA, which are further used to form training and testing input feature sets. Fig. 4. depicts the graph of calculated scores using SVR and RF as per mathematical expression given in data sheet. For RF regression model, the score is indicating lessening pattern till 8 features dataset however it rockets up with the expansion in the features and finally both the models achieve highest score with 12th feature set and score with RF outperforms SVR. Fig. 5.

Displays comparison between actual RUL and RUL computed using the regression models of IEEE FAMTO data set. Fig. 5. demonstrates the relative investigation between the 2 models using 12 features datasets with the actual value anticipated. The score of the SVR model is 0.429582 which is most reduced while the RF model is indicating most astounding score estimation of 0.547452. Table 3 contains the values of bearing’s actual RUL and predicted RUL to calculate score. The highest score of 0.547452 is achieved with 12th feature set and RF.

6. Conclusions

Dataset utilized for the investigation is taken by IEEE PHM Data Challenge 2012 for FEMTO bearing informational collection. The methodology contains extraction of the statistical features in $X$ and $Y$ direction, features are ranked using a PCA approach which is additionally used to make distinctive datasets utilizing feature ranking. The outcome demonstrates RF regression is more exact than SVR models. The best score 0.5474 is accomplished utilizing RF regression mode with 12 features dataset. The result indicates the potential use of group regression procedure for a forecast of RUL.