Abstract
In order to design the optimal size of carbon fiber collapsible hinge for space engineering application, the modal and folding analysis of carbon fiber collapsible hinge is carried out in this paper. Natural frequencies and mode shapes are investigated through finite element model. The result is also verified by modal experiments. The maximum stress during folding process of the hinge is obtained by quasi-static simulation analysis. In order to increase the stiffness and stability of this collapsible structure, the fundamental frequency and maximum stress are optimized with respect to the hinge size. A co-simulation optimal design method is proposed in this paper. The optimal hinge size is obtained through non-dominated sorting genetic algorithm based on radial basis function neural network surrogate model. The fundamental frequency is increased by 12 %, while the maximum stress is decreased by 13 % after optimal design.
1. Introduction
Skillful applications of composite materials are crucial to the development of modern aerospace engineering technology. Carbon fiber composite materials are widely used for higher stiffness and lower weight compared with traditional materials. The carbon fiber collapsible hinge is currently applied in many aerospace structures, such as frame of solar array and deployable structure of satellite antenna [1-3]. Stiffness and stability of this structure are mostly concerned about during engineering application. The size of the hinge and the properties of composite materials such as laminate orientations and stack sequences are crucial to the stiffness and stability which are investigated by many researchers [4-7]. The elastic deformation of hinge provides driving force during deploying process. So plastic deformation must not occur when folding up. The stiffness is depending on the fundamental frequency, while the elastic deformation is reflected by the maximum stress. So, this paper focuses on the analysis of fundamental frequency and maximum stress. The fundamental frequency is obtained through finite element model and verified by modal experiments. Restricted to difficulties of experiment, the value of maximum stress is obtained through quasi-static analysis based on finite element model.
Based on the modal and folding analysis, this paper provides a co-simulation optimal design method for solution of optimal size of the hinge. Because of the large amount of time cost on the calculation of finite element model, the surrogate model is built for optimization iteration based on Latin hypercube sample algorithm. Many researchers have investigated the optimization based on various algorithm [8-10]. Radial basis function neural network is chosen as surrogate model to reflect the nonlinear relationships between the optimization objectives and variables. The optimal size of the hinge is obtained through this surrogate model based on non-dominated sorting genetic algorithm.
2. Modal analysis
2.1. Finite element model of carbon fiber collapsible hinge
The finite element model of carbon fiber collapsible hinge is built based on ABAQUS composite materials processing module shown in Fig. 1. A single layer composite can be considered as a transversely isotropic homogeneous material. The elastic properties are defined based on five lamina engineering coefficients. is longitudinal elastic modulus of each composite materials layer. is transverse elastic modulus. is longitudinal Poisson’s ratio. and are shear elastic modulus. The material properties of hinge are shown in Table 1. In order to eliminate the effect of coupling between extension and bending. The hinge is composed of ten carbon fiber composite material layers which stacked orthogonally and symmetrically as . The thickness of each layer is 0.1 mm. The model is meshed as reduced integration shell elements shown in Fig. 1. The value of fundamental frequency extracted through linear perturbation analysis step is 133 HZ under free vibration by using ABAQUS.
Fig. 1Finite element model of carbon fiber collapsible hinge

Table 1Material properties of hinge
Density (g/cm3) | 1.78 | |
Elastic modulus (GPa) | 126 | |
8 | ||
0.26 | ||
3.70 | ||
3.08 | ||
2.2. Modal experiment
As it shown in Fig. 2, the free modal experiment is carried out to verify the results of finite element model. The hinge is hung up to ensure the free boundary conditions. Hammering modal method is carried out to analyze free vibration of the hinge. There are 11 output points distributed on the axial direction of the hinge. The exciting position is set at the end of the hinge. The vibration signal is acquired through one-direction acceleration sensor fixed on the test output points. The signal collector is VibPilot-8 made by M+P international company. The vibration signal is analyzed by M+P international SO analyzer software. The fundamental frequency obtained based on the modal experiment is 135 HZ. The relative error between finite element model and experiment is small enough. Also, the first mode shape acquired through finite element model is in good agree with result of modal experiment.
Fig. 2Free modal experiment of hinge

3. Quasi-static folding analysis
Before launched into space, the hinge is folded and packed. The elastic deformation of hinge provides driving force for deployment. So, there must not be any plastic deformation during folding process. That demands the maximum stress during folding process must be smaller than the limitation of elastic deformation. In order to obtain the precise value of maximum stress, the folding process must be quasi-static. Restricted to the experiment conditions, most researchers analyze the folding process based on finite element simulation [11].
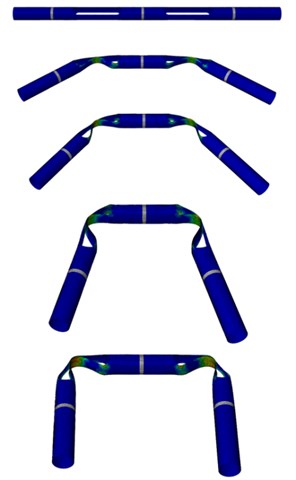
The value of maximum stress is obtained based on dynamic explicit analysis step through ABAQUS. The whole quasi-static folding process is shown in Fig. 3. The shading of color indicates different values of element stress. The red element represents the maximum stress. As it shown in the Fig. 3, the maximum stress occurs at the corners of the hinge slots and the middle of tape springs. The corners bear extrusion pressure during the folding process, while the bottom tape springs bear buckling pressure. So, the stress of the corner and the middle elements must be smaller than the limitation of plastic deformation. Based on the quasi-static analysis, the maximum stress during the folding process is 1145 MPa. The carbon fiber materials will not occur any plastic deformation under this pressure.
Fig. 3Quasi-static folding process of hinge
4. Optimal design of the hinge size
4.1. Flow chart of optimization
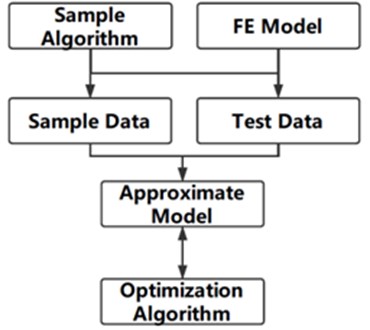
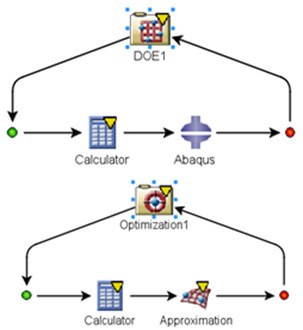
The size of the hinge is crucial to the fundamental frequency of the structure and the maximum stress when folding. In order to increase the stiffness of the structure and reduce the maximum stress, the optimal design of the size of the slots is carried out in this paper. The calculation based on finite element model cost tremendous amounts of time, especially using dynamic explicit step to analyze quasi-static folding process. So surrogate model is built for optimization iteration instead of finite element model by using co-simulation software ISIGHT. The sample algorithm is Latin hypercube. Radial basis function neural network is chosen as surrogate model to reflect the nonlinear relationships between the optimization objectives and variables. The flow chart of optimization is shown in Fig. 4.
Fig. 4Flow chart of optimization
a)
b)
4.2. Optimization model
The fundamental frequency of the structure and the maximum stress during the folding process are optimization objectives. The aim of the optimization design is to increase while decrease . The total objective is shown in Eq. (1), while and are object weights. This multi-objectives optimization is carried out based on non-dominated sorting genetic algorithm. The design variables of the optimization are the length of slot , the width of slot and the diameter of the tube hinge . The range of the design variables is shown in Table 2. The mass of the whole hinge must not be bigger than the mass before optimization. So, the constrains of optimization is shown in Eq. (2):
Table 2Design variables
Variables | (mm) | (mm) | (mm) |
Initial value | 140 | 40 | 50 |
Upper value | 100 | 30 | 46 |
Lower value | 180 | 45 | 60 |
4.3. Sensitivity analysis and optimization results
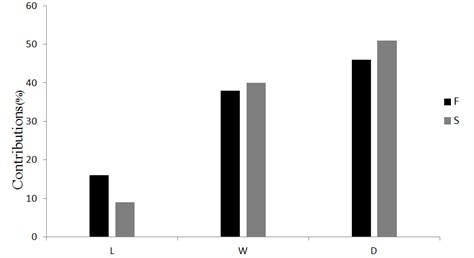
The sensitivity analysis is based on the sample data obtained from finite element model through ABAQUS based on Latin hypercube sample algorithm. As it shown in Fig. 5, the most critical parameter to the fundamental frequency and maximum stress is the diameter of the tube hinge . Then the width of the slots is the second influential parameter to the and . While the length of the slots contributes least to the and .
Table 3Pareto solutions of optimization
(mm) | (mm) | (mm) | (HZ) | (MPa) |
164 | 35 | 49 | 147 | 968 |
178 | 32 | 48 | 156 | 1012 |
170 | 33 | 48 | 151 | 995 |
The non-dominated sorting genetic algorithm is chosen as optimization algorithm with 50 generation and 30 samples of each generation. The results of this multi-objectives optimization are Pareto solutions shown in Table 3. The optimal result contains three noninferior solutions. The fundamental frequency is increased by 9 %-16 %, while the maximum stress is decreased by 12 %-15 %. The bottom solution in Table 3 is chosen to be manufactured in consideration of engineering requirements finally.
Fig. 5Sensitivity of each parameter
5. Conclusions
This paper focuses on the fundamental frequency and maximum stress of carbon fiber collapsible hinge based on the modal analysis and quasi-static folding analysis. The results are obtained from experiments and finite element model calculations through ABAQUS. The fundamental frequency and maximum stress are optimized with respect to the hinge size based on surrogate model and optimization algorithm through ISIGHT. The fundamental frequency is increased by 12 %, while the maximum stress is decreased by 13 % after optimal design.
References
-
Wu C., Viquerat A. Natural frequency optimization of braided bistable carbon/epoxy tubes: Analysis of braid angles and stacking sequences. Composite Structures, Vol. 159, 2017, p. 528-537.
-
Wu C., Viquerat A. Natural frequency optimization and stability analysis of bistable carbon fiber reinforced plastic booms for space applications. 3rd AIAA Spacecraft Structures Conference, California, 2016.
-
Piovesan D., Zaccariotto M., Bettanini C. Design and validation of a carbon-fiber collapsible hinge for space applications: a deployable boom. Journal of Mechanisms and Robotics, Vol. 8, Issue 3, 2016, p. 031007.
-
Hu H. T., Tsai J. Y. Maximization of the fundamental frequencies of laminated cylindrical shells with respect to fiber orientations. Journal of Sound and Vibration, Vol. 225, Issue 4, 1999, p. 723-740.
-
Dong S. B. Free vibration of laminated orthotropic cylindrical shells. Journal of the Acoustical Society of America, Vol. 44, Issue 6, 1968, p. 1628-1635.
-
Qatu M. S., Leissa A. W. Natural frequencies for cantilevered doubly-curved laminated composite shallow shells. Composite Structures, Vol. 17, Issue 3, 1991, p. 227-255.
-
Lopatin A. V., Morozov E. V. Fundamental frequency of the laminated composite cylindrical shell with clamped edges. International Journal of Mechanical Sciences, Vol. 92, 2015, p. 35-43.
-
Koide R. M., Luersen M. A. Maximization of fundamental frequency of laminated composite cylindrical shells by ant colony algorithm. Journal of Aerospace Technology and Management, Vol. 5, Issue 1, 2013, p. 75-82.
-
Abouhamze M., Shakeri M. Multi-objective stacking sequence optimization of laminated cylindrical panels using a genetic algorithm and neural networks. Composite Structures, Vol. 81, Issue 2, 2007, p. 253-263.
-
Topal U. Multiobjective optimization of laminated composite cylindrical shells for maximum frequency and bucking load. Materials and Design, Vol. 30, Issue 7, 2009, p. 2584-2594.
-
Mallikarachchi H. M. Y. C., Pellegrino S. Quasi-static folding and deployment of ultrathin composite tape-spring hinges. Journal of Spacecraft and Rockets, Vol. 48, Issue 1, 2011, p. 187-198.
