Comparison of natural frequencies of isotropic plate using DSM with Wittrick-Williams algorithm

Chauhan, Manish; Ranjan, Vinayak; Singh, Baij Nath

doi:10.21595/vp.2018.20401

Vibroengineering Procedia

Browse Procedia

Published: 13 December 2018

Check for updates

Comparison of natural frequencies of isotropic plate using DSM with Wittrick-Williams algorithm

Manish Chauhan¹

Vinayak Ranjan²

Baij Nath Singh³

^{1, 2, 3}Bennett University, Greater Noida, India

³Indian Institute of Technology (IIT-ISM), Dhanbad, India

Corresponding Author:

Manish Chauhan

Cite the article Download PDF

Downloads 1739

CrossRef Citations 1

Abstract

In this paper, comparison of natural undamped frequencies of isotropic plates are investigated by using the dynamics stiffness element for isotropic plates. The DS Matrix for isotropic has been formulated by the application of classical plate theory. The generalized DS matrix has to solve by using Wittrick-Williams algorithm. Results of different aspect ratio have been validated from the existing literature.

1. Introduction

Pure metals have limited applicability in engineering applications because of the requirement of the inconsistent property of materials. In engineering, materials may be required to be hard as well as ductile. To solve this requirement, there is no such material that exists in nature. The combination of one metal (in molten state) with another parent metal or non-metals is required to solve the engineering problem [1]. Another advanced material which is formed by the combination of one or more than one material with different physical and chemical properties in solid states are called composite material The properties of the composite material are better than the individual parent materials [2]. In this article, we study the comparison of the natural frequency of isotropic plate using DSM and FEM. DSM provides very accurate results without depending on the number of elements in the nodal analysis and it is another effective method to the FEM [3]. Boscolo and Banerjee [4] studied about the free vibration analysis of homogeneous isotropic plates. In this paper, we present the comparison of nondimensional natural frequency of plate using DSM from the literature survey. We have used CPT on DSM formulation to derive the dynamic stiffness matrix. Wittrick-Williams algorithm [5] has to solve the transcendental nature of element with find out the nondimensional frequencies of the structure. We show that the natural frequencies are more accurate than available literature and set a standard value for comparison purpose.

2. Theory

2.1. Model development for functionally graded plates

The isotropic plate system has taken in this paper consist of the flexible square plate has different boundary condition at all edges, which are not movable in the neutral surface. CPT and Wittrick-Williams algorithm is described as the displacement field of plate surfaces are brief summaries below.

The Cartesian coordinate system ( $x$ , $y$ , $z$ ), of the isotropic plate, is fixed as represented in Fig. 1 plate’s thickness is $h$ . We assumed that the harmonic distributed force per unit area, $f_{1} \cos (ω t$ ) in the $z$ direction. $u_{o}$ ( $x$ , $y$ , $z$ ), $v_{o}$ ( $x$ , $y$ , $z$ ), and $w_{o}$ ( $x$ , $y$ , $z$ ) are the displacement component of an arbitrary point of the plane of the plate in $x$ , $y$ , and $z$ direction, respectively.

Fig. 1Cartesian coordinate of displacement field of a isotropic plate

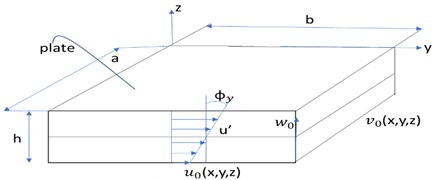
2.2. Classical plate theory (CPT)

The displacement component of an isotropic plate is $u_{o}$ ( $x$ , $y$ , $z$ ), $v_{o}$ ( $x$ , $y$ , $z$ ), and $w_{o}$ ( $x$ , $y$ , $z$ ) by using classical plate theory, shown in Fig. 1, are given by [4]:

1

u_{o} (x, y, z) = u^{'} (x, y) - z \frac{\partial w^{'}}{\partial x}, v_{o} (x, y, z) = v^{'} (x, y) - z \frac{\partial w^{'}}{\partial y}, w_{o} (x, y, z) = w^{'} (x, y) .

In the above expression, the index ( $'$ ) consider the displacement component of the plate geometric. The mid-surface displacement, $u_{o} (x, y)$ and $v_{o} (x, y)$ of a thin homogenous isotropic place can be neglected. The only unknown in the transverse displacement $w_{o}$ is considered in Eq. (1).

Hamilton’s principle has to investigate the nondimensional natural frequency of isotopic plate using the fourth order differential equation of a plate with different boundary conditions:

2

D_{e f f} (\frac{\partial^{4} w^{'}}{\partial x^{4}} + 2 \frac{\partial^{4} w^{'}}{\partial x^{2} \partial y^{2}} + \frac{\partial^{4} w^{'}}{\partial y^{4}}) + ρ h \frac{\partial^{4} w^{'}}{\partial t^{4}} = 0 .

The BCs $a r e^{1}$ :

3

V_{x} : - D_{e f f} (\frac{\partial^{3} w^{'}}{\partial x^{3}} + (2 - υ) \frac{\partial^{3} w^{'}}{\partial x \partial y^{2}}) δ w^{'}, M_{x x} : - D_{e f f} (\frac{\partial^{2} w^{'}}{\partial x^{2}} + υ \frac{\partial^{2} w^{'}}{\partial y^{2}}) δ \emptyset_{y},

where $D_{e f f} = ϵ h^{3} / \{12 (1 - υ^{2})\}$ is the flexural stiffness, $ϵ$ is the property of the material called Young’s modulus, $h$ the plate thickness, and $ρ$ is the density of the material.

2.3. DSM formulation

For DSM formulation the first basic concept is to solve the fourth order differential Eq. (2) of the Isotropic plate. The levy-type [6] boundary condition for exact solution is sought. An isotropic plate has given as simply supported (SS) on two sides and remaining sides can be fixed (F) or clamped (C) The basic formulation of the Eq. (2) which satisfied the boundary condition in following form:

4

w^{'} (x, y, t) = \sum_{m = 1}^{\infty} W_{m} (x) e^{i ω t} \sin (\propto_{m} y), \propto_{m} = \frac{m π}{L}, m = 1,2,

where $ω$ is the unknow frequency. The fourth order ordinary differential equation is to be obtained by substituting Eq. (4) into Eq. (2) as follows:

5

\frac{d^{4} W_{m}}{d x^{4}} - 2 \propto_{m}^{2} \frac{d^{2} W_{m}}{d x^{2}} + (\propto_{m}^{4} - \frac{ρ h ω^{2}}{D_{e f f}}) W_{m} = 0, m = 1,2, \dots, \infty .

The solution of the above quadratic equation determined by applying a trail solution [4]. For solving the differential equation, the two solutions are possible which is to rely depend on the roots:

• Condition 1: $\propto_{m}^{2} \geq ω \sqrt{\frac{I_{0}}{D_{e f f}}} \Rightarrow$ all roots are real ( $\propto_{1 m}, - \propto_{1 m}, \propto_{2 m}, - \propto_{2 m}$ ):

6

\propto_{1 m} = \sqrt{\propto_{m}^{2} + ω \sqrt{\frac{I_{0}}{D_{e f f}}}}, \propto_{2 m} = \sqrt{\propto_{m}^{2} - ω \sqrt{\frac{I_{0}}{D_{e f f}}}} .

The solution is:

7

W_{m} (x) = A_{m} \cosh (\propto_{1 m} x) + B_{m} \sinh (\propto_{1 m} x) + C_{m} \cosh (\propto_{2 m} x) + D_{m} \sinh (\propto_{2 m} x) .

• Condition 2: $\propto_{m}^{2} < ω \sqrt{\frac{I_{0}}{D_{e f f}}} \Rightarrow$ different roots are ( $\propto_{1 m}, - \propto_{1 m}, i \propto_{2 m}, - {i \propto}_{2 m}$ ):

\propto_{1 m} = \sqrt{\propto_{m}^{2} + ω \sqrt{\frac{I_{0}}{D_{e f f}}}}, \propto_{2 m} = \sqrt{- \propto_{m}^{2} + ω \sqrt{\frac{I_{0}}{D_{e f f}}}} .

The solution is:

8

W_{m} (x) = A_{m} \cosh (\propto_{1 m} x) + B_{m} \sinh (\propto_{1 m} x) - C_{m} \cosh (\propto_{2 m} x) + D_{m} \sinh (\propto_{2 m} x) .

Method to solve DS matrix for case 1 is explain below and similarly to solve in second case but is not show for brevity.

In (Eqs. (6) and (4)), the known displacement, the rotation $φ_{y}$ , moment $M_{x x}$ and shear force $V_{x}$ explain in the following form Eq. (3):

9

ϕ_{y m} (x, y) = ϕ_{y m} (x) \sin {(\propto}_{m} y) = - (A_{m} \propto_{1 m} \sinh (\propto_{1 m} x)

+ B_{m} \propto_{1 m} \cosh (\propto_{1 m} x) - C_{m} \propto_{2 m} \sinh (\propto_{2 m} x) + D_{m} \propto_{2 m} \cosh (\propto_{2 m} x)) \sin {(\propto}_{m} y),

10

V_{x m} (x, y) = V_{x m} (x) \sin {(\propto}_{m} y) = D_{e f f} ((A_{m} ({\propto_{1 m}}^{3} - (2 - υ) \propto_{m}^{2} \propto_{1 m} \sinh (\propto_{1 m} x)

{+ B}_{m} ({\propto_{1 m}}^{3} - (2 - υ) \propto_{m}^{2} \propto_{1 m} \cosh (\propto_{1 m} x)

+ C_{m} {(\propto_{2 m}}^{3} - (2 - υ) \propto_{m}^{2} \propto_{2 m} \sinh (\propto_{2 m} x)

{+ D}_{m} {(\propto_{2 m}}^{3} (2 - υ) \propto_{m}^{2} \propto_{2 m}) \cosh (\propto_{2 m} x)) \sin {(\propto}_{m} y)

11

M_{x x m} (x, y) = M_{x x m} (x) \sin {(\propto}_{m} y) = - D_{e f f} (A_{m} ({\propto_{1 m}}^{2} - υ \propto_{m}^{2}) \cosh (\propto_{1 m} x) + B_{m} ({\propto_{1 m}}^{2} - υ \propto_{m}^{2})) \sinh (\propto_{1 m} x)

+ C_{m} ({\propto_{2 m}}^{2} + υ \propto_{m}^{2})) \cos (\propto_{2 m} x) - D_{m} ({\propto_{2 m}}^{2} υ \propto_{m}^{2}) \sin (\propto_{2 m} x)) \sin {(\propto}_{m} y) .

The displacements boundary condition for the plate are:

12

x = 0, W_{m} = W_{1}, ϕ_{y m} = ϕ_{y 1},

x = b, W_{m} = W_{2}, ϕ_{y m} = ϕ_{y 2} .

Similarly, the boundary condition for the forces are:

13

x = 0, V_{x m} = {- V}_{1}, M_{x x m} = {- M}_{1},

x = b, V_{x m} = {- V}_{2}, M_{x x m} = M_{2} .

From Fig. 2, we are implementing the different BCs, i.e. putting Eq. (12) in to Eqs. (6) and (9), the following expression is forming:

14

[\begin{matrix} W_{1} \\ ϕ_{y 1} \\ W_{2} \\ ϕ_{y 1} \end{matrix}] = [\begin{matrix} 1 & 0 & 1 & 0 \\ 0 & - \propto_{1 m} & 0 & - \propto_{2 m} \\ C_{h 1} & S_{h 1} & C_{h 2} & S_{h 2} \\ {- \propto_{1 m} S}_{h 1} & {- \propto_{1 m} C}_{h 1} & {- \propto_{1 m} S}_{h 2} & {- \propto_{1 m} C}_{h 1} \end{matrix}] [\begin{matrix} A_{m} \\ B_{m} \\ C_{m} \\ D_{m} \end{matrix}],

i.e.:

15

δ = A C,

where:

16

C_{h 1} = \cosh {(\propto}_{i m} b), S_{h 1} = \sinh {(\propto}_{i m} b),

C_{i} = \cos {(\propto}_{i m} b), S_{i} = \sin {(\propto}_{i m} b), i = 1,2 .

The BCs for forces, i.e. putting in Eq. (13) into Eqs. (10) and (11), the following matrix has formed:

17

[\begin{matrix} V_{1} \\ M_{1} \\ V_{2} \\ M_{2} \end{matrix}] = [\begin{matrix} 0 & R_{1} & 0 & R_{2} \\ L_{1} & 0 & L_{1} & 0 \\ - R_{1} S_{h 1} & - R_{1} C_{h 1} & - R_{1} S_{h 2} & - R_{1} C_{h 2} \\ - L_{1} C_{h 1} & - L_{1} S_{h 1} & - L_{2} C_{h 1} & - L_{2} S_{h 2} \end{matrix}] [\begin{matrix} A_{m} \\ B_{m} \\ C_{m} \\ D_{m} \end{matrix}],

i.e.:

18

F = R C,

where:

19

R_{i} = D_{e f f} ({\propto_{i m}}^{3} - \propto^{2} \propto_{i m} (2 - ν)), L_{i} = D_{e f f} ({\propto_{i m}}^{2} - \propto^{2} ν),

where $i =$ 1, 2.

From Eqs. (15) and (18) the DS matrix $K$ for the isotropic plate can be obtained and BE leave out the constant factor $C$ to get:

20

F = K δ,

where:

21

K = R A^{- 1} .

From the general expression Eq. (21) to form DS matrix which is similar to six variable terms $s_{v v}$ , $s_{v m}$ , $s_{m m}$ , $f_{v v}$ , $f_{v m}$ , $f_{m m}$ this variable terms describe the effect on shear and moment reason of displacement put on the “same” (s) nodal line, and the “far” nodal line. Thus, the dynamic stiffness matrix ( $K$ ) expressed in following way:

22

K = [\begin{matrix} s_{v v} & s_{v m} & f_{v v} & f_{v m} \\ s_{m m} & {- f}_{v m} & f_{m m} \\ S y m & s_{v v} & {- s}_{v m} \\ s_{m m} \end{matrix}] .

2.4. Algorithm used for the DSM element

The global DS matrix for natural frequency of plate is to obtain by using Wittrick-Williams algorithm [5]. Due to nonlinear behavior of dynamic stiffness element, to drive frequency determinant is excessive difficult. Wittrick and Williams algorithm [5] must be used to solving this problem and ensures that there are no frequencies missed out of the structure:

23

ϖ = ω a^{2} \sqrt{\frac{ρ_{c} h}{D_{c}}} .

3. Numerical results

The numerical results of the DSM formulation have been inserted in a MATLAB and to find the frequencies and mode shape of the structure. This part is to analysis the natural frequencies of the isotropic plate by using DSM with CPT based on Levi-type BCs to the available literature Leissa [7] values.

The natural frequencies of simple supported (SS) isotropic plates are shown in Table 1, and Table 2. The four different edge boundary condition are applying as notification SS-F-SS C.

Table 1Non-dimensional natural frequencies (ϖ=ωa2 ρch/Dc for SS-F-SS-F plate

S-F-S-F	$a / b$	$ν =$ 0		$ν =$ 0.3		$ν =$ 0.5
$m n$	0.4	Present	Ref [10]	Present	Ref [10]	Present	Ref [10]
1 1		9.8696	9.8696	9.7600	9·7600	9.4506	9·4506
2 1		39.4784	39.4784	39.2386	39.2387	38.3771	38.3771
1 1	1	9.8696	9.8696	9.6313	9.6314	9.0792	9.0793
2 1		39.4784	39.4787	38.9449	38.9450	37.5191	37.5192
3 1		88.8264	88.8264	87.9866	87.9867	85.4898	85.4899
1 1	2.5	9.8696	9.8696	9.4841	9.4841	8.7042	8.7042
2 1		39.4784	39.4787	38.3629	38.3629	35.8798	35.8799
3 1		88.8264	88.8264	86.9684	86.9684	82.5093	82.5093
4 1		157.9136	157.9137	155.3211	155.3211	148.725	148.7256

Table 2Non-dimensional natural frequencies (ϖ=ωa2 ρch/Dc for SS-SS-SS-SS isotropic square plate

S-S-S-S
$m n$	Present	Ref [8]	Ref [9]	Ref [10]
1 1	19.7392	19.7392	19.739	19.739
1 2	49.3480	49.3490	49.348	49.348
2 1	49.3480	49.3490	49.348	49.348
2 2	78.9568	79.4007	78.957	78.957
1 3	98.6960	100.1729	99.304	100.17
3 1	98.6960	100.1868	99.304	–
3 2	128.3048	130.3895	–	–

4. Conclusions

Present work is used to understand the vibration analysis of isotropic plate was studied using classical plate theory under different levy type boundary conditions. This present study to solve the natural frequencies of plate by formulating the dynamic stiffness matrix together with CPT. Wittrick-William algorithm to take into account the nonlinear behaviour of the DSM element. Formulation is used to solve the dynamics stiffness matrix with applying boundary condition has been import in MATLAB and extract the nondimensional frequencies of plate beside a high degree of desired accuracy. Thus, the result has been investigated to the acceptable comparison of natural frequencies of isotropic plate.

References

Wikipedia, http://en.wikipedia.org/wiki/Alloy.

Search CrossRef
Hon D., Shiraishi N. Wood and Cellulose Chemistry. 2nd Edition, Marcel Dekker, New York, 2001.

Search CrossRef
Leung A. Y. T. Dynamic Stiffness and Substructures. Springer Science and Business, 1993.

Publisher
Boscolo M., Banerjee J. R. Dynamic stiffness method for exact in plane free vibration analysis of plates and plate assemblies. Journal of Sound and Vibration, Vol. 330, Issue 12, 2011, p. 2928-2936.

Publisher
Wittrick W. H., Williams F. W. Buckling and vibration of anisotropic or isotropic plate assemblies under combined loadings. International Journal of Mechanical Sciences, Vol. 16, Issue 4, 1974, p. 209-239.

Publisher
Ince E. L. Ordinary Differential Equations. Dover Publications, 1920.

Search CrossRef
Leissa A. W. The free vibration of rectangular plates. Journal of Sound and Vibration, Vol. 31, Issue 3, 1973, p. 257-293.

Publisher
Chakraverty S., Pradhan K. K. Free vibration of functionally graded thin rectangular plates resting on Winkler elastic foundation with general boundary conditions using Rayleigh-Ritz method. International Journal of Applied Mechanics, Vol. 6, Issue 4, 2014, p. 1450043.

Publisher
Bhat R. B. Natural frequencies of rectangular plates using characteristic orthogonal polynomials in Rayleigh-Ritz method. Journal of Sound and Vibration, Vol. 102, Issue 4, 1985, p. 493-499.

Publisher
Singh B., Chakraverty S. Flexural vibration of skew plates using boundary characteristic orthogonal polynomials in two variables. Journal of Sound and Vibration, Vol. 173, Issue 2, 1994, p. 157-178.

Publisher

Cited by

Dynamic stiffness method for free vibration analysis of thin functionally graded rectangular plates

Manish Chauhan | Vinayak Ranjan | Prabhakar Sathujoda

(2019)

About this article

Received

19 November 2018

Accepted

26 November 2018

Published

13 December 2018

SUBJECTS

Modal analysis and applications

DOI

https://doi.org/10.21595/vp.2018.20401

Keywords

dynamic stiffness matrix

isotropic plate

classical plate theory

Wittrick-Williams algorithm

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2019 11 28

Dynamic stiffness method for free vibration analysis of thin functionally graded rectangular plates

Manish Chauhan, Vinayak Ranjan, Prabhakar Sathujoda

Research article

2019 11 28

Free vibration of circular annular plate with different boundary conditions

Yash Jaiman, Baij Singh

Research article

2019 05 15

Free vibration of a Levy-type solution for plates based on two-variable refined plate theory by using SEM

Shota Kiryu, Sofia W. Alisjahbana, Irene Alisjahbana, Mitsuo Nagao, Buntara S. Gan

Research article

2018 12 13

Analysis of free vibration of nano plate resting on Winkler foundation

Piyush Pratap Singh, Mohammad Sikandar Azam, Vinayak Ranjan

M. Chauhan, V. Ranjan, and B. N. Singh, “Comparison of natural frequencies of isotropic plate using DSM with Wittrick-Williams algorithm,” Vibroengineering PROCEDIA, Vol. 21, pp. 59–64, Dec. 2018, https://doi.org/10.21595/vp.2018.20401

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2018.20401
UR  - https://doi.org/10.21595/vp.2018.20401
TI  - Comparison of natural frequencies of isotropic plate using DSM with Wittrick-Williams algorithm
T2  - Vibroengineering PROCEDIA
AU  - Chauhan, Manish
AU  - Ranjan, Vinayak
AU  - Singh, Baij Nath
PY  - 2018
DA  - 2018/12/13
PB  - JVE International Ltd.
SP  - 59-64
VL  - 21
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Chauhan_2018,
	doi = {10.21595/vp.2018.20401},
	url = {https://doi.org/10.21595/vp.2018.20401},
	year = 2018,
	month = {dec},
	publisher = {{JVE} International Ltd.},
	volume = {21},
	pages = {59--64},
	author = {Manish Chauhan and Vinayak Ranjan and Baij Nath Singh},
	title = {Comparison of natural frequencies of isotropic plate using {DSM} with Wittrick-Williams algorithm},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]M. Chauhan, V. Ranjan, and B. N. Singh, “Comparison of natural frequencies of isotropic plate using DSM with Wittrick-Williams algorithm,” Vibroengineering PROCEDIA, vol. 21, pp. 59–64, Dec. 2018, doi: 10.21595/vp.2018.20401.

Copy IEEE

Copied to clipboard!

Chauhan, Manish, Vinayak Ranjan, and Baij Nath Singh. “Comparison of Natural Frequencies of Isotropic Plate Using DSM with Wittrick-Williams Algorithm.” Vibroengineering PROCEDIA 21 (December 13, 2018): 59–64. https://doi.org/10.21595/vp.2018.20401.

Copy Chicago

Copied to clipboard!

Comparison of natural frequencies of isotropic plate using DSM with Wittrick-Williams algorithm

Abstract

1. Introduction

2. Theory

2.1. Model development for functionally graded plates

2.2. Classical plate theory (CPT)

2.3. DSM formulation

2.4. Algorithm used for the DSM element

3. Numerical results

4. Conclusions

References

Cited by

About this article

Related Articles