Analysis of free vibration of nano plate resting on Winkler foundation

1. Introduction

Nanoplates are the building blocks for various nanoscale objects which are called nanostructures. Recent, development of nanotechnology enables new generation devices with enhanced functionality hence playing vital roles in many engineering fields. These materials have superior properties as compared to conventional materials [1].

In recent time the nanomaterials have become the important components of different modern nanoelectromechanical systems [2]. It is thus necessary to analyse vibration behaviour in order to design nanostructures. Experimental analysis at nanoscale size is tough to carry out, hence efficient mathematical models for nanostructures analysis is needed. Vibration analysis of Nanostructures with traditional models shows that properties changes to an extent at nanoscale called size effect. When the system is reduced to nanoscale it can no longer be modelled as a continuum as systems become comparable to intermolecular spacing. If small-scale effects in Nano designing are ignored then this may lead to faulty Nano system design. Hence in order to achieve an accurate solution for correct and realistic design small scale effects must be taken into account. In order to overcome these shortcommings different continuum models as couple stress theory [3], modified couple stress theory [4], strain gradient theory [5] and nonlocal elasticity theory [6] were given. Among these thories, the nonlocal elasticity theory proposed by Eringen is mostly considered. Nonlocal Continuum mechanics theory put forward by Eringen [7] incorporates small length scale effect which plays a key role when Nano structures are taken into account. This theory is a widely used as results are found to be an accurate and quick analysis of Nano plates can be done. According to the nonlocal elasticity theory, the stress at a specific point not only depends on stress at that point but also the stresses of every points of that body. In the present work, governing equations of classical plate theory is based on nonlocal elasticity theory. Natrajan et al. [8] analysed the size effect on linear free vibration behaviour of nano plate using Erigen’s nonlocal elasticity theory. Murmu and Pradhan [9] analysed the scaling effect on vibration behaviour of nano plate using nonlocal continuum mechanics. Behra et al. [10] studied the vibration of the rectangular isotropic nano plate. Daneshmehr et al. [11] studied the vibration of functionally graded nano plate with the help of non-local theory. Hence it is can be seen that Erigen non-local theory is widely used to analyse the vibration behaviour of different nano plate structures.

Previous literature suggests that most of the studies focuses analysis of vibration behaviour of nano beams and nano plates of isotropic material plates without any interaction with foundation. Very less study is found to be conducted on analysis of plate on foundation. In number of applications Nano plates on elastic foundation, are used. Different elastic medium models for analysis of plate on elastic foundation were proposed by number of researchers. One of the reported models is Winkler model [12], which is derived from Winkler's hypotheses. This model considers vertical closely spaced linear springs as the elastic medium. This model is considered as building block and is easy to solve.

According to literature many authors have tried to solve the problem using a different method as Finite Element Method, Differential quadrature methods etc. It is to be noted that when the plate is rested on elastic foundation then these methods become very difficult to solve and accurate result cannot be obtained. It can be concluded that previous methods are not efficient for analysis of plate resting on Winkler foundation. In present article, authors have obtained the accurate solution of natural frequency with help of Kirchoff’s theory and Rayleigh Ritz method. Few studies have used this method for the analysis of large scale plate [13]. The extant literature review suggests that no study highlights in detail, the effect of various material and foundation parameters on Nano plates resting on elastic support subjected to different combinations of boundary conditions.

2. Mathematical modelling

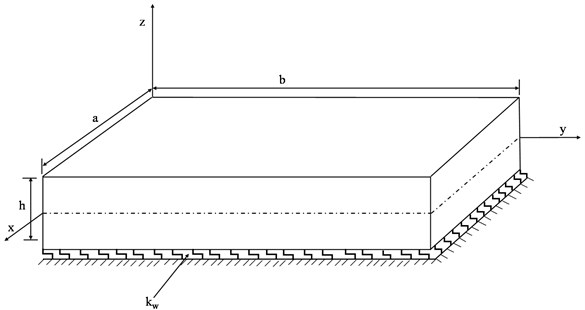
Nano plate of dimension $a$×$b$ as shown in Fig. 1, has been considered for analysis. The edges are taken along the $x$, $y$ axes for the mathematical modelling of the Nano plate that rest on Winkler foundation. The $z$-axis is considered perpendicular to $xy$ – plane.

Fig. 1Winkler foundation supporting nano plate

According to classical plate theory, displacements of a point is expressed by equation:

where, $u$, $v$ and $w$ denote displacement in the $x$, $y$ and $z$ axes and $w$ represents a deflection along the $z$-axis. Neglecting the transverse shear caused due to in-plane stretching and bending, the linear strain linked with the displacement field is:

Strain energy of an elastic Nano plate is formulated as:

The effective strain energy ($U_{eff}=U+U_{foundation}$) of the nano plate, on Winkler-Pasternak elastic foundation, is:

where, $\mu ={\left(c_0{l}_{\mathrm{i}\mathrm{n}\mathrm{t}}\right)}^2$ [6] is the nonlocal parameter, $l_{int}$ denotes internal characteristic length, $c_0$ represents constant and $k_w$ shows stiffness of Winkler foundation. The kinetic energy of the nano plate on Winkler foundation in simplified form is given by:

where, $m_0$ is $\rho h$.

The harmonic type displacement components are assumed as:

where, $w\left(x,y,t\right)$, $W(x,y)$ and $\omega$ are transverse deflection, maximum deflection and frequency of free vibration of the nano plate on elastic foundation.

Now, on equating the maximum strain energy $U_{ef{f}_{\mathrm{m}\mathrm{a}\mathrm{x}}}$ and kinetic energy $T_{\mathrm{m}\mathrm{a}\mathrm{x}}$ we will get Rayleigh quotient, given by the following equations:

The maximum deflection $W(x,y)$ is the summation of the series of simple algebraic polynomials involving $x$ and $y$, presented as:

where, $c_i$ are unknown constants and $f_i$ are function generated. The functions ($f_i$) contain polynomials $\varphi$ and simple polynomials $g_i(x,y)$ are represented as:

where exponents $p$, $q$, $r$ and $s$ stands for edge conditions of different edges.

Moreover, considering the partial derivative of ${\omega }^2$ w.r.t unknown constant and then equating it with zero, gives:

Further simplifying the Eq. (15), we get the following equation in term of Stiffness and inertia matrix:

where:

$\lambda$ is the nondimensionalised frequency parameter, and $K$, $K_{foundation}$ and $M$ are stiffness and mass matrices respectively.

3. Results and discussions

3.1. Convergence and validation

The frequency parameter of nano plates is analysed in detail in this section. Convergence test is carried assure the accuracy of present result. Authors further compared the obtained results with the results available in the literature. For test of convergence and comparison, the nano plate is considered to be under SSSS edge condition without foundation.

3.1.1. Convergence

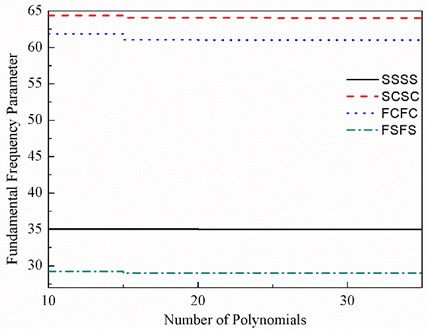
Convergence of frequency parameter of nano plate subjected to various boundary conditions is shown in Fig. 2 with respect to different number of the polynomials. The figure suggests that the frequency parameter converges with increase in the number of polynomials, to the exact frequency and becomes constant after certain no. of polynomial i.e. 40 in present case.

Fig. 2Convergence of fundamental frequency parameter of nano plate

3.1.2. Comparison

The non-dimensional natural frequency is compared with Aghababei and Reddy as reported in Table 1. An excellent agreement between the results can be observed.

Table 1Comparison of frequency parameter (λm×n=ωm×nhρ/G) of SSSS (simply supported) square plate. (E= 30×106, ν= 0.3)

Frequencies	$\mu$	Aghababei and Reddy [14]	Present
${\lambda }_{1\times 1}$	0	0.0963	0.09636
	1	0.0880	0.0880
${\lambda }_{2\times 2}$	0	0.3853	0.3874
	1	0.288	0.2884
${\lambda }_{3\times 3}$	0	0.8669	0.8608
	1	0.5202	0.51671

4. Conclusions

The authors used the classical plate theory along with Eringen’s nonlocal elasticity theory to analyse the frequency parameter of nano plate under different combination of boundary condition that rest on Winkler elastic foundation. Effect of the aspect ratio, stiffness of Winkler foundation and nonlocal parameter on the vibration behaviour of nano plate is studied. It can be concluded from the results that non-local parameter has an influence on vibration behaviour of small scale plate for all considered BCs hence it should always be considered for modelling small scale plate structure. Further study reveals that frequency parameters increases on increasing aspect ratio for every BCs. It is also concluded that the effect of stiffness of Winkler foundation on vibration behaviour of nano plate is insignificant.