The vibration analysis of a nanobeam due to a ramp-type heating under Moore-Gibson-Thompson theory of thermoelasticity

1. Introduction

Nanomechanical resonators have been of great significance. For instance, in communications systems and mechanical electrometers or magnetometers, resonators made of silicone crystal material typically with semi-conductive techniques for the development of MHz or even GHz core frequencies may be used for the identification, force, pressure or acceleration sensitive loads [1-3]. Researchers are interested in understanding how the physical and mechanical properties of resonant parameters affect them. Sun et al. [4] test thermoelastic damping (TED) in the microbeam resonators based on generalized thermoelasticity theory with one relaxation time of Lord and Shulman (LS) model [5]. To solve combined thermoelastic equations, he used finite Fourier sinus transformation methods and Laplace methods, which extracted the expressions of fluidity and heat. The deflect vibrates in a simulated state mode when the thermal moment vibrates in the same mode as the deflection at first. In the form of the updated theory of couple tension, Hosseini [6] studied TED and microbeam resonator dynamical behaviour using the theory of thermoelasticity. For the solution of thermoelastic variations and the representation of the beam deflection and thermoelectric moment, the Laplace Transformation technology was adopted. However, the results of the modified pair stress theory on deflection and thermal moment are not evident in their work.

Kumar recently investigated and expanded on the role of the Sun and its impacts on deflection and thermal moment in microbeam resonators, taking into consideration the three-phase of thermoelasticity phase-lags ideas (TPL) [7]. We also address several experiments on thermoelastic beam vibration, as references in the literature indicate [8-13].

Given the foregoing description of beam resonator thermomechanical testing, this study intends to investigate the thermal and dynamic behaviour of simply by using MGT thermoelasticity theory, as recently mentioned by Quintanilla [14]; this is the Moore-Gibson-Thompson (MGT) equation. In this paper, the heat conduction equation is described. In reality, this modified heat conduction equation is reached when the relaxation parameter is implemented in the Green-Naghdi type-III model (GN-III) [15, 16]. The coupled thermoelastic problem's governing equations are derived based on the MGT, LS, and GN-III models [16]. Through comparing the findings achieved under the MGT model with those of LS and GN-III models, vibration responses of the deflection and the thermal time are analyzed [16].

In the current work, ramp-type heating as a thermal loading will be applied on thermoelastic isotropic nanobeam. A simplified form of thermoelasticity theory will be used for Moore-Gibson-Thompson. The transform technique for Laplace will be used and its inversions will be computed using the approximation numerical Tzou procedure. The numerical results for a rectangular nanobeam made of silicon nitride will be applied to validate the results.

2. Basic equations

A homogeneous thermal isotropic, thermal viscoelastic solid in the Cartesian coordination category Kelvin-Voigt was considered at a uniform temperature $T_0$ and initially undeformed. The fundamental differential motion and heat conduction equations for generalized thermoelasticity are based on the thermal control legislation of Non-Fourier.

Without body forces and heat sources, the displacement components $u_i$ and absolute temperature $T$ are given by [17].

The equations of motion take the form:

The constitutive equations with damage mechanics consideration are in the forms [18]:

The Moore-Gibson-Thompson (MGT) heat conduction equation takes the form [14, 18, 19]:

The MGT theory is the widespread thermoelasticity of the Lord and Shulman theory (LS) and Type-III (GN-III) thermoelasticity of Green-Naghdi [16]. The thermoelastic Eq. (3) therefore gives:

– If $K^{\mathrm{*}}=0$and${\tau }_q\ne 0$, we obtain the Lord-Shulman (LS) model [19].

– If $K^{\mathrm{*}}\ne 0$and${\tau }_q=0$, we obtain the Green-Naghdi (GN-III) model [16, 19].

– If $K^{\mathrm{*}}\ne 0$and${\tau }_q\ne 0$, we obtain the Moore-Gibson-Thompson (MGT) model [14].

The deformation-displacement relations are in the form:

where $i,j=x,y,z$, $\beta =\left(3\lambda +2\mu \right){\alpha }_T$, ${\alpha }_T$ is the coefficient of linear thermal expansion, $\rho$ is the density, ${\tau }_q$ is the thermal relaxation time, $\lambda$, $\mu$ Lamè’s parameter in the usual case, ${\delta }_{ij}$ is the Kronecker delta symbol, $K$ is the thermal conductivity, $K^{\mathrm{*}}$ is the conductivity rate parameter, and $C_{\upsilon }$ is the specific heat at constant strain, and for stable solution $K>K^{\mathrm{*}}{\tau }_q$ [14, 19].

3. Problem formulation

We consider a thin thermoelastic nanobeam of length $\mathcal{l}\mathcal{}$$\left(0\le x\le \mathcal{l}\right)$, width $b$$\left(-b/2\le y\le b/2\right)$, and thickness $h$$\left(-h/2\le z\le h/2\right)$with small flexural deflections. The three axes $x$, $y$, and $z$ are defined along the longitudinal, width, and thickness directions of the beam, respectively.

In the state of equilibrium, the nanobeam is unstrained, unstressed, and without any mechanical damping. Moreover, the reference temperature is $T_0$ everywhere [6].

Fig. 1Rectangular thermoelastic nanobeam

In this work, the well-known Euler-Bernoulli equation [20] is adopted, therefore any plane cross-section that is at first perpendicular to the axis of the beam stays flat and perpendicular during bending to the neutral surface as in Fig. 1.

Hence, the displacement components take the forms:

where $w\left(x,t\right)$ is defined as the lateral deflection.

The flexural moment of the nanobeam cross-section is given by:

where $I=b{h}^3/12$ gives the moment of inertia of the nanobeam cross-section around the $x$-axis and $M_T$ defines the thermal moment of the nanobeam about the $x$-axis, and it is given by:

As a result, the differential equation of thermally induced lateral vibration of the beam may be written as [20]:

where $A=hb$ is the cross-section area.

The non-Fourier heat conduction Eq. (3) takes the form [20]:

where:

is the volumetric strain which gives from Eq. (4) and Eq. (5) that:

The nanobeam has no heat flow across the upper and lower surfaces of the beam, thus, ${\left.\frac{\partial T\left(x,z,t\right)}{\partial z}\right|}_{z=\frac{\pm h}{2}}=0$.

For a very thin nanobeam, we assume the temperature varies in terms of a “$\mathrm{s}\mathrm{i}\mathrm{n}\left(pz\right)$” function through the thickness direction as follows [21]:

where $\theta \left(x,z,t\right)$ is the temperature increment and $p=\pi /h$.

Hence, form Eq. (7), Eq. (8), and Eq. (13), we obtain:

From Eq. (9) and Eq. (13), we get:

where $\epsilon =\rho C_{\upsilon }/K$ and $\delta =K^{\mathrm{*}}/K$.

Thus, we have:

– When $\delta =0$, ${\tau }_q\ne 0$, we obtain the Lord-Shulman (LS) model.

– When $\delta \ne 0$, ${\tau }_q=0$, we receive the Green-Naghdi type-III (GN-III) model.

– When $\delta \ne 0$, ${\tau }_q\ne 0$, we get the Moore–Gibson–Thompson (MGT) model.

Hence, equations and Eq. (14) gives:

After executing the integrations, Eq. (17) takes the form:

In Eq. (15), we multiply both sides by $z$ and integrate for $z$ from $\left(-h/2\right)$ to $\left(h/2\right)$, then we obtain:

For simplicity, the following non-dimensional variables will be applied [19], [22]:

where $c_0^2=\lambda +2\mu /\rho$.

Then, we have the following equations:

where ${\epsilon }_1=\epsilon \mathcal{l}/c_0$, ${\epsilon }_2=\left(3\lambda +2\mu \right){\alpha }_T\mathcal{}\mathcal{l}h{\pi }^2/24c_{0}K$, ${\epsilon }_3=12/h^2$, ${\epsilon }_4=24{\epsilon }_5/h{\pi }^2$, and ${\epsilon }_5=\left(3\lambda +2\mu \right){\alpha }_T{T}_0/\left(\lambda +2\mu \right)$.

(The primes have been cancelled for convenience).

4. Formulation of the problem by using Laplace transform

The Laplace transform will be applied for Eq. (21) and Eq. (22), which is defined by the following formula:

The Laplace transform inversions could be obtained by using the following formula:

where $i$ is an imaginary number unit and $\mathrm{R}\mathrm{e}$ is the real part.

For faster convergence, many numerical experiments have concluded that the value $\kappa$satisfies the relation $\kappa t\approx 4.7$ Tzou [22, 23].

Hence:

where ${\alpha }_1=\left(s^2+{\tau }_q{s}^3\right)/\left(\delta +s\right)$ and ${\alpha }_2=\left(p^2+{\alpha }_1{\epsilon }_1\right)$.

We can re-write Eq. (26) and Eq. (27) to be in the forms:

where $D^r=d^r/d{x}^r$.

After elimination, we get:

where $L=\left({\alpha }_2+{\alpha }_1{\epsilon }_2{\epsilon }_4\right)$, $M={\epsilon }_3{s}^2$, and $N={\epsilon }_3{\alpha }_2{s}^2$.

The general solutions of Eq. (30) and Eq. (31) will take the forms:

where $A_i$, $B_i$, and $C_i$ are unknown parameters to be determined, and the roots of the characteristic equation are $\pm k_1$, $\pm k_2$, and $\pm k_3$ which satisfy the following characteristic equation:

To get the parameters, $C_i$ we will substitute from Eq. (33) and Eq. (34) into the Eq. (30). Hence, we have:

which gives:

To calculate the parameters $A_i$, $i=$ 1, 2, 3, we must use the boundary conditions.

We consider that the first end of the beam $x=0$ is thermally loaded by a function $g\left(t\right)$ and simply supported as follows:

where ${\vartheta }_0$is constant.

The second end of the beam $x=\mathcal{l}$ is simply supported, and zero temperature increment:

Applying the Laplace transform, we get:

Then we obtain the system of linear equations shown below:

A mathematical software MAPLE 2020 has been used to solve the above system and obtain the constants $A_1$, $A_2$, $A_3$.

Hence, we get:

The lateral deflection is:

and the deformation from Eq. (29) and Eq. (50) takes the form:

which complete the solution in the Laplace transform domain.

5. Numerical Results

For the thermal loading, we considered the ramp-type heating, which takes the form [22]:

By applying Laplace transform on the above equation, we get:

Finally, Eq. (49), Eq. (50), Eq. (51), and Eq. (53) represent the solutions in the Laplace transform domain. For the numerical results purpose, the silicon nitride has been taken as the thermoelastic material for which we considered the following values of the different physical constants [17, 20, 24]: $k=$ 43.5 W/(m K), ${\alpha }_T=$ 2.71 10^-6 K^-1, $\rho =$ 3200 kg/m³, $T_0=$ 293 K, $C_{\upsilon }=$ 630 J/(kg K), $\lambda =$217×10⁹ N/m², $\mu =$108×10⁹ N/m², ${\tau }_0=$4.32×10^-13 s.

The aspect ratios of the nanobeam have been fixed as $\mathcal{l}/h=$ 8 and $b=h/2$. For the nanobeam, we will assume the range of the nanobeam length is $\mathcal{l}\left(1-100\right)\times 10^{-12}m$, and the original time $t$ and the relaxation time ${\tau }_q$ are of order 10^-12sec and 10^-14sec, respectively.

The figures will be prepared by using the non-dimensional variables for nanobeam as $\mathcal{l}=$ 0.5, ${\theta }_0=$ 1.0, $z=$$h$/4, and $t=$ 1.0.

6. Discussion

Figs. 2-5 represent the temperature increment, lateral deflection, strain, and stress distributions for the three studied models: Lord-Shulman (LS), Green-Naghdi type-III (GN-III), and the newest one Moore-Gibson-Thompson (MGT) when $t=t_0$.

Fig. 2The temperature increment for different models when t=t0

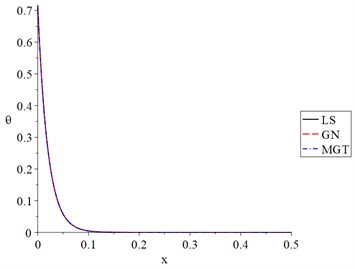
Fig. 3The lateral deflection for different models when t=t0

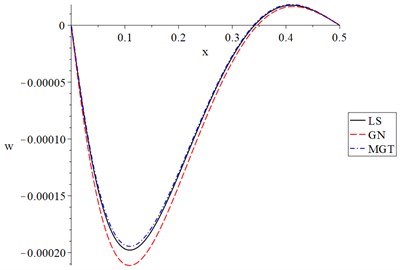
Fig. 2 shows that the three models offer the same behaviour and values for the temperature increment, where the three curves are very close from the beginning up to the end.

Fig. 3 shows that the parameters $\delta$ and ${\tau }_q$ have significant effects on the lateral deflection distributions. The absolute values of the lateral deflection take the following order:

Fig. 4 shows that the parameters $\delta$ and ${\tau }_q$ have significant effects on the strain distributions. The absolute values of the strain take the following order:

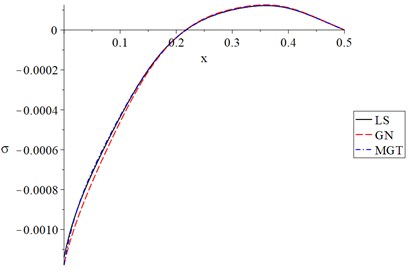
Fig. 5 shows that the parameters $\delta$ and ${\tau }_q$ have significant effects on the stress distributions. The absolute values of the strain take the following order:

Fig. 4The strain for different models when t=t0

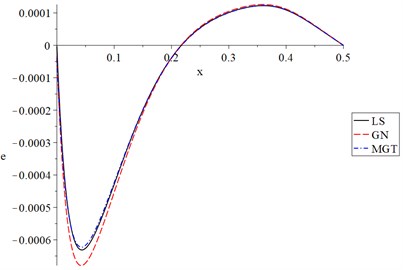
Fig. 5The stress for different models when t=t0

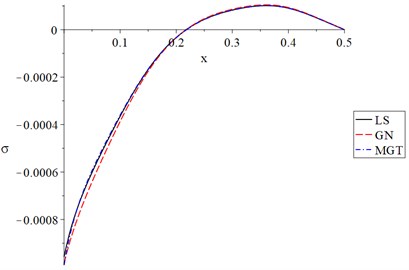
Figs. 6-9 show the temperature increment, lateral deflection, strain, and stress distributions for the three studied models: Lord-Shulman (LS), Green-Naghdi type-III (GN-III), and the newest one Moore-Gibson-Thompson (MGT) when $t<t_0$. Those figures show the same behaviour of the distributions in Figs. 2-5 for the temperature increment, lateral deflection, strain, and stress but with different values due to the ramp-time heat parameter $t_0$.

Fig. 6The temperature increment for different models when t<t0

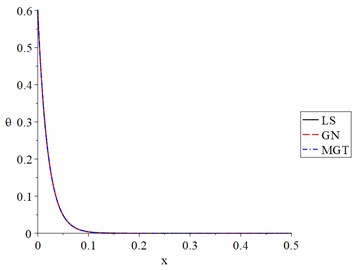
Fig. 7The lateral deflection for different models when t<t0

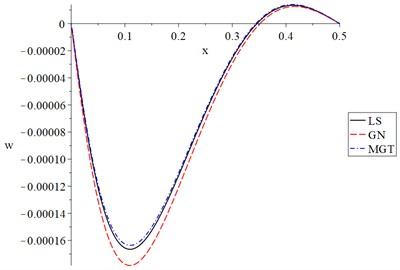
We noted that an increase in the value of the ramp-time heat parameter leads to a decrease in the temperature increment, lateral deflection, strain, and stress of the nanobeam.

Thus, the ramp-time heat parameter $t_0$ has significant effects on all the studied functions and the thermomechanical waves' propagation through the nanobeam.

Fig. 8The strain for different models when t<t0

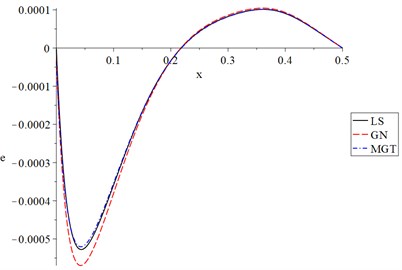
Fig. 9The stress for different models when t<t0

7. Conclusions

The current study looks at the temperature increment, lateral deflection, strain, and stress of a simply supported nanobeam resonator heated using a ramp. In terms of dimensionless temperature increment, lateral deflection, strain, and stress functions, the governing equations for three distinct coupled thermoelasticity theories (LS, GN-III, and MGT) of nanobeams have been developed. The following are the major achievements of this work:

1) The temperature increment under the three studied models is approximately the same.

2) The absolute values of the vibration, strain, and stress in the context of the GN model are greater than its values under the LS model, and they have smaller values under the MGT model.

3) As the uniform load on the upper surface of the nanobeam rises, so do the deflection amplitudes and thermal momentum.

4) As the ramp-time heat parameter is increased, the temperature rise, lateral deflection, strain, and stress decrease.

5) The relaxation parameter has a considerable effect on the vibration of the lateral deflection, strain, and stress distributions.

6) In future work, this work could be extended to include other types of thermal and mechanical loading and different types of nanobeams such as circular nanobeams.