Abstract
A hybrid energy finite element method (Hybrid-EFEM) considering direct field is introduced and promoted to general coupling conditions. The equivalent stress amplitude based on energy density is derived. Then combined with zero order moment stress spectrum method, a high-frequency fatigue life prediction method based on Hybrid-EFEM is proposed. A fatigue life prediction example is carried out to verify the feasibility of the method.
1. Introduction
High-frequency random pressure may cause serious engineering structure fatigue damage [1], so, it is necessary to forecast the fatigue life of the structure under high frequency vibration. The classical frequency-domain fatigue life prediction like Rayleigh approximation [2], Dirlik’s formula [3] methods are based on the stress power spectral density. As such, the outcomes of the traditional high-frequency energy algorithms such as Statistical Energy Analysis (SEA) and EFEM, which refer to the average energy in the frequency band, cannot be applied directly to estimate the fatigue life. Wang et al. [4] researched the influence of the stress power spectral density (PSD) shape on fatigue life estimation. A large number of numerical simulations shows fatigue life is not sensitive to the shape when the zero-order moment of stress PSD remains unchanged. Thus, a Zero Order Moment Stress Spectrum Method is proposed, which only need the stress RMS in the band Compared with the traditional frequency domain method, and the feasibility of the method is verified by a large number of examples.
The zero-order moment of the stress PSD in Y. Y. Wang’s method is calculated by SEA. Since SEA is a statistical averaging method, which can only get the average energy of the substructure, so the maximum stress position on the substructure and its stress level cannot be predicted [5]. Therefore, the predicted life value is so large to bring the risk to the actual structural design. EFEM can overcome the shortcoming of SEA to some extent, but the predict result is still very rough due to many assumptions, one is plane wave assumption [6]. Smith [7] taken the direct circle wave field component into account to solve the high frequency point-loaded plate vibration, and then come up with the Hybrid-EFEM. The accuracy of simulated response near the exciting point has been greatly improved compared with traditional EFEM. P. Hardy [8] considered the energy flow on the boundary, then extended hybrid-EFEM to two board structures, which provides a new idea for the application of Hybrid-EFEM to general coupling conditions.
The bending wave energy accounted for the main role when the plate is under high-frequency transverse excitation. Therefore, this paper only focus on the bending wave, Hybrid-EFEM will be considered to extend to general coupling conditions, then combined with Zero Order Moment Stress Spectrum Method to predict the fatigue life of the actual structure with high frequency random vibration.
2. The theory of Hybrid-EFEM
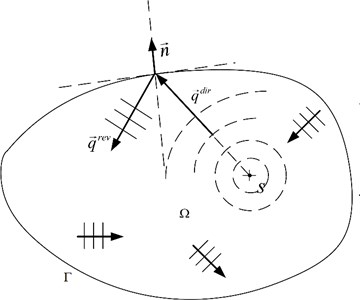
The Hybrid-EFEM considers the energy in the plate to be composed of two parts: The direct field and the reverberant field. The direct field is composed of cylindrical waves coming from external sources. The reverberant field is due to reflection and transmission at subsystem junctions.
2.1. The direct field and reverberant field
Fig. 1 shows the wave field components in a plate: where is the exciting position, and represent direct and reverberant power flow intensity. represent domain, represent boundary.
Fig. 1Wave field components in a plate
The total energy density and power flow intensity in the domain can be written as [7]:
where, the subscript represents the direct field, r represents the reverberant field.
The energy density of the direct field is:
where, represents the distance from the excitation point, and is expressed as .
The reverberant field can be written as [8]:
2.2. Coupling boundary
P. Hardy deduces the bending wave energy flow at the junction of two plates using the energy transfer coefficient and power flow balance [8]. According to P. Hardy’s thought, the Hybrid-EFEM, which only consider the role of bending wave can be extended to general coupling conditions. Considering the space limitations, here we do not present the detailed derivation.
2.3. An example of hybrid-EFEM
Consider the two square plates that are coupled as Fig. 2, and the material parameters and dimensions of the two plates are shown in the Table 1.
Fig. 2L-type coupling plate
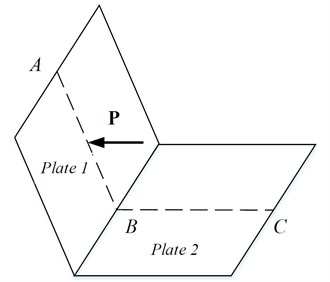
Table 1Size and material parameter
Parameter | Length (m) | Thickness (mm) | Elastic modulus (GPa) | Density (kg/m3) | Poisson |
Plate1 | 1 | 1 | 71 | 2700 | 0.3296 |
Plate2 | 1 | 1 | 21 | 7800 | 0.3125 |
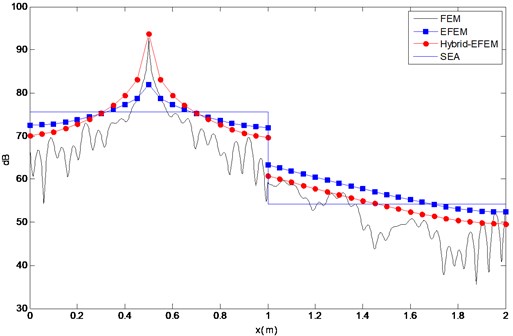
Considering a unit force and 1000 Hz, 0.1. The result on the dotted line calculated by FEM, Hybrid-EFEM, EFEM and SEA is shown in Fig. 3.
It can be seen that compared with EFEM and SEA, Hybrid-EFEM can better simulate the responses especially places near the excitation point. This is of great significance to predict the location and stress level of the structure’s dangerous point.
Fig. 3Comparison of bending energy results in four methods
3. Fatigue life prediction based on the zero order moment stress spectrum method
3.1. Zero order moment stress spectrum theory
Y. Y. Wang [4] analyzes the influence of the stress PSD shape on the fatigue damage and obtains that the fatigue damage is insensitive to the shape of the stress PSD, and only the stress RMS is enough for the fatigue life estimation, as for broad-band processes, the whole band can be divided into several partitions, and the stress RMS of each partition is used to estimate the fatigue damage.
3.2. Application of hybrid-EFEM in zero order moment stress spectrum method
From the Parseval theorem we can see: The zero order moment of a physical quantity’s PSD is equal to the mean square of the physical quantity. Thus, we can use the Hybrid-EFEM to determine the sturacture’s total energy in the 1/3 octave, then, A formulation for estimating the equivalent stress from the energy density is deduced like SEA [5]. Then, the zero order moment of the stress PSD in the octave band is obtained through Parseval theorem. Ultimately, the structural fatigue life prediction is carried out by combining the zero order moment stress spectrum method.
Considering the type of three coupling plate as shown in the Fig. 4. Which usually work as a support structure, it is significant to study its fatigue life. each plate is aluminum plate structure of 1 m×1 m length and 3 mm thickness, Poisson’s ratio is 0.32, The internal loss factor of each band is 0.0063. Assuming that the plate 2 is randomly excited in the center point. The force is shown in Fig. 5. Time domain force is translated into frequency domain by Fourier transform. The broad-band is divided into 10 1/3 octaves from 1 kHz to 8 kHz. The zero-order moment of the stress PSD in each octave is calculated respectively, and then the fatigue life is estimated.
Fig. 4Three coupling plate structure
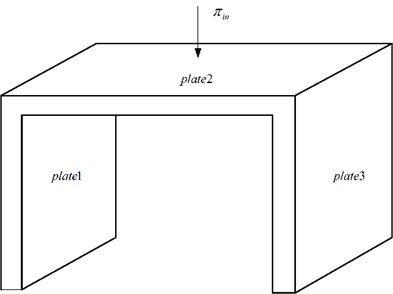
Fig. 5Force – time domain curve
Fig. 6Bending wave energy nephogram in center frequency f= 1000 Hz
a) EFEM
b) Hybrid-EFEM
The bending wave energy nephogram in center frequency 1000 Hz calculated separately by EFEM and Hybrid-EFEM was shown in Fig. 6.
From Fig. 6 we can see the energy is symmetrical due to the symmetrical structure and force. And the dangerous point is the center of plate 2. Most of all, Fig. 6 shows the stress level of the dangerous point simulated by Hybrid-EFEM is much larger than that of EFEM.
Assumed the two coefficients of the S-N curve is 3.015, 1.268×1013, The fatigue life calculated by the zero-order moment stress spectrum is shown in Table 2.
Table 2Estimated fatigue life
Methods | Zero-moment Rayleigh | Zero-moment Wirsching | Zero-moment Dirlik |
Fatigue life (h) | 50.49 | 60.79 | 60.48 |
4. Conclusions
This paper presents a new high-frequency fatigue life prediction method. Firstly, a hybrid energy method considering the direct field is introduced and extended to general coupling structure. And the equivalent stress amplitude estimation method based on the energy density is deduced. Finally, combined with the zero-order moment stress spectrum method, the structural high-frequency vibration fatigue life is predicted. An example of two coupled plate shows that the Hybrid-EFEM’s accuracy compared with EFEM, and a practical fatigue life estimation example of three coupled plate proves the new high-frequency fatigue life prediction method is feasible and scientific.
References
-
Barter J. W., Dolling D. S. Prediction of fluctuating pressure loads produced by shock-induced turbulent boundary layer separation. AIAA 96-2043, 1996.
-
Bishop N. W. M. The Use of Frequency Domain Parameters to Predict Structural Fatigue. Ph.D. Thesis, University of Warwick, UK, 1988.
-
Dirlik Dirlik T. T. Application of Computers in Fatigue Analysis. Ph.D. Thesis, University of Warwick, UK, 1985.
-
Wang Y. Y., Chen H. B., Zhou H. W. A fatigue life estimation algorithm based on Statistical Energy Analysis in high-frequency random processes. International Journal of Fatigue, Vol. 83, 2015, p. 221-229.
-
Lyon R. H. Statistical Energy Analysis of Dynamical Systems: Theory and Applications. MIT Press, Cambridge, 1997.
-
Bouthier O. M., Bernhard R. J. Simple models of the energetics of transversely vibrating plates. Journal of Sound and Vibration, Vol. 182, Issue 1, 1995, p. 149-164.
-
Smith M. J. A hybrid energy method for predicting high frequency vibrational response of point-loaded plates. Journal of Sound and Vibration, Vol. 202, Issue 3, 1997, p. 375-394.
-
Hardy P., Ichchou M., Jezequel L., Trentin D. A hybrid local energy formulation for plates mid-frequency flexural vibrations. European Journal of Mechanics, A/Solids, Vol. 28, Issue 1, 2009, p. 121-130.
About this article
This work is supported by the strategic Priority Research Program of the Chinese Academy of Sciences, Grant No. XDB22040502.
