Free vibration analysis of thin-walled curved box girder considering shear lag deformation

Cai, Heng; Lu, Hailin; Yang, Hongyin

doi:10.21595/vp.2017.18596

Vibroengineering Procedia

Browse Procedia

Published: 30 June 2017

Check for updates

Free vibration analysis of thin-walled curved box girder considering shear lag deformation

Heng Cai¹

Hailin Lu²

Hongyin Yang³

^{1, 2, 3}School of Resource and Civil Engineering, Wuhan Institute of Technology, Wuhan, China

Corresponding Author:

Hailin Lu

Cite the article Download PDF

Downloads 1506

CrossRef Citations 1

Abstract

In order to investigate dynamic shear lag effect, based on energy variation method and Hamilton principle, vibration governed differential equations of curved box girder are deduced by assuming different shear lag warping displacement modes, the explicit solution to bending frequency of curved box girder is worked out with Galerkin method. The results of a numerical example show that shear lag warping displacement functions have a limit influence on vibration frequency; second degree parabola or catenary are the appropriate shear lag warping displacement function of box girder; Compared the theoretical calculating results with numerical results of ANSYS, the error between them is only 0.57 %, they agree very well with each other, which demonstrates the correctness and reliability of theoretical deduction.

1. Introduction

Thin-walled box girder with wide flange is widely applied in the engineering construction for its merits such as great stiffness, light weight and so on. While shear lag effect [1] is a prominent problem in box girder, it means that normal stress of flange is non-uniform distributed along width direction because of flange shear deformation. This phenomenon will affect the safety and durability of box girder bridges [2]. Energy variation method, based on principle of minimum potential energy, can not only acquire closed-form solution [3, 4] but also get the real peak stress at the ribs, therefore it is widely applied in calculating shear lag.

Bridges will bear vehicle load, wind load, and sometimes seismic action when they are in service, under the impact of vehicle load and vertical seismic excitation, box girder considered curvature will create strong coupling effect of bending, torsion and shear lag effect, which will make it difficult to calculate its internal force and deformation under dynamic loads, while vibration frequency is an important parameter to reflect the dynamic characteristics of bridges especially when General code for design of highway Bridges and culverts [5] is used to calculate impact factor. Shear lag warping displacement mode is the premise and basis of energy variation method, because it can influence solution accuracy. In this paper, shear lag warping displacement modes are respectively assumed as parabola series [6-8], cosine function, exponential function and catenary, governed differential equations of curved box girder are deduced by energy variation method and Hamilton principle and the explicit solution is also acquired, meanwhile, shear lag warping displacement modes with high precision are studied.

2. System potential energy

In order to simplify mechanic model, assumptions are as following:

(1) The damp is not considered and the material is linear elastic.

(2) The flanges don’t conform to plane cross-section assumption while the webs do.

(3) Shear lag effect is only considered in vertical bending deformation.

(4) Transverse deformation and shear deformation in out-plane are neglected, they mean $ε_{y} = ε_{z} = 0$ , $γ_{y z} = γ_{x z} = 0$ .

The cross section of curved box girder is shown as Fig. 1.

Fig. 1Cross section type of curved box girder

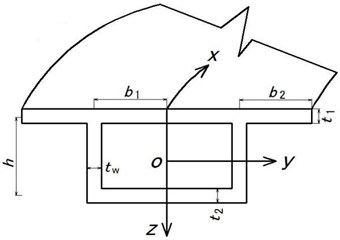
According to the assumptions above, the longitudinal shear lag warping displacement is shown as Eq. (1):

1

u (x, y, t) = ζ (y) u (x, t),

where $u (x, t)$ is maximum difference shear angle of flange and $ζ (y)$ is warping function, they are assumed to be as following:

(1) Parabola series:

2

ζ (y) = 1 - {(\frac{y}{b_{i}^{}})}^{n}, (n = 2, 3, 4, 5) .

(2) Cosine function:

3

ζ (y) = c o s (\frac{π}{2} \frac{y}{b_{i}}) .

(3) Exponential function:

4

ζ (y) = \frac{e - e^{y / b_{i}}}{e - 1} .

(4) Catenary:

5

ζ (y) = 2 - c o s h (η y), η = \frac{l n (2 + \sqrt{3})}{b_{i}},

where $b_{i} (i = 1, 2)$ are the half flange width and cantilever slab width respectively.

The total potential energy of curved box girder is shown as Eq. (6):

U = U_{w} + U_{f} + U_{t} + U_{r} = \frac{E I}{2} \int_{0}^{l} (w^{''} - \frac{ϕ}{r})^{2} d x + \frac{G I_{t}}{2} \int_{0}^{l} (ϕ^{'} + \frac{w^{'}}{r})^{2} d x \begin{array}{l} + \frac{E I_{w}}{2} \int_{0}^{l} {(ϕ^{''} + \frac{w^{''}}{r})}^{2} d x + \frac{G \bar{I_{s}}}{2} \end{array}

6

\int_{0}^{l} \frac{4 u^{2}}{3 b^{2}} d x + \frac{E I_{s}}{2} \int_{0}^{l} {(w^{''} - \frac{ϕ}{r})}^{2} + \frac{8}{15} u^{'^{2}} + \frac{3}{2} u^{'} (w^{''} - \frac{3 ϕ}{2 r}) d x,

where $U_{w}$ , $U_{f}$ are web and flange energy, and $U_{t}$ , $U_{r}$ are free torsion and restricted torsion potential energy respectively, $w$ , $ϕ$ are vertical deflection and torsion angle, $r$ is curvature radius, $h_{i} (i = 1, 2)$ are the distances from cross section center to the upper and bottom flange. Besides, $E$ , $G$ are Young’s modulus and shear modulus, $I_{t}$ , $I_{w}$ are torsional moment inertial and warping moment inertial.

The vibration energy of curved box girder can be given as Eq. (7):

7

T = \frac{1}{2} \int_{0}^{l} \bar{m} {(\frac{\partial w}{\partial t})}^{2} d x,

where $l$ , $\bar{m}$ are length and linear mass density.

3. Vibration differential equations

The generalized potential energy function is shown as Eq. (8):

8

\prod = U - T = \int_{x_{1}}^{x_{2}} F (x, u, u^{'}, \dot{w}, w^{'}, w^{''}, ϕ, ϕ^{'}, ϕ^{''}) d x .

Under the condition of small deformation, there is no external force, based on Hamilton principle $\int_{t_{1}}^{t_{2}} δ (U - T) d t = 0$ , the first variation of Eq. (8) can be got, it is shown as Eq. (9):

9

\frac{\partial F}{\partial u} - \frac{d}{d x} \frac{\partial F}{\partial u^{'}} = 0, \frac{d^{2}}{d x^{2}} \frac{\partial F}{\partial w^{''}} - \frac{d}{d x} \frac{\partial F}{\partial w^{'}} - \frac{d}{d t} \frac{\partial F}{\partial \dot{w}} = 0, \frac{d^{2}}{d x^{2}} \frac{\partial F}{\partial ϕ^{''}} - \frac{d}{d x} \frac{\partial F}{\partial ϕ^{'}} + \frac{\partial F}{\partial ϕ} = 0 .

Based on Eq. (9), the vibration differential equations can be shown as Eq. (10), and the corresponding boundary conditions are shown as Eq. (11):

10a

α E I_{s} w^{'''} - α E I_{s} \frac{ϕ^{'}}{r} + β u^{''} - η \frac{G \bar{I_{s}}}{b^{2}} u = 0,

10b

(E I + \frac{E I_{w}}{r^{2}}) w^{(4)} - \frac{G I_{t}}{r} w^{''} + \frac{E I_{w}}{r} ϕ^{(4)} - \frac{E I + G I_{t}}{r} ϕ^{''} + α E I_{s} u^{'''} + \bar{m} \overset{. .}{w} = 0,

10c

\frac{E I_{w}}{r} w^{(4)} - \frac{E I + G I_{t}}{r} w^{''} + E I_{w} ϕ^{(4)} - G I_{t} ϕ^{''} + \frac{E I}{r^{2}} ϕ - α \frac{E I_{s}}{r} u^{'} = 0,

11a

\frac{\partial F}{\partial u^{'}} δ u |_{0}^{l} = 0,

11b

(\frac{\partial F}{\partial ϕ^{'}} - \frac{d}{d x} \frac{\partial F}{\partial ϕ^{''}}) δ ϕ |_{0}^{l} = 0, \frac{\partial F}{\partial ϕ^{''}} δ ϕ^{'} |_{0}^{l} = 0,

11c

(\frac{\partial F}{\partial w^{'}} - \frac{d}{d x} \frac{\partial F}{\partial w^{''}}) δ w |_{0}^{l} = 0, \frac{\partial F}{\partial w^{''}} δ w^{'} |_{0}^{l} = 0, \frac{\partial F}{\partial \dot{w}} δ w |_{0}^{l} = 0,

where $I_{s}$ , $\bar{I_{s}}$ are inertia moment and generalized inertia moment of flange, $\bar{I_{s}} = (I_{1} / b_{1}^{2} + I_{2} / b_{2}^{2}) b^{2}$ , the number in bracket and the “pie” mean the derivative of $x$ , dot is the derivative of time $t$ , $α$ , $β$ , $η$ are shear lag warping constants.

4. Bending vibration frequency

According to Eq. (11), the displacement field functions can be given as Eq. (12) [1].

12

\{\begin{array}{l} w (x, t) = w_{0} s i n (\frac{π x}{l}) s i n (ω t + θ), \\ ϕ (x, t) = ϕ_{0} s i n (\frac{π x}{l}) s i n (ω t + θ), \\ u (x, t) = u_{0} c o s (\frac{π x}{l}) s i n (ω t + θ) . \end{array}

Take derivative of Eq. (12) and substitute them into Eq. (10), the results are shows as Eq. (13):

13a

[(E I + \frac{E I_{w}}{r^{2}}) \frac{π^{4}}{l^{4}} + \frac{G I_{t}}{r^{2}} - \bar{m} ω^{2}] w_{0} + (\frac{E I_{w}}{r} \frac{π^{4}}{l^{4}} + \frac{E I + G I_{t}}{r} \frac{π^{2}}{l^{2}}) ϕ_{0} + (α E I_{s} \frac{π^{3}}{l^{3}}) u_{0} = 0,

13b

(\frac{E I_{w}}{r} \frac{π^{4}}{l^{4}} + \frac{E I + G I_{t}}{r} \frac{π^{2}}{l^{2}}) w_{0} + (E I_{w} \frac{π^{4}}{l^{4}} + G I_{t} \frac{π^{2}}{l^{2}} + \frac{E I}{r^{2}}) ϕ_{0} + (α \frac{E I {}_{s}}{r} \frac{π}{l}) u_{0} = 0,

13c

(α E I_{s} \frac{π^{3}}{l^{3}}) w_{0} + (α \frac{E I_{s}}{r} \frac{π}{l}) ϕ_{0} + (β E I_{s} \frac{π^{2}}{l^{2}} + η \frac{G \bar{I_{s}}}{b^{2}}) u_{0} = 0 .

In the Eq. (13), there exist nonzero solution to a homogeneous linear equation of $w_{0}$ , $ϕ_{0}$ , $u_{0}$ , therefore the coefficient determinant is zero, it is shown as Eq. (14):

14

|\begin{array}{l} K_{11} & K_{12} & K_{13} \\ K_{21} & K_{22} & K_{23} \\ K_{31} & K_{32} & K_{33} \end{array}| = 0,

where:

K_{11} = (E I + \frac{E I_{w}}{r^{2}}) \frac{π^{4}}{l^{4}} + \frac{G I_{t}}{r^{2}} - \bar{m} ω^{2}, K_{12} = \frac{E I_{w}}{r} \frac{π^{4}}{l^{4}} + \frac{E I + G I_{t}}{r} \frac{π^{2}}{l^{2}}, K_{13} = α E I_{s} \frac{π^{3}}{l^{3}},

K_{22} = E I_{w} \frac{π^{4}}{l^{4}} + G I_{t} \frac{π^{2}}{l^{2}} + \frac{E I}{r^{2}}, K_{23} = α \frac{E I_{s}}{r} \frac{π}{l}, K_{33} = β E I_{s} \frac{π^{2}}{l^{2}} + η \frac{G \bar{I_{s}}}{b^{2}}, K_{21} = K_{12},

K_{31} = K_{13}, K_{32} = K_{23} .

The bending frequency of curved box girder is acquired based on Eq. (14).

5. Numerical example

The material properties and structural dimensions of curved box girder are shown in the literature [9], in this paper, dimensions are shown as Fig. 1, mass density $ρ =$ 1180 kg/m³, structural parameters: $t_{1} = t_{2} = t_{w} =$ 8 mm, $b_{1} = b_{2} = h =$ 100 mm, curvature radius $r =$ 2.5 m, curvature angle $θ =$ 30°. The material parameters are as following: Young’s modulus $E =$ 3000 MPa, Poisson’s ratio $μ =$ 0.385, the results are shown as Table 1.

In order to verify the correctness of the theoretical formula, SHELL 63 element is adopted to found the spatial shell element model of curved box girder in ANSYS. Considering boundary conditions, $U x$ , $U y$ , $U z$ and $U y$ , $U z$ are restricted at the junction between web and bottom flange, while $U x$ , $U z$ , and $U z$ are restricted in the other side, vibration model and frequency are shown as Fig. 2.

It can be seen from Table 1 and Fig. 2 that vibration frequency under different shear lag warping displacement modes are almost the same, based on principle of minimum potential energy, the corresponding vibration frequency is inevitably minimum when the energy is also minimum, therefore second degree parabola and catenary are the appropriate function of the shear lag warping displacement mode, which can better reflect the spatial mechanical behavior of curved box girder.

Besides, the calculating results in this paper agree well with the ANSYS numerical analysis, the error between them is only 0.57 %. Compared with the bridge code [5], the results in this paper have higher precision.

Table 1Bending vibration frequency (Hz)

Displacement modes		Frequency
Parabola series	Second	59.980
	Third	60.055
	Fourth	60.176
	Fifth	60.291
Cosine function		60.001
Exponential function		60.059
Catenary		59.985
ANSYS		60.323
Chinese bridge code [5]		64.403

Fig. 2Analysis results of ANSYS

6. Conclusions

The following conclusions are acquired:

(1) The theoretical results in this paper agree well with finite element analysis, which can verify the correctness and reliability of theoretical formulas.

(2) Shear lag warping displacement modes have a limit influence on vibration frequency of curved box girder.

(3) Second degree parabola and catenary can better reflect the spatial mechanical behavior of curved box girder, it is advised to preferentially adopt second degree parabola or catenary when shear lag effect is analyzed by energy variation method.

References

Xiang Haifan, Fan Lichu Advanced Theory of Bridge Structures. Second Edition, China Communication Press, Beijing, 2008.

Search CrossRef
Cai H., Lu H. L., Tang Z. 3D finite element analysis on shear lag effect of curved box girder under multi-dimensional seismic excitation. Vibroengineering Procedia, Vol. 10, 2016, p. 293-297.

Search CrossRef
Luo Qizhi Theory and Model Test Studies of the Shear Lag in Thin Walled Box Girders Based on Energy Principle. Hunan University, Hunan, 2005.

Search CrossRef
Zhou W. B., Jiang L. Z., Liu Z. J., et al. Closed-form solution to thin-walled box girders considering effects of shear deformation and shear lag. Journal of Central South University (English Edition), Vol. 19, Issue 9, 2012, p. 2650-2655.

Publisher
JTGD60. General Code for Design of Highway Bridges and Culverts. China Communication Press, Beijing, 2015.

Search CrossRef
Zhang Yuanhai, Lin Lixia Initial parameter method for analyzing shear lag effect of thin-walled box girders. Engineering Mechanics, Vol. 30, Issue 8, 2013, p. 205-211.

Search CrossRef
Lin Pengzhen, Liu Fengkui, Ji Wei Analysis on shear lag effect of concrete box beam by variational principle. Journal of the China Railway Society, Vol. 35, Issue 2, 2013, p. 93-98.

Search CrossRef
Zhang Yuhong The Experimental Study and Theoretical Analysis in Shear Lag Effect on Thin-Walled Box-Girder. Lanzhou Jiaotong University, Lanzhou, 2011.

Search CrossRef
Lu Hailin, Cai Heng, Tang Zheng Analysis on shear lag effect of thin-walled curved box girder under moving load. Railway Engineering, Vol. 9, 2016, p. 14-18.

Publisher

Cited by

Symplectic analysis of thin-walled curved box girders with torsion, distortion and shear lag warping effects

Marcello Arici | Michele Fabio Granata | Giuseppe Longo

(2022)

About this article

Received

07 May 2017

Accepted

08 May 2017

Published

30 June 2017

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/vp.2017.18596

Keywords

thin-walled curved box girder

shear lag warping displacement modes

vibration frequency

energy variation

finite element

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 04 04

Acoustic vibration analysis of high-temperature thin-walled structures

Peng Huang, Yaqi Hu, Fei Chen, Bohua Han, Hongjun Zhang

Research article

2019 05 15

Dynamic response of long-span continuous curved box girder bridge under seismic excitation

Heng Cai, Hailin Lu

Research article

2017 12 17

Analysis on shear lag effect of three-span continuous curve steel box-section girder

Hailin Lu, Kaiyi Xue, Tengfei Peng

Research article

2017 05 30

Seismic response analysis on shear lag effect of continuous curved box girder with three spans

Hailin Lu, Heng Cai, Hongyin Yang, Kaiyi Xue

H. Cai, H. Lu, and H. Yang, “Free vibration analysis of thin-walled curved box girder considering shear lag deformation,” Vibroengineering PROCEDIA, Vol. 12, pp. 24–28, Jun. 2017, https://doi.org/10.21595/vp.2017.18596

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2017.18596
UR  - https://doi.org/10.21595/vp.2017.18596
TI  - Free vibration analysis of thin-walled curved box girder considering shear lag deformation
T2  - Vibroengineering PROCEDIA
AU  - Lu, Hailin
AU  - Cai, Heng
AU  - Yang, Hongyin
PY  - 2017
DA  - 2017/06/30
PB  - JVE International Ltd.
SP  - 24-28
VL  - 12
SN  - 2345-0533
ER  - 

Copy Ris

Copied to clipboard!

@article{Lu_2017,
	doi = {10.21595/vp.2017.18596},
	url = {https://doi.org/10.21595/vp.2017.18596},
	year = 2017,
	month = {jun},
	publisher = {{JVE} International Ltd.},
	volume = {12},
	pages = {24--28},
	author = {Hailin Lu and Heng Cai and Hongyin Yang},
	title = {Free vibration analysis of thin-walled curved box girder considering shear lag deformation},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]H. Lu, H. Cai, and H. Yang, “Free vibration analysis of thin-walled curved box girder considering shear lag deformation,” Vibroengineering PROCEDIA, vol. 12, pp. 24–28, Jun. 2017, doi: 10.21595/vp.2017.18596.

Copy IEEE

Copied to clipboard!

Lu, Hailin, Heng Cai, and Hongyin Yang. “Free Vibration Analysis of Thin-Walled Curved Box Girder Considering Shear Lag Deformation.” Vibroengineering PROCEDIA 12 (June 30, 2017): 24–28. https://doi.org/10.21595/vp.2017.18596.

Copy Chicago

Copied to clipboard!

Free vibration analysis of thin-walled curved box girder considering shear lag deformation

Abstract

1. Introduction

2. System potential energy

3. Vibration differential equations

4. Bending vibration frequency

5. Numerical example

6. Conclusions

References

Cited by

About this article

Related Articles