Analysis on natural characteristics of four-stage main transmission system in three-engine helicopter

Chen, Yuan; Zhu, Ru-peng; Xiong, Ye-ping; Jin, Guang-hu

doi:10.21595/vp.2017.18558

Vibroengineering Procedia

Browse Procedia

Published: 30 June 2017

Check for updates

Analysis on natural characteristics of four-stage main transmission system in three-engine helicopter

Yuan Chen¹

Ru-peng Zhu²

Ye-ping Xiong³

Guang-hu Jin⁴

^{1, 2, 4}College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China

³Engineering and the Environment University of Southampton, Boldrewood Innovation Campus SO16 7QF, Southampton, United Kingdom

Corresponding Author:

Ye-ping Xiong

Cite the article Download PDF

Downloads 1657

CrossRef Citations 4

Abstract

The vibration model of four-stage main transmission system in helicopter was established through lumped mass method. In the model, many factors, including time-varying meshing stiffness and torsional stiffness of gear shaft were considered. The differential equation of the system was solved via Fourier method, and the influence of the torsional stiffness of shafts on the first five orders of the system’s natural frequency was studied. Some theoretical results were summarized as guidelines for further research and design of four-stage deceleration helicopter at last.

1. Introduction

The four-stage main transmission system has the ability to carry heavy load, and it has an essential effect in dynamic behavior in three-engine helicopters. Predicting natural characteristics might protect the whole system from further failure and damage. However, its structure is extremely complicated, it has multiple branches of input and output, along with long transmission chain which includes numerous gears and accessories [1]. In addition, mutual coupling exists in each branch and whole system, and the system is affected by several dynamic factors like time-varying meshing stiffness, clearance and synthetic transmission error. Furthermore, the input speed of engine is greatly high which has huge effect on the vibration of the system. Therefore, it is urgent and meaningful to analyze and study its vibration characteristics.

For the vibration characteristics of helicopter main transmission system, scholars study the modal vibration of complex multi-shaft system of a variety of gear pair meshing [2], and analyze the influence of meshing stiffness, installation angle, spiral angle and bearing stiffness on the natural characteristics of the system [3, 4].

On the other hand, in terms of the planetary gear chain of main transmission system, the effects of torque on dynamic behavior in torsional model are analyzed [5, 6]. Other studies of planetary gear dynamics include mesh stiffness variation and load-sharing [7], influence of free vibration [8, 9], and tooth crack detection [10].

In conclusion, most studies are limited in planetary chain system or the components of helicopter’s main reducer, few of them involve the overall components of main transmission system, which has long chain and multiple DOF. Besides, it is presently still difficult to analyze the impact of torsional stiffness of shaft on the vibration characteristics. Therefore, in the paper, the influence of the changes of torsional stiffness on various orders of natural frequency was explored, and theoretical support was provided for the design of the helicopter.

2. Dynamic modeling of the system

The dynamic model of four-stage deceleration helicopter’s transmission system is shown in Fig. 1. In the picture, the system has three same input branches, namely $j$ branch ( $j =$ 1, 2, 3). Each branch has 5 gears. $θ_{1}^{(j)}$ , $θ_{2}^{(j)}$ , $θ_{3}^{(j)}$ , $θ_{4}^{(j)}$ , $θ_{5}^{(j)}$ , $θ_{6}$ , $θ_{c}$ , $θ_{7}$ , $θ_{8}$ , $θ_{9}$ $θ_{s}$ and $θ_{p i}$ are rotational DOF of gear system in each stage deceleration.

$k_{23}$ , $k_{45}$ , $k_{78}$ _, $k_{i n}$ , $k_{o u t}$ and $k_{6 s}$ are torsional stiffness of shafts connecting each gear pair; $c_{12}$ , $c_{34}$ , $c_{56}$ , $c_{s p i}$ and $c_{r p i}$ are meshing damping of each gear pair; $k_{12}$ , $k_{34}$ , $k_{56}$ , $k_{s p i}$ and $k_{r p i}$ are meshing stiffness of each gear pair. The flexibility between the shafts and transverse DOF are not taken into account due to its weak influence on natural frequency.

Fig. 1Model of three-engine helicopter transmission system

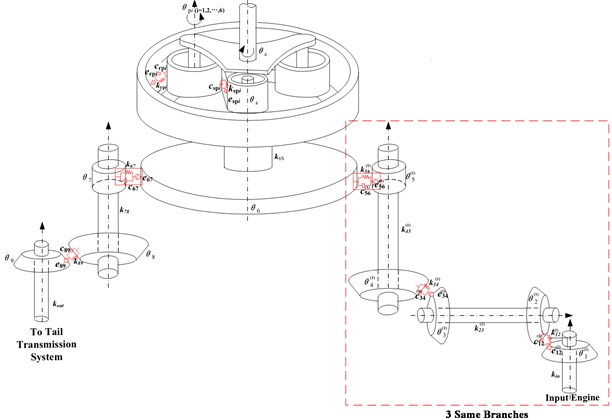
The differential equation of the trial model system can be deduced through Newton’s law, as shown below:

1

\{\begin{array}{l} J_{1} {\ddot{θ}}_{1}^{(j)} + [F_{1_2}^{p (j)} (t) + F_{1_2}^{d (j)} (t)] r_{1} + k_{i n} {θ_{1}}^{(j)} = T_{E j}, \\ J_{2} {\ddot{θ}}_{2}^{(j)} - [F_{1_2}^{p (j)} (t) + F_{1_2}^{d (j)} (t)] r_{2} + {k_{23}}^{(j)} ({θ_{2}}^{(j)} - {θ_{3}}^{(j)}) = 0, \\ J_{3} {\ddot{θ}}_{3}^{(j)} + [F_{3_4}^{p (j)} (t) + F_{3_4}^{d (j)} (t)] r_{3} + {k_{23}}^{(j)} ({θ_{3}}^{(j)} - {θ_{2}}^{(j)}) = 0, \\ J_{4} {\ddot{θ}}_{4}^{(j)} - [F_{3_4}^{p (j)} (t) + F_{3_4}^{d (j)} (t)] r_{4} + {k_{45}}^{(j)} ({θ_{4}}^{(j)} - {θ_{5}}^{(j)}) = 0, \\ J_{5} {\ddot{θ}}_{5}^{(j)} + [F_{5_6}^{p (j)} (t) + F_{5_6}^{d (j)} (t)] r_{5} + {k_{45}}^{(j)} ({θ_{5}}^{(j)} - {θ_{4}}^{(j)}) = 0, \\ J_{6} {\ddot{θ}}_{6} - \sum_{j = 1}^{3} [F_{5_{6}}^{p (j)} (t) + F_{5_{6}}^{d (j)} (t)] r_{6} + [F_{6_{7}}^{p} (t) + F_{6_{7}}^{d} (t)] r_{6} + k_{6 s} (θ_{6} - θ_{s}) = 0, \\ J_{7} {\ddot{θ}}_{7} - [F_{6_7}^{p} (t) + F_{6_7}^{d} (t)] r_{7} + k_{78} (θ_{7} - θ_{8}) = 0, \\ J_{8} {\ddot{θ}}_{8} + [F_{8_9}^{p} (t) + F_{8_9}^{d} (t)] r_{8} + k_{78} (θ_{8} - θ_{7}) = 0, \\ J_{9} {\ddot{θ}}_{9} - [F_{8_{9}}^{p} (t) + F_{8_{9}}^{d} (t)] r_{9} + k_{o u t} θ_{9} = - T_{R R}, \\ J_{s} {\ddot{θ}}_{s} + \sum_{i = 1}^{N} (F_{s p i}^{p} + F_{s p i}^{d}) r_{s} - k_{6 s} (θ_{6} - θ_{s}) = 0, \\ J_{p} {\ddot{θ}}_{p i} - (F_{s p i}^{p} + F_{s p i}^{d}) r_{p} + (F_{r p i}^{p} + F_{r p i}^{d}) r_{p} = 0, \\ [J_{c} + \sum_{i = 1}^{N} (m_{p i} r_{c}^{2})] {\ddot{θ}}_{c} - \sum_{i = 1}^{N} (F_{s p i}^{p} + F_{s p i}^{d} + F_{r p i}^{p} + F_{r p i}^{d}) r_{c} c o s α = - T_{M R}, \end{array}

where $T_{E j}$ is denoted as the output torque of engine $j$ ( $j =$ 1, 2, 3); $T_{R R}$ and $T_{M R}$ are the output torque of tail branch and planet carrier. $F^{p}$ and $F^{d}$ are dynamic meshing and damping forces of each gear pair.

In addition, after the decomposition and recombination of Eq. (1), it can be expressed with following matrix-vector form:

2

[M] \{\ddot{X}\} + [C] \{\dot{X}\} + [K] \{X\} = \{F\} .

Here [ $M$ ], [ $C$ ], [ $K$ ] are the mass matrix, damping matrix and stiffness matrix of the governing equation, and all matrices are in 27 dimension; matrix [ $F$ ] is external excitation.

3. System natural characteristics analysis

A set of basic parameters are extracted from a geared system, listed in Table 1. By setting the value of damping item and external excitation item in Eq. (2) to be zero, the vibration differential equation of the system under free condition can be obtained.

Table 1Gear parameters

	Tooth number	Module	Face width (mm)	Initial phase of meshing stiffness (°)
Gear 1 (First stage)	30	4.5	40	0
Gear 2 (First stage)	85	4.5	40	0
Gear 3 (Second stage)	40	5	60	20
Gear 4 (Second stage)	90	5	60	20
Gear 5 (Third stage)	25	4.75	40	30
Gear 6 (Third stage)	142	4.75	40	30
Gear 7 (Tail branch)	40	5	35	0
Gear 8 (Tail branch)	60	5	35	0
Gear 9 (Tail branch)	70	5	40	20
Gear 10 (Sun gear in fourth stage)	68	5	40	20
Gear 11 (Planet gear in fourth stage)	37	5	40	$\emptyset_{s p 1} = 0$ , $\emptyset_{s p 2} = π / 3$ , $\emptyset_{s p 3} = 2 π / 3$ , $\emptyset_{s p 4} = 2.5 π / 3$ , $\emptyset_{s p 5} = π$ , $\emptyset_{s p 6} = 4 π / 3$

The helicopter has multiple stage deceleration shaft system. $k$ is torsional stiffness of each gear pair. The change of the value of torsional stiffness means the change of stiffness matrix, affecting natural frequency accordingly. In the paper, torsional stiffness of shafts was changed; the influence of change of torsional stiffness on the natural characteristics was explored; theoretical support was provided for the design of the helicopter shaft.

Fig. 2(a) indicates the impact of input shaft torsional stiffness on natural frequency. It shows that the values of natural frequency are close and at the low frequency regions when input shaft torsional stiffness is lower; acceleration of rotational speed tends to cause resonance, so the shaft is key shaft; in case of resonance, it has bigger impact on planet chain and tail transmission system. In addition, when torsional stiffness is greater than 8×10⁴N·m/rad, 1st order natural frequency remains 640 Hz, while natural frequency of the rest orders continues to increase; when torsional stiffness is greater than 2×10⁵ N·m/rad, 2nd order natural frequency remains 1100 Hz, while natural frequency of the rest orders gradually tends to be stable and at high frequency areas with the increase of torsional stiffness. Moreover, 3rd order natural frequency always increases with the increase of torsional stiffness, and doesn’t become gradually stable until torsional stiffness is higher.

Fig. 2(b) is the impact of torsional stiffness of Gear 2 and Gear 3 connecting shaft on natural frequency, showing similar laws to Fig. 2(a). However, 2nd order natural frequency doesn’t remain stable at 1100 Hz until torsional stiffness is greater than 4.5×10⁵ N·m/rad. At the same time, the abrupt change point of the 5th order is delayed to 4.5×10⁵ N·m/rad.

Fig. 2(c) shows the impact of torsional stiffness of Gear 4 and Gear 5 connecting shaft on natural frequency. It can be seen that the change of torsional stiffness slightly impacts first 4 orders natural frequency; 5th order natural frequency rises slightly with the increase of torsional stiffness, and is in the high frequency regions.

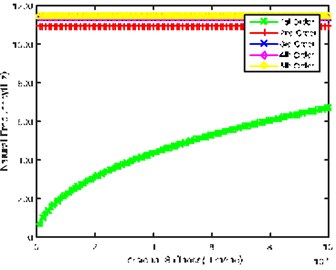
Fig. 2(d) shows the impact of torsional stiffness of sun gear input shaft on natural frequency. It can be seen that 1st order natural frequency almost shows linear increase, while natural frequency of other orders shows little change along with the increase of torsional stiffness; it crosses the low frequency regions when torsional stiffness is lower, so the shaft is also key shaft, and its torsional stiffness can’t be too low.

Fig. 2Impact of each shaft’s torsional stiffness on first five orders natural frequency

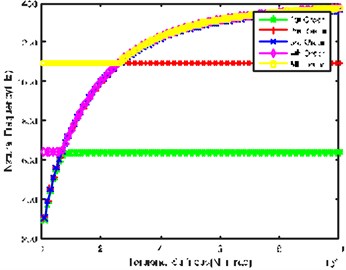
a) $k_{i n}$

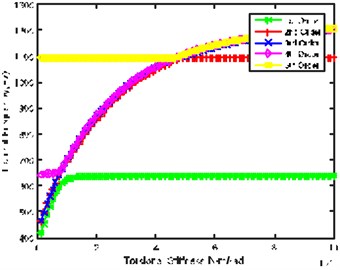
b) $k_{23}$

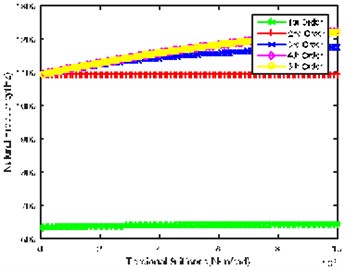
c) $k_{45}$

d) $k_{6 s}$

e) $k_{78}$

f) $k_{o u t}$

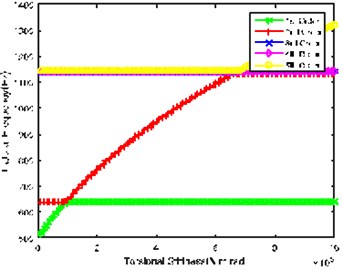
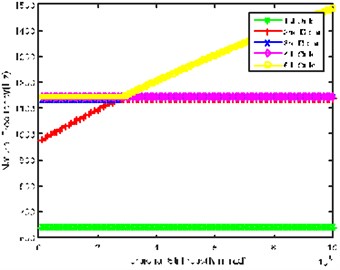
Fig. 2(e) and Fig. 2(f) respectively show the influence of Gear 7 and Gear 8 connecting shaft and tail branch’s output shaft on natural frequency. The values of natural frequency of all orders show similar trends and laws with the change of torsional stiffness. However, the stable point of 2nd order and the abrupt change point of 5th order natural frequency in Fig. 2(e) are 6.5×10⁵ N·m/rad, while the corresponding value in Fig. 2(f) is 3×10⁵ N m/rad, indicating that Gear 7 and Gear 8 connecting shaft is relatively important in tail transmission branch.

Through the comprehensive comparison of above figures, it can be found that system input shaft and sun gear input shaft have greater influence on 1st natural frequency; system input shaft and Gear 2 and Gear 3 connecting shaft have greater influence on 2nd natural frequency.

4. Conclusions

In this paper, a new dynamics model of four-stage helicopter transmission system is proposed and the analysis results enable us to draw the following conclusions:

System input shaft and the sun gear input shaft are the key shafts of the system due to their torsional stiffness affecting the low frequency region much more than other shafts.

Input shaft of the system as well as Gear 2 and Gear 3 connecting shafts greatly impact on the second order and third order natural frequency.

Gear 7 and Gear 8 connecting shaft is the most important shaft in tail transmission branch.

References

Bianchi A., Rossi S. Modeling and finite element analysis of a complex helicopter transmission including housing, shafts and gears. 1997.

Search CrossRef
Kahraman A., Zini D. M., Kienzle K. Dynamic analysis of a multi-shaft helical gear transmission by finite elements: model and experiment. ASME Journal of Vibrations and Acoustics, Vol. 126, Issue 3, 2004, p. 398-406.

Publisher
Huang J., Zhang S., Zhang Y. The influences of system parameters on the natural characteristics of a parallel multi-shaft gear-rotor system. Machinery Design and Manufacture, Vol. 7, 2013, p. 15-17, (in Chinese).

Search CrossRef
Gu Z., Yang J. Analyses of torsional vibration characteristics for transmission system of helicopter. Journal of Nanjing University of Aeronautics and Astronautics, Vol. 29, Issue 6, 1997, p. 674-678, (in Chinese).

Search CrossRef
Ericson T. M., Parker R. G. Experimental measurement of the effects of torque on the dynamic behavior and system parameters of planetary gears. Mechanism and Machine Theory, Vol. 74, 2014, p. 370-389.

Publisher
Saada A., Velex P. An extended model for the analysis of the dynamic behavior of planetary trains. Journal of Mechanical Design, Vol. 117, Issue 2A, 1995, p. 241-247.

Publisher
Kasuba R., August R. Gear mesh stiffness and load sharing in planetary gearing. ASME Paper 84-DET-229, 1984.

Search CrossRef
Zhang L., Wang Y., Wu K., et al. Dynamic modeling and vibration characteristics of a two-stage closed-form planetary gear train. Mechanism and Machine Theory, Vol. 97, 2016, p. 12-28.

Publisher
Noll M. C., Godfrey J. W., Schelenz R., et al. Analysis of time-domain signals of piezoelectric strain sensors on slow spinning planetary gearboxes. Mechanical Systems and Signal Processing, Vol. 72, 2016, p. 727-744.

Publisher
Liang X., Zuo M. J., Hoseini M. R. Vibration signal modeling of a planetary gear set for tooth crack detection. Engineering Failure Analysis, Vol. 48, 2015, p. 185-200.

Publisher

Cited by

Designing of Drive Systems in the Aspect of the Desired Spectrum of Operation

(2021)

Dynamic analysis on single-rotor multi-input helicopter main gearbox related with structural parameters

Wei Zhang | Luling An

(2021)

A New Mathematical Modeling Method for Four‐Stage Helicopter Main Gearbox and Dynamic Response Optimization

(2019)

Influence of oil film stiffness on natural characteristics of single-rotor three-input helicopter main gearbox

Yuan Chen | Ru Peng Zhu | Zai Chun Feng | Guang Hu Jin | Wei Zhang

(2018)

About this article

Received

27 April 2017

Accepted

29 April 2017

Published

30 June 2017

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/vp.2017.18558

Keywords

helicopter transmission system

four-stage reducer

natural characteristics

torsional stiffness

nonlinear dynamics

Acknowledgements

This work is supported by the National Natural Science Foundation of PRC (Grant No. 51375226 and 51475226), China Scholarship Council (Grant No. 201606830019) and Postgraduate Research and Practice Innovation Program of Jiangsu Province.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2020 06 29

Nonlinear dynamic analysis of GTF gearbox

Siyu Wang, Rupeng Zhu

Research article

2020 04 02

Nonlinear dynamic characteristics of face gear pair for helicopter

Wang Li, Ning Zhao

Research article

2018 08 15

Influence of shaft torsional stiffness on natural characteristics of four-stage main transmission system in three-engine helicopter

Yuan Chen, Ru Peng Zhu, Ye Ping Xiong, Guang Hu Jin

Research article

2018 08 15

Tooth surface friction and its influence on dynamic transmission error of double power input transmission system

G. H. Jin, H. Y. Yang, R. P. Zhu

Y. Chen, R.- Zhu, Y.- Xiong, and G.- Jin, “Analysis on natural characteristics of four-stage main transmission system in three-engine helicopter,” Vibroengineering PROCEDIA, Vol. 12, pp. 19–23, Jun. 2017, https://doi.org/10.21595/vp.2017.18558

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2017.18558
UR  - https://doi.org/10.21595/vp.2017.18558
TI  - Analysis on natural characteristics of four-stage main transmission system in three-engine helicopter
T2  - Vibroengineering PROCEDIA
AU  - Xiong, Ye-ping
AU  - Chen, Yuan
AU  - Zhu, Ru-peng
AU  - Jin, Guang-hu
PY  - 2017
DA  - 2017/06/30
PB  - JVE International Ltd.
SP  - 19-23
VL  - 12
SN  - 2345-0533
ER  - 

Copy Ris

Copied to clipboard!

@article{Xiong_2017,
	doi = {10.21595/vp.2017.18558},
	url = {https://doi.org/10.21595/vp.2017.18558},
	year = 2017,
	month = {jun},
	publisher = {{JVE} International Ltd.},
	volume = {12},
	pages = {19--23},
	author = {Ye-ping Xiong and Yuan Chen and Ru-peng Zhu and Guang-hu Jin},
	title = {Analysis on natural characteristics of four-stage main transmission system in three-engine helicopter},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]Y. Xiong, Y. Chen, R. Zhu, and G. Jin, “Analysis on natural characteristics of four-stage main transmission system in three-engine helicopter,” Vibroengineering PROCEDIA, vol. 12, pp. 19–23, Jun. 2017, doi: 10.21595/vp.2017.18558.

Copy IEEE

Copied to clipboard!

Xiong, Ye-ping, Yuan Chen, Ru-peng Zhu, and Guang-hu Jin. “Analysis on Natural Characteristics of Four-Stage Main Transmission System in Three-Engine Helicopter.” Vibroengineering PROCEDIA 12 (June 30, 2017): 19–23. https://doi.org/10.21595/vp.2017.18558.

Copy Chicago

Copied to clipboard!

Analysis on natural characteristics of four-stage main transmission system in three-engine helicopter

Abstract

1. Introduction

2. Dynamic modeling of the system

3. System natural characteristics analysis

4. Conclusions

References

Cited by

About this article

Related Articles