Predictions of input pinion floating on concentric face gear transmission static load sharing

Keywords: concentric face gear transmission, input pinion floating, static load sharing.

1. Introduction

The concentric face gear transmission shows the advantages in weight, transmission efficiency and reliability, compared with the traditional gear torque split transmission. Therefore, it is focused by the helicopter transmission researchers.

For the gear split torque transmission, uneven load distribution on gears is one of the key problems for the split transmission design. Therefore, many scholars studied the load sharing behavior of various split transmission, such as planetary gear transmissions [1-5], cylindrical gear split torque transmissions [6-12] and traditional face gear split torque transmissions [13-15]. However, there are few studies on the concentric face gear transmission. Thus, in the paper, the static load sharing of the concentric face gear transmission is studied. A static load sharing analysis model and a static load sharing calculation method associated with the input pinion floating are constructed. Then, the influence of the floating support stiffness on the static load sharing of the system is simulated. The results would be helpful to the concentric face gear transmission design.

2. Analysis model and calculation method constructions

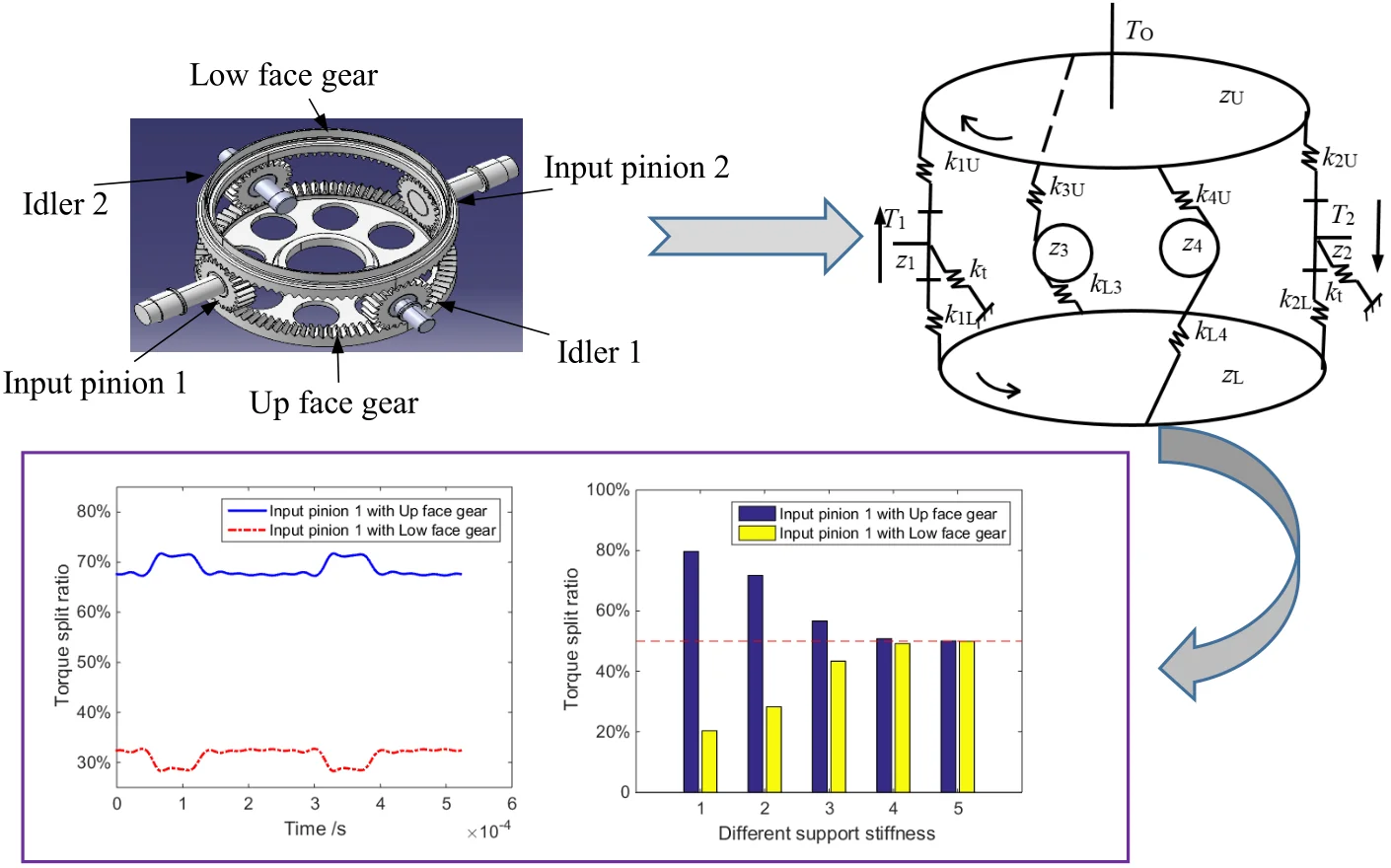
The concentric face gear transmission is composed of two coaxial face gears, two input pinions and two idler gears, as show in Fig. 1. In the system, torque split to upper and lower face gears by two input pinions, the low face gear transfers torque to the up face gear by the idler gears, and the torque is output by the upper face gear finally. The static load sharing model associated with the input pinion floating is proposed, as shown in Fig. 2.

Illustrated in Fig. 2., $Z_1$ and $Z_2$ are the input pinions, $Z_3$ and $Z_4$ are the idlers, $Z_U$ and $Z_L$ are the upper and lower face gears, $T_1$ and $T_2$ are the input torques, $T_O$ is the output torque, $k_t$ is the floating support stiffness, $k_{ij}$ is the mesh stiffness. Moreover, $F_{ij}$ is defined as the mesh force between gear $j$ and gear $i$.

Based on the equilibrium conditions, the static load sharing equation is obtained by:

(1)

$\left\{\begin{array}{l}\left(F_{1U}+F_{1L}\right)\mathrm{c}\mathrm{o}\mathrm{s}\alpha =T_1/r_{b1},\\ \left(F_{2U}+F_{2L}\right)\mathrm{c}\mathrm{o}\mathrm{s}\alpha =T_2/r_{b1},\\ F_{3U}-F_{L3}=0,\\ F_{4U}-F_{L4}=0,\\ \left(-{F_1}_L-{F_2}_L+F_{L3}+F_{L4}\right)\mathrm{c}\mathrm{o}\mathrm{s}\alpha =0,\end{array}\right.$

and the floating support equation could be derived by:

(2)

$\left\{\begin{array}{l}{F}_{1U}-F_{1L}-k_t{s}_1=0,\\ F_{2U}-F_{2L}-k_t{s}_2=0,\end{array}\right.$

and the gear meshing force could be expressed as:

(3)

$F_{ij}=k_{ij}{r}_{bi}{\phi }_{ij},$

where, $r_{ib}$ is the gear $i$ base circle radius, and ${\phi }_{ij}$ is the deflection angle between the gear $i$ and the gear $j$.

Fig. 1. The concentric face gear transmission

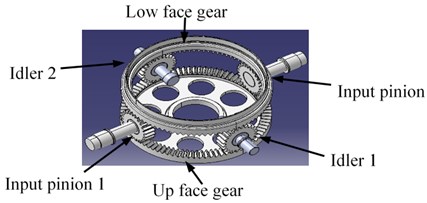
Fig. 2. The static load sharing model

For static load sharing of input pinions, the distribution ratio and maximum distribution ratio between upper and lower face gears could be obtained by:

(4)

$\left\{\begin{array}{l}{\mathrm{\Omega }}_{iU}=\frac{F_{iU}}{T_i/r_{bi}},\\ {\mathrm{\Omega }}_{iL}=\frac{F_{iL}}{T_i/r_{bi}},\mathrm{ }\mathrm{ }\mathrm{ }\mathrm{ }i=1,\mathrm{ }2,\end{array}\right.$

(5)

${\mathrm{\Omega }}_{\mathrm{m}\mathrm{a}\mathrm{x}}=\mathrm{m}\mathrm{a}\mathrm{x}\left({\mathrm{\Omega }}_{iU},{\mathrm{\Omega }}_{iL}\right).$

3. Simulations

In order to predict the influence of floating support stiffness on static load sharing of the concentric face gear transmission, the parameters of an example case are listed in Table 1.

Table 1. Parameters of system

Symbol name	Value	Unit
Modulus / $m$	4	mm
Pressure angle / $\alpha$	20	°
Tooth number of face gear / $z_f$	86	–
Tooth number of cylindrical gears / $z_p$	24	–
Tooth number of shaper / $z_t$	25	–
Addendum coefficient / $h_a^{*}$	1	–
Clearance coefficient / $c^{*}$	0.25	–

Fig. 3. Static load sharing with different floating support stiffness

a) Without floating (1)

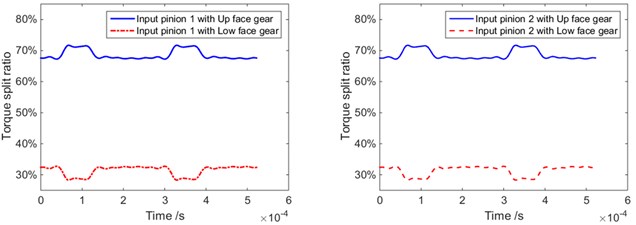
b) Floating support stiffness 10⁹N/m (2)

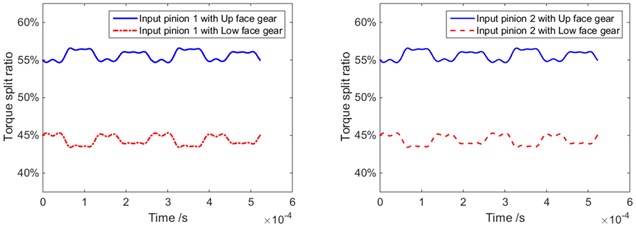
c) Floating support stiffness 10⁸N/m (3)

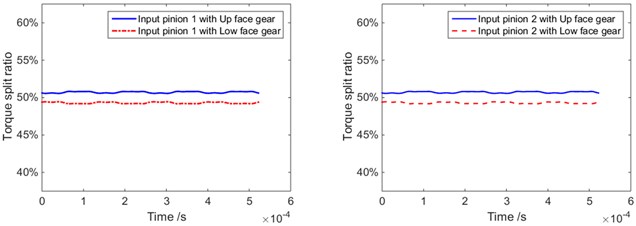
d) Floating support stiffness 10⁷N/m (4)

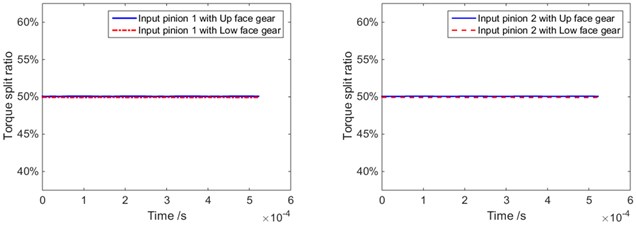
e) Floating support stiffness 10⁶N/m (5)

According to the static load sharing model and calculation method, as well as the parameters listed in Table 1, the influences of the input pinion floating on the static load sharing are simulated. The results are shown in Fig. 3 and Fig. 4.

Fig. 4. Maximum static load sharing under different floating support stiffness

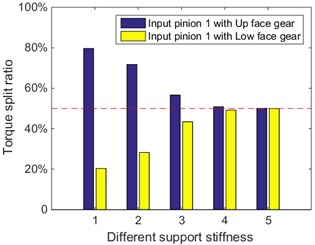
a) Input pinion 1

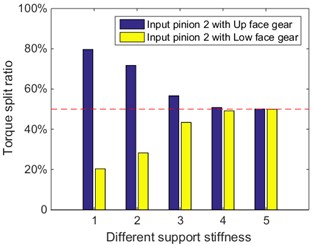
b) Input pinion 2

4. Conclusions

The works of the issue are as follows:

1) The static load sharing model and calculation method of the concentric face gear transmission associated with the input pinion floating are proposed.

2) The influences of floating support stiffness on static load sharings are simulated, and the results indicate the floating support stiffness reduction is benefit for static load sharings.

These contributions would be helpful to the concentric face gear transmission design.

Acknowledgements

References

1. Kahraman A. Load sharing characteristics of planetary transmissions. Mechanism and Machine Theory, Vol. 29, Issue 8, 1994, p. 1151-1165. [Publisher]
2. Kahraman A. Planetary gear train dynamics. Journal of Mechanical Design, Vol. 116, Issue 3, 1994, p. 713-720. [Publisher]
3. Kahraman A. Static load sharing characteristics of transmission planetary gear sets: model and experiment. SAE Technical Papers, 1999. [Publisher]
4. Lu J. H., Li B., Zhu R. P. Analysis of static load sharing in planetary gearing. Mechanical Science and Technology, Vol. 24, Issue 6, 2005, p. 702-704+709, (in Chinese). [Search CrossRef]
5. Ye F. M., Zhu R. P., Bao H. Y., et al. Dynamic load-sharing behaviors of planetary gear train system with unequal moduli and pressure angles. Journal of south China University of Technology (Natural Science Edition), Vol. 39, Issue 1, 2011, p. 117-123, (in Chinese). [Search CrossRef]
6. Krantz T. L. A Method to Analyze and Optimize the Load Sharing of Split Path Transmissions. NASA Technical Memorandum 107201, 1996. [Search CrossRef]
7. Krantz T. L., Delgado I. R. Experimental Study of Split-Path Transmission Load Sharing. NASA Technical Memorandum 107202, 1996. [Search CrossRef]
8. Gui Y. F. Analysis of Load Sharing Characteristics of Gear Split-Torque Transmission System with Elastic Quill Shafting. Nanjing University of Aeronautics and Astronautics, 2014, (in Chinese). [Search CrossRef]
9. Gui Y. F., Zhu R. P., Jin G. H., et al. Dynamic and load sharing characteristic analysis of a nonlinear cylindrical gear split-torque transmission system with backlash. Journal of Vibration and Shock, Vol. 33, Issue 18, 2014, p. 177-184, (in Chinese). [Search CrossRef]
10. Gui Y. F., Zhu R. P., Fu B. B., et al. Impact of torsional stiffness on dynamic load sharing coefficient of two-input cylindrical gear split-torque transmission system. Journal of Aerospace Power, Vol. 29, Issue 9, 2014, p. 2264-2272, (in Chinese). [Search CrossRef]
11. Li Z. J., Zhu R. P., Bao H. Y., et al. Tooth matching of split torque transmission. Journal of Central South University (Science and Technology), Vol. 45, Issue 2, 2014, p. 414-420, (in Chinese). [Search CrossRef]
12. Li Z. J. Design Methods of Split Torque Transmission System and Dynamic Analysis of Split Torque Gear Pairs. Nanjing University of Aeronautics and Astronautics, 2013, (in Chinese). [Search CrossRef]
13. Zhao N., Wang R. F., Jai Q. J. Study on the load sharing of face gear split torque transmission system. Journal of Mechanical Transmission, Vol. 37, Issue 12, 2013, p. 5-8, (in Chinese). [Publisher]
14. Peng X. L., Zhang L. Study on torque distribution of torque split transmission system of face gear. Journal of Mechanical Transmission, Vol. 40, Issue 11, 2016, p. 117-122, (in Chinese). [Search CrossRef]
15. Ren W. Design and Load Sharing Analysis of Twice Split-Torque Transmission System with Face Gears and Cylindrical Gears. Nanjing University of Aeronautics and Astronautics, 2017, (in Chinese). [Search CrossRef]

Cited By