Abstract
The static transmission error is one of the key incentives of gear dynamics and addressed by many scholars. However, the traditional calculation method of static transmission errors of spur gears does not take into account the influence of thermo-elastic coupling caused by the gear temperature field, and it limits the accuracy of the dynamic characteristic analysis. Thus, in this study, the calculation method of static transmission errors associated with thermo-elastic coupling is proposed. Furthermore, the differences between static transmission errors associated with thermo-elastic coupling contacts and traditional method of gear is discussed. The study is helpful to improve the accuracy of dynamic analysis of gear transmission system.
1. Introduction
The heat deformations caused by the uneven temperature field distribution of the gears is coupled with the elastic deformation when the gears mesh, resulting in tooth profile and tooth shape deviations, which cause many problems such as interference, vibration, and noise [1-7]. However, the traditional calculation method of the static transmission errors of gears does not consider the influence of the temperature field. Therefore, analyzing the steady-state temperature field of the gear, the heat deformations of gear and the static transmission errors will improve the analysis accuracy of the dynamic characteristics of the gear transmission system, and it can be used for gear manufacturing, tooth profile modification, vibration reduction and noise reduction.
2. Solutions of static transmission errors associated with thermo-elastic coupling contacts
First, the heat flow density and convective heat transfer coefficient of gears are calculated according to heat transfer and tribology [8]. Then add material properties, solve the steady-state temperature field, import the steady-state temperature field into the contact stress analysis of the gear by finite element analysis [9], and then set the contacts pair and restraint to obtain the thermo-elastic coupling deformation and stress value of the gear. Transform the deformation of thermo-elastic coupling contacts of gears into the direction of the meshing line and substituting the deformation amount of the driving and driven gears into the calculation formula of static transmission error. The static transmission errors associated with thermo-elastic cooling is obtained.
2.1. Calculation of key parameters of thermo-elastic coupling contacts
The heat flux and convection heat transfer coefficient are key parameters of thermo-elastic coupling temperature field of spur gears.
According to the reference [9-12], the heat flux of gear tooth surface can be written in:
where is the heat flux of meshing surface of the driving gear, is the heat flux of meshing surface of driven gear. is the half degree of contact bandwidth at the gear meshing point, is the instantaneous heat flow input on the surface of gear meshing tooth, is the angular velocity of gear, is the tangential velocity at the gear meshing point. Differentiating the driving and driven gear with the subscript 1 and 2.
According to the reference [10], the convective heat transfer coefficient of gear meshing surface can be written in:
where is the thermal conductivity of lubricating oil, is the density of lubricating oil, is the specific heat capacity of lubricating oil, is the temperature coefficient of lubricating oil, is the kinematic viscosity of lubricating oil at the temperature of oil supply, the radius of the indexing circle of a gear, is the height of the gear tooth, is the standardized cooling capacity.
The convection heat transfer coefficient of the gear face can be written in:
where is the Nusselt number of the mixture of air and lubricating oil. is the Prandtl number of the mixture of air and lubricating oil. is the thermal conductivity of mixture of air and lubricating oil. is the rotation radius of the meshing point. is the kinematic viscosity of ai and lubricating oil. is a constant that represents the temperature variation along the radial direction of the disc surface.
2.2. Calculation method of static transmission errors
According to the reference [11], thermo-elastic coupling contacts analysis of gears can use indirect coupling method by finite element analysis. The deformation of the driving and driven gear in the direction of the meshing line is obtained through thermo-elastic finite element analysis. The elastic contact equation in gear transmission can be given in [11]:
where [] is the stiffness matrix. is the node displacement vector. is the load vector. is the contact force vector.
According to the heat-transfer process, the thermal balance equations for gear transmission system can be written in:
where [] is the temperature stiffness matrix. is the node temperature vector. is thermal flow vector of generalized node.
Elastic contact and thermal contact are solved by iterative coupling according to Eq. (4) and Eq. (5). The deformation of the meshing point can be obtained in the node displacement vector . The STE formula associated with thermo-elastic coupling contacts spur gear pair can be expressed as:
where is the deformation along the direction of the meshing ling of thermo-elastic coupling contacts. Differentiating the driving and driven gear with the subscript 1 and 2. is the system equivalent error which is caused by machining and assembly errors, and it can be derived by:
where is pitch error. is tooth profile error. is tooth error, is center distance installation error. is gear pressure angle.
2.3. Differences between static transmission errors with and without thermo-elastic coupling contacts
The static transmission errors without thermo-elasti coupling contacts is mainly calculated by the equivalent tooth profile method based on material mechanics. The equivalent tooth shape method simplifies the gear teeth to variable-section cantilever beam based on elastic mechanics. According to the reference [2], it is considered that the comprehensive elastic deformation of the meshing tooth consists of the bending deformation of the rectangular and the trapezoid parts, the shear deformation , the additional deformation caused by the elastic deformation of the base, and the contact deformation of the tooth surface meshed with the tooth surface.
The deformation of the gear tooth at the loading point without thermo-elastic coupling contacts can be derived by:
The deformation of the gear tooth associated with thermo-elastic coupling contacts can be derived by:
where subscript are expressed as the deformation associated with thermo-elastic coupled contacts. is the heat deformation caused by temperature field.
The deformation in traditional calculation method is elastic deformation based on material mechanics. The coupling method of elastic deformation and heat deformation is taken into account when considering the thermo-elastic coupling contact.
3. Simulations
Taking a pair of standard meshing spur gears as the research object, the static transmission errors based on thermo-elastic coupling are analyzed. The gear parameters of the calculation model are shown in Table 1, and the material performance parameters of the calculation model are shown in Table 2. Power 100 KW, speed 10000 r/min, gear accuracy grade 6, and excluding shaft, bearing and box deformation.
Through the finite element analysis, the static transmission errors of traditional method and the static transmission errors of the thermo-elastic coupling contacts of spur gears are shown in Fig. 1.
Table 1Parameter of gear
Tooth number | Pressure / (°) | Modulus / mm | Tooth thickness / mm | Modification coefficient / min |
23/51 | 25 | 3 | 20 | 0 |
Table 2Material parameter of gear
Material | Modulus of elasticity / GPa | Poisson ratio | Density / (kg·m-3) |
Low-carbon steel | 213 | 0.3 | 7820 |
Fig. 1STE of the example case
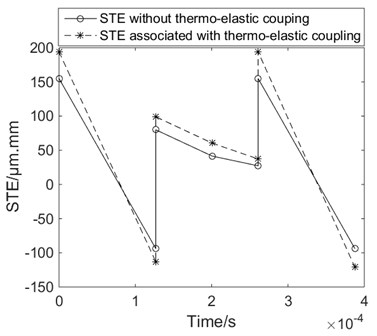
As shown in Fig. 1, it can be seen that the static transmission errors associated with thermo-elastic coupling contacts of spur gears pair is greater than the static transmission errors without thermo-elastic coupling contacts. This is because the high speed and heavy load gear generates large heat and the formed steady-state temperature high temperature in the field, causing heat deformations of spur gears [14].
4. Conclusions
The main work of this issue is as follows:
1) Calculation method of static transmission errors associated with thermo-elastic coupling contacts of spur gears is proposed.
2) The differences between STE without thermo-elastic coupling contacts and STE associated with thermo-elastic coupling contacts are obtained according to the simulation results of an example case of gear drives.
The method proposed in this paper considers the influxes of thermo-elastic coupling contacts compared with the traditional calculation method of STE. These contributions would benefit to improve gear drive modifications and engineering applications of gear drives in the future.
References
-
Song L. Design and Analysis of High Accuracy Testing for Gear Dynamic Transmission Error. Central South University, 2011.
-
Zhu X. Analysis of Load Capacity of Gears. Higher Education Press, Beijing, 1992.
-
Chen S., Tang J., Wu L. Dynamics analysis of a crowned gear transmission system with impact damping: Based on experimental transmission error. Mechanism and Machine Theory, Vol. 74, Issue 6, 2014, p. 354-369.
-
Hu Z., Tang J., Zhong J., et al. Frequency spectrum and vibration analysis of high speed gear-rotor system with tooth root crack considering transmission error excitation. Engineering Failure Analysis, Vol. 60, 2016, p. 405-441.
-
Inalpolat M., Handschuh M., Kahraman A. Influence of indexing errors on dynamic response of spur gear pairs. Mechanical Systems and Signal Processing, Vol. 60, Issue 61, 2015, p. 391-405.
-
Bodas A., Kahraman A. Guda-1 influence of carrier and gear manufacturing errors on the static planet load sharing behavior of planetary gear sets (gear unit design and applications). The Japan Society of Mechanical Engineers, 2017, p. 633-638.
-
Hotait M. A., Kahraman A. Experiments on the relationship between the dynamic transmission error and the dynamic stress factor of spur gear pairs. Mechanism and Machine Theory, Vol. 70, Issue 6, 2013, p. 116-128.
-
Wang Yuning, Sun Zhili, Du Yongying. A study on the contact characteristics of gear thermo-elastic coupling based on response surface and Monte Carlo method. Machinery and Electronics, 2014, p. 6-10.
-
Taburdagitan M., Akkok M. Determination of surface temperature rise with thermo-elastic analysis of spur gears. Wear, Vol. 261, Issue 5, 2006, p. 656-665.
-
Zhu C. C., Lu B., Xu X. Y., et al. Analysis of heavy duty marine gearbox with thermoelastic coupling. Journal of Ship Mechanics, Vol. 15, Issue 8, 2011, p. 898-905.
-
Shaobin L. Study on Coupled Thermo-Elastic Deformation and Nonlinear Dynamic Emulate about High-Speed, Heavy-Load Gear Transmission System. Chongqing University, 2004.
-
Yanyan S. Study on Coupled Accessory Gearbox Reliability Based on Thermal Analysis. Northeastern University, 2009.
-
Li Z., Zhu R. Sensitivity predictions of geometric parameters on engagement impacts of face gear drives. Journal of Vibroengineering, Vol. 17, Issue 5, 2015, p. 2236-2246.
-
Lixin Y. Thermo-elastic coupling stress reliability sensitivity analysis of meshing gear tooth. Journal of Mechanical Strength, Vol. 2, 2015, p. 295-299.
About this article
The authors are grateful for the financial support provided by the National Natural Science Foundation of China under No. 51775264. In addition, the authors declare that there is no conflict of interests regarding the publication of this article.
