Rupture stress of eutectic composite ceramics with rod-shaped crystals

Yu, Jinfeng; Ni, Xinhua; Liu, Xiequan; Du, Zhihong; Xu, Da

doi:10.21595/vp.2018.19878

Vibroengineering Procedia

Browse Procedia

Published: 19 October 2018

Check for updates

Rupture stress of eutectic composite ceramics with rod-shaped crystals

Jinfeng Yu¹

Xinhua Ni²

Xiequan Liu³

Zhihong Du⁴

Da Xu⁵

^{1, 2, 3, 4}Army Engineering University, Shijiazhuang, China

^{2, 3}Army Infantry College, Nanchang, China

⁵71901 Troops of PLA, Liaocheng, China

Corresponding Author:

Xinhua Ni

Cite the article Download PDF

Downloads 1219

Abstract

Eutectic composite ceramics has a wide range of applications in the aerospace industry due to its excellent mechanical properties. The rupture stress of the materials is a subject of considerable importance. Eutectic composite ceramics primarily consist of rod-shaped crystals, with a small amount of particles and preexisting defects dispersed throughout. Aligned nano-micron fibers are embedded within the rod-shaped crystals. Rupture stress of a eutectic composite ceramic depends on its fracture surface energy and preexisting defects. In this study, the equivalent fracture surface energy of a eutectic ceramic composite was calculated based on its additional fracture work. Next, the effects of the preexisting defects were considered. Then, a micromechanical model of the eutectic composite ceramic was established based on its microstructural characteristics. The defects were assumed to be lamellar, and the surrounding matrix was assumed to be transversely isotropic. Using this information, the rupture stress of the eutectic ceramic composite was predicted. A comparison of the theoretical and experimental results indicated that the predicted rupture stresses corresponded with the tested data.

1. Introduction

Eutectic composite ceramics have been increasingly used due to their excellent mechanical and functional characteristics. The rupture stress of a material, an important mechanical index, greatly limits its applications. The rupture stress of a material is dependent on numerous factors, particularly its micro-structural characteristics and defects. Eutectic composites ceramics are primarily comprised of rod-shaped crystals formed via combustion synthesis. Aligned nano-micro fibers are embedded within the rod-shaped crystals [1]. Previous experiments have shown that these cracks are propagated along the rod-shaped crystals through deflection. A method of preventing these rod-shaped grains has not yet been developed. As applied stress increases, inter-facial debonding inevitably occurs through micro-cracking along the boundaries of rod-shaped crystals, resulting in pull-out work. The pull-out work increases the fracture surface energy of the composite.

Sizes of defects and micro-structures exhibit nearly identical orders of magnitude, and, in some types of eutectic composite ceramics, the matrices surrounding defects is anisotropic. Therefore, crack tip stress fields and rupture mechanisms of defects in anisotropic matrices are complex. Despite these complications, considerable progress has been made in research. Sih [2] and Willis [3] developed a way to obtain the crack tip stress fields and stress intensity factors of matrices, providing a basic method for studying the fracture mechanisms of anisotropic materials. The prediction model of eutectic composite ceramics with rod-shaped crystals was built by Liu [4]. This study provided excellent resources concerning the rupture stress of eutectic composite.

The rupture stress of eutectic composite primarily depends on two factors: fracture surface energy and preexisting defects. In this study, the equivalent fracture surface energy of a eutectic ceramic composite was calculated based on its additional fracture work. Then, the effects of preexisting defects on the rupture stress were considered. In considerably-sized defects, the effects of lamellar defects are much greater than the effects of spheroidal defects. Thus, only lamellar defects were analyzed in this article. Based on the microstructures of eutectic composites, the defects were simplified as elliptical cracks in an anisotropic matrix. Then, a model of the rupture stress was established and information regarding the effects of defects were obtained based on eigenstrain theory and Griffith’s fracture criterion.

2. Equivalent fracture surface energy

Eutectic composite ceramics are primarily comprised of rod-shaped crystals containing nano-micron fibers, with a small amount of particles distributed throughout, as shown in Fig. 1. Since the propagation directions of cracks are different from the growth orientations of rod-shaped crystals, cracks are forced to bypass rod-shaped crystals, resulting in the formation of crack-bridging by the rod-shaped crystal in the wake of the crack tip. This crack-bridging results in bridging toughening. As applied stress increases, interfacial debonding inevitably occurs via micro-cracking along the boundaries of rod-shaped crystals, resulting in pull-out. Due to the high volume fraction of rod-shaped crystals in ceramics, the contribution of crack-bridging to toughening and the pull-out of rod-shaped crystals is considered to play a predominant role in ceramic toughening.

Fig. 1SEM microstructures of the ceramic composites, primarily comprised of rod-shaped crystals

When thermal residual stresses are present, rod-shaped crystal pull-out work can be appreciable. Residual stresses manifest as clamping forces between rod-shaped crystals. These forces accumulate during final crystal separation. Additional fracture work is used to define this work during separation.

Fig. 2Pull-out of a rod-shaped crystal bridging a crack plane

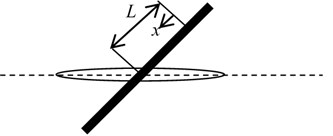
Additional fracture work can be calculated based on its origination from a frictional clamping force. Consider a rod-shaped crystal of radius $R$ that is pulled from a mating surface across the fracture plane (Fig. 2). The pull-out work is given by the integral of the frictional force divded by the pull-out length, $s$ . The frictional stress is represented by $τ$ . The area over which this stress operates is expressed as 2 $π R s$ where $s$ is the instantaneous distance over which the eutectic is clamped. This length varies with the extent of pull-out. Initially, the value of $s$ is represented by $s_{0}$ (slip length), but then decreases with the pull-out distance, represented by $s = s_{0} - x$ . Thus, pull-out work can be expressed as:

1

W = \int_{0}^{s_{0}} τ 2 π R (s_{0} - x) d x = τ π R s_{0}^{2} .

In this equation, the frictional stress is equal to $μ σ_{22}^{(0)}$ , where $μ$ represents the frictional coefficient, and $σ_{22}^{(0)}$ represents the transverse residual compressive stress of a rod-shaped crystal determined by Liu et al. 2009 [5]. In addition, the dissociated length is associated with the position of the main crack. When the main crack is located near the rod-shaped crystal, the dissociated length of its boundary will be approximately zero. When the main crack is located in the middle, the dissociated length will be approximately $s_{0} / 2$ . Thus, the average length of dissociation is approximately $s_{0} / 4$ , and the work of frictional force can be computed as:

2

W = \frac{1}{16} μ_{s} π R s_{0}^{2} σ_{22}^{(0)},

where $π R^{2}$ represents the cross-sectional area of the rod-shaped crystal. By defining the volume fraction of the rod-shaped crystals as $f_{f}$ , the dissociated work per unit area can be obtained using Eq. (2):

3

Δ J = \frac{1}{16 R} f_{f} μ l_{0}^{2} σ_{22}^{(0)} .

As shown in Eq. (3), as the slip length increases, the dissociated work of the rod-shaped crystal also increases. Thus, larger slip lengths are necessary to produce large amounts of more additional fracture work in a rod-shaped crystal. However, slip length is limited by certain conditions, and only a relatively weak connection interface can possess a large slip length. The experimental results indicated that micro-slips would be observed in the weak interface of a rod-shaped crystal under loading. Once reaching a certain value, the slips resulted in micro-interface debonding. As the load increased, the micro-interface debonding was further dissociated. Thus, the additional fracture work increased with the slip length and interface frictional shear stress.

Furthermore, the slip length should increase with the critical length ( $l_{c}$ ) since both are dependent on bond strength. When a rod-shaped crystal is long, $l > l_{c}$ , where $l$ is the length of the rod-shaped crystal. By assuming that $s_{0} = l_{c}$ , $l_{c}$ is expressed as follow:

4

l_{c} = \frac{D σ_{f u}}{2 τ} = \frac{D σ_{f u}}{2 μ σ_{22}^{(0)}} .

Here $σ_{d u}$ is the breaking stress of a rod-shaped crystal as determined by Ni et al. 2014 [6]. We obtain:

5

Δ J = \frac{1}{16} \frac{f_{f} R σ_{d u}^{2}}{μ σ_{22}^{(0)}} .

When the lengths of rod-shaped crystals are less than the critical length, bridging still contributes to fracture work. Under these conditions, the average pull-out length is likely to be on the order of $l / 4$ . By substituting $l$ for $s_{0}$ in Eq. (5), the additional fracture work per unit area can be obtained.

The toughness of a eutectic composite ceramic can be expressed as $J C = J m + ∆ J$ , where Jm represents the toughness of the matrix in a rod-shaped crystal. Like the surface energy work, the fracture work scales linearly with crack length. The material toughness is defined as 2 $γ$ , where $γ$ is the fracture surface energy of the material. Thus, the toughness of the eutectic composite ceramic can be expressed as $2 γ = 2 γ m + ∆ J$ , where $γ m$ is the fracture surface energy of the matrix in a rod-shaped crystal, and its equivalent fracture surface energy can be described as:

6

γ = γ_{m} + Δ J / 2 .

Bridging greatly affects the toughening of eutectic composite ceramics. Crack bridging leads to intergranular put-out work. This effect is usually incorporated into the measured fracture surface energies of materials.

3. The rupture stress

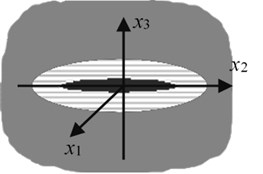
Eutectic composites primarily consist of rod-shaped crystals, with particles and small defects dispersed throughout. Consider a eutectic composite with defects consisting of three-phase cells randomly and spatially distributed with an appropriate matrix volume fraction of matrix. All of these cells have the same shape and can be embedded into the equivalent medium shown in Fig. 3. In the three-phase cell, the effective matrix surrounding an elliptical defect consists of uniformly-distributed rod-shaped crystals and is transversely isotropic (where $x_{1}$ and $x_{3}$ comprise the basal planes), and the ellipsoid defect is defined as ${(X / a_{1})}^{2} + {(Y / a_{2})}^{2} + {(Z / a_{3})}^{2} \leq$ 1, where $a_{3} ≪ a_{1}$ , and $a_{2}$ is perpendicular to the rod-shaped crystal. Let $σ^{D}$ be the effective applied stress at infinity. The boundary conditions on the crack surface are equal to:

7

σ_{3 j}^{D} + σ_{3 j} = 0, j = 1,2, 3,

where $σ_{3 j}$ is the stress disturbance resulting from the crack. This stress disturbance can be simulated by the eigenstress derived from an equivalent ellipsoidal inclusion with eigenstrain $ε^{*}$ as [7].

Fig. 3Three-phase model of a defect

8

σ_{i j} = C_{i j k l}^{0} [\frac{a_{1} a_{2} a_{3}}{4 π} C_{p q m n}^{0} ε_{m n}^{*} \int_{S^{2}}^{} G_{k p l q} (x) u^{- 3} d S (x) - ε_{k l}^{*}],

where $C_{p q m n}^{0}$ is a corresponding component of the fourth-order stiffness tensor of the matrix. $u = {(a_{1}^{2} x_{1}^{2} + a_{2}^{2} x_{2}^{2} + a_{3}^{2} x_{3}^{2})}^{1 / 2}$ , $G_{k p l q} (x) = x_{l} x_{q} K_{k p}^{- 1}$ , $K_{k p} = C_{p q m n}^{0} x_{i} x_{j}$ . Using the following variable substitutions:

9

x_{1} = \sqrt{1 - t {}^{2}} c o s θ, x_{2} = \sqrt{1 - t {}^{2}} s i n θ, x_{3} = t .

$G_{k p l q}$ can be expressed as $G_{k p l q} (θ, t) = G_{k p l q} [\sqrt{1 - x_{3}^{3}} c o s θ, \sqrt{1 - x_{3}^{3}} s i n θ, x_{3}]$ , and $d S (x) = d x_{3} d θ = {(1 - x_{3}^{2})}^{3 / 2} d θ$ . Thus:

10

\int_{S^{2}} G_{k p l q} (x) u^{- 3} d S (x) = \int_{0}^{2 π} \frac{d θ}{a_{1}^{2} a_{2}^{2} a_{3}^{2}} \int_{- \infty}^{\infty} \frac{G_{k p l q} (c o s θ, s i n θ, t)}{(c o s^{2} θ / a_{2}^{2} a_{3}^{2} + s i n^{2} θ / a_{1}^{2} a_{3}^{2} + t^{2} / a_{1}^{2} a_{2}^{2})^{3 / 2}} d t,

and Eq. (8) can be simplified as:

11

σ_{i j} = \frac{1}{4 π} C_{i j k l}^{0} C_{p q m n}^{0} ε_{m n}^{*} [4 π G_{k p l q} (0,0, 1) - a_{3} Π_{k p l q}] - C_{i j k l}^{0} ε_{m n}^{*} = \frac{1}{4 π} a_{3} C_{i j k l}^{0} C_{p q m n}^{0} ε_{m n}^{*} Π_{k p l q} .

As $a_{3} \to$ 0, by substituting Eq. (11) into Eq. (7), we can obtainand:

12

σ_{3 j}^{D} + a_{3} L_{i j m n} ε_{m n}^{*} = 0,

where $L_{i j m n} = - \frac{1}{4 π} C_{i j k l}^{0} C_{p q m n}^{0} Π_{k p l q}$ and the interaction energy can be expressed as:

13

Δ W = - \frac{1}{2} \frac{4 π}{3} a_{1} a_{2} a_{3} σ_{D} ε^{*} = - \frac{2 π}{3} a_{1} a_{2} σ_{3 j}^{D} a_{3} ε_{3 j}^{*} .

Assume that the defects propagate self-similarly. Then the Griffith fracture criterion is equal to:

14

δ J = 0 J = Δ W + 2 π a_{1} a_{2} γ,

where $γ$ is the fracture surface energy of the material. By substituting Eqs. (13) into Eq. (14), we can obtain:

15

[γ - \frac{(σ_{33}^{D})^{2} P_{3333}}{L_{3333}^{2}} - \frac{(σ_{32}^{D})^{2} P_{3232}}{L_{3232}^{2}} - \frac{(σ_{31}^{D})^{2} P_{3131}}{L_{3131}^{2}}] \frac{δ a_{1}}{a_{1}} = 0,

or:

16

[γ - \frac{(σ_{33}^{D})^{2} Q_{3333}}{L_{3333}^{2}} - \frac{(σ_{32}^{D})^{2} Q_{3232}}{L_{3232}^{2}} - \frac{(σ_{31}^{D})^{2} Q_{3131}}{L_{3131}^{2}}] \frac{δ a_{2}}{a_{2}} = 0 .

Thus, the rupture stress can be expressed as:

17

σ_{c}^{} = {(\frac{γ}{\frac{B_{33}^{2} P_{3333}}{L_{3333}^{2}} + \frac{B_{32}^{2} P_{3232}}{L_{3232}^{2}} + \frac{B_{31}^{2} P_{3131}}{L_{3131}^{2}}})}^{\frac{1}{2}}, σ_{c}^{} = {(\frac{γ}{\frac{B_{33}^{2} Q_{3333}}{L_{3333}^{2}} + \frac{B_{32}^{2} Q_{3232}}{L_{3232}^{2}} + \frac{B_{31}^{2} Q_{3131}}{L_{3131}^{2}}})}^{\frac{1}{2}} .

Here:

P_{i j m n} = \frac{a_{1} a_{2}}{4 π} C_{i j k l}^{0} C_{p q m n}^{0} \cdot \int_{0}^{2 π} d θ \int_{- 1}^{1} \frac{a_{1}^{2} c o s^{2} θ}{(a_{1}^{2} c o s^{2} θ + a_{2}^{2} s i n^{2} θ)^{5 / 2}} \frac{x_{3}^{}}{(1 - x_{3}^{2})^{1 / 2}} \frac{\partial G_{k p l q} (x_{1}^{}, x_{2}^{}, x_{3}^{})}{\partial x_{3}^{}} d t,

Q_{i j m n} = \frac{a_{1} a_{2}}{4 π} C_{i j k l}^{0} C_{p q m n}^{0} \cdot \int_{0}^{2 π} d θ \int_{- 1}^{1} \frac{a_{1}^{2} s i n^{2} θ}{(a_{1}^{2} c o s^{2} θ + a_{2}^{2} s i n^{2} θ)^{5 / 2}} \frac{x_{3}^{}}{(1 - x_{3}^{2})^{1 / 2}} \frac{\partial G_{k p l q} (x_{1}^{}, x_{2}^{}, x_{3}^{})}{\partial x_{3}^{}} d t .

Each component $C_{i j k l}^{0}$ for the stiffness tensor of matrix composed of rod-shaped crystals can be determined by Li et al 2011[8].

The Al₂O₃/ZrO₂ ceramic composites were obtained through a eutectic reaction under a high degree of undercooling. The samples were cut and grounded into rectangular bars measuring 3 mm (width)×4 mm (height)×36 mm (length) in order to determine their rupture stress.

Table 1Comparison of the theoretical and experimental results

Material number	Defects volume fraction $f_{p}$ (%)	Defects average diameter $a$ / μm	(experimental data) Rupture stress $σ_{c u}$ / MPa	(theoretical result) Rupture stress $σ_{c u}$ / MPa
1	0.2	0.7	1568	1868
2	0.8	0.8	1278	1774
3	1.2	2.4	1256	1636
4	2.8	1.1	1050	1115
5	3.7	2.3	800	973
6	8.5	1.9	680	768

The experimental rupture stress data was measured using a three-point bending method with a cross-head speed of 0.5 mm/min and a span of 30 mm. The volume fractions and average diameters of the defects were determined using the linear intercept method on an SEM photograph. The theoretical rupture stresses were calculated using Eq. (17). The comparison between the theoretical and tested results is shown in Table 1. The predicted rupture stresses corresponded with the tested data.

4. Conclusions

The rupture stress of the eutectic composite ceramic was determined using its fracture surface energy and preexisting defects. The equivalent fracture surface energy of the eutectic ceramic composite was computed based on its additional fracture work. The microstructure model was established based on the characteristics of eutectic composite materials with preexisting defects. Assuming a material is completely brittle, its rupture stress model containing its lamellar defects was obtained using Griffith's fracture theory. The material was assumed to be completely brittle for simplification, and the results were less than the experimental values.

References

Zhao Z. M., Zhang L., Song Y. G., et al. Microstructures and properties of rapidly solidified Y₂O₃ doped Al₂O₃/ZrO₂ composites prepared by combustion synthesis. Scripta Materialia, Vol. 55, 2006, p. 819-822.

Search CrossRef
Sih G. C., Leibowitz H. Mathematical Theories of Brittle Fracture. Academic Press, New York, 1968.

Search CrossRef
Willis L. J. The stress field of an elliptical crack in anisotropic medium. International Journal of Engineering Science, Vol. 6, 1968, p. 253-263.

Publisher
Liu X. Q., Chen C., Ni X. H. Strength prediction model of eutectic composite ceramics mainly composed of rod-shaped crystals. Vibroengineering Procedia, Vol. 2, 2013, p. 2345-533.

Search CrossRef
Liu X. Q., Ni X. H., Cheng Z. G., et al. Size dependent residual stress field of composite ceramic with eutectic interphases. Transferability and Applicability of Current Mechanics Approaches, Chengdu, 2009.

Search CrossRef
Ni X. H., Chen C., Zhang S. Q. Fracture toughness prediction of eutectic ceramic composite considering damage effect and transformation toughening. Journal of Vibroengineering, Vol. 16, 2014, p. 1510-1522.

Search CrossRef
Huang H. J., Liu S. K. On a flat ellipsoidal inclusion or crack in three-dimensional anisotropic media. International Journal of Engineering Science, Vol. 36, 1998, p. 143-155.

Publisher
Li B. F., Zheng J., Ni X. H., et al. Effective elastic constants of fiber-eutectics and transformation particles composite ceramic. Advanced Materials Research, Vol. 177, 2011, p. 182-185.

Publisher

About this article

Received

09 April 2018

Accepted

19 May 2018

Published

19 October 2018

SUBJECTS

Mathematical models in engineering

DOI

https://doi.org/10.21595/vp.2018.19878

Keywords

eutectic composite ceramic

rupture stress

preexisting defects

micromechanical model

Acknowledgements

This material is based upon work supported by the National Natural Science Foundation of China under Grant No. 11272355.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2022 02 05

Effect of defect distribution on thermal expansion coefficient of eutectic composite ceramics

Zhihong Du, Runxiu Yang, Mian Wu

Research article

2022 02 05

Research on the heat transfer and internal residual stress of multi-phase systems

Mingjie Li, Xiaoming Lv, Youbang Wu

Research article

2020 11 26

Fracture and damage model of composite ceramics

Jinfeng Yu, Zhaogang Cheng, Xinhua Ni, Xiequan Liu, Da Xu

Research article

2019 03 15

Numerical investigation for influence of pre-twist on stress behavioral characteristics of curved blade

Pavan Kishore Mamaduri, Chandra Sekhar Akula, Himam Saheb Shaik

J. Yu, X. Ni, X. Liu, Z. Du, and D. Xu, “Rupture stress of eutectic composite ceramics with rod-shaped crystals,” Vibroengineering PROCEDIA, Vol. 20, pp. 231–236, Oct. 2018, https://doi.org/10.21595/vp.2018.19878

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2018.19878
UR  - https://doi.org/10.21595/vp.2018.19878
TI  - Rupture stress of eutectic composite ceramics with rod-shaped crystals
T2  - Vibroengineering PROCEDIA
AU  - Ni, Xinhua
AU  - Yu, Jinfeng
AU  - Liu, Xiequan
AU  - Du, Zhihong
AU  - Xu, Da
PY  - 2018
DA  - 2018/10/19
PB  - JVE International Ltd.
SP  - 231-236
VL  - 20
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Ni_2018,
	doi = {10.21595/vp.2018.19878},
	url = {https://doi.org/10.21595/vp.2018.19878},
	year = 2018,
	month = {oct},
	publisher = {{JVE} International Ltd.},
	volume = {20},
	pages = {231--236},
	author = {Xinhua Ni and Jinfeng Yu and Xiequan Liu and Zhihong Du and Da Xu},
	title = {Rupture stress of eutectic composite ceramics with rod-shaped crystals},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]X. Ni, J. Yu, X. Liu, Z. Du, and D. Xu, “Rupture stress of eutectic composite ceramics with rod-shaped crystals,” Vibroengineering PROCEDIA, vol. 20, pp. 231–236, Oct. 2018, doi: 10.21595/vp.2018.19878.

Copy IEEE

Copied to clipboard!

Ni, Xinhua, Jinfeng Yu, Xiequan Liu, Zhihong Du, and Da Xu. “Rupture Stress of Eutectic Composite Ceramics with Rod-Shaped Crystals.” Vibroengineering PROCEDIA 20 (October 19, 2018): 231–36. https://doi.org/10.21595/vp.2018.19878.

Copy Chicago

Copied to clipboard!

Rupture stress of eutectic composite ceramics with rod-shaped crystals

Abstract

1. Introduction

2. Equivalent fracture surface energy

3. The rupture stress

4. Conclusions

References

About this article

Related Articles