Fracture and damage model of composite ceramics

1. Introduction

Eutectic composite ceramics have excellent mechanical properties such as high temperature resistance, high strength, high hardness and corrosion resistance, which has very important application value in the field of ceramic armor and aerospace. Therefore, the research on the damage and fracture behavior and failure mechanism of eutectic composite ceramics has attracted a large number of material scientists and scholars Mechanical workers pay more attention to it. Especially when the eutectic structure of composite ceramics is triangular symmetry structure, the ceramic materials have higher room temperature and high temperature mechanical properties, the lowest high temperature creep and the highest room temperature fracture toughness due to the high melting enthalpy of eutectic two phases and the stability of triangular symmetry. Obviously, the damage and fracture behavior of the composite ceramics is closely related to the microstructure of the material.

In recent years, for the study of mechanical properties of composite ceramics, the relationship between the microstructure of different materials and the macro mechanical properties of materials has been established [1-3]. For example, based on shear lag theory, mesostructure and interface properties, the initial tensile modulus of the material is predicted, and the strength model and damage constitutive relationship of 2D-C/SiC composites are established [4-6]. Based on the meso structure of fiber reinforced ceramic matrix composites, a micromechanical model of bridged fiber was established. Considering the influence of interface, the tensile modulus of the material was predicted, and the influence of interfacial bonding strength on the fracture strength of the material was analyzed [7]. According to the microstructure of the rod eutectic containing parallel reinforcing fibers, the damage fracture stress of the rod eutectic containing parallel fibers is determined based on the microscopic damage in the eutectic [8]. The cohesive bond fracture condition between two phases of eutectic is not considered in the above model. Based on the triangular symmetry structure of eutectic clusters, the limit stress of the composite ceramics was predicted [9]. Based on the microstructure characteristics of eutectic ceramics containing parallel fibers, a damage fracture model of parallel fiber eutectic composite ceramics was established [10]. These studies lay a foundation for the analysis of the damage and fracture of trigonometrically symmetric eutectic multiphase ceramics.

Compared with the general micromechanics, the study of material fracture from the perspective of bonding bond can provide more profound physical understanding. The earliest bond fracture model is Orowan [11] and Gilman [12], which describes the bond failure in turn in the process of brittle fracture by using the function of interatomic cohesion. With the development of computing technology, cohesive fracture model has been further developed. Du Zhihong [13] combined cohesive fracture model with adaptive mesh to describe the propagation process of multiple cracks along free paths. Ni Xinhua [14] used the exponential cohesive fracture model to describe the separation process of materials. Zhou Fenghua and Wang Lili [15] used the linear cohesive fracture model to describe the expansion behavior of the virtual fracture point. However, these models study the bond fracture of single-phase materials, and for composite ceramics with eutectic properties, it is necessary to improve these models.

According to the damage degree, the macro crack tip field can be divided into non-destructive zone, continuous damage zone and damage localization zone, and the most serious damage area is damage localization zone. It is the basis of analyzing the crack tip field of multiphase ceramics, and is also the prerequisite to determine whether the macro crack propagation of multiphase ceramics can be unstable. According to the meso damage theory of crack tip, microcracks grow steadily in the continuous damage zone at the crack tip, and then the microcracks will enter the damage localization zone where stress drop occurs and continue to expand. The nonlinear damage section is introduced into the shielding effect analysis of crack tip in reference [16]. It is proved that the stress distribution in the damage saturation region is still K field, and the stress drop and strain softening play a major role in the smaller range of crack tip.

According to the microstructure of the composite ceramics, considering the effect of micro damage on the effective properties of the composite ceramics, a two-scale cellular model is established to analyze the cohesive bond fracture conditions, and the micro damage fracture stress model is established the length of localized band of end damage was predicted.

2. Two scale cellular model

The composite ceramics are mainly composed of triangular symmetric eutectic. The eutectic body contains nanofibers. According to the microstructure characteristics of eutectic based multiphase ceramics, a two scale cellular model is established, as shown in Fig. 1.

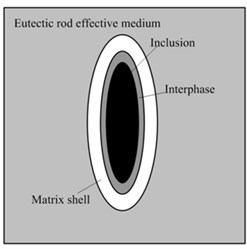
One is that the rod-shaped eutectic with triangular symmetric eutectic is arranged in the same direction, forming an ellipsoid like structure in the local area. This ellipsoid is placed in the matrix of particle structure and randomly distributed in space to form eutectic multiphase ceramics, forming a two-scale cellular model of the material. The other is that the ZrO₂ reinforced phase is uniformly distributed in the Al₂O₃ matrix in a single eutectic, forming rod-shaped eutectic. The eutectic consists of micro cell and effective medium, as shown in Fig. 2.

3. Fracture stress of polymer bond in eutectic

It is assumed that cohesive bond fracture occurs in eutectic. At the phase boundary of eutectic, the fracture stress of two-phase cohesive bond is the same, and the functional relationship between bond bonding stress and separation displacement can be expressed by half sine function:

where, ${\delta }_{th}$ is the cohesive bond fracture stress of eutectic, ${\delta \text{'}}_i$ is the bond range parameter, $i=$0 represents the matrix phase, $i=b$ represents the reinforced phase. Because the matrix and reinforcement share the same bond, the slope of bond stress curve at the equilibrium point should be equal to its elastic modulus:

where $b_0$ is the equilibrium atomic spacing. If the stress is interrupted at $2u=\delta \text{'}$, and the integral of the bond bond stress function to the displacement is equal to the surface energy ${\gamma }_i$, then:

Fig. 1Two scale cell model of eutectic with symmetrical triangular reinforced fibers

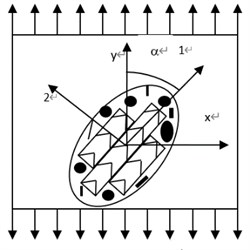
Fig. 2Microcosmic cell and effective medium

According to Eqs. (2) and (3), the cohesive bond fracture stress of eutectic is obtained as follows:

It can be seen from the above formula that the cohesive bond fracture stress of triangular symmetric eutectic is related to the elastic modulus, surface energy of fiber reinforced phase and matrix in the eutectic body, and the bonding bond arrangement mode shared by the eutectic two phases.

4. Fracture stress model of eutectic micro damage

Because in the eutectic body, the fibers in the same triangle area are arranged in the same direction and parallel, as follows:

where $l$ and $d$ are the length and diameter of the fiber respectively, $n$ is the dimensionless quantities.

At the junction of eutectic two phases, there is a large stress concentration due to dislocation accumulation, and a stress field will be generated around it. The maximum tensile stress produced by this stress field:

From Eqs. (4), (5) and (6), it can be concluded that the damage fracture stress of reinforced fiber eutectic with triangular symmetry distribution is:

Among them, ${\left(E_{11}^g\right)}^{\text{'}}=f(E_{11},E_{22},{\mu }_{12},d_1,d_2,d_3)$, ${E\text{'}}_{22}^{}=\left(1-d_2\right)E_{22}^{}$, $E_{11}$ and $E_{22}$ are the longitudinal and transverse elastic modulus of a triangle region in the eutectic group, and $d_1$, $d_2$ and $d_3$ are the microscopic damage variables in the three directions of longitudinal, transverse and shear respectively.

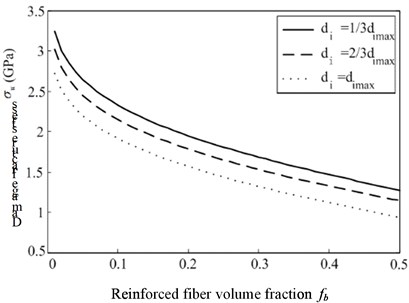
Taking Al₂O₃-ZrO₂ triangle symmetric eutectic group based composite ceramics prepared by high gravity method as an example. The material constants of matrix and fiber inclusion are as follows: $E_0=$402 GPa, ${\nu }_0=$0.233, ${\gamma }_0=$1.06 J.m^-2, $E_b=$233 GPa, ${\upsilon }_b=$0.31, ${\gamma }_b=$1.829 J.m^-2,respectively. The length of reinforcing fiber is $l_b=$ 2 µm, fiber diameter $d=$ 200 nm and damage variable $d_i=d_{imax}$ ($i=$1, 2, 3). According to the Eq. (7), the curve of the microcosmic damage fracture stress with the diameter of the reinforced fiber is obtained, as shown in Fig. 3.

Fig. 3Schematic representation of the variation of damage fracture stress with reinforced fiber volume fraction

5. Damage localization band of multiphase ceramics

The model of the damage localization was established (Fig. 4) based on the underlying theory of the Dugdale-Barenblatt model. The coordinate system $oxy$ is built on the tip of the damage localization band, supposing the length of this band is $l$, and $a$ is the radius of the microcrack. The length is related to the far-field stress intensity factor $K_{\infty }$ and $l\ll a$.

Under the tensile stress ${\sigma }_{\infty }$, the stress intensity factor is obtained as follows:

where $c=l+a$. The distribution of the normal stress in the extension line along the $y$ direction is given by the following:

where $r=x$ is the distance between the crack tip and the end of the damage localization band, $0\le r\le l$.

Assume that the stress distribution lies in $-l\le x\le 0$ is:

These conditions are reasonable because the size of the damage localization band was very small compared with the crack size, namely, $l\ll a$. Furthermore, only the stress of the points close to the band was of concern. Thus, $r\ll c$. When one pair of concentrated forces $\tilde{\sigma }\left(\xi \right)d\xi$ focus on the point of $x=\xi$ ($\xi <0$), the normal stress along the $y$ axis around the damage localization band is expressed as follows:

The corresponding stress intensity factor is:

For a microcell with reinforced lamella eutectic, when the stress is linearly distributed in the damage localization band, the stress is given by:

Assuming that the residual strength is the damage fracture stress of lossy eutectic with linear distribution, Eq. (7) is substituted into Eq. (13) to obtain:

The length of the damage localization zone is obtained:

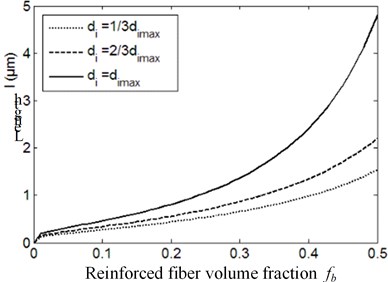
Take the diameter of reinforcing fiber as $d=$ 200 nm. Assuming the far-field stress intensity factor of triangular symmetric eutectic matrix composite ceramics $K_{\infty }=$ 5 MPa⋅m^1/2, the change curve between the length of damage localization band and the volume fraction of reinforcement phase can be obtained from Eq. (15), as shown in Fig. 5.

It can be seen from Fig. 5 that with the increase of the volume fraction of the reinforced fiber, the length of the damage localization band becomes longer, the higher the damage degree, the smaller the residual strength, and the longer the length of the damage localization band. The maximum length is $l_{max}=$4.8 µm.

Fig. 4Model of damage localization band at crack tip

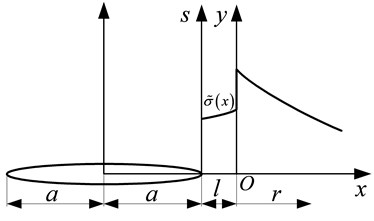
Fig. 5Relationship between the length of damage localization band and reinforced fiber volume fraction

6. Conclusions

The damage fracture stress of the eutectic with triangular symmetric reinforced fiber is related to the meso parameters and damage degree of the material. It decreases with the increase of the volume fraction of the reinforced fiber, and decreases with the increase of the damage variable. The quantitative analysis shows that with the increase of fiber volume fraction, the strong confinement of interfacial phase is destroyed, the residual strength decreases and the length of damage localization band increases with the increase of fiber volume fraction. Reducing the damage degree as much as possible and selecting the appropriate fiber volume content can increase the fracture stress of eutectic, and then reduce the length of damage localization band, improve the threshold value of crack propagation instability, and enhance the material strength.