Research on interface slippage of fiber reinforced composite ceramics

1. Introduction

The fiber-reinforced composite ceramics whose main structure is triangular symmetrical eutectic have good mechanical properties under high temperature and normal temperature conditions[1]. When the fibers in the eutectic cluster are distributed triangular symmetrically, the strong confinement property and the trigonal symmetry stable structure of the nanoscopic interface between fiber and matrix make composite ceramics have excellent anti-high-temperature creep. And the local slip feature of the micro-interface between eutectic groups makes it have high fracture toughness[2]. Many literatures have analyzed micromechanics about the strong constraining characteristics of the nano-interface, such as the microscopic stress field of unidirectional jagged inclusion eutectics[3], the damage strain field of unidirectional parallel eutectics[4], and damage intensity model of composite ceramics with damaged eutectics[5] etc. In order to reveal the relationship between the mechanical properties and the microstructure of the composite ceramic whose main structure is triangular symmetrical eutectic, the influence which the local slip property of the micro-interface between eutectic clusters brings to the composite ceramic mechanical behavior must be further analyzed.

In order to reveal the relationship between the micro-interface slip and the macro-mechanical behavior of a two-scale interfacial composite ceramics with main structure of triangular symmetrical eutectic, this paper first determines the relationship between the line strain of the triangular symmetrical eutectic outside surface and the external load of the composite ceramic under the condition of the microscopic interface without slipping. And then calculating the maximum shear stress assumed of the triangular symmetry eutectic group based on the line strain on the outer surface of the eutectic group. Finally, the ultimate shear stress of the micro-interface of the composite ceramic is determined based on the hardness and toughness fracture of the composite ceramic measured by the indentation test. When the maximum shear stress that the outer surface of the eutectic group can bear reaches the ultimate shear stress of the micro-interface of the composite ceramic, the microscopic interface sliding stress in the composite ceramic is obtained.

2. Line strain of eutectic in fiber direction under external load

In order to link the stress in the triangular symmetry eutectic group with the external load, firstly the extra line strain that can be transmitted by the triangular symmetry eutectic is calculated before the microscopic interface slip, that is, when the composite ceramic only produces elastic deformation. The randomly oriented triangular symmetric eutectic clusters and their surrounding effective media were taken as the research object. The triangular region in the eutectic group is transversely isotropic and the surroundings are isotropic effective medium, as shown in Fig. 1. When the macro-coordinate system $o\xi \eta$ is established, the composite ceramic bears the tensile load $o$ along the macroscopic axis $\eta$, the triangular symmetric eutectic group can be regarded as the composite ceramic before the micro-interface between the eutectic groups is slipped. For a unit body, assuming that the angle between the axis of the eutectic group and the loading direction is $\alpha$, the line strain at the outer boundary of the eutectic group in the eutectic group’s micro-coordinate system is:

where ${\mathbf{\sigma }}_g$ is a eutectic outer micro stress field, ${\mathbf{\sigma }}_g=({\sigma }_{11},{\sigma }_{22},{\sigma }_{33},{\sigma }_{13},{\sigma }_{23},{\sigma }_{12}{)}^T$:

where, axis 1 is along the eutectic crystal direction, and the mesoscopic axes 2 and 3 are perpendicular to the mesoscopic axis 1. $\alpha$ is the angle between the axis 1 and the external load $\sigma$, the other components are all 0, so ${\mathbf{\sigma }}_g$ can be written as:

$\mathbf{S}$ is composite material equivalent flexibility matrix:

$E$ and $\upsilon$ are the elastic modulus and Poisson’s ratio of composite ceramics, which can be determined by the formula of [5].

Under the action of the external strain field ${\mathbf{\epsilon }}_{}^e$, the stress field in the eutectic is:

where:

where $C_{ijkl}^g$ is the stiffness tensor component of a triangular symmetric eutectic group in a micro-coordinate system which is determined by the formula [6].

Fig. 1The triangular symmetrical eutectic in the composite ceramic

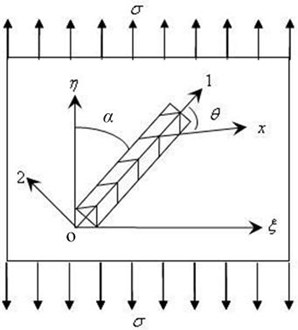
Set the nanometric coordinate axis of the parallel fiber inclusions in the triangular region is $x$ (nano-axial coordinate axis y which is perpendicular to the $x$ is omitted in the figure), and the angle of the $x$-axis and the crystal axis of the eutectic group (it is, the mesoscopic coordinate axis 1) is $\theta$, without loss of generality, it is considered that the coordinate axis $z$, the mesoscopic axis 3, and the macro axis are parallel. Take a part to analyze and assume its fiber axis is in the plane of the diagram, then the strain of the eutectic in the fiber direction in the nanoscopic coordinate system is:

In summary, under the condition of elastic deformation, the stress strain is always linear:

where:

$E_{xx}$ and ${\upsilon }_{xy}$ is the elastic modulus and Poisson’s ratios of the eutectic group along the fiber direction in the triangulation region are determined by the formula of [6]. Eq. (11) shows that the line strain along the fiber direction of the eutectic group under external load is not only related to the macroscopic elastic constant of the composite ceramic, the mesoscopic elastic constant of the eutectic and the nanoscopic elastic constant of the triangular region, but also the orientation of the eutectic group and the orientation of the fiber inclusions in the eutectic group.

3. Maximum shear stress borne by the eutectic

If a cylinder containing fibrous inclusions is taken in a triangular region of the eutectic group, the fiber inclusion and the radius of the cylinder are $r_0$ and $R$ respectively. If the coordinate origin of the nano coordinate axis $x$ is at the midpoint of the fiber inclusion and the fiber length is 2$L$, the equilibrium equation under the elastic deformation condition can be obtained according to:

where, ${\sigma }_f$ is normal stress on the fiber cross section, ${\tau }_f$ is the eutectic group in the interface between the matrix and fiber shear stress. The nanostructure of a triangular region of a eutectic group is similar to that of a eutectic containing parallel fibers. Under elastic deformation conditions, both the matrix and the fiber inclusion must satisfy Hooke’s law, and outermost matrix strain and the applied strains along the fiber direction in eutectic ${\epsilon }_x^e$ are equal. According to the boundary conditions where the eutectic group bears the shear stress, that is, there is no normal stress at the fiber inclusion end, the shear stress at the interface between the matrix and the fiber can be solved according to Eq. (12) [9]:

where, $k=\sqrt{\frac{2G_m}{\mathrm{l}\mathrm{n}\left(\pi /f_b\right)E_f}}$, $G_m$ is the matrix shear modulus, $f_b$ is the volume fraction of fiber inclusions, $E_f$ is the volume fraction of fiber inclusions. Substituting Eq. (11) into Eq. (13), and let $x=L$, the maximum shear stress that the eutectic can bear under external load and elastic deformation:

4. Microscopic interface slippage stress in composite ceramics

The interface between the eutectic clusters is a weak interface. Under the shear stress, there is countless dislocation blocked and plugged up. The tip of the dislocation plug-in group is the micro-crack tip. The length of the slip surface at the critical point of the indentation cracking is [9]:

In the formula, $H$ and $K_{IC}$ represent the hardness and fracture toughness of composite ceramics, which can be measured by indentation experiments. The critical shear stress on the slip surface during when crack nucleation is formed satisfies the following formula [9]:

In the formula, $\gamma$ and $\mu$ are the surface free energy and shear modulus of composite ceramics. Substituting Eq. (15) into Eq. (16), the ultimate shear stress bear by the micro-interface in the composite ceramic can be determined:

When the maximum shear stress on the eutectic surface is equal to the ultimate shear stress at the micro-interface of the composite ceramic, it is, ${\tau }_{max}={\tau }_{mu}$, the microscopic interface in the composite ceramic slips. According to Eqs. (14) and (17), the micro-interface slippage stress in composite ceramics can be obtained as:

In order to analyze the influence of the volume fraction and size of the fiber inclusions, the following quantitative studies are conducted on specific materials. For the double-scale interface composite ceramics mainly composed of Al₂O₃-ZrO₂ triangular symmetry eutectic groups prepared by the high-gravity combustion synthesis method, the angles between the fiber inclusions and the crystal axis are known from the eutectic crystal plane characteristics is $\theta =\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s}\frac{2\sqrt{3}}{\sqrt{13}}$. The material constants of the matrix and fiber inclusions are $E_m=$ 402 GPa, ${\upsilon }_m=$ 0.233; $E_f=$ 233 GPa, ${\upsilon }_f=$ 0.31, $f=$ 0.3, $l=$ 10 μm, $d=$ 300 nm. The macroscopic, mesoscopic and nanoscopic elastic constants of composite ceramics are determined by formulas of [7, 8]. Let $\alpha =$ 60°, fiber length $l=$ 10 μm, fiber volume fraction $f=$ 0.3, then the relationship between the slippage stress and the fiber diameter is shown in Fig. 2.

Fig. 2The relationship between slipping stress and fiber diameter of triangular symmetrical eutectic

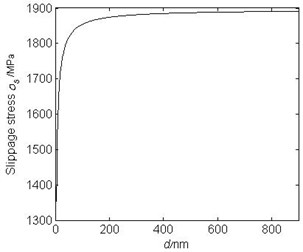
Fig. 3The relationship between slipping stress and fiber volume fraction of triangular symmetrical eutectic

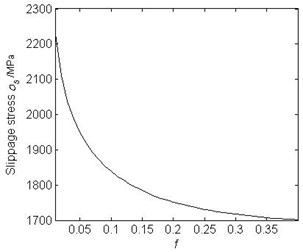
It can be seen from Fig. 2 that the slippage stress of the micro-interface in the composite ceramic increases with the increase of the fiber inclusion diameter, and the change rate is faster when the diameter is less than 100 nm. If other parameters are not changed and the fiber diameter $d$ is $d=$ 100 nm, the relationship between the slippage stress and the fiber volume fraction is shown in Fig. 3. The slippage stress of the composite ceramic decreases with the increase of the fiber volume fraction. The larger the fiber volume fraction, the easier the eutectic lumps to slip.

To test the micro failure mechanism proposed in this paper, some tested data is cited to check the theoretical results. The theoretical calculations and the experimental data of the strength of composite are shown in Table 1.

As shown in Table 1, the calculated strength of composite in this article is reasonable compared to the test data. All the calculated values are a little higher than the tested values. The anomalous cracks and pores in the crystal boundary may be the major reasons for this difference.

5. Conclusions

When the maximum shear stress on the outer surface of the triangular symmetric eutectic group is equal to the ultimate shear stress at the micro-interface slip of the composite ceramics, the theoretical expression of the micro-interface slippage stress in the composite ceramic is obtained. And the calculated values are a little higher than the tested values. Quantitative calculations show that if the composite ceramics with triangular symmetrical eutectic groups as the main content produce larger local deformations through the micro-interface slip. The fiber inclusions in the eutectic clusters should have smaller size and larger volume, the micro-interface is the most likely to produce slip.