Effect of defect distribution on thermal expansion coefficient of eutectic composite ceramics

1. Introduction

Thermal expansion problems of composite ceramic materials widely exist in aerospace, military equipment, medical applications and other fields. Regulating the thermal expansion properties of composite ceramic materials is helpful for the preparation of precision parts with controllable thermal expansion, which is of great value for improving equipment sensitivity and optimizing performance. Due to the extremely low temperature during the preparation process, the two phases in the eutectic will be mismatched due to thermal expansion, which inevitably produces thermal mismatched strain. Therefore, the thermal residual stress of composite ceramic material has important theoretical significance and engineering application value. In order to predict the residual thermal stress, it is necessary to have a clear understanding of the effective thermal expansion coefficient of composite ceramic materials.

In recent years, many scholars have done a lot of research on the prediction of thermal expansion coefficient by using different theories and methods. And good results have been obtained for the prediction of thermal expansion properties of composites with similar thin structures. For example, Wu [1] used Eshelby’s equivalent inclusion theory to predict thermal expansion coefficient of inclusion composite with different shapes. Kumar [2] studied the effective thermal expansion coefficient of ceramic particle metal matrix composites by using Eshelby-Mori-Tanaka method. Upadhyay [3] et al. further studied the effective thermal expansion coefficient of granular composites with debonding interfaces by using the three-phase model method. Mohammad [4] and Trofimov [5] predicted the macroscopic thermal expansion coefficient of fiber-reinforced composites with randomly distributed micro-cracks. Hirata [6] deduced the equivalent thermal expansion coefficient of the inclusion interaction, which all obtained good prediction results within a certain range of inclusion content. In addition, the influence of fiber microstructure on thermal expansion coefficient of fiber reinforced composites was calculated by using numerical methods by Li [7] and Liu [8], Sihn [9] using the improved formula of universal single cell model with unknown stress. The thermal expansion coefficient is studied considering the effect of defects. When the defects exceed a certain range and some theoretical results exceed the limit of the thermal expansion coefficient of components, the thermal expansion coefficient model of composite materials with anisotropic matrix needs further improvement.

In the above methods, inclusions are placed in isotropic material to study, but there are few studies on anisotropic matrix materials. In the mesoscale, the effective matrix of composite ceramics is anisotropic, so the model is not universal. The coefficient of thermal expansion is studied considering the effect of defects. When the defects exceed a certain range and some theoretical results exceed the limit of the thermal expansion coefficient of components, the thermal expansion coefficient model of composite materials with anisotropic matrix needs further improvement.

In this paper, four phase model method and interaction direct inference estimation are adopted, and based on Eshelby’s equivalent inclusion theory. According to the different distribution of defects in composites, a universal model of thermal expansion coefficient of eutectic composites was proposed, and the effects of defects and fiber content on thermal expansion coefficient of composites were analyzed.

2. Interaction direct inference estimation in four phase model

It is assumed that ellipsoid inclusions will be randomly distributed in the matrix in the composite. The defects can be considered as special ellipsoidal inclusions with stiffness 0. A representative of the composite ceramic materials selected unit is analyzed, taking containing interface phase inclusions called two phase cell yuan, will be embedded in a two phase cell yuan limited atmosphere constitute three phase cell yuan, substrate material and then to embed the three-phase cell yuan and composite material effective medium constitute four phase model, four phase cell structure model is shown in Fig. 1.

Fig. 1Cell model with defects

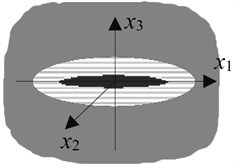
In the model, the inclusions are assumed to be ellipsoid, and $a_1$, $a_2$ and $a_3$ are defined as three main half-axis lengths respectively, where axis $a_1$ is the axis of symmetry of the material. The interface layer and matrix shell around the inclusion have the same shape with the inclusion. The local coordinate system as shown in Fig. 1 is established, and the ellipsoid inclusion can be expressed by the following equation:

In the equation, when $a_1\ll a_2$, $a_3$ represents sheet inclusion, when $a_1\gg a_2$, $a_3$ represents rod or fibrous inclusion. The flexibility increment of the desired effective medium is defined as $\mathbf{H}$. According to the direct estimation method of interaction [10], the following results can be obtained:

where:

where, ${\mathbf{H}}_i$ is the compliance fluctuation of type $I$ inclusions relative to matrix:

${\mathrm{\Omega }}_i$ is the eigen stiffness of inclusion, ${\mathrm{\Omega }}_i={\mathbf{C}}_0(\mathbf{I}-{\mathbf{M}}_i)$, when the composite contains only type $i$ inclusions, the sparse solution as follows:

The equivalent stiffness of eutectic composite ceramics is as follows:

In fibrous inclusions, the components of Eshelby tensor ${\mathbf{M}}_i$ are as follows: $M_{2233}=M_{3322}=\frac{4{\vartheta }_0-1}{8\left(1-{\vartheta }_0\right)}$, $M_{2323}=M_{1313}=\frac{1}{4}$, $M_{1212}=\frac{3-4{\vartheta }_0}{8\left(1-{\vartheta }_0\right)}$, $M_{2222}=M_{3333}=\frac{5-4{\vartheta }_0}{8\left(1-{\vartheta }_0\right)}$, $M_{2211}=M_{3311}=\frac{{\vartheta }_0}{2\left(1-{\vartheta }_0\right)}$. The rest of the components are 0. Where, subscript $i$ represents type $i$ inclusions, subscript 0 represents the matrix, $\mathbf{I}$ represents the fourth-order unit tensor, ${\mathbf{S}}_i$ is the equivalent compliance matrix of type $i$ inclusions, ${\mathbf{S}}_0={\mathbf{C}}_0^{-1}$ represents the compliance matrix of composite ceramic matrix, ${\mathbf{M}}_i$ represents the fourth-order Eshelby tensor corresponding to type $i$ inclusions, $f_i$ represents the volume content of type $i$ inclusions, and ${\vartheta }_0$ represents the Poisson’s ratio of matrix.

3. Equivalent thermal expansion coefficient of eutectic composite ceramics

For ease of calculation, ${\mathbf{\alpha }}_0$ and ${\mathbf{\alpha }}_i$ are used to represent the thermal expansion coefficient matrix of the matrix and the type $i$ inclusions. And the thermal expansion coefficient matrix can be written as follows:

In the above formula, ${\mathbf{\alpha }}^0$ and ${\mathbf{\alpha }}^i$ are used to represent the thermal expansion coefficient. The thermal expansion coefficient matrix of the effective medium representing the composite is indicated by $\mathbf{\alpha }$:

In the above formula, ${\alpha }_{11}$, ${\alpha }_{22}$and ${\alpha }_{33}$ are linear expansion coefficients of composite material along axis 1, 2 and 3 directions. When the temperature of the composite material changes $∆T$, the effective medium thermal strain increment caused by the mismatch of thermal expansion coefficients of each phase in the material is $\epsilon$:

The thermal mismatch strain ${\epsilon }_i$ generated in the inclusion is shown as follows:

According to Eshelby’s theory, the average strain tensor of composite ceramics is as follows:

where, ${\mathrm{\Omega }}_i$ is the intrinsic stiffness tensor of inclusion. ${\mathrm{\Omega }}_i={\mathbf{C}}_i(\mathbf{I}-{\mathbf{M}}_i)$, ${\mathbf{M}}_i$ is the Eshelby tensor corresponding to the inclusion shape, ${\mathbf{C}}_i$ is the stiffness tensor of the inclusion, and ${\mathbf{\sigma }}_i$ is the average stress in the inclusion.

According to the definition of effective thermal expansion coefficient matrix, the average strain tensor of composite ceramic material is as follows:

Then, it can be calculated from Eqs. (9), (11) and (12):

According to Eshelby’s theory, when the thermal strain increment $\epsilon$ is generated, the stress tensor of the matrix is as follows:

where, ${\mathrm{\Omega }}_0$ is the equivalent intrinsic stiffness tensor of the matrix. Equivalent stress tensor in inclusion is as follows:

In the above formula, the $-{\mathrm{\Omega }}_i{\left(\mathbf{I}+{\mathrm{\Omega }}_i{\mathbf{H}}_i\right)}^{-1}{\epsilon }_i$ is the stress tensor caused by the thermal mismatch strain ${\epsilon }_i$ generated in the inclusion, and the ${\left(\mathbf{I}+{\mathrm{\Omega }}_i{\mathbf{H}}_i\right)}^{-1}{\sigma }_0$ is the stress tensor in the inclusion caused by the external load stress tensor. The eigen stiffness tensor of matrix, interface and reinforced fiber are equal because the matrix, interface and reinforced fiber have the same shape and orientation in the fiber reinforced eutectic composite ceramics. Substituting Eqs. (14) and (15) into Eq. (13), the results are as follows:

Here, ${\omega }_i={\left(\mathbf{I}+{\mathrm{\Omega }}_i{\mathbf{H}}_i\right)}^{-1}$, then Eq. (16) can be written as:

According to the defect cell model, axis 1 is the longitudinal direction of the inclusion, and axis 2 and 3 constitute the transverse plane of the inclusion. Then the equivalent thermal expansion coefficient of the composite material can be expressed as follows:

where:

The above compliance increment $H_{1111}$, $H_{1122}$, $H_{2211}$, $H_{2222}$, $H_{2233}$ and the components of Eshelby tensor are given in reference [11].

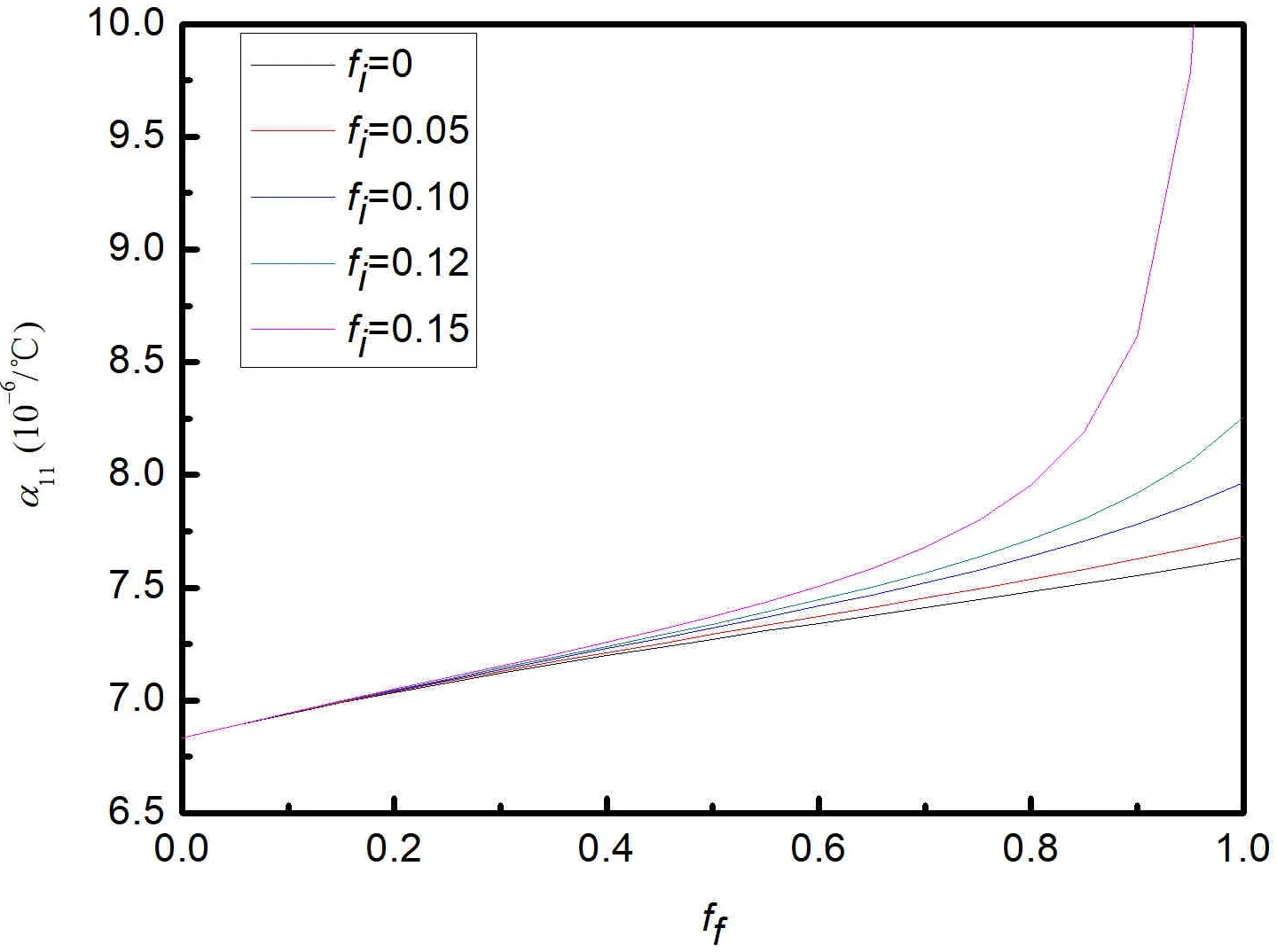
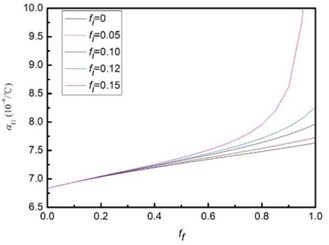
The defects and fibers are regarded as two different types of inclusions distributed in the same matrix. It can be considered that the defects distributed in the matrix form an equivalent matrix, and the fibers distributed in the equivalent matrix. Taking the axis 1 direction as an example, the volume fraction of defective inclusion was $f_i$ and the fiber volume fraction was $f_f$, and the interface phase between defective inclusion and rod-like eutectic was regarded as the general interface to analyze the change of thermal expansion coefficient of composite material at this time, as shown in Fig. 2.

As shown in Fig. 2, the thermal expansion coefficient increases with the increase of fiber content. When the defect content in the matrix is small, the change of thermal expansion coefficient is small. And with the increase of the defect content in the matrix, the thermal expansion coefficient increases significantly. According to the prediction model analysis, if the material matrix is uniform, the thermal expansion coefficient of the material will not change when only the defects are uniformly distributed in the matrix. When the defects and fibers are regarded as two types of inclusion in the matrix at the same time, the prediction result of the effective thermal expansion coefficient of composite material exceeds the range of the thermal expansion coefficient of the matrix or inclusion itself. When there are multiple inclusions in the composite ceramic matrix, the influence of inclusions can always be amplified by defects.

Fig. 2Thermal expansion coefficient of eutectic composite ceramics with different fiber and defect contents

4. Conclusions

A mesoscopic model of eutectic composite ceramics with defects was established according to the mesostructural characteristics of composites. The effective thermal expansion coefficient of eutectic composite containing defects was calculated. And then the influence of defects and inclusions on the effective thermal expansion coefficient is discussed in detail. The results show that the influence of inclusions will be amplified by defects when there are multiple inclusions in the matrix. Therefore, the interaction direct derivative estimate cannot accurately predict the influence of defect distribution on thermal expansion coefficient of eutectic composite ceramics.