Static analysis of dynamic servo tool rest considering the influence of precision error

2.1. Analysis of the gear’s initial error

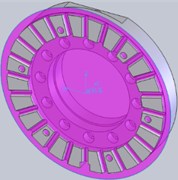
For error analysis (Fig. 1), the plane formed by the median line of the dynamic servo tool rest’s ideal tooth disc surface is defined as the node plane. Tool rest and gear disc coordinate systems are also defined. The symmetrical centre relative to each tooth in the plane of tooth disc are determined, and this point is taken as the origin of the tool rest coordinate system.

Fig. 1Pitch plane of gear plate

2.2. Analysis of angular error

To facilitate differentiation and identification, the subscript $n$ is taken as the serial number of each shaft, $m$ as the two ends of the shaft, and $i$ as the serial number of each gear pair.

The angular error is distributed in the periphery of the gear disc and follows normal distribution. Error of assembly and machining of the gear mainly cause angular errors [8-10].

The angular error caused by gear machining error is:

where $F_{inm}^{\text{'}}$ is the total deviation of tangential synthesis, $d_{nm}$ is gear dividing circle diameter, and ${\delta }_{nm1}$ is the gear angular error.

The normal distribution function is used to analyse the working error. Therefore:

where $u\left({\delta }_{nm1}\right)$ is the standard uncertainty for the angular motion of gears.

The assembly error will cause the gear to jump in the process of rotation, thereby causing the angular error of shafting:

where $u\left(e_n\right)$ is the standard uncertainty for radial errors, ${\alpha }_{nm}$ is the pressure angle, and $u\left({\delta }_{nm2}\right)$ is the standard uncertainty of angular error.

The sensitive error direction refers to the radial direction of the bearing because the inner and outer rings of the bearing are equivalent to thin-walled parts. As such:

where $u\left(e_{n0}\right)$ is the standard uncertainty of coaxiality of axial diameter, $u\left(e_{nm1}\right)$ is the roundness deviation degree of the axis, $u\left(e_{nm2}\right)$ is the deviation degree of the bearing relative to its ideal axis, and $u\left(E_{nm1}\right)$ is the standard uncertainty:

where $e_{n0}$ is the coaxiality of axial diameters at both ends:

where $e_{nm1}$ is the difference between the journal and the ideal roundness, and $e_{nm2}$ is the relative difference of axis.

The error caused by eccentric connection between gear and shaft is:

where $e_{nm}$ is the gear eccentricity, and $u\left({\delta }_{nm3}\right)$ is the standard uncertainty of angular motion caused by the eccentric connection between the gear and the shaft.

The angular error of transmission mechanism is:

where $u\left({\delta }_{nm}\right)$ is the synthetic standard uncertainty of angular motion of a single gear:

where $i_{nm}$ is the transmission ratio, and $u\left(\delta \right)$ is the synthetic standard uncertainty of the angular motion of the transmission mechanism.

3.1. Initial position error of tooth disc

The radial, axial, inclination and phase error angles of fixed and locking tooth discs can be determined by decomposing the initial position error of the tooth disc (Table 1).

3.2. Tooth disc machining error

The inaccurate milling of a cutter in the axial position results in tooth thickness error. Particularly, when the direction of the linear movement of the milling cutter does not coincide with the coordinate system of the tooth disc, the error will be generated. Inaccurately relative inclination of milling cutter will generate tooth shape half angle error (Fig. 2).

Fig. 2Gear plate machining error

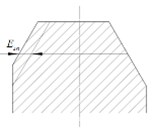
a) Tooth thickness error

b) Tooth error

c) Toothed half-angle error

(a) Tooth thickness tolerance:

where $F_{er}$ is the equivalent axial run-out tolerance, $b_{er}$ is the equivalent tooth radial feed tolerance, ${\alpha }_e$ is the tooth profile angle, and $u\left(T_{sn}\right)$ is the standard uncertainty of tooth thickness tolerance.

(b) Tooth alignment error:

where $e\beta$ is equivalent helicaland $L_{e\beta }$ is the measuring range of equivalent helical, ${\alpha }_e$ is the tooth profile angle, where $eH\beta$ is the equivalent helical deviation and $f_{eH\beta }$ is the equivalent helical inclination deviation, and $u\left(\varphi \right)$ is the standard uncertainty of tooth direction error.

(c) Half-angle error of tooth profile:

where $eH\alpha$ is the equivalent tooth profile and $L_{e\alpha }$ is the range of equivalent tooth profile, where $eH\alpha$ is the equivalent profile deviation and, $f_{eH\alpha }$ is the equivalent profile inclination deviation, and $u\left(∆\frac{\alpha }{2}\right)$ is the standard uncertainty of half-angle error of tooth profile.

The tooth thickness, tooth direction and half-angle errors of tooth shape can be determined by using Eqs. (10-12), respectively (Table 2).

4.1. Static analysis of error-free gear disc

The moving tooth disc and the main shaft are simplified into fixed rigid connections without the role of bolt holes. The errorless tooth disc mesh is hexahedral element. The tooth surface of the locking tooth disc is set as the target surface, and the two other tooth surfaces are the contact surface ‚according to the position connection relation of the three tooth discs. The target element is targe 170, and the contact element is contat 173. A full restraint is applied on the outer circle far from the moving and fixed tooth discs. Then, a uniform pressure load is applied at the connection point between the locking tooth disc and the piston. Equivalent displacement and Equivalent stress diagram are shown in Fig. 3.

Fig. 3Equivalent displacement and Equivalent stress diagram

a)Displacement of dynamic tooth disc

b) Displacement of lock tooth disc

c) Displacement of fixed tooth disc

d) Stress of dynamic tooth disc

e) Stress of lock tooth disc

f) Stress of fixed tooth disc

4.2. Statics analysis of toothed disc with error

The machining and positioning errors of the tooth disc will affect working performance. When the contact pair is established, the effect is taken into account, and the influence of the positioning error of the tooth disc of the tool holder is introduced to establish the contact pair with the error, and then the solution is carried out, which are shown in Fig. 4.

Fig. 4Equivalent displacement and Equivalent stress diagram

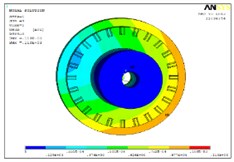
a)Displacement of dynamic tooth disc

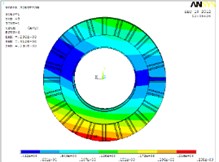
b) Displacement of lock tooth disc

c) Displacement of fixed tooth disc

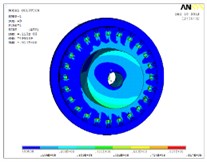
d) Stress of dynamic tooth disc

e) Stress of lock tooth disc

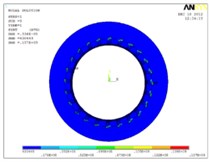
f) Stress of fixed tooth disc

The force on the tooth disc with error is uneven, and the maximum error of the extreme stress distribution can reach 142.28 % based on the static analysis results of the errorless gear in Table 3. Meanwhile, local deformation is also relatively large, and the maximum error of deformation extremum can reach 1371.35 %. Thus, the initial error of tool rest will impact the positioning accuracy of the tooth disc greatly.