Construction of 12 DOFs spur gear coupling dynamic model

Lv, Huanchao; Li, Zhengminqing; Zhu, Wenlin; Tang, Xin; Gao, Jie; Zhu, Rupeng

doi:10.21595/vp.2019.21028

Vibroengineering Procedia

Browse Procedia

Published: 19 October 2019

Check for updates

Construction of 12 DOFs spur gear coupling dynamic model

Huanchao Lv¹

Zhengminqing Li²

Wenlin Zhu³

Xin Tang⁴

Jie Gao⁵

Rupeng Zhu⁶

^{1, 2, 6}National Key Laboratory of Science and Technology on Helicopter Transmission, Nanjing University of Aeronautics and Astronautics, Nanjing, 210016, China

^{3, 4, 5}Science and Technology on Helicopter Transmission Laboratory, AECC Hunan Aviation Powerplant Research Institute, Zhuzhou, 412002, China

Corresponding Author:

Zhengminqing Li

Cite the article Download PDF

Downloads 1317

CrossRef Citations 2

Abstract

A 12-degree-of-freedom (DOF) spur gear dynamic model is constructed, which is coupled by the mesh gear pair and the gearbox. The construction method of spur gear coupling dynamic model, based on lumped mass method, is better than finite element method, due to higher modeling efficiency. The work would be benefit to spur gear coupling dynamic modeling and analyses.

Highlights

A dynamic model coupled by the mesh gear pair and the gearbox is constructed.
The construction method of spur gear coupling dynamic model is more efficient.
Using modal assurance criterion to verify the accuracy of the proposed method.

1. Introduction

Gear dynamic models are focused by many scholars. There is an extensive body of literatures on it [1-9]. Jin et al. established gear dynamic models coupled with bending-torsion-axis-swing of mesh pairs based on lumped mass method [10]. Zhu et al. constructed finite element models of the gear transmission, and evaluated dynamic behavior of the system [11, 12]. Ren et al. proposed a construction method of gear dynamic models based on substructure method [13-15]. However, the gear coupling dynamic models associated with mesh pairs and gearbox supports are few studied. Thus, in the paper, a 12 DOFs spur gear coupling dynamic model, based on lumped mass method, is proposed. The work would be helpful to the spur gear coupling dynamic analyses.

2. Construction of 12DOFs dynamic model

The gear transmission system is mainly composed of two spur gears, bearings and gearbox supports. When modeling with the finite element method, it is inefficient because of the complexity of the gearbox supports. Therefore, a 12 DOFs coupling dynamic model based on lumped mass method is established, as shown in Fig. 1.

Fig. 1The coupling dynamic model

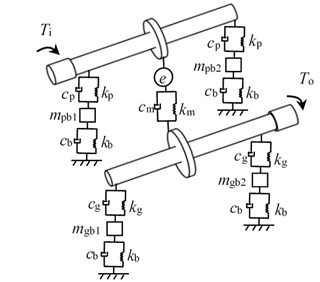
As illustrated in Fig. 1, subscript $p$ and $g$ express driving gear and driven gear, respectively, $k$ is a bending stiffness, $c$ is a bending damping, $k_{m}$ is a mesh stiffness, $c_{m}$ is a mesh damping, $e$ is a static transmission errors (STE), $T_{i}$ is the input torsion, $T_{o}$ is the output torsion, $k_{b}$ is the support stiffness, $c_{b}$ is the support damping. Moreover, $m_{p b 1}$ , $m_{p b 2}$ , $m_{g b 1}$ and $m_{g b 2}$ are the equivalent masses of the gearbox supports.

As given in Fig. 1, the mathematical equations of the meshing pair could be derived by:

1

\{\begin{array}{l} m_{p} {\ddot{l}}_{p} + c_{p} {\dot{l}}_{p} + k_{p} l_{p} - F_{m} = 0, \\ m_{g} {\ddot{l}}_{g} + c_{g} {\dot{l}}_{g} + k_{g} l_{g} + F_{m} = 0, \\ I_{i} {\ddot{θ}}_{i} + c_{1} ({\dot{θ}}_{i} - {\dot{θ}}_{p}) + k_{1} (θ_{i} - θ_{p}) = T_{i}, \\ I_{p} {\dot{\ddot{θ}}}_{p} - c_{1} ({\dot{θ}}_{i} - {\dot{θ}}_{p}) - k_{1} (θ_{i} - θ_{p}) - r_{p} \cdot F_{m} = 0, \\ I_{g} {\ddot{θ}}_{g} + c_{2} ({\dot{θ}}_{g} - {\dot{θ}}_{o}) + k_{2} (θ_{g} - θ_{o}) + r_{g} \cdot F_{m} = 0, \\ I_{o} {\ddot{θ}}_{o} - c_{2} ({\dot{θ}}_{g} - {\dot{θ}}_{o}) - k_{2} (θ_{g} - θ_{o}) = - T_{o}, \end{array}

where subscript $i$ and $o$ express motor and load, respectively, $θ$ is a torsion degree, $l$ is a bending degree, $m$ is a mass, $r$ is a base circle radius, $I$ is a moment of inertia, $k_{1}$ and $k_{2}$ are torsional stiffness of the shaft, $c_{1}$ and $c_{2}$ are torsional damping of the shaft, and $F_{m}$ could be deduced as:

2

F_{m} = k_{m} \cdot (r_{g} θ_{g} - r_{p} θ_{p} + e + l_{g} - l_{p}) + c_{m} \cdot (r_{g} {\dot{θ}}_{g} - r_{p} {\dot{θ}}_{p} + \dot{e} + {\dot{l}}_{g} - {\dot{l}}_{p}) .

The gearbox supports dynamic equivalent model is proposed, as shown in Fig. 2.

Fig. 2The gearbox supports dynamic equivalent model

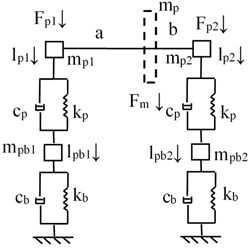
a) Equivalent model of the driving gear

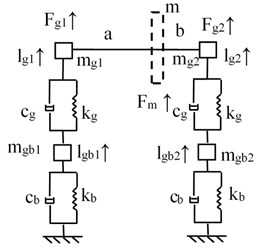
b) Equivalent model of the driven gear

As illustrated in Fig. 2, the equivalent mass of the gears at the bearing fulcrum could be deduced as:

3

\{\begin{array}{l} m_{p 1} = m_{p} \cdot \frac{b}{a + b}, \\ m_{p 2} = m_{p} \cdot \frac{a}{a + b}, \\ m_{g 1} = m_{g} \cdot \frac{b}{a + b}, \\ m_{g 2} = m_{g} \cdot \frac{a}{a + b}, \end{array}

where $a$ and $b$ are the distance from the gear to the bearing fulcrum.

As given in Fig. 2, the mathematical equations of the support structure could be derived by:

4

\{\begin{array}{l} m_{p 1} {\ddot{l}}_{p 1} + c_{p} ({\dot{l}}_{p 1} - {\dot{l}}_{p b 1}) + k_{p} (l_{p 1} - l_{p b 1}) - F_{p 1} = 0, \\ m_{p b 1} {\ddot{l}}_{p b 1} + c_{b} {\dot{l}}_{p b 1} + k_{b} l_{p b 1} - c_{p} ({\dot{l}}_{p 1} - {\dot{l}}_{p b 1}) - k_{p} (l_{p 1} - l_{p b 1}) = 0, \\ m_{g 1} {\ddot{l}}_{g 1} + c_{g} ({\dot{l}}_{g 1} - {\dot{l}}_{g b 1}) + k_{g} (l_{g 1} - l_{g b 1}) - F_{g 1} = 0, \\ m_{g b 1} {\ddot{l}}_{g b 1} + c_{b} {\dot{l}}_{g b 1} + k_{b} l_{g b 1} - c_{g} ({\dot{l}}_{g 1} - {\dot{l}}_{g b 1}) - k_{g} (l_{g 1} - l_{g b 1}) = 0, \\ m_{p 2} {\ddot{l}}_{p 2} + c_{p} ({\dot{l}}_{p 2} - {\dot{l}}_{p b 2}) + k_{p} (l_{p 2} - l_{p b 2}) - F_{p 2} = 0, \\ m_{p b 2} {\ddot{l}}_{p b 2} + c_{b} {\dot{l}}_{p b 2} + k_{b} l_{p b 2} - c_{p} ({\dot{l}}_{p 2} - {\dot{l}}_{p b 2}) - k_{p} (l_{p 2} - l_{p b 2}) = 0, \\ m_{g 2} {\ddot{l}}_{g 2} + c_{g} ({\dot{l}}_{g 2} - {\dot{l}}_{g b 2}) + k_{g} (l_{g 2} - l_{g b 2}) - F_{g 2} = 0, \\ m_{g b 2} {\ddot{l}}_{g b 2} + c_{b} {\dot{l}}_{g b 2} + k_{b} l_{g b 2} - c_{g} ({\dot{l}}_{g 2} - {\dot{l}}_{g b 2}) - k_{g} (l_{g 2} - l_{g b 2}) = 0 . \end{array}

According to the deformation coordination relationship, as shown in Fig. 3, the deformation coordination equations could be derived by:

5

\{\begin{array}{l} l_{p} = \frac{b l_{p 1} + a l_{p 2}}{a + b}, \\ l_{g} = \frac{b l_{g 1} + a l_{g 2}}{a + b} . \end{array}

Fig. 3The coordination relationship

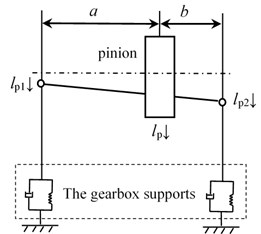
According to the deformation coordination Eq. (5), Eq. (1) and Eq. (4), a 12 DOFs coupling dynamic model, based on lumped mass method, is established.

3. Simulations

In order to verify the accuracy of the proposed method, the parameters of an example case are listed in Table 1.

Table 1Parameters of system

Symbol name	Value	Unit
Modulus / $m$	4	mm
Pressure angle / $α$	20	°
Tooth number of driving gear / $z_{1}$	23	–
Tooth number of driven gear / $z_{2}$	69	–
Addendum coefficient / $h_{a}^{*}$	1	–
Clearance coefficient / $c^{*}$	0.25	–

According to the 12 DOFs coupling dynamic model and the parameters listed in Table 1, the natural frequencies of the example case are simulated. Part of the results are shown in Fig. 4.

In the case of Fig. 4, the natural vibration mode vector of the first-order non-zero natural frequency (second frequency: 1403 Hz) is:

6

\begin{array}{l} ϕ_{A} = \{0.3211, - 0.0149,0.0050, - 0.9469, - 0.0004, - 0.0002, \\ - 0.0004, - 0.0002, - 0.0004, - 0.0002, - 0.0004, - 0.0002\} \end{array}

Fig. 4Natural frequency simulations

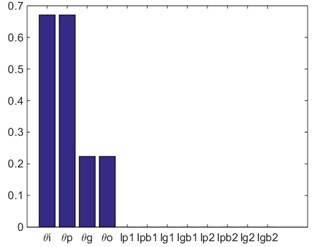
a) First frequency: 0 Hz

b) Second frequency: 1403 Hz

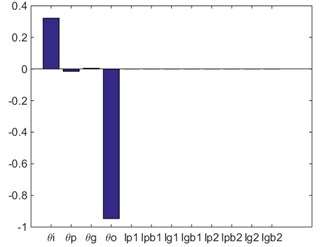
According to the simulation result based on finite element model, as shown in Fig. 5, the natural vibration mode vector could be expressed as:

7

ϕ_{B} = \{- 0.2524, 0, 0, 0.7573, 0, 0, 0, 0, 0, 0, 0, 0\} .

Fig. 5Natural vibration mode based on FEM (natural frequency: 1282.9 Hz)

According to the modal assurance criterion (MAC), Eq. (6) and Eq. (7), the natural vibration mode vector correlation can be derived by:

8

M A C = \frac{{|ϕ_{B}^{T} ϕ_{A}|}^{2}}{ϕ_{B}^{T} ϕ_{B} ϕ_{A}^{T} ϕ_{A}} .

According to Eq. (8), the MAC value of the example case is 0.9997, namely, the natural vibration mode shown in Fig. 4(b) and the natural vibration mode shown in Fig. 5 are the same-order physical mode. The relative error of the natural frequencies between two methods is calculated, as shown in Table 2.

Table 2The relative error of the natural frequencies between two methods

	Value	Unit
The natural frequency based on lumped mass method	1403	Hz
The natural frequency based on FEM	1282.9	Hz
The relative error	9.36	%

In the case of Table 2, the relative error of the natural frequencies between two methods is 9.36 %, namely, the proposed method is accurate and feasible.

4. Conclusions

In the issue, a 12 DOFs spur gear coupling dynamic model, based on lumped mass method, is proposed. The construction method of spur gear coupling dynamic model is better than finite element method, because it enables rapid modeling of complex gearbox and makes dynamic modeling more efficient. This contribution would be helpful to the spur gear coupling dynamic modeling and analyses.

References

Mark W. D. Use of the generalized transmission error in the equations of motion of gear systems. Journal of Mechanical Design, Vol. 109, Issue 2, 1987, p. 283-291.

Publisher
Şener Ö. S., Özgüven H. N. Dynamic analysis of geared shaft systems by using a continuous system model. Journal of Sound and Vibration, Vol. 166, Issue 3, 1993, p. 539-556.

Publisher
Walha L., Louati J., Fakhfakh T., et al. Dynamic Response of Two-Stage Gear System Damaged by Teeth Defects. Oficyna Wydawnicza Politechniki Warszawskiej, 2005.

Search CrossRef
Bodas A., Kahraman A. Guda-1 influence of carrier and gear manufacturing errors on the static planet load sharing behavior of planetary gear sets (gear unit design and applications). The Japan Society of Mechanical Engineers, 2017, p. 633-638.

Publisher
Li Z., Zhu R. Sensitivity predictions of geometric parameters on engagement impacts of face gear drives. Journal of Vibroengineering, Vol. 17, Issue 5, 2015, p. 2236-2246.

Search CrossRef
Hu Z. H., Tang J. Y., Chen S. Y., Lei D. C. Effect of mesh stiffness on the dynamic response of face gear transmission system. Journal of Mechanical Design, Vol. 135, Issue 7, 2013, p. 071005.

Publisher
Fernandez A., Garcia P., Ibarbia A. D. Enhanced model of gear transmission dynamics for condition monitoring applications: Effects of torque, friction and bearing clearance. Mechanical Systems and Signal Processing, Vol. 85, 2017, p. 445-467.

Publisher
Rigaud E., Sabot Effect J. Elasticity of shafts, bearings, casing and couplings on the critical rotational speeds of a gearbox. Physics, Vol. 1230, 2007, p. 833-845.

Search CrossRef
Shaobin L. Study on Coupled Thermo-Elastic Deformation and Nonlinear Dynamic Emulate about High-Speed, Heavy-Load Gear Transmission System. Chongqing University, 2004.

Search CrossRef
Jin G., Zhu R., Bao H. Nonlinear dynamical characteristics of face gear transmission system. Journal of Central South University, Vol. 5, Issue 41, 2010, p. 1807-1813.

Search CrossRef
Zhu C. C., Lu B., Xu X. Y., et al. Analysis of coupling characteristics of transmission system and structural system of high power marine gearbox. Journal of Ship Mechanics, Vol. 15, Issue 11, 2011, p. 1315-1321.

Search CrossRef
Zhu C. C., Lu B., Xu X. Y., et al. Analysis of heavy duty marine gearbox with thermal-elastic coupling. Journal of Ship Mechanics, Vol. 15, Issue 8, 2011, p. 898-905.

Search CrossRef
Ren Y. F., Chang S., Liu G., et al. Analysis of influence of box flexibility on dynamic characteristics of gear transmission system. Journal of Vibration and Shock, Vol. 14, 2017.

Publisher
Liu L., Zhao C. Q., Ren Y. F., et al. Dynamic modeling and box influence analysis of gearbox fully coupled system. Journal of Harbin Engineering University, Vol. 39, Issue 3, 2018, p. 561-568.

Search CrossRef
He Z. X., Zhao C. Q., Ren Y. F., et al. Dynamic response analysis of planetary gear transmission system with coupling box vibration. Journal of South China University of Technology, Vol. 9, 2015, p. 128-134.

Search CrossRef

Cited by

Meshing Mechanism and Simulation Analysis of Silent Chain Based on Rigid-Flexible Intelligent Dynamics Technology

Song Ding | Jun Ye

(2022)

A Generalized Dynamic Model and Coupling Meshing Force Analysis for Planetary Gear Set Transmissions

Haiwei Wang | Cheng Ji | Fengxia Lu | Cheng Wang | Xueyan Sun

(2022)

About this article

Received

17 September 2019

Accepted

01 October 2019

Published

19 October 2019

SUBJECTS

System dynamics in manufacturing system modeling

DOI

https://doi.org/10.21595/vp.2019.21028

Keywords

spur gear

coupling dynamic model

12 DOFs

Acknowledgements

The authors are grateful for the financial support provided by the National Natural Science Foundation of China under No. 51775264, and by National Key Laboratory of Science and Technology on Helicopter Transmission (Nanjing University of Aeronautics and Astronautics) (Grant No. HTL-A-19G06). In addition, the authors declare that there is no conflict of interests regarding the publication of this article.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 12 30

Modelling and dynamic behaviours of a high-contact-ratio spur-gear system considering rough surface

Zhenbang Cheng, Yu Zhou, Zhengyu Liu

Research article

2023 09 14

Experimental study and comparative analysis of pitting fault in spur gear system

Kemajou Herbert Yakeu Happi, Bernard Xavier Tchomeni Kouejou, Alfayo Anyika Alugongo

Research article

2020 02 15

Dynamic simulation analysis of spur gear space driven system with large inertia load

Chao Li, Jianfeng Ma, Xuehao Yin, Hongbin Yang

Research article

2017 02 15

A dynamic modeling method for helical gear systems

Ming Yan, Hong-quan Liu

H. Lv, Z. Li, W. Zhu, X. Tang, J. Gao, and R. Zhu, “Construction of 12 DOFs spur gear coupling dynamic model,” Vibroengineering PROCEDIA, Vol. 28, pp. 241–245, Oct. 2019, https://doi.org/10.21595/vp.2019.21028

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2019.21028
UR  - https://doi.org/10.21595/vp.2019.21028
TI  - Construction of 12 DOFs spur gear coupling dynamic model
T2  - Vibroengineering PROCEDIA
AU  - Li, Zhengminqing
AU  - Lv, Huanchao
AU  - Zhu, Wenlin
AU  - Tang, Xin
AU  - Gao, Jie
AU  - Zhu, Rupeng
PY  - 2019
DA  - 2019/10/19
PB  - JVE International Ltd.
SP  - 241-245
VL  - 28
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Li_2019,
	doi = {10.21595/vp.2019.21028},
	url = {https://doi.org/10.21595/vp.2019.21028},
	year = 2019,
	month = {oct},
	publisher = {{JVE} International Ltd.},
	volume = {28},
	pages = {241--245},
	author = {Zhengminqing Li and Huanchao Lv and Wenlin Zhu and Xin Tang and Jie Gao and Rupeng Zhu},
	title = {Construction of 12 {DOFs} spur gear coupling dynamic model},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]Z. Li, H. Lv, W. Zhu, X. Tang, J. Gao, and R. Zhu, “Construction of 12 DOFs spur gear coupling dynamic model,” Vibroengineering PROCEDIA, vol. 28, pp. 241–245, Oct. 2019, doi: 10.21595/vp.2019.21028.

Copy IEEE

Copied to clipboard!

Li, Zhengminqing, Huanchao Lv, Wenlin Zhu, Xin Tang, Jie Gao, and Rupeng Zhu. “Construction of 12 DOFs Spur Gear Coupling Dynamic Model.” Vibroengineering PROCEDIA 28 (October 19, 2019): 241–45. https://doi.org/10.21595/vp.2019.21028.

Copy Chicago

Copied to clipboard!

Construction of 12 DOFs spur gear coupling dynamic model

Abstract

Highlights

1. Introduction

2. Construction of 12DOFs dynamic model

3. Simulations

4. Conclusions

References

Cited by

About this article

Related Articles