A dynamic modeling method for helical gear systems

Dynamic modeling for gear systems is very important for accurately predicting the dynamic responses during the gear engagements. During the modeling, meshing force must be determined, and it is usually calculated by the product of the relative displacement along the line of action (LOA) and the meshing stiffness. At present, the relative displacement calculation for helical gear systems is very complicated by several existing methods because the complicated geometric relationships need to be derived for determining the spatial positions of two meshing points along LOA. In this study, a simple method for calculating the relative displacement along LOA is presented based on ANSYS software. And on this basis, a new finite element modeling method for a helical gear transmission system with multiple shafts is developed, where the influences of shafts and bearing flexibilities are considered. Moreover, the proposed method is validated by comparing the dynamic characteristics, such as natural characteristics and vibration responses, with those obtained from Kubur’s method and Zhang’s method.

1. Introduction

Dynamic characteristics of geared systems are closely related to the noise and reliability of the system. The dynamic loads during the gear transmission can lead to larger dynamic stress which may threaten the security operation of the gear systems [1-3]. Therefore, a good dynamic modeling method for gear systems is essential for accurately predicting the vibration responses during gear engagement. Moreover, such a model can also be used to the dynamic design for the gear pairs, shafts and bearings.

A lot of researches on the dynamic characteristics of the spur gear rotor systems were carried out, such as Iida et al. [4], Choy et al. [4], Kahraman and Singh [6], Lim and Singh [7], Özgüven [8], Kahraman et al. [9], Rao et al. [10], Jia et al. [11], Lee et al. [12] and Ma et al. [13-17]. Except for the dynamics of spur gear systems, many researchers also developed many mathematical models for simulating the dynamic characteristics of spur gear systems. Blankenship and Singh [18] developed a new mesh dynamic model for gear pairs, which can provide a true, three-dimensional representation of the forces and moments during the gear engagement. Velex and Maatar [19] presented a general method for simulating 3D gear meshing, and introduced this meshing model into a lumped mass model of a gear system, and analyzed some parameters such as meshing stiffness and installation error on the system vibration responses. Choi et al. [20] studied the coupled lateral, torsional and axial vibrations of a gear system using finite element method. In their model, the tooth engagement was modeled using distributed spring and the force vibrations caused by unbalances and static transmission errors were also calculated. Baud and Velex [21] developed a finite element model for simulating dynamic tooth loads in gear rotor systems and verified the model by experiments using a single spur and helical gear reducer which includes flexible shafts mounted hydrostatic bearings. Kubur et al. [1, 2] proposed a new model for simulating the dynamic characteristics of a helical system with multiple shafts. In their model, the shafts are modeled using finite element method and the helical gear pairs are modeled using a lumped mass model. Based on Kubur’s model, Zhang et al. [22] established a general mathematical model of helical gear systems considering the effects of geometric eccentricity, gear meshing, bearing stiffness, and shaft flexibility. Based on the previous works in [1, 2, 22], Zhang et al. [23] developed a finite element model of a rotor system in centrifugal compressor. In their model, the effects of the constant meshing stiffness of helical gear pairs, the varying stiffness and damping of the bearings on the system vibration responses are considered.

From the above literature analysis, it is clear that the dynamic models of gear pairs are very complicated, especially, in the calculation of the relative displacement along the line of action. This study focuses on a new mathematical model for a rotor system with helical gear pairs and multiple shafts by ANSYS software. This new model can easily calculate the relative displacement and meshing force using the geometric positions of the meshing points.

2. Dynamic models of geared rotor systems

In this section, a new modeling method for geared rotor systems is developed in ANSYS software. The proposed model is verified by comparing the vibration behaviors with those obtained from Zhang’s model [22]. A brief introduction to Zhang’s model (see Figs. 1(a) and (b)) is described in Section 2.1, and the proposed model (see Figs. 1(c) and (d)) is introduced in Section 2.2.

Fig. 1a) Schematic of geared rotor systems, b) 3D model of the helical gear pair ij, c) FE model of the gear rotor system, d) projection drawing in y-direction

a) Schematic of geared rotor systems, b) 3D model of the helical gear pair ij, c) FE model of the gear rotor system, d) projection drawing in y-direction

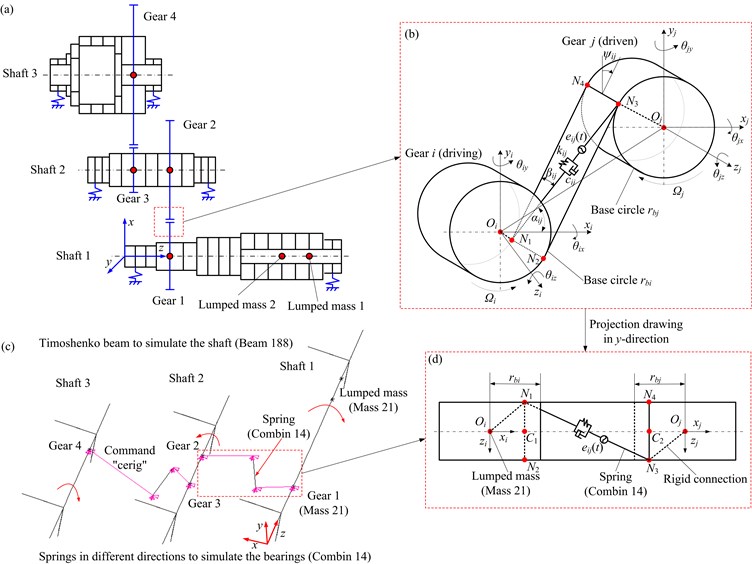
2.1. Dynamic models of geared rotor systems using Zhang’s method

A 3D mathematical model of helical gear pair with 12 degrees of freedom (DOFs) is displayed in Fig. 1(b), which includes two helical gears ( $i$ and $j$ ). $Ω_{i}$ , $Ω_{j}$ , $O_{i}$ , $O_{j}$ , $r_{b i}$ and $r_{b j}$ denote the rotational speeds, geometrical centers, radii of base circles of the gears $i$ and $j$ . The flexible of gears are ignored and assumed to be the rigid disks. In addition, a spring-damping setting is adopted to simulate the gear meshing and the direction is defined according to the helix angle $β_{i j}$ . The spring stiffness is determined by the average gear mesh stiffness due to the high contact ratio of helical gear. It is worth noting that Zhang’s method in Ref. [22] takes the effects of gear geometric eccentricity into account. However, in this paper the eccentric effect is ignored. Helix angle $β_{i j}$ is defined as:

1

β_{i j} = \{\begin{array}{l} > 0, & if gear i has left hand teeth, \\ = 0, & if gear i is a spur gear, \\ < 0, & if gear i has right hand teeth . \end{array}

As shown in Fig. 1(b), the angle between the connecting line of gear centers and the positive $x$ -axis of gear $i$ is defined as relative position angle $α_{i j}$ . The angle between the plane of action and positive $y$ -axis can be defined by $ψ_{i j}$ . Under different direction of rotation of driving gear, $ψ_{i j}$ can be expressed as follows:

2

ψ_{i j} = \{\begin{array}{l} - φ_{i j} + α_{i j}, & Ω_{i} : Couterclockwise, \\ φ_{i j} + α_{i j} - π, & Ω_{i} : Clockwise, \end{array}

where $φ_{i j}$ is the lateral pressure angle of gear pairs.

The meshing position changes under the different direction of rotation of the driving gear. Considering this changing, a sgn function can be defined as follows:

3

s g n = \{\begin{array}{l} 1, & Ω_{i} : Couterclockwise, \\ - 1, & Ω_{i} : Clockwise . \end{array}

The displacement vector of the gear pair $i j$ can be written as follows:

4

X_{i j} = [x_{i}, y_{i}, z_{i}, θ_{x i}, θ_{y i}, θ_{z i}, x_{j}, y_{j}, z_{j}, θ_{x j}, θ_{y j}, θ_{z j}]^{T} .

Due to the equilibriums of lateral motion and force, the equations of motion of the gear pair $i j$ can be written as the following expressions, where the influence of the geometric eccentricity of gear is ignored:

5

\{\begin{array}{l} m_{i} {\ddot{x}}_{i}^{} - k_{i j} p_{i j} (t) c o s β_{i j} s i n ψ_{i j} - c_{i j} {\dot{p}}_{i j} (t) c o s β_{i j} s i n ψ_{i j} = 0, \\ m_{i} {\ddot{y}}_{i}^{} + k_{i j} p_{i j} (t) c o s β_{i j} c o s ψ_{i j} + c_{i j} {\dot{p}}_{i j} (t) c o s β_{i j} c o s ψ_{i j} = 0, \\ m_{i} {\ddot{z}}_{i}^{} + s g n \times k_{i j} p_{i j} (t) s i n β_{i j} + s g n \times c_{i j} {\dot{p}}_{i j} (t) s i n β_{i j} = 0, \\ I_{i x} {\ddot{θ}}_{x i}^{} + k_{i j} p_{i j} (t) s i n β_{i j} r_{b i} s i n ψ_{i j} + c_{i j} {\dot{p}}_{i j} (t) s i n β_{i j} r_{b i} s i n ψ_{i j} + I_{i z} Ω_{i} {\dot{θ}}_{y i}^{} = 0, \\ I_{i y} {\ddot{θ}}_{y i}^{} - k_{i j} p_{i j} (t) s i n β_{i j} r_{b i} c o s ψ_{i j} - c_{i j} {\dot{p}}_{i j} (t) s i n β_{i j} r_{b i} c o s ψ_{i j} - I_{i z} Ω_{i} {\dot{θ}}_{x i}^{} = 0, \\ I_{i z} {\ddot{θ}}_{z i}^{} + s g n \times k_{i j} p_{i j} (t) r_{b i} c o s β_{i j} + s g n \times c_{i j} {\dot{p}}_{i j} (t) r_{b i} c o s β_{i j} = s g n \times T_{i}, \\ m_{j} {\ddot{x}}_{j}^{} + k_{i j} p_{i j} (t) c o s β_{i j} s i n ψ_{i j} + c_{i j} {\dot{p}}_{i j} (t) c o s β_{i j} s i n ψ_{i j} = 0, \\ m_{j} {\ddot{y}}_{j}^{} - k_{i j} p_{i j} (t) c o s β_{i j} c o s ψ_{i j} - c_{i j} {\dot{p}}_{i j} (t) c o s β_{i j} c o s ψ_{i j} = 0, \\ m_{j} {\ddot{z}}_{j}^{} - s g n \times k_{i j} p_{i j} (t) s i n β_{i j} - s g n \times c_{i j} {\dot{p}}_{i j} (t) s i n β_{i j} = 0, \\ I_{j x} {\ddot{θ}}_{x j}^{} + k_{i j} p_{i j} (t) s i n β_{i j} r_{b j} s i n ψ_{i j} + c_{i j} {\dot{p}}_{i j} (t) s i n β_{i j} r_{b j} s i n ψ_{i j} + I_{j z} Ω_{j} {\dot{θ}}_{y j}^{} = 0, \\ I_{j y} {\ddot{θ}}_{y i}^{} - k_{i j} p_{i j} (t) s i n β_{i j} r_{b j} c o s ψ_{i j} - c_{i j} {\dot{p}}_{i j} (t) s i n β_{i j} r_{b j} c o s ψ_{i j} - I_{j z} Ω_{j} {\dot{θ}}_{x j}^{} = 0, \\ I_{j z} {\ddot{θ}}_{z j}^{} + s g n \times k_{i j} p_{i j} (t) r_{b j} c o s β_{i j} + s g n \times c_{i j} {\dot{p}}_{i j} (t) r_{b j} c o s β_{i j} = s g n \times T_{j}, \end{array}

where $m_{i}$ and $m_{j}$ denote the masses of gear $i$ and gear $j$ . $I_{i x}$ , $I_{i y}$ , $I_{i z}$ , $I_{j x}$ , $I_{j y}$ and $I_{j z}$ are the moments of inertia about $x$ , $y$ and $z$ axis. $k_{i j}$ denotes the averaged meshing stiffness of gear pair $i j$ . $c_{i j}$ represents the meshing damping of gear pair $i j$ . In a direction, normal to contact surface, the relative displacement of gear mesh is written as:

6

p_{i j} (t) = [- x_{i} s i n ψ_{i j} + x_{j} s i n ψ_{i j} + y_{i} c o s ψ_{i j} - y_{j} c o s ψ_{i j} + s g n \times r_{b i} θ_{z i} + s g n \times r_{b j} θ_{z j}] c o s β_{i j}

+ [s g n \times z_{i} - s g n \times z_{j} + r_{b i} s i n ψ_{i j} θ_{x i} + r_{b j} s i n ψ_{i j} θ_{x j} - r_{b i} θ_{y i} c o s ψ_{i j} - r_{b j} θ_{y j} c o s ψ_{i j}] s i n β_{i j}

- e_{i j} (t),

where $e_{i j} (t)$ denotes the static transmission error, and it is a displacement excitation in the same direction of $k_{i j}$ . The $e_{i j} (t)$ can be defined as:

7

e_{i j} (t) = e_{i j} s i n (Z_{i} Ω_{i} t),

where $e_{i j}$ denotes the amplitude of static transmission error (STE) of the gear pair $i j$ . $Z_{i}$ and $Ω_{i}$ denote the number of tooth and rotational speed of gear $i$ .

Substituting Eqs. (6) and (7) into Eq. (5), the equations of motion of the helical gear pair $i j$ are rewritten as follows:

8

M_{i j} {\ddot{X}}_{i j} + (C_{i j} + G_{i j}) {\dot{X}}_{i j} + K_{i j} X_{i j} = F_{i j} + F_{w},

where $M_{i j}$ , $C_{i j}$ , $G_{i j}$ and $K_{i j}$ denote the mass, damping, gyroscopic and mesh stiffness matrices of the gear pair $i j$ . $F_{i j}$ and $F_{w}$ are the excitation force vectors. And they can be expressed as:

9

M_{i j} = d i a g (m_{i}, m_{i}, m_{i}, I_{i x}, I_{i y}, I_{i z}, m_{j}, m_{j}, m_{j}, I_{j x}, I_{j y}, I_{j z}),

10

X_{i j} = [x_{i}, y_{i}, z_{i}, θ_{x i}, θ_{y i}, θ_{z i}, x_{j}, y_{j}, z_{j}, θ_{x j}, θ_{y j}, θ_{z j}]^{T},

11

K_{i j} = k_{i j} α_{i j}^{T} \cdot α_{i j},

12

C_{i j} = c_{i j} α_{i j}^{T} \cdot α_{i j},

13

F_{i j} = k_{i j} α_{i j}^{T} e_{i j} (t) + c_{i j} α_{i j}^{T} {\dot{e}}_{i j} (t),

14

F_{w} = [0,0, 0,0, 0, s g n T_{i}, 0,0, 0,0, 0, s g n T_{j}]^{T},

where $α_{i j}$ can be expressed as follows:

15

α_{i j} = [- s i n ψ_{i j} c o s β_{i j}, c o s ψ_{i j} c o s β_{i j}, s g n \times s i n β_{i j}, r_{b i} s i n ψ_{i j} s i n β_{i j}, - r_{b i} c o s ψ_{i j} s i n β_{i j},

s g n \times r_{b i} c o s β_{i j}, s i n ψ_{i j} c o s β_{i j}, - c o s ψ_{i j} c o s β_{i j}, - s g n \times s i n β_{i j},

r_{b j} s i n ψ_{i j} s i n β_{i j}, - r_{b j} c o s ψ_{i j} s i n β_{i j}, s g n \times r_{b j} c o s β_{i j}] .

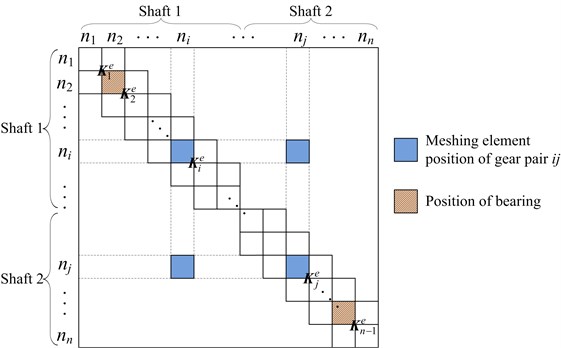
In Ref. [22], the shafts are simulated using Timoshenko beam elements, and some rigid disks on the shaft are simulated using lumped mass elements. By introducing the lumped mass models of gear pairs into the FE models of the shafts, equations of motions of the entire system can be expressed as:

16

M \ddot{u} + (C + G) \dot{u} + K u = F_{u},

where $M$ , $C$ , $K$ , $G$ and are the mass, damping, stiffness and gyroscopic matrices. $F_{u}$ is the external force vector of the system. Here, the stiffness matrix of bearing is expressed as $K_{b} = d i a g [k_{x x}, k_{y y}, k_{z z}, k_{θ x θ x}, k_{θ y θ y}, k_{θ z θ z}]$ . According to the position of bearings and gears, the bearing stiffness matrix and mesh stiffness matrix are added to the stiffness matrix of the shafts. As shown in Fig. 2, total stiffness matrix of system is assembled, in which only two shafts are di splayed. The Rayleigh-type damping is adopted in this study, which can be expressed as:

17

C = α M + β K,

where:

18

α = \frac{4 π f_{n 1} f_{n 2} (f_{n 2} ξ_{1} - f_{n 1} ξ_{2})}{(f_{n 2}^{2} - f_{n 1}^{2})},

19

β = \frac{(f_{n 2} ξ_{2} - f_{n 1} ξ_{1})}{π (f_{n 2}^{2} - f_{n 1}^{2})},

here, $f_{n 1}$ and $f_{n 2}$ denote the first-order and the second-order natural frequencies (Hz), respectively. In this paper, modal damping ratios $ξ_{1} = ξ_{2} =$ 0.04.

2.2. A new mathematical model of gear rotor system

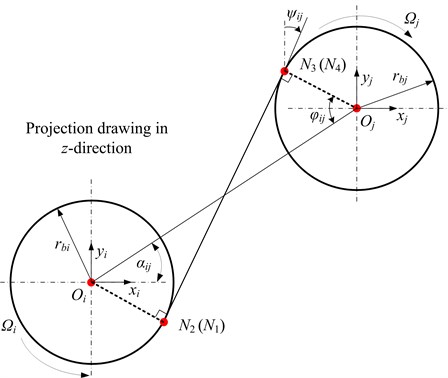
In this section, a new dynamic model is presented using FE method based on ANSYS software. Gear meshing is modeled as two lumped masses connecting by a liner spring, which is normal to the gear tooth contact surface, as shown in Figs. 1(b) and (d). According to the direction of the load, the direction of action plane changes. Here, a driving gear with counterclockwise rotation and left hand teeth is taken as a example, as shown in Figs. 1(b) and (d), in which the tangent lines $\bar{N_{1} N_{2}}$ and $\bar{N_{3} N_{4}}$ can be determined according to the geometrical relationship. The length between $N_{2}$ and $N_{3}$ can be calculated as (see Fig. 3):

20

\bar{N_{2} N_{3}} = \bar{O_{i} O_{j}} s i n φ_{i j} = (r_{b i} + r_{b j}) t a n φ_{i j} .

Fig. 2Schematic of the whole stiffness matrix

The length of $\bar{N_{1} N_{2}}$ and $\bar{N_{3} N_{4}}$ can be expressed as:

21

\bar{N_{1} N_{2}} = \bar{N_{3} N_{4}} = \bar{N_{2} N_{3}} t a n β_{i j} .

Considering the symmetry of the gears about $x y$ plane, $\bar{N_{1} N_{2}}$ and $\bar{N_{3} N_{4}}$ are divided into two equal parts $($ i.e. $\bar{C_{1} N_{1}} = \bar{C_{1} N_{2}}, \bar{C_{2} N_{3}} = \bar{C_{2} N_{4}})$ , as shown in Fig. 1d. The coordinates of $N_{1}$ and $N_{3}$ can be written as (see Fig. 3):

22

\{\begin{array}{l} N_{1 x} = O_{i x} + r_{b i} c o s ψ_{i j}, \\ N_{1 y} = O_{i y} + r_{b i} s i n ψ_{i j}, \\ N_{1 z} = O_{i z} - \bar{N_{1} N_{2}} / 2 = O_{i z} - (r_{b i} + r_{b j}) t a n φ_{i j} t a n β_{i j} / 2, \\ N_{3 x} = O_{j x} - r_{b j} c o s ψ_{i j}, \\ N_{3 y} = O_{j y} - r_{b j} s i n ψ_{i j}, \\ N_{3 z} = O_{j z} + \bar{N_{3} N_{4}} / 2 = O_{j z} + (r_{b i} + r_{b j}) t a n φ_{i j} t a n β_{i j} / 2, \end{array}

where, $N_{1 x}$ , $N_{1 y}$ , $N_{1 z}$ , $N_{3 x}$ , $N_{3 y}$ , $N_{3 z}$ , $O_{i x}$ , $O_{i y}$ , $O_{i z}$ , $O_{j x}$ , $O_{j y}$ and $O_{j z}$ denote the coordinates of $N_{1}$ , $N_{3}$ , $O_{i}$ and $O_{j}$ in $x$ , $y$ and $z$ directions. Once these coordinates are determined, the direction of spring can be defined, i.e., the meshing relation of two gears can be determined. Here, for the convenience of the modeling, $N_{1}$ and $N_{3}$ are selected as the ends of spring.

There are four working modes for the driving gear $i$ , i.e., counterclockwise rotation and left-hand teeth, counterclockwise rotation and right-hand teeth, clockwise rotation and left-hand teeth, clockwise rotation and right-hand teeth. Thus the positions of spring will change under different cases. However, these coordinates of the two ends of spring for the four cases can be expressed as:

23

\{\begin{array}{l} N_{i x} = O_{i x} + s g n r_{b i} c o s ψ_{i j}, \\ N_{i y} = O_{i y} + s g n r_{b i} s i n ψ_{i j}, \\ N_{i z} = O_{i z} - s g n (r_{b i} + r_{b j}) t a n φ_{i j} t a n β_{i j} / 2, \\ N_{j x} = O_{j x} - s g n r_{b j} c o s ψ_{i j}, \\ N_{j y} = O_{j y} - s g n r_{b j} s i n ψ_{i j}, \\ N_{j z} = O_{j z} + s g n (r_{b i} + r_{b j}) t a n φ_{i j} t a n β_{i j} / 2, \end{array}

where $N_{i x}$ , $N_{i y}$ , $N_{i z}$ , $N_{j x}$ , $N_{j y}$ and $N_{j z}$ denote the coordinates of the two ends of spring in $x$ , $y$ and $z$ directions, respectively.

In ANSYS software, the detailed modeling process is briefly introduced as follows (see Fig. 1(c)): (1) According to the physical dimensions of the shafts and the actual gear positions, the FE models of bearing-rotor systems including bearings, shafts, gears and rigid disks are established; (2) The coordinates of gears are determined, and then the coordinates of the two ends of the meshing spring are determined based on Eq. (23); (3) Rigid connections are established between the ends of meshing springs and gears by using the command “cerig”. Thus, the FE model of the whole gear rotor system will be established.

For the gear static transmission error excitations, it is loaded on both ends of meshing spring in an opposite direction along the direction of spring. And the excitation force due to the static transmission error $F_{e i j}$ can be written as:

24

{F_{e}}_{i j} = k_{i j} e_{i j} (t) + c_{i j} {\dot{e}}_{i j} (t) .

Fig. 3Projection drawing of Fig. 1(b) in z-direction

3. Model verification and discussion

In order to prove the validity of the present method, two gear rotor systems offered in Refs. [1, 9] are adopted. First of all, the present method will be verified by comparing the natural characteristics with those obtained using different methods in published literatures. Subsequently, the vibration responses obtained from present method and previous methods will be compared to verify the present method.

3.1. Model verification by comparing the natural characteristics

A spur gear rotor system is taken into account at first (see Fig. 4), and the parameters of system are listed in Table 1, which are offered in Refs. [9, 24]. Here, the effect of damping is ignored, and the helix angel $β_{i j}$ is equal to zero for the spur gear. The first 11 orders of natural frequencies calculated by present method are compared with the results of Ref. [9] (see Table 2). At the same time, the descriptions of the mode shapes based on the present method are also listed in Table 2. It is obvious that the frequencies obtained by present method agree well with those offered in Ref. [9] except for some higher modes, and the relative error is less than 3.31 %.

Table 1Parameters of the gear system

Gear parameters
Gear	$I_{x} = I_{y}$ (kg·m²)	$I_{z}$ (kg·m²)		$m$ (kg)	Base circle radius (m)			Tooth number	$k_{m}$ (N/m)
1	0.0009	0.0018		1.84	0.0445			28	1×10⁸
2	0.0009	0.0018		1.84	0.0445			28
Bearing parameters
Bearing	$k_{x x}$					$k_{y y}$
All	1×10⁹					1×10⁹
Material parameters
Modulus of elasticity (GPa)			Density of material (kg/m³)				Poisson’s ratio
207.8			7806.0				0.3

Fig. 4Schematic of the spur gear rotor system [9]

Table 2Natural frequencies of the spur gear rotor system

Mode no.	Natural frequencies (Hz)		Relative errors	Mode description
Mode no.	Present method	Ref. [9]	Relative errors	Mode description
$f_{n 1}$	572.61	581	1.44 %	Coupled lateral-torsional vibration
$f_{n 2}$	678.68	687	1.21 %	1st lateral, $y$ -direction, driving shaft
$f_{n 3}$	679.64	689	1.36 %	Coupled lateral- torsional vibration
$f_{n 4}$	680.61	691	1.50 %	1st lateral, $y$ -direction, driven shaft
$f_{n 5}$	2513.4	2524	0.42 %	Coupled lateral-torsional vibration
$f_{n 6}$	3371.0	3387	0.47 %	2nd lateral, $x$ -direction, driving shaft
$f_{n 7}$	3371.0	3387	0.47 %	2nd lateral, $y$ -direction, driving shaft
$f_{n 8}$	3395.3	3421	0.75 %	2nd lateral, $y$ -direction, driven shaft
$f_{n 9}$	3395.4	3421	0.75 %	2nd lateral, $x$ -direction, driven shaft
$f_{n 10}$	6322.3	6447	1.93 %	Torsional, $z$ -direction, driving shaft
$f_{n 11}$	6322.3	6539	3.31 %	Torsional, $z$ -direction, driven shaft

In this section, a two-stage helical gear rotor system offered in Ref. [1] is taken for further comparison, as shown in Fig. 1(a). Here, the example system with $α_{12} =$ 0 and $α_{34} =$ 0 is considered, and the detailed parameters of the system and the STE of gear can be found in Ref. [2]. The lumped mass values and the material parameters, which are not provided in Ref. [1], can be found in Ref. [22]. The natural frequencies are calculated using Zhang’s method and present method, as listed in Table 3. In addition, the typical mode shapes obtained from two methods are shown in Fig. 5, which shows that the natural frequencies and mode shapes obtained from the present method agree well with those obtained from Zhang’s method, and the maximum relative error of natural frequency is less than 2.17 % (see Table 3).

Fig. 5Partial mode shapes: a) fn1, b) fn2, c) fn3, d) fn4, e) fn5, f) fn7, g) fn9

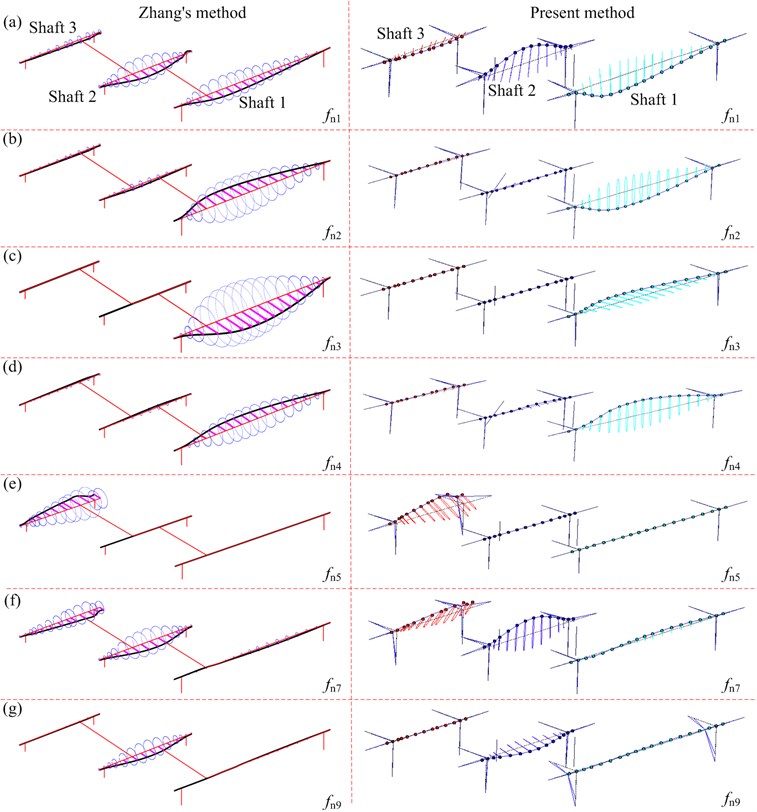
Fig. 6Mode shape corresponding to 812 Hz in Ref. [1]

In Ref. [1], only a mode shape corresponding to 812 Hz is provided, as shown in Fig. 6. This mode corresponds to the first non-rigid mode $f_{n 1}$ in present method. It is clear that the natural frequencies and mode shapes obtained by present method also show a good agreement with those provided in Ref. [1]. These comparisons show that the present model is effective to calculate the natural characteristics of the geared rotor systems.

Table 3Natural frequencies of the helical gear rotor system

Mode No.	Natural frequencies (Hz)		Relative errors
Mode No.	Present method (Hz)	Zhang’s method (Hz)	Relative errors
$f_{n 1}$	808.49	806.84	–0.2 %
$f_{n 2}$	1357.05	1337.42	–1.47 %
$f_{n 3}$	1468.04	1543.27	–1.02 %
$f_{n 4}$	1658.66	1669.46	0.65 %
$f_{n 5}$	2334.52	2321.96	–0.54 %
$f_{n 6}$	2349.00	2345.32	–0.16 %
$f_{n 7}$	2368.75	2364.55	–0.18 %
$f_{n 8}$	2553.83	2545.12	–0.34 %
$f_{n 9}$	2656.51	2657.08	0.02 %
$f_{n 10}$	2845.74	2859.26	0.47 %
$f_{n 11}$	2988.27	3054.63	2.17 %
$f_{n 12}$	3045.66	3060.67	0.49 %
$f_{n 13}$	3287.33	3262.50	–0.76 %
$f_{n 14}$	3338.58	3268.07	–2.16 %
$f_{n 15}$	3749.98	3785.57	0.94 %

3.2. Model verification by comparing the vibration responses

In this section, the present dynamic model is further verified by comparing the vibration responses with those in Refs. [1, 2] and Zhang’s method [22]. Considering the excitation force due to the static transmission error (Eq. (24)), $F_{12}$ (meshing force of gear pair 12) and $F_{34}$ (meshing force of gear pair 34) are calculated using the present method, and they are also compared with the results in Ref. [2] (see Fig. 7). In the figure, $f_{e 12}$ and $f_{e 34}$ denote the meshing frequencies of gear pairs 12 and 34. The figure shows that two peaks ( $f_{e 12} = f_{n 1}$ and $f_{e 34} = f_{n 1}$ ) obtained from the present method agree well with those in Ref. [2], however, there are some errors for other peaks. Some reasons may lead to these errors as follows: 1) Some geometric parameters may be different because of the lack in Ref. [2], and some parameters of system are adopted by referring to the Ref. [22]. 2) The torque and other working condition are not provided in Ref. [2].

Fig. 7Dynamic meshing forces: a) gear pair 12, b) gear pair 34

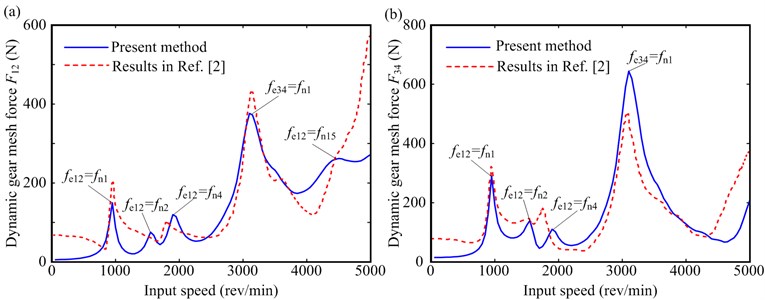
Fig. 8Gear meshing force amplitudes and maximum values under T= 50 Nm: a) meshing force amplitude of F12, b) maximum values of F12, c) meshing force amplitude of F34, d) maximum values of gear pair F34

Gear meshing force amplitudes and maximum values under T= 50 Nm: a) meshing force amplitude of F12, b) maximum values of F12, c) meshing force amplitude of F34, d) maximum values of gear pair F34

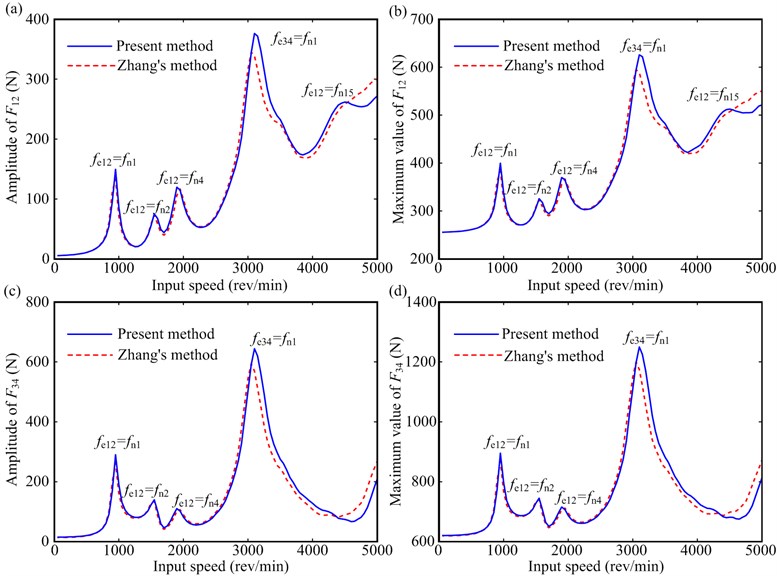
Fig. 9Vibration responses under T= 100 Nm: a) y-direction responses of gear 1; b) θz-direction responses of gear 1; c) y-direction responses of gear 2; d) θz-direction responses of gear 2

Vibration responses under T= 100 Nm: a) y-direction responses of gear 1; b) θz-direction responses of gear 1; c) y-direction responses of gear 2; d) θz-direction responses of gear 2

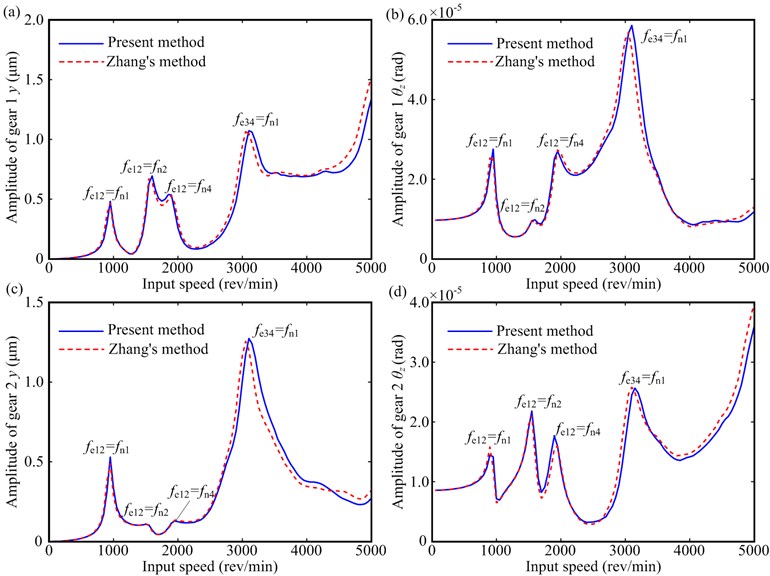
Vibration responses of the helical gear rotor system under $T =$ 50 Nm and 100 Nm are shown in Figs. 8, 9 and 10, respectively. These figures show the following dynamic characteristics:

(1) Meshing forces, vibration displacements, and frequency components obtained from the present method agree well with those obtained from Zhang's method under lower frequency regions, and there exist slight errors under higher frequency regions (see Figs. 8 and 9). The main reason of the slight error may be that some high order terms due to the lateral-torsional-axial-swing coupling of gear pairs are ignored for Zhang’s method.

(2) The resonant peaks of the rotor system appear under $f_{e 12} = f_{n 1}$ , $f_{n 2}$ , $f_{n 4}$ , $f_{n 15}$ and $f_{e 34} = f_{n 1}$ (see Table 3), which are primary members of the lateral-torsional coupling vibration (see Fig. 5). For these modes, the vibration of shaft 1 is dominated (see Fig. 5), and the vibration mode at the first natural frequency $f_{n 1}$ is easily excited (see Figs. 8 and 9).

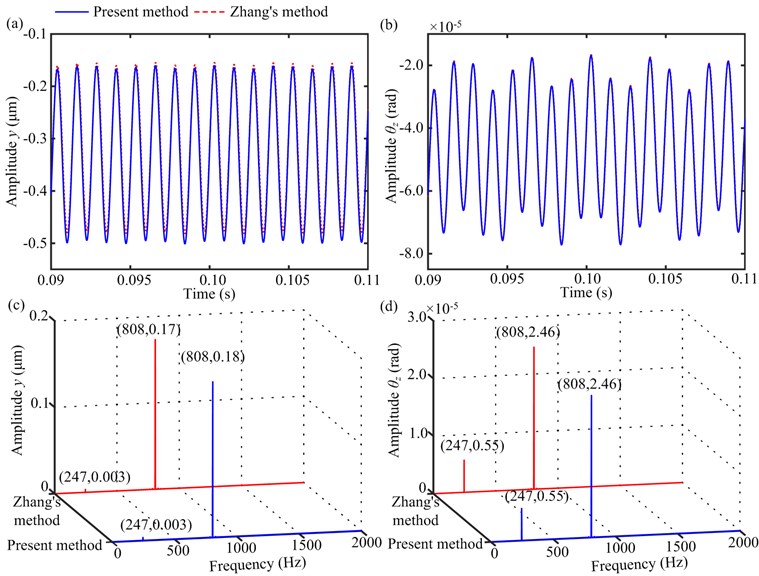
(3) The vibration responses at $Ω_{1} =$ 932 rev/min show that two meshing frequencies of the gear pairs 12 and 34 (808 Hz and 247 Hz) can be observed (see Fig. 10). The amplitude at meshing frequency of 808 Hz is dominated because the meshing frequency coincides with $f_{n 1}$ . In addition, the torsional vibration is easily excited relative to the lateral vibration (see Fig. 10).

Fig. 10Vibration responses of gear 4 under T= 50 Nm and Ω1= 932 rev/min: a) time-domain waveforms in y-direction, b) time-domain waveforms in θz-direction, c) amplitude spectra in y-direction, d) amplitude spectra in θz-direction

Vibration responses of gear 4 under T= 50 Nm and Ω1= 932 rev/min: a) time-domain waveforms in y-direction, b) time-domain waveforms in θz-direction, c) amplitude spectra in y-direction, d) amplitude spectra in θz-direction

4. Conclusions

In ANSYS software, a new finite element model for general helical gear rotor systems is presented taking the lateral-torsional-axial-swing coupling due to helical gear pairs into account. The proposed method is validated by comparing the natural characteristics and vibration responses with those obtained from the published references and Zhang’s method. Main conclusions are listed as follows:

1) The proposed method can easily deal with the meshing relation of gear pairs by conveniently calculating the displacement of the meshing spring. The new method not only has a good calculation accuracy, but also can greatly reduce the difficulty of programming relative to the conventional method, such as Kubur’s method [1, 2] and Zhang’s method [6].

2) For the studied geared rotor system provided in Ref. [2], the results show that the first-, second- and fourth-order natural frequencies are more easily excited, especially the first natural frequency. In addition, for the studied geared rotor system, the torsional vibration is easily excited relative to the lateral vibration at a low rotational speed.

References

Kubur M., Kahraman A., Zini D. M., et al. Dynamic analysis of multi-mesh helical gear sets by finite elements. ASME 2003 International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, American Society of Mechanical Engineers, Chicago, USA, 2003, p. 333-343.

Publisher
Kubur M., Kahraman A., Zini D. M., et al. Dynamic analysis of a multi-shaft helical gear transmission by finite elements: model and experiment. Journal of Vibration and Acoustics, Vol. 126, Issue 3, 2004, p. 398-406.

Publisher
Ma H., Zeng J., Feng R., et al. Review on dynamics of cracked gear systems. Engineering Failure Analysis, Vol. 55, 2015, p. 224-245.

Publisher
Iida H., Tamura A., Kikuchi K., et al. Coupled torsional-flexural vibration of a shaft in a geared system of rotors: 1st report. Bulletin of JSME, Vol. 23, Issue 186, 1980, p. 2111-2117.

Publisher
Choy F. K., Tu Y. K., Zakrajsek J. J., et al. Effects of gear box vibration and mass imbalance on the dynamics of multistage gear transmission. Journal of Vibration and Acoustics, Vol. 113, Issue 3, 1991, p. 333-344.

Publisher
Kahraman A., Singh R. Interactions between time-varying mesh stiffness and clearance non-linearities in a geared system. Journal of Sound and Vibration, Vol. 146, Issue 1, 1991, p. 135-156.

Publisher
Lim T. C., Singh R. Vibration transmission through rolling element bearings. Part III: Geared rotor system studies. Journal of Sound and Vibration, Vol. 151, Issue 1, 1991, p. 31-54.

Publisher
Özgüven H. N. A non-linear mathematical model for dynamic analysis of spur gears including shaft and bearing dynamics. Journal of Sound and Vibration, Vol. 145, Issue 2, 1991, p. 239-260.

Publisher
Kahraman A., Ozguven H. N., Houser D. R., et al. Dynamic analysis of geared rotors by finite elements. Journal of Mechanical Design, Vol. 114, Issue 3, 1992, p. 507-514.

Publisher
Rao J. S., Shiau T. N., Chang J. R. Theoretical analysis of lateral response due to torsional excitation of geared rotors. Mechanism and Machine Theory, Vol. 33, Issue 6, 1998, p. 761-783.

Publisher
Jia S., Howard I., Wang J. The dynamic modeling of multiple pairs of spur gears in mesh, including friction and geometrical errors. International Journal of Rotating Machinery, Vol. 9, Issue 6, 2003, p. 437-442.

Publisher
Lee A. S., Ha J. W., Choi D. H. Coupled lateral and torsional vibration characteristics of a speed increasing geared rotor-bearing system. Journal of Sound and Vibration, Vol. 263, Issue 4, 2003, p. 725-742.

Publisher
Ma H., Pang X., Feng R., et al. Evaluation of optimum profile modification curves of profile shifted spur gears based on vibration responses. Mechanical Systems and Signal Processing, Vols. 70-71, 2016, p. 1131-1149.

Publisher
Ma H., Pang X., Feng R., et al. Fault features analysis of cracked gear considering the effects of the extended tooth contact. Engineering Failure Analysis, Vol. 48, 2015, p. 105-120.

Publisher
Ma H., Song R., Pang X., et al. Fault feature analysis of a cracked gear coupled rotor system. Mathematical Problems in Engineering, Vol. 2014, 2014, p. 1-22.

Publisher
Ma H., Yang J., Song R., et al. Effects of tip relief on vibration responses of a geared rotor system. Proceedings of the Institution of Mechanical Engineers Part C: Journal of Mechanical Engineering Science, Vol. 228, Issue 7, 2014, p. 1132-1154.

Publisher
Ma H., Pang X., Zeng J., et al. Effects of gear crack propagation paths on vibration responses of the perforated gear system. Mechanical Systems and Signal Processing, Vol. 62, 2015, p. 113-128.

Publisher
Blankenship G. W., Singh R. A new gear mesh interface dynamic model to predict multi-dimensional force coupling and excitation. Mechanism and Machine Theory, Vol. 30, Issue 1, 1995, p. 43-57.

Publisher
Velex P., Maatar M. A mathematical model for analyzing the influence of shape deviations and mounting errors on gear dynamic behavior. Journal of Sound and Vibration, Vol. 191, Issue 5, 1996, p. 629-660.

Publisher
Choi S. H., Glienicke J., Han D. C., et al. Dynamic gear loads due to coupled lateral, torsional and axial vibrations in a helical geared system. Journal of Vibration and Acoustics, Vol. 121, Issue 2, 1999, p. 141-148.

Publisher
Baud S., Velex P. Static and dynamic tooth loading in spur and helical geared systems-experiments and model validation. Journal of Mechanical Design, Vol. 124, Issue 2, 2002, p. 334-346.

Publisher
Zhang Y. M., Wang Q. B., Ma H., et al. Dynamic analysis of three-dimensional helical geared rotor system with geometric eccentricity. Journal of Mechanical Science and Technology, Vol. 27, Issue 11, 2013, p. 3231-3242.

Publisher
Zhang H., Zhai J. Y., Han Q. K., et al. Dynamics of a geared parallel-rotor system subjected to changing oil-bearing stiffness due to external loads. Finite Elements in Analysis and Design, Vol. 106, 2015, p. 32-40.

Publisher
Choi S. T., Mau S. Y. Dynamic analysis of geared rotor-bearing systems by the transfer matrix method. Journal of Mechanical Design, Vol. 123, Issue 4, 2001, p. 562-568.

Publisher

Cited by

A novel method for helical gear modeling with an experimental validation

Roee Cohen | Lior Bachar | Omri Matania | Renata Klein | Jacob Bortman

(2024)

Development of Dynamic Model to Predict Three-dimensional Vibrations of Helical Gear Pair

Ma Ru Kang

(2021)

Development of Shaft Analysis Model for Power Transmission System Optimization

Ju-Yeon Lee | Su-Chul Kim

(2021)

A Coupled Torsional-Transition Nonlinear Vibration and Dynamic Model of a Two-Stage Helical Gearbox Reducer for Electric Vehicles

Abdulhameed M. Y. Al-Tayari | Siyu Chen | Zhou Sun

(2020)

About this article

Received

01 September 2016

Accepted

14 October 2016

Published

15 February 2017

SUBJECTS

Mechanical vibrations and applications

DOI

https://doi.org/10.21595/jve.2016.17649

Keywords

dynamic model

helical gear

finite element

vibration responses

Acknowledgements

This Project is funded by the Aeronautical Science Foundation of China (Grant No. 201404Q5001). This support is gratefully acknowledged.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 12 30

Dynamics model and vibrational response analysis of helical gear-rotor-bearing transmission system

Hongyuan Zhang, Shuo Li, Xin Zhang

Research article

2023 12 28

Static transmission error measurement of various gear-shaft systems by finite element analysis

Alexander Czakó, Kamil Řehák, Aleš Prokop, Jakub Rekem, Daniel Láštic, Miroslav Trochta

Research article

2020 12 07

Determination of static transmission error of helical gears using finite element analysis

Alexander Czakó, Kamil Řehák, Aleš Prokop, Vinayak Ranjan

Research article

2019 05 15

Joint parameter identification, vibration and noise analysis of gearbox

Tengjiao Lin, Daokun Xie, Quancheng Peng, Songling Guo, Hesheng Lv

M. Yan and H.- Liu, “A dynamic modeling method for helical gear systems,” Journal of Vibroengineering, Vol. 19, No. 1, pp. 111–124, Feb. 2017, https://doi.org/10.21595/jve.2016.17649

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2016.17649
UR  - https://doi.org/10.21595/jve.2016.17649
TI  - A dynamic modeling method for helical gear systems
T2  - Journal of Vibroengineering
AU  - Yan, Ming
AU  - Liu, Hong-quan
PY  - 2017
DA  - 2017/02/15
PB  - JVE International Ltd.
SP  - 111-124
IS  - 1
VL  - 19
SN  - 1392-8716
ER  - 

Copy Ris

Copied to clipboard!

@article{Yan_2017,
	doi = {10.21595/jve.2016.17649},
	url = {https://doi.org/10.21595/jve.2016.17649},
	year = 2017,
	month = {feb},
	publisher = {{JVE} International Ltd.},
	volume = {19},
	number = {1},
	pages = {111--124},
	author = {Ming Yan and Hong-quan Liu},
	title = {A dynamic modeling method for helical gear systems},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]M. Yan and H. Liu, “A dynamic modeling method for helical gear systems,” Journal of Vibroengineering, vol. 19, no. 1, pp. 111–124, Feb. 2017, doi: 10.21595/jve.2016.17649.

Copy IEEE

Copied to clipboard!

Yan, Ming, and Hong-quan Liu. “A Dynamic Modeling Method for Helical Gear Systems.” Journal of Vibroengineering 19, no. 1 (February 15, 2017): 111–24. https://doi.org/10.21595/jve.2016.17649.

Copy Chicago

Copied to clipboard!

A dynamic modeling method for helical gear systems

Abstract

1. Introduction

2. Dynamic models of geared rotor systems

2.1. Dynamic models of geared rotor systems using Zhang’s method

2.2. A new mathematical model of gear rotor system

3. Model verification and discussion

3.1. Model verification by comparing the natural characteristics

3.2. Model verification by comparing the vibration responses

4. Conclusions

References

Cited by

About this article

Related Articles