Dynamic analysis of localized defects in rolling bearing systems

Song, Mengmeng; Xiao, Shungen; Huang, Lixia; Li, Wanxiang

doi:10.21595/vp.2017.18914

Vibroengineering Procedia

Browse Procedia

Published: 21 October 2017

Check for updates

Dynamic analysis of localized defects in rolling bearing systems

Mengmeng Song¹

Shungen Xiao²

Lixia Huang³

Wanxiang Li⁴

^{1, 2, 3, 4}College of Information, Mechanical and Electrical Engineering, Ningde Normal University, Ningde, People’s Republic of China

²School of Mechatronical Engineering and Automation, Shanghai University, Shanghai, People’s Republic of China

Corresponding Author:

Shungen Xiao

Cite the article Download PDF

Downloads 1632

CrossRef Citations 1

Abstract

In this paper, the dynamics of rolling bearing with localized defects of the outer ring and rolling element are investigated. In order to study the nonlinear dynamical behaviors of the rolling bearing precisely, a novel dynamic model of the rolling bearing is established based on the Lagrangian approach. By setting 0.2 mm, 0.4 mm and 0.6 mm local defects on the outer ring and rolling element of bearing respectively, the results demonstrate that the amplitude of the rolling bearing is more intense as the local defect size increases, and the acceleration amplitude fluctuation is more significant than the velocity. In addition, in the case of the same defect size, the vibration of the rolling element defect is more intense than the vibration response caused by the outer ring defect.

1. Introduction

Rolling bearings are an important part of the mechanical system, widely used in automobiles, ships and aircraft and other large mechanical systems. They have a great influence on the dynamic behavior of the rotating machines and act as a source of vibration and noise in these systems [1, 2]. Therefore, the surface detection and diagnosis for the rolling bearing systems are one of valuable works for industrial maintenance. Although various detection and diagnosis methods have been presented for the rolling bearing systems, modeling and simulation methods are one of accurate approaches for predicting the dynamic performance of the rolling bearing systems [2, 3], especially for the vibration characteristics caused by the surface defects [4].

In the past few decades, most studies have focused on the fault diagnosis method of rolling bearing systems with signal processing. For instance, Jiang et al. [5] studied rolling bearing fault identification using multilayer deep learning convolutional neural network. Ding et al. [6] presented fault diagnosis of rolling bearing based on improved CEEMDAN and distance evaluation technique. In recent years, A lot of research works have been conducted to dynamic behaviors for rolling bearings. For example, He et al. [7] introduced the nonlinear impact behaviors with the vibration force increasing, when the vibration frequency is determined. In their research, they established the piecewise non-smooth experiment model of three-degree-of-freedom rolling bearing system with fault in inner ring, and used the experiment method to further reveal the bifurcations and chaos of bearing system through establishing the Poincaré mapping on the collision plane. Cao et al. [8] developed a dynamic model to investigate vibrations of high speed rolling ball bearings with localized surface defects on raceways. Liu et al. [9] studied the impulse vibration transmission through the deep groove ball bearing systems caused by a localized surface defect on the bearing raceways. Sopanen et al. [10] proposed dynamic model of a deep-groove ball bearing including localized and distributed defects with six degrees of freedom. Kıral et al. [11] investigated the vibration analysis of rolling element bearings with various defects under the action of an unbalanced force. Patil et al. [12] presented a theoretical model to predict the effect of localized defect on vibrations associated with ball bearing.

Based on the research results of the previous description, the main purpose of this study is to conduct a study based on dynamic response of rolling bearing with localized defects. The paper is organized as follows: The dynamic model of rolling bearing with surface defects is established in Section 2. The dynamic response of outer ring and rolling element defects are discussed in Section 3, respectively. In the end, the conclusions of this paper are given in Section 4.

2. System model of surface defects in rolling bearing

It is assumed that the rolling bearing rotates at a steady speed, the friction generated during the rotation of the bearing is overcome, regardless of the elastic deformation of the component, the rolling element is in close contact with the raceway, the gap is changed, the system potential is constant, the influence of lubricating oil can be ignored. The nonlinear dynamic equation of rolling bearing is established. The angle between the $z'$ -axis of the rolling element and the center of the bearing in the $z$ -axis direction is $χ$ , the angle between the $y'$ axis of the rolling element and the $y$ -axis direction of the bearing center is $β$ , and the two generalized coordinates are $q_{1} = χ$ , $q_{2} = β$ , respectively, as shown in Fig. 1. Two sets of Cartesian coordinate systems are established respectively on the rolling bearing, namely, the bearing center coordinate system $O x y z$ and the ball center coordinate system $O' x' y' z'$ . In the bearing center coordinate system $O x y z$ , the origin $O$ of the bearing center coordinate system is the rotation center of the bearing outer ring, the inner ring and the cage, the $x$ axis is the rotation axis, and $z$ axis is the vertical direction. In the ball center coordinate system $O' x' y' z'$ , the center of the ball coordinate system is the center of the ball, $x'$ and $x$ are parallel, $y'$ axis is along the direction of the ball movement, $z'$ axis is located in the center of the bearing and ball center connection.

Fig. 1The dynamic analysis diagram of deep groove ball bearing ball

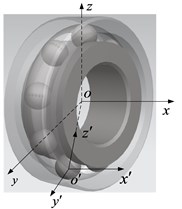
According to the principle of moment of inertia, it is not difficult to find the moment of inertia of the outer ring, inner ring and rolling element, respectively, as follows:

1

J_{o} = \frac{m_{o}}{2} [R_{o}^{2} + {(R_{o} - b)}^{2}], J_{i} = \frac{m_{i}}{2} [R_{i}^{2} + {(R_{i} - b)}^{2}], J_{j} = m [{(R_{i} + r)}^{2} + \frac{3}{4} r^{2}],

where $m_{o}$ , $m_{i}$ and $m$ represent the mass of the outer ring, the inner ring and the rolling element of the rolling bearing, respectively. The inner and outer ring thicknesses are $b$ , the ball radius is $r$ . $R_{o}$ and $R_{i}$ represent the radius of the outer ring and the inner ring of the rolling bearing respectively, $J_{o}$ , $J_{i}$ and $J_{j}$ represent the moment of inertia outer ring, inner ring and rolling element of rolling bearing, respectively.

According to the kinetic energy formula, the kinetic energy of rolling bearing, inner ring and outer ring can be respectively written as:

2

E_{j} = \frac{1}{2} m ({\dot{x}}_{j}^{2} + {\dot{y}}_{j}^{2}) + \frac{1}{2} J_{j} {\dot{ψ}}_{j}^{2},

where $E_{j}$ is expressed as the kinetic energy of the $j$ -th rolling element. $x_{j}$ and $y_{j}$ represent the coordinate positions of the $j$ -th rolling center, $ψ_{j}$ represents the angular displacement of the $j$ -th rolling element, and $J_{j}$ represent the moment of inertia of rolling element:

3

E_{n} = \sum_{j = 1}^{n} E_{j} = \sum_{j = 1}^{n} [\frac{1}{2} m ({\dot{x}}_{j}^{2} + {\dot{y}}_{j}^{2}) + \frac{1}{2} J_{j} {\dot{ψ}}_{j}^{2}],

where $E_{n}$ is the sum of the kinetic energy of all rolling elements:

4

E_{i} = \frac{1}{2} m ({\dot{x}}_{i}^{2} + {\dot{y}}_{i}^{2}) + \frac{1}{2} J_{i} {\dot{ψ}}_{i}^{2},

where $E_{i}$ is expressed as the kinetic energy of the inner ring of the rolling bearing, $x_{i}$ and $y_{i}$ represent the coordinate position of the center of the inner circle, and $J_{i}$ denotes the moment of inertia of inner ring.

The kinetic energy of the outer ring of the rolling bearing can be determined using the following formula:

5

E_{o} = \frac{1}{2} m ({\dot{x}}_{o}^{2} + {\dot{y}}_{o}^{2}) + \frac{1}{2} J_{o} {\dot{ψ}}_{o}^{2} .

In which, $E_{o}$ is expressed as the kinetic energy of the outer ring of the rolling bearing, $x_{o}$ and $y_{o}$ represent the coordinate position of the outer center, $ψ_{o}$ represents the angular displacement of the outer ring, and $J_{o}$ represent the moment of inertia of outer ring.

The sum of the kinetic energy of the outer ring, the inner ring and the rolling element of the rolling bearing can be deduced as follow:

6

E = \sum_{j = 1}^{n} E_{j} + E_{i} + E_{o} = \frac{1}{2} (J_{11} {\dot{q}}_{1}^{2} + J_{12} {\dot{q}}_{2}^{2}) + \frac{1}{2} (J_{21} {\dot{q}}_{1}^{2} + J_{22} {\dot{q}}_{2}^{2}) + \frac{1}{2} (J_{31} {\dot{q}}_{1}^{2} + J_{32} {\dot{q}}_{2}^{2}),

J_{11} = \sum_{j = 1}^{2} \{m [{(u_{x j}^{(1)})}^{2} + {(u_{y j}^{(1)})}^{2}] + J_{j} {(u_{ψ j}^{(1)})}^{2}\},

J_{12} = \sum_{j = 1}^{2} \{m [{(u_{x j}^{(2)})}^{2} + {(u_{y j}^{(2)})}^{2}] + J_{j} {(u_{ψ j}^{(2)})}^{2}\},

J_{21} = m_{i} [{(u_{x i}^{(1)})}^{2} + {(u_{y i}^{(1)})}^{2}] + J_{i} {(u_{ψ i}^{(1)})}^{2}, J_{22} = m_{i} [{(u_{x i}^{(2)})}^{2} + {(u_{y i}^{(2)})}^{2}] + J_{i} {(u_{ψ i}^{(2)})}^{2},

J_{31} = m_{o} [{(u_{x o}^{(1)})}^{2} + {(u_{y o}^{(1)})}^{2}] + J_{o} {(u_{ψ o}^{(1)})}^{2}, J_{32} = m_{o} [{(u_{x o}^{(2)})}^{2} + {(u_{y o}^{(2)})}^{2}] + J_{o} {(u_{ψ o}^{(2)})}^{2},

where $u_{k j}^{(i)}$ denotes the partial velocity of the $j$ -th ball to $i$ -th generalized coordinates, $u_{k i}^{(i)}$ denotes the partial velocity of the inner circle to $i$ -th generalized coordinates, $u_{k o}^{(i)}$ denotes the partial velocity of the outer circle to $i$ -th generalized coordinates. $k$ represent $x$ , $y$ and $z$ . $J_{11}$ , $J_{12}$ , $J_{21}$ , $J_{22}$ , $J_{31}$ , $J_{32}$ are expressed as the equivalent moment of inertia. Because they are related to partial velocity, they are usually $q_{1}$ and $q_{2}$ function.

Substituting Eq. (6) into the Laplace equation:

7

\frac{\partial E}{\partial {\dot{q}}_{i}} = J_{1 i} {\dot{q}}_{i} + J_{2 i} {\dot{q}}_{i} + J_{3 i} {\dot{q}}_{i}, (i = 1,2),

8

\frac{d}{d t} (\frac{\partial E}{\partial {\dot{q}}_{i}}) = J_{11} {\ddot{q}}_{i} + \frac{\partial J_{1 i}}{\partial q_{i}} {\dot{q}}_{1}^{2} + \frac{\partial J_{1 i}}{\partial q_{i}} {\dot{q}}_{1} {\dot{q}}_{2} + {\ddot{q}}_{i} J_{2 i} + \frac{\partial J_{2 i}}{\partial q_{i}} {\dot{q}}_{i}^{2}

+ \frac{\partial J_{2 i}}{\partial q_{i}} {\dot{q}}_{1} {\dot{q}}_{2} + J_{31} {\dot{q}}_{i}^{2} + \frac{\partial J_{3 i}}{\partial q_{i}} {\dot{q}}_{i}^{2} + \frac{\partial J_{3 i}}{\partial q_{i}} {\dot{q}}_{1}^{} {\dot{q}}_{2}, (i = 1,2),

9

\frac{\partial E}{\partial q_{i}} = \frac{1}{2} (\frac{\partial J_{11}}{\partial q_{i}} {\dot{q}}_{1}^{2} + \frac{\partial J_{12}}{\partial q_{i}} {\dot{q}}_{2}^{2}) + \frac{1}{2} (\frac{\partial J_{21}}{\partial q_{i}} {\dot{q}}_{1}^{2} + \frac{\partial J_{22}}{\partial q_{i}} {\dot{q}}_{2}^{2}) + \frac{1}{2} (\frac{\partial J_{31}}{\partial q_{i}} {\dot{q}}_{1}^{2} + \frac{\partial J_{32}}{\partial q_{i}} {\dot{q}}_{2}^{2}), (i = 1,2) .

It is supposed that the external force $p$ -th and the external torque $l$ -th are applied to the rolling bearing, the potential energy $U$ is constant and the number of the roller pressed is equal to the number of external forces, so the generalized force $Q_{1}$ and $Q_{2}$ to the coordinate $i$ can be expressed as follow:

10

Q_{j} = \sum_{i = 1}^{l} (F_{i x} u_{x i}^{(j)} + F_{i y} u_{y i}^{(j)}) + \sum_{i = 1}^{l} M_{i} u_{ψ i}^{(j)}, (j = 1, 2),

where $F_{i x}$ and $F_{i y}$ represent the components of the $i$ -th external force in the $x$ and $y$ direction, respectively.

Lagrange motion equation for an unconstrained dynamical system is as follows:

11

\frac{d}{d t} (\frac{\partial E}{\partial {\dot{q}}_{j}}) - \frac{\partial E}{\partial q_{j}} + \frac{\partial U}{\partial q_{j}} = Q_{j}, (j = 1, 2),

where $E$ and $U$ are the system kinetic and potential energies, respectively.

Substituting Eqs. (7)-(10) into Eq. (11), the nonlinear dynamic equation of the rolling bearing can be written as:

12

\{\begin{array}{l} (J_{1 i} + J_{2 i} + J_{3 i}) {\ddot{q}}_{i} + \frac{1}{2} (\frac{\partial J_{1 i}}{\partial q_{i}} + \frac{\partial J_{2 i}}{\partial q_{i}} + \frac{\partial J_{3 i}}{\partial q_{i}}) {\dot{q}}_{i}^{2} + (\frac{\partial J_{1 i}}{\partial q_{i}} + \frac{\partial J_{2 i}}{\partial q_{i}} + \frac{\partial J_{3 i}}{\partial q_{i}}) {\dot{q}}_{1} {\dot{q}}_{2} \\ - \frac{1}{2} (\frac{\partial J_{12}}{\partial q_{i}} + \frac{\partial J_{22}}{\partial q_{i}} + \frac{\partial J_{32}}{\partial q_{i}}) {\dot{q}}_{2}^{2} = Q_{1}, \\ (J_{12} + J_{22} + J_{32}) {\ddot{q}}_{2} + \frac{1}{2} (\frac{\partial J_{12}}{\partial q_{2}} + \frac{\partial J_{22}}{\partial q_{2}} + \frac{\partial J_{32}}{\partial q_{2}}) {\dot{q}}_{2}^{2} + (\frac{\partial J_{12}}{\partial q_{2}} + \frac{\partial J_{22}}{\partial q_{2}} + \frac{\partial J_{32}}{\partial q_{2}}) {\dot{q}}_{1} {\dot{q}}_{2} \\ - \frac{1}{2} (\frac{\partial J_{11}}{\partial q_{2}} + \frac{\partial J_{21}}{\partial q_{2}} + \frac{\partial J_{31}}{\partial q_{2}}) {\dot{q}}_{1}^{2} = Q_{2} . \end{array}

3. Dynamic responses results and discuss

In this section, the dynamic responses of rolling bearing with outer ring defects and rolling element are researched. The simulation results show that the localized defects of the outer ring and rolling element will affect the dynamic performance of the rolling bearing. In the simulation, select the model of 6307 deep groove ball bearings as the object of study, set the radius of 1.5 mm for the ball. The outer ring is fixed, the speed of inner ring is set to 3000 r/min. The radius of the localized defect is set to 0.2 mm, 0.4 mm and 0.6 mm respectively, the bearing is subjected to an axial load of 3000 N and a radial load of 2000 N.

The velocity, and acceleration of the outer ring without/with 0.2 mm, 0.4 mm and 0.6 mm defects are shown in Figs. 2 to 4, respectively. It is can be seen from Figs. 2 to 4, with the rolling bearing outer ring defect size increases, the velocity and acceleration of the system have a significant effect in $x$ and $y$ directions. Compared with the non-defective rolling bearing dynamic response, when the outer ring defects from 0.2 mm to 0.6 mm, the maximal value of the velocity in $x$ direction increases from 0.012 mm/s to 0.026 mm/s, the maximal value of the velocity in y direction increases from 0.014 mm/s to 0.030 mm/s, the maximal peak value of outer ring acceleration increases in $x$ direction from 54.77 mm/s²to 1163 mm/s², and the maximal peak value of outer ring acceleration increases in $y$ direction from 52.57 mm/s²to 613.4 mm/s². Obviously, whether in the $x$ direction or $y$ direction, the outer ring defects have a greater impact on the acceleration than the velocity.

Acceleration of the rolling element with 0.2 mm, 0.4 mm and 0.6 mm defects are shown in Fig. 5. As can be seen from Fig. 5, with the rolling element localized defect size increases, the acceleration of the system have a remarkable influence in $x$ and $y$ directions. Compared with the non-defective rolling bearing dynamic response, when the rolling element defects from 0.2 mm to 0.6 mm, the maximal peak value of rolling element acceleration increases in $x$ direction from 54.77 mm/s²to 1682 m/s², and the maximal peak value of rolling element acceleration increases in y direction from 52.57 mm/s²to 2777 m/s². The simulation results show that whether in the $x$ direction or $y$ direction, the acceleration of the system increases with the increase of the localized defect. In addition, compared with the outer ring of the rolling bearing defects, the rolling element has a greater influence than the outer ring under the same localized defect size.

Fig. 2Dynamic responses of rolling bearing without defect

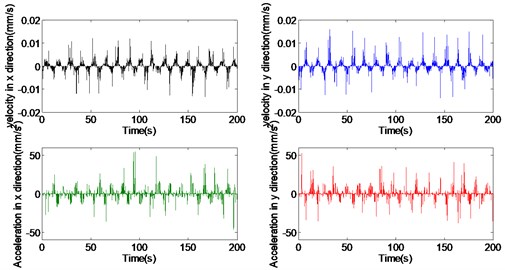
Fig. 3Comparison of velocity with different outer ring defect

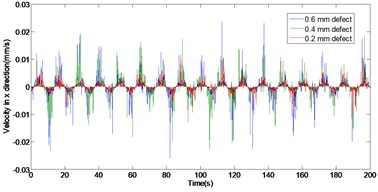
a) In $x$ direction

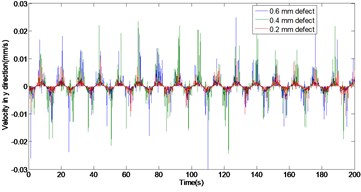
b) In $y$ direction

Fig. 4Comparison of acceleration in x and y direction with different outer ring defect

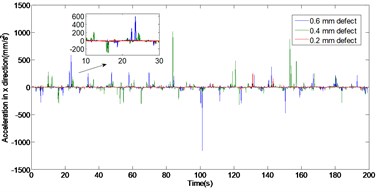
a) In $x$ direction

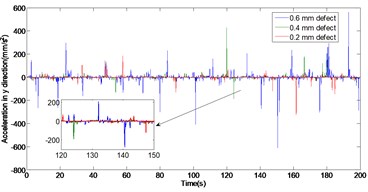
b) In $y$ direction

4. Conclusions

In this work, the nonlinear dynamics of rolling bearing with the localized defect of outer ring and rolling element are investigated. Dynamics differential equations are established based on the Lagrangian approach.

The localized defects of 0.2 mm, 0.4 mm and 0.6 mm are set on the surface of the outer ring. The dynamic simulation of these localized defects is completed by ADAMS software. The simulation results show that the amplitude of the rolling bearing is more obvious as the localized defect sizes increase. Moreover, in the same defect size, the vibration of the rolling element is more intense than the outer ring.

Fig. 5Comparison of acceleration in x and y direction with different rolling element defect

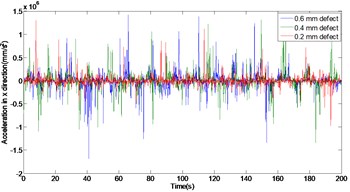
a) In $x$ direction

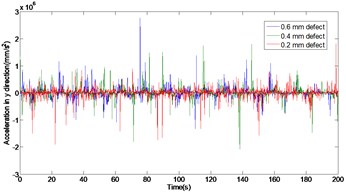
b) In $y$ direction

References

Tandon N., Choudhury A. A review of vibration and acoustic measurement methods for the detection of defects in rolling element bearings. Tribology International, Vol. 32, Issue 8, 1999, p. 469-480.

Publisher
Rafsanjani A., Abbasion S., Farshidianfar A., Moeenfard H. Nonlinear dynamic modeling of surface defects in rolling element bearing systems. Journal of Sound and Vibration, Vol. 319, Issue 3, 2009, p. 1150-1174.

Publisher
Ma H., Li H., Niu H., Song R., Wen B. Nonlinear dynamic analysis of a rotor-bearing-seal system under two loading conditions. Journal of Sound and Vibration, Vol. 332, Issue 23, 2013, p. 6128-6154.

Publisher
Liu J., Shao Y. Dynamic mode ling for rigid rotor bearing systems with a localize defect considering additional deformations at the sharp edges. Journal of Sound and Vibration, Vol. 398, 2017, p. 84-102.

Publisher
Jiang H., Wang F., Shao H., Zhang H. Rolling bearing fault identification using multilayer deep learning convolutional neural network. Journal of Vibroengineering, Vol. 19, Issue 1, 2017, p. 138-149.

Publisher
Ding F., Li X., Qu J. Fault diagnosis of rolling bearing based on improved CEEMDAN and distance evaluation technique. Journal of Vibroengineering, Vol. 19, Issue 1, 2017, p. 260-275.

Publisher
He X., Wang Q., Liu Y., Xu H., Liu S. The experimental investigation of nonlinear impact behaviors of partial rolling bearing with failure collision. Journal of Vibroengineering, Vol. 19, Issue 4, 2017, p. 2598-2610.

Publisher
Cao H., Niu L., He Z., Li Y. Dynamic modeling and vibration response simulation for high speed rolling ball bearings with localized surface defects in raceways. Journal of Manufacturing Science and Engineering-Transactions, Vol. 136, Issue 4, 2014, p. 152-161.

Publisher
Liu J., Shao Y., Tc L. Impulse vibration transmissibility characteristics in the presence of localized surface defects in deep groove ball bearing systems. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, Vol. 228, Issue 1, 2014, p. 62-81.

Publisher
Sopanen J., Mikkola A. Dynamic model of a deep-groove ball bearing including localized and distributed defects. Part 1: Theory. Proceedings of the Institution of Mechanical Engineers, Part K: Journal of Multi-body Dynamics, Vol. 217, Issue 3, 2003, p. 201-211.

Publisher
Kıral Z., Karagülle H. Vibration analysis of rolling element bearings with various defects under the action of an unbalanced force. Mechanical Systems and Signal Processing, Vol. 20, Issue 8, 2006, p. 1967-1991.

Publisher
Patil M. S., Mathew J., Rajendrakumar P. K., Desai S. A theoretical model to predict the effect of localized defect on vibrations associated with ball bearing. International Journal of Mechanical Sciences, Vol. 52, Issue 9, 2010, p. 1193-1201.

Publisher

Cited by

Joint time-frequency distribution of rolling bearings with multiple faults on outer raceway based on asymptotic model

Yunlong Li | Zhinong Li | Junyong Tao | Danyang Tian | Deqiang He

(2023)

About this article

Received

30 July 2017

Accepted

14 September 2017

Published

21 October 2017

SUBJECTS

Fault diagnosis based on vibration signal analysis

DOI

https://doi.org/10.21595/vp.2017.18914

Keywords

rolling bearing

dynamics

localized defects

outer ring

rolling element

Acknowledgements

This paper was supported by the following research Projects: “Fujian Natural Science Foundation” (Grant No. 2015J01643), “Ningde City Science and Technology Project” (Grant No. 20150034), “Education Science Project of Young and Middle-aged Teachers of Colleges and Universities in Fujian Province” (Grant No. JZ160396 and Grant No. JAT160527).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 02 29

Dynamic modeling and analysis of rolling bearing faults under time-varying excitations considering defect deformation

Chao Zhang, Yangbiao Wu, Shuai Xu, Feifan Qin, Le Wu, Bing Ouyang

Research article

2023 12 31

Diagnosis of localized defects in floating bush bearings through time-frequency domain analysis

Hiralal Patil, Dilip Patel

Research article

2022 12 06

Dynamic response and contact characteristics of shaft-bearing-pedestal system with localized defect using 2-D explicit dynamics finite element model

Huilong Li, Changfeng Yan, Junbao Yang, Jiadong Meng, Lixiao Wu

Research article

2018 05 15

Rolling element bearings localized fault diagnosis using signal differencing and median filtration

Nader Sawalhi

M. Song, S. Xiao, L. Huang, and W. Li, “Dynamic analysis of localized defects in rolling bearing systems,” Vibroengineering PROCEDIA, Vol. 14, pp. 34–39, Oct. 2017, https://doi.org/10.21595/vp.2017.18914

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2017.18914
UR  - https://doi.org/10.21595/vp.2017.18914
TI  - Dynamic analysis of localized defects in rolling bearing systems
T2  - Vibroengineering PROCEDIA
AU  - Xiao, Shungen
AU  - Song, Mengmeng
AU  - Huang, Lixia
AU  - Li, Wanxiang
PY  - 2017
DA  - 2017/10/21
PB  - JVE International Ltd.
SP  - 34-39
VL  - 14
SN  - 2345-0533
ER  - 

Copy Ris

Copied to clipboard!

@article{Xiao_2017,
	doi = {10.21595/vp.2017.18914},
	url = {https://doi.org/10.21595/vp.2017.18914},
	year = 2017,
	month = {oct},
	publisher = {{JVE} International Ltd.},
	volume = {14},
	pages = {34--39},
	author = {Shungen Xiao and Mengmeng Song and Lixia Huang and Wanxiang Li},
	title = {Dynamic analysis of localized defects in rolling bearing systems},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]S. Xiao, M. Song, L. Huang, and W. Li, “Dynamic analysis of localized defects in rolling bearing systems,” Vibroengineering PROCEDIA, vol. 14, pp. 34–39, Oct. 2017, doi: 10.21595/vp.2017.18914.

Copy IEEE

Copied to clipboard!

Xiao, Shungen, Mengmeng Song, Lixia Huang, and Wanxiang Li. “Dynamic Analysis of Localized Defects in Rolling Bearing Systems.” Vibroengineering PROCEDIA 14 (October 21, 2017): 34–39. https://doi.org/10.21595/vp.2017.18914.

Copy Chicago

Copied to clipboard!

Dynamic analysis of localized defects in rolling bearing systems

Abstract

1. Introduction

2. System model of surface defects in rolling bearing

3. Dynamic responses results and discuss

4. Conclusions

References

Cited by

About this article

Related Articles