Study on rail fastener failure testing based on fractal theory

2.1. Single fractal calculation

According to the fractal theory [8], the measurement of the multi-fractal body is:

In the formula, $E$ is the European space dimension, and when it is 1, 2, 3 respectively, the formula corresponds to the fractal curve, the fractal area or the fractal volume. $G_0$ is the corresponding $G\left(\delta \right)$ value for $D=E$. Where $E=$1, $G\left(\delta \right)$ corresponds to the length, which is obtained by the actual measurement, and the fractal relationship is as show:

where $L_0$ is the length of the smooth curve when $D=$1, and $D$ is the true fractal dimension of vibration signal, namely $D\in$[1, 2). Take the logarithm of both sides of the equation and get the following formula:

where $\mathrm{l}\mathrm{n}\delta$ and $\mathrm{l}\mathrm{n}\left(L\right(\delta \left)\right)$ are plotted on the $X$-axis and $Y$-axis respectively, and the slope is calculated by the linear fitting, and then the fractal dimension $D$ is obtained.

2.2. Multi-fractal spectrum calculation

The simple fractal dimension is a kind of integral representation of the objects studied, and the multi-fractal analysis can be considered to reflect the finer information [9].

Calculate the multi-fractal, the first thing to be obtained is the probability distribution of the investigated physical quantity on the corresponding fractal structure. If a multi-fractal set is covered with a grid of scale $\delta$, the probability distribution on the $i$th is defined as $P_i\left(\delta \right)$, then the probability that the $i$th grid with singularity ${\alpha }_i$can be defined as flows:

Let $N\left(\alpha \right)$ be the number of meshes with the singularity existence interval $\alpha$ to $\alpha +d\alpha$, $f\left(\alpha \right)$ is defined as the Hausdorff dimension of the set of grids with singularity $\alpha$, then:

The generalized dimension $D\left(q\right)$ with $q$ – order measuring moment is introduced, then:

$\alpha -f\left(\alpha \right)$ or $q-D\left(q\right)$ as two sets of independent parameters can describe the internal structure of multiple fractal, the relationship between them is as flows:

Combined with pulse residual vibration detection technique, the multi-fractal analysis of the rail vibration signal was carried out. The first step was to calculate $L_i\left(\delta \right)$ and $L\left(\delta \right)$, and then the projection coverage probability $P_i\left(\delta \right)$ was obtained. For each given $q$ value, the corresponding $\alpha \left(q\right)$ and $f\left(\alpha \left(q\right)\right)$ could be calculated according to Eqs. (4)-(6). Therefore, the multi-fractal spectrum curve $f\left(\alpha \right)~\alpha$ and the generalized fractal dimension curve with weight factor $D\left(q\right)~q$ were given.

3.1. Rail fastener failure testing with pulse stimulation and synchronized detection method

Pulse Stimulation method or hammering method was one of the most basic analytical methods in the study of the inherent mechanical properties or structural characteristics of the structural mechanics. The structure could obtain mechanical properties such as frequency, vibration mode and damping by analyzing the residual vibration response after a hit. In the case of steel rails, the residual vibration was rich in the mechanical properties of the rails, which included the constraint, that was, the degree of tightness of the fastener.

The specific detection method is: through the continuous strike and sampling along the rail, from the specific frequency band section of the three-dimensional spectrum can identify the relative position of each fastener and the loose fastener, reference to the GPS data to determine the spatial location of loose fasteners. Among them, the characteristic frequency is according to the rail model, fastener type, fastener spacing, ambient temperature and other parameters.

3.2. The track fastener inspection vehicle

Based on the previous work, the track fastener inspection vehicle was developed, which was designed to be modular and easy to disassemble and assemble. As shown in Fig. 1, the vehicle body uses a double-layer structure, the upper body includes a signal detection device, and the lower body includes a drive and a pulse signal excitation device. When testing, the lower body drives the upper body. A flexible connection between the two layers reduces the effect of body vibration on signal acquisition.

Fig. 1The track fastener inspection vehicle

4.1. Analysis based on single fractal

The fractal characteristics of rail vibration signal under periodic pulse excitation were analyzed Fig. 3 shows the fractal dimension of fastening fasteners and unfastening fasteners, respectively. It can be seen from Fig. 3 that the fractal dimension of the vibration signal is between 1 and 2, and the true fractal dimension of the vibration signal of the rail is directly measured, which provides a new way for the fractal analysis of the vibration signal. At the same time, it should be seen that the fractal dimension of the rail vibration signal has different fractal dimension in different measurement intervals ($D_l$ and $D_r$), which reflects the local characteristics of surface self-similarity, that is, multi-fractal features. The different fractal dimensions in the two scale ranges indicate that the structural features and signal complexity obtained from these two scale ranges are different. $D_l$ characterizes the structural details of the relative detail that can be obtained in the smaller scale range, and $D_r$ characterizes the relative macroscopic structural information that can be obtained in the larger scale range.

Fig. 2Estimation of fractal dimension of rail vibration signal: a), b) fastening; c), d) unfastening

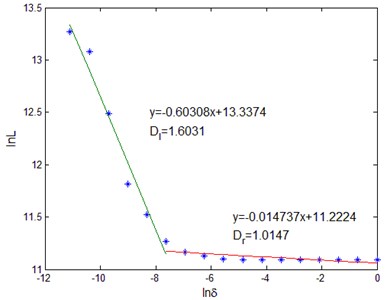
a)

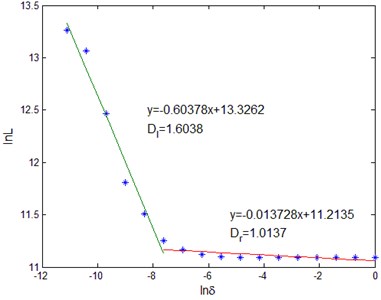
b)

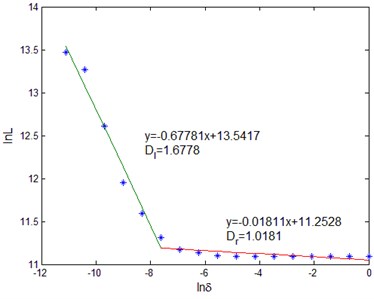
c)

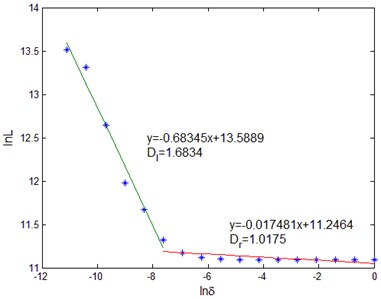
d)

It can be seen from Fig. 2 that although $D_l$ and $D_r$ characterize the different scale range of fastener release degree, but with the unfastening of the fastener, the two are both increasing. The $D_l$ of fastening fastener is located around 1.60, while the $D_l$ of unfastening fastener is located at 1.68 or so, showing an upward trend. The $D_r$ of fastening fastener is located around 1.014, while the $D_r$ of unfastening fastener is located at 1.018 or so, which is on the upward trend, but it is not obvious compared with the $D_l$ change.

4.2. Analysis based on multi-fractal

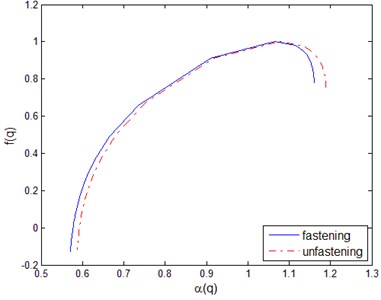
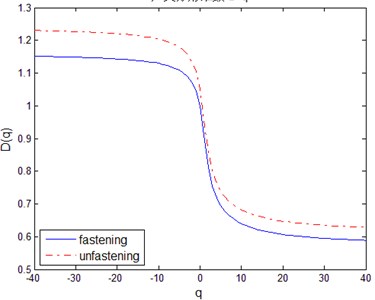
Fig. 3 shows the comparison of the multi-fractal spectrum curve $f\left(\alpha \right)~\alpha$ and $D\left(q\right)~q$ of the rail residual signal in the case of fastening and loosening. Table 1 lists the parameters of these multi-fractal spectrum, including the coordinates $({\alpha }_{min},f({\alpha }_{min}\left)\right)\text{,}$$({\alpha }_{max},f({\alpha }_{max})\text{,}$$({\alpha }_{fmax},f_{max})$, $∆\alpha$$\mathrm{\Delta }f$ and $\mathrm{\Delta }D$.

Fig. 3Multi-fractal characteristics of rail vibration signal: a) f~α, b) D~q

a)

b)

$f\left(\alpha \right)$ reflects the irregularity, non-uniformity and complexity of the subset of sub-regions with the same singularity exponent α whose magnitude depends on the number of sub-regions that make up the subset, and reveals the status and trend of micro-scale types with the same singular exponent $\alpha$ in the vibration model. As is show in Fig. 4, the curves $f\left(\alpha \right)~\alpha$ are in the right hook shape, indicating that the vibration signal is subjected to different degree of local superposition, which leads to the non-uniformity of the vibration signal distribution. With the unfastening of the fastener, $∆\alpha$ increases, indicating the maximum and minimum probability of the difference gradually increases, that is, the singularity of the length of each microelement in the vibration signal increases, which means that the vibration signal of loose fastener is more rough and irregular, and contains more details than the fastening fastener.

Curve $D\left(q\right)~q$ reflects the unevenness of the fluctuation of the vibration signal. When $q\gg$1, $D\left(q\right)$ represents the dimension of the violent region of the fluctuating change of the vibration signal. When $q\ll$ 1, $D\left(q\right)$ represents the dimension of the subsets of the more flat area of the vibration fluctuation. So that the signal fluctuation in the region can be decomposed by the severity of the change, so as to more accurately grasp the regional range of signal changes. It can be seen from Fig. 4, the range $∆D$ is with increased the release of the fastener, indicating that the difference in vibration changes gradually increased, the degree of ups and downs gradually increased.

In summary, it can be seen that some multi-fractal spectral parameters are in-phase with the fastening degree of the fastener, and these multi-fractal spectral parameters can be used to quantitatively describe the characteristics of fastener.