A two-step approach for damage detection in beam based on influence line and bird mating optimizer

1. Introduction

It is well-known that structures are suffering from all kinds of damage problems, thus a reliable structural damage identification method is needed.

Vibration based damage identification basically comprised of methods using data from frequency domain and time domain. In the last few decades, many damage identification methods have been developed using the vibration data in frequency domain [1-4]. Moreover, with the advantage of massive vibration data, methods in time domain [5-8] emerged serve as a more reliable but complicated aspect in damage identification.

In mathematical aspect, damage identification problem can be regarded as an optimization problem that aims to find the optimal solution of an objective. And with the fast development of computation, more attention was paid in algorithm these years. Neural network was among the first to be adopted to identified damage [9, 10], and therefore others heuristic algorithm such as genetic algorithm (GA) [11], particle swarm optimization (PSO) [12] and artificial bee colony (ABC) [13] are proved to the available in damage identification.

A new heuristic algorithm named Bird Mating Optimizer (BMO) was proposed by Askarzadeh [14, 15] recently, which imitates the mating behavior of birds. The algorithm was simulated and compared with GA, PSO and GSO [14] and had better accuracy.

In this paper, a two-step method for damage identification is proposed, damage is quantified as both stiffness and mass reduction in different levels. The disadvantage of heuristic algorithm is the probability of local optimum, especially with large amount of identified parameters existed. Here the displacement influence line will be utilized to determine the damage location so as to reduce the number of parameters. Then, the damage is quantified in the second step using bird mating optimizer. An objective function is established by minimizing the discrepancies between the simulated ‘measured’ dynamic acceleration responses and calculated ones. A simulation of simply supported beam is studied to show the promising results of the method.

2. Damage identification methodology

2.2. Localization of the damage by influence line residue

The localization of damage is totally based on the static displacement of the beam when a external force exerted on it. In a beam structure with length $l$, if loaded with force $P$, the static deflection $f\left(x_s\right)$ of point $x_s$ can be obtained by Eq. (3):

3

$f\left(x_s\right)={\int }_0^l\frac{M_P\left(\eta \right)\overline{M}\left(x_s,\eta \right)}{EI\left(\eta \right)}d\eta ,$

where $M_P\left(\eta \right)$ is the bending moment of beam when only external force $P$ exerted on the beam, and $\overline{M}(x_s,\eta )$ is the bending moment when a unit force exerts at the measuring point $x_s$, respectively, $f$ is the deflection function of the beam.

If we assume that there is damage existing between $a$ and $b$ with stiffness damage index $\alpha$, then the residue between damaged and intact situation is:

4

$\mathrm{\Delta }f\left(x_s\right)={\int }_a^b\frac{M_p\left(\eta \right)\overline{M}\left(x_s,\eta \right)}{EI}\left(\frac{1}{\alpha }-1\right)d\eta .$

If we set the external force $P$ as a single moving load whose location is $x_p$, then the displacement influence line residue for point $x_s$ is formed:

5

$\mathrm{\Delta }f\left(x_p,x_s\right)={\int }_a^b\frac{M_p\left(x_p,\eta \right)\overline{M}\left(x_s,\eta \right)}{EI}\left(\frac{1}{\alpha }-1\right)d\eta .$

The value of $M_p(x_p,\eta )$ within $[a,b]$ will change with $x_p$ moving from $a$ to $b$. In mechanics aspect, the change is produce directly to the change of shear force. Taking the partial derivative of $M_p(x_p,x)$ with respective to $x_p$ of Eq. (5) we get Eq. (6):

6

$\mathrm{\Delta }{f}_{x_p}\left(x_p,x_s\right)={\int }_a^b\frac{F_{sp}\left(x_p,\eta \right)\overline{M}\left(x_s,\eta \right)}{EI}\left(\frac{1}{\alpha }-1\right)d\eta ,$

where $F_{sp}(x_p,\eta )$ represents the shear force of the beam caused by moving load. A sudden change of $\mathrm{\Delta }{f}_{x_p}(x_s,x_p)$ will occur within $[a,b]$, which can be explained as: when a moving force passes through a damaged area, the shear force within the area would change from positive to negative as is illustrated in Fig. 1.

Fig. 1The change of shear force Δfxp(xs,xp)

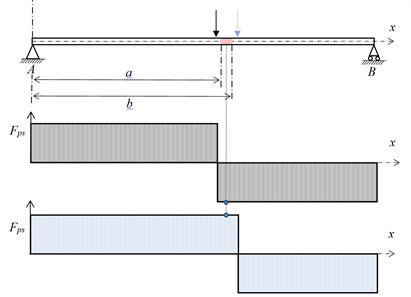
For a structure with multiple damages, the values of $\mathrm{\Delta }{f}_{x_p}(x_s,x_p)$ will be the linear sum of derivative of influence line residue (DILR) of every damage individual. For discretized model with $n$ elements and elemental length is $l/n$, the discrete influence line residue is:

7

$DILR\left(x_p\right)=\mathrm{\Delta }{f}_{x_p}\left(x_p,x_s\right)=\sum _{i=1}^{ND}\frac{F_{sp}\left(x_p,i\right)\overline{M}\left(x_s,i\right)l}{nEI}\left(\frac{1}{{\alpha }_i}-1\right),$

where $ND$ is the number of damages. One can further specify the change of DILR by taking the derivative of DILR(DDILR) to $x_p$ again. In the discretized model, the second-order central difference quotient is used to calculate the DDILR as shown in Eq. (8), where the damage parts will present as non-zero DDILR values:

8

$DDILR\left(n_i\right)=\frac{DILR\left(n_i\right)-DILR\left(n_{i-1}\right)}{leng}=\frac{\mathrm{\Delta }f\left(n_{i+1}\right)-2\mathrm{\Delta }f\left(n_i\right)+\mathrm{\Delta }f\left(n_{i-1}\right)}{len{g}^2}.$

Note that in numerical study, a damage is assumed as an elemental damage that associates with two nodes, on the other hand $\mathrm{\Delta }{f}_{x_p}$ is nodal value, so a single damage will be presented as two consecutive changes of corresponding nodes on the curve.

3. Numerical simulation

The identification procedure is shown in. A simply supported beam made of aluminum is the numerical example of the study, with length $l=$10 m and cross-sectional width $b=$0.6 m and height $h=$0.4 m, the beam is discretized into 12 Euler-Bernoulli elements, Young’s modulus is $E=$6.9 GPa and mass density $\rho =$2700 kg/m³. There are three designed damages, elements 3, 8 and 9 with Young’s modulus reduction by 10 %, 20 % and 15 %, mass reduction by 5 %, 10 % and 5 % respectively. The damping model is Rayleigh damping and the two Rayleigh coefficients are both assumed to be 0.01.

To maintain practicality, 3 % random noise presented by Eq. (15) is added to the displacement values during localization:

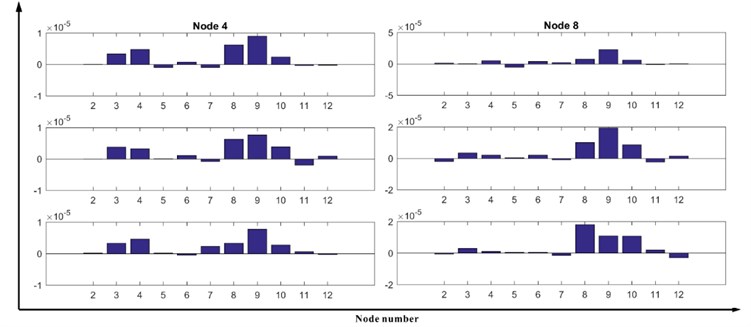
where $\mu$ is the noise level, two sensors are set in nodes 4 and 8, and the localization is processed three times to reduce the affection of noise. The DDILR are shown in Fig. 2, nodes 3, 4, 8, 9, 10 show stable changes in the chart of sensor set in node 4, and nodes 8, 9 and 10 have constant trend in the chart of the other sensor in node 8. Thus, the corresponding elements 3, 8 and 9 are selected as suspected elements.

Fig. 2DDILR of the simply supported beam

For acceleration responses $\mathbf{a}$, a Gaussian distributed random noise ${\mathbf{N}}_{oise}$ with zero mean and unit standard deviation is added as Eq. (16), where $std(\cdot )$ stands for the standard deviation of the acceleration responses in time history. The weighting factors $w_{\varphi }$ of the accMAC are all set as one:

The acceleration responses of the structure of a constant sinusoidal force acting at node 7 in the global $z$ direction with $P\left(t\right)=10^3\mathrm{s}\mathrm{i}\mathrm{n}\left(10\pi t\right)N$ is calculated by Newmark-beta method, the time increment is 0.01 second and the time duration for the response calculation is 6.0 seconds and 600 time steps in total. The arrangement of acceleration measurements are two nodes locating at nodes 5, 8.

The identified results of noise level 5 % and 10 % are shown in Fig. 3, with comparison to the result of noise free in condition. In noise free condition the identification yielded good results with maximum relative error 0.9667 % by elemental stiffness of the 3rd element, in low noise level the result is still satisfactory with maximum deviation less than 5 %, and in high noise level the maximum relative error is 5.2526 % which is not too great compared to the result of 5 %.

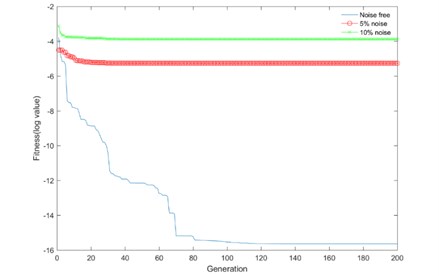
In the best logarithmic fitness values chart show in Fig. 4, it can be observed that with higher noise level, the searching process reach convergence faster but on the other hand the precision dropped.

Fig. 3Comparison of identification results under different noise levels

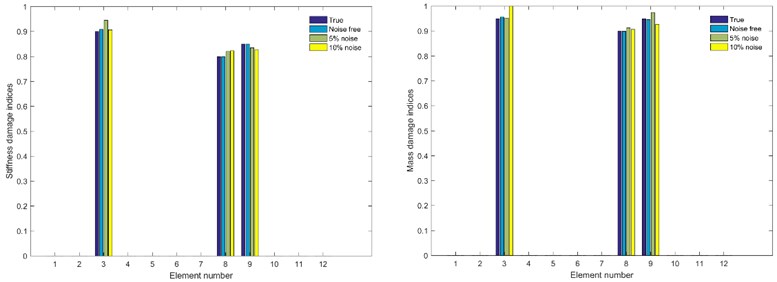
Fig. 4Comparison of logarithmic best fitness under different noise levels

4. Conclusions

By making use of the influence line residue and acceleration data, a two-step damage detection method for beam structures is proposed in this study. A damage model combined with stiffness and mass reduction is applied. The influence line data of displacement is used to reduce the dimension of the identified parameters, objective function based on acceleration and the form of MAC (Modal Assurance Criterion) is established, then BMO is used to minimizing the discrepancies between the simulated measured data and the data from damaged structure. A simply supported beam numerical simulation reflect the effectiveness of the proposed method, results under three different noise levels demonstrated that the proposed method is insensitive to measurement noise, which also manifested the robustness of the method.