Abstract
This paper presents a damage detection technique which uses change in Frequency Response Function (FRF) and Modal Strain Energy (MSE) for damage detection in beam and truss like structures. It’s a robust approach for Structural Health Monitoring (SHM) using natural frequency for structural damage assessment. This technique couples FRF with Iterative Modal Strain Energy (IMSE) method to accurately localize and quantify the damage with only few frequencies, overcoming the limitation of mode shape based damage detection methods which requires mode shapes at full coordinates but damage is either over/underestimated. In the current approach, a damage detection algorithm is developed and validated by conducting numerical studies for a Fixed-Fixed beam, both noise-free and noise-effected cases are simulated. The numerical studies reveal that proposed algorithm is capable of identifying, localizing and quantifying the damage accurately at reduce computational cost.
1. Introduction
SHM finds its application in mechanical, civil and aerospace Engineering. Damage in any structure is result of deterioration, degradation or any natural disaster in a structure during its service life. Visual inspection methods for damage assessment are dependent on instrumentation and have limited capability to determine the damage extent and severity. Vibration based Damage Identification (VBDIT) techniques have significant importance in SHM problems [1-4]. Many structural damage detection techniques are proposed in the recent decades which use the measured mode shapes and natural frequencies in the damaged structure to localize and estimate the damage. Stubbs et al. first proposed Damage Index (DI) method which uses MSE for structural damage detection [5]. Modal Strain Energy Decomposition (MSED) method is an improved form of DI method to improve the localization ability of SDI method [6, 7]. Shi et al. introduced Modal Strain Energy Change (MSEC) method using sensitivity of Modal Strain Energy Change Ratio (MSECR) to apply and validate this approach on a real life 2D structure in laboratory [8, 9]. DI & MSEC methods require paired modes of intact and damaged structures, as correct modal identification is practically difficult in some cases. Considering this limitation, Cross Modal Strain Energy (CMSE) method is developed by hu et al. to quantify the damage accurately [10]. Hwang et al. used few measured FRF for damage identification in a cantilever beam [11]. Zenzen et al. coupled FRF with BAT algorithm, minimizing the objective function based on intact and damaged structure natural frequency [12]. Khatir et al. proposed a damage detection technique using change in natural frequency and Modal Scale Factor (MSF) to minimize an objective function through PSO and BAT algorithm [13]. Pan and Zhang et al. Formulated a Noise Response Rate (NRR) in an inverse problem to select the specific mode shape for damage detection based on mode shape sensitivity to noise. This method improves the accuracy for prediction of size and location of damage [14]. An Improved modal strain energy method is formulated and validated on same Fixed-Fixed beam with noise up to 5 % provides better convergence rate than MSEC method. It was recommended to extend this study to 3D complex structures [15]. Wange et al. proposed IMSE method and validated on a cantilever beam using experimentally measured frequencies [16]. In this research work a damage detection algorithm is proposed, coupling FRF with IMSE method for structural damage detection in a Fixed-Fixed beam.
2. Methodology
2.1. Frequency response function (FRF)
Vibration based damage identification techniques (VBDIT) use change in natural frequency and mode shaps for damage detection in structure. Basic dynamic response equation for n DOF system can be expressed as Eq. (1):
For an external force and displacement and , a damped free condition FRF is expressed as:
The analytical and measured FRFs is presented as [ and [, where:
It is assumed that mass of structure remains constant and stiffness changes:
When multiplied by , Eq. (4) gives:
Based of analytical and measured FRF, beta () will be calculated as:
2.2. Iterative modal strain energy (IMSE) method
Damage severity will be estimated for damage location identified form FRF, since and Global stiffness matrix will be written as linear combination of local stiffness matrix for each element:
where is the total number of damaged elements while and show the damage severity coefficient and the damaged element. Damage severity equation will be as follows:
Structural MSE and elemental MSE changes due to damage which is applied here as an input for estimation of damage extent:
Here , , and represent the mode shapes and natural frequencies for intact and damaged structure. Using the equation Eqs. (9, 10), Eq. (8) can be written as follow:
For Eq. (11) can be simplified as:
where , and present elemental MSE, damage severity coefficient and change in natural frequency. For , Least square solution method will be used to calculate Damage severity coefficient:
Eq. (14) requires mode shapes for damaged structure at full coordinates which is difficult to obtain, here initially zero damage is assumed for Fixed-Fixed beam and IMSE method is applied to quantify the damage using measured natural frequencies:
Eqs. (14, 15) will be used for each Iteration of IMSE Method. IMSE method consists of four steps for damage quantification.
Step 1: Initialize the solution with 0, calculate where .
Step 2: Solve for using , first iteration for IMSE completes here.
Step 3: Compute from , and estimate using , where 2, 3….
Step 4: if damage severity is estimated, otherwise move to step 3, where 0.0001.
2.3. Damage detection algorithm
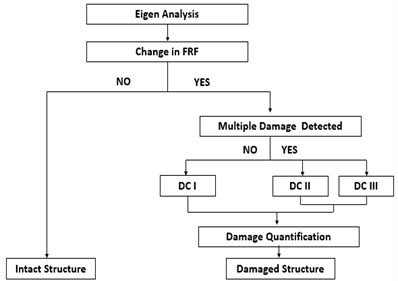
A damage detection algorithm is proposed based on FRF & IMSE method is shown in Fig. 1.
Fig. 1Damage detection algorithm based on natural frequencies
2.4. Noise-effect
In actual measured modal parameters differ by simulated FE parameters due to noise. In order to simulate this effect on dynamic response of structure, here and are stiffnesses with and without Gussian Noise for damaged elements localized. Here present the random number with standard deviation of 1 and of mean 0, shows the percentage of noise:
3. Numerical simulations
A Fixed-Fixed Beam of length 2 m with elastic modulus of 210e09 N/m2, area of 0.0014 m2 and density of 7850 Kg/m3 is considered for eigen analysis consisting of 12 Euler Bernoulli beam elements and 13 nodes with 2 DOF per node is shown in Fig. 2. Three Damage cases are simulated and first three natural frequencies are shown in Table 1.
Fig. 2FE model of a fixed-fixed beam

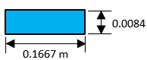
Table 1First three natural frequencies (Hz) for beam
Structure | Damage location pe (element) | Damage severity (percentage) | Natural frequency (Hz) | ||
1st | 2nd | 3rd | |||
Intact | No | Nil | 37.22 | 102.60 | 201.21 |
DCI | 6th | 35 % | 36.16 | 102.07 | 195.10 |
DCII | 3rd and 8th | 25 % and 30 % | 36.74 | 99.66 | 195.69 |
DCIII | 3rd ,6th and 9th | 40 % each | 36.67 | 93.40 | 187.54 |
4. Results and discussions
4.1. Damage localization using FRF
FRF for each damage case indicates presence of damage in the structure. Damage localization indicator uses Eq. (6) for damage location at element and its corresponding DOF.
Fig. 3Damage indicator (β) for DCI: a) based on element, b) based on DOF
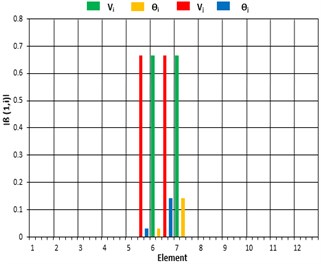
a)
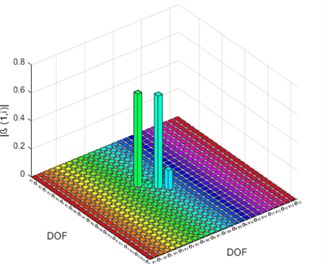
b)
4.2. Damage quantification using IMSE method
IMSE method utilizes the natural frequencies of Intact and damaged structures. For a multiple damage case it requires only first three natural frequencies for damage quantification.
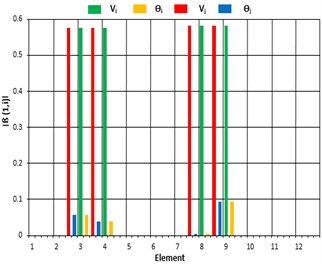
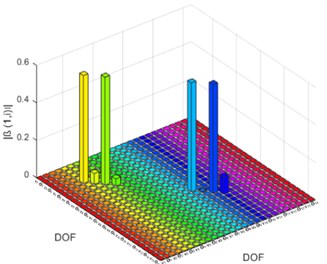
Fig. 4Damage indicator (β) for DCII: a) based on element, b) based on DOF
a)
b)
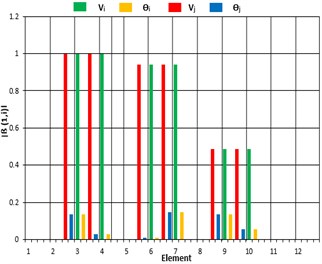
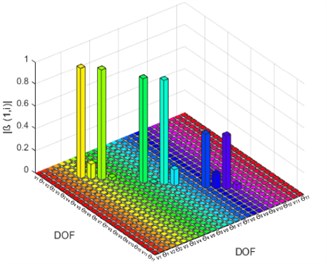
Fig. 5Damage indicator (β) for DCIII: a) based on element, b) based on DO
a)
b)
For beam structure single and multiple damage cases FRFs indicate the presence of damage in all three damage cases. For DCI, indicator shows a higher value at 6th element and its corresponding DOFs. Similarly, for DC II and DC III, there exists a higher value of at 3rd, 6th, 8th and 9th Element. This damage localization is used as an input for damage quantification in the damaged elements. For DCI, IMSE Method uses only first natural frequency of damaged structure. The damage severity estimator is estimated within 10 iterations with a tolerance of 0.0001, similarly DCII and DCIII require first two and three natural frequencies to estimate the damage severity within 9 and 11 iterations.
Fig. 6Damage severity estimator (α) for DCI, DCII and DCIII
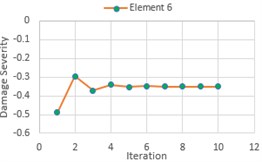
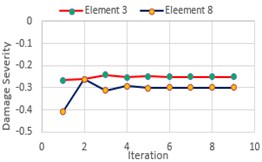
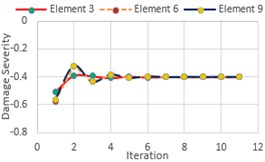
5. Conclusions
A damage detection algorithm is proposed which uses FRF as Damage indicator and uses its characteristics for damage localization. Damage severity is estimated by IMSE method which requires minimum input in form of few measured frequencies from damaged structure. The proposed approach is better than conventional mode shape based methods using only natural frequency of damaged structure as an input for damage detection. It requires only one sensor in impact hammer based modal testing setup, proving to be a cost effective approach with reduced computational cost and higher convergence rate. This method may be tested on a real structure in laboratory using actually measured natural frequencies.
References
-
Montalvão D., Maia N. M. M., Ribeiro A. M. R. A review of vibration-based structural health monitoring with special emphasis on composite materials. The Shock and Vibration Digest, Vol. 38, 2006, p. 295-324.
-
Yan Y. J., Cheng L., Wu Z. Y., et al. Development in vibration-based structural damage detection technique. Mechanical Systems and Signal Processing, Vol. 21, 2007, p. 2198-2211.
-
Fan W., Qiao P. Z. Vibration-based damage identification methods: a review and comparative study. Structural Health Monitoring, Vol. 10, 2011, p. 83-111.
-
Seo J., Hu J. W., Lee J. Summary review of structural health monitoring applications for highway bridges. Journal of Performance of Constructed Facilities, Vol. 30, Issue 4, 2016, https://doi.org/10.1061/(ASCE)CF.1943-5509.0000824.
-
Stubbs N., Kim J., Topole K. An efficient and robust algorithm for damage localization in offshore platforms. Proceedings of the ASCE Structures Congress, 1992.
-
Yang H. Z., Li H. J., Wang S. Q. Damage localization of offshore platforms under ambient excitation. China Ocean Engineering, Vol. 17, 2003, p. 495-504.
-
Li H. J., Yang H. Z., Hu S. J. Modal strain energy decomposition method for damage localization in 3D frame structures. Journal of Engineering Mechanics, Vol. 132, 2006, p. 941-951.
-
Shi Z. Y., Law S. S. Structural damage localization from modal strain energy change. Journal of Sound and Vibration, Vol. 218, 1998, p. 825-844.
-
Shi Z. Y., Law S. S., Zhang L. M. Structural damage detection from modal strain energy change. Journal of Engineering Mechanics, Vol. 126, 2000, p. 1216-1223.
-
Hu S. L. J., Li H. J., Wang S. Q. Cross-model cross-mode method for model updating. Mechanical Systems and Signal Processing, Vol. 21, 2007, p. 1690-1703.
-
Hwang H. Y., Kim C. Damage detection in structures using a few frequency response measurements. Journal of Sound and Vibration, Vol. 270, 2004, p. 1-14.
-
Roumaissa Zenzena, Idir Belaidia, Samir Khatir, Magd Abdel Wahab A damage identification technique for beam-like and truss structures based on FRF and bat algorithm. Comptes Rendus Mécanique, Vol. 346, Issue 12, 2018, p. 1253-1266.
-
Samir Khatir, Idir Belaidi, Roger Serra, Magd Abdel Wahab, Khatir Tawfiq Numerical study for single and multiple damage detection and localization in beam-like structures using BAT algorithm. Journal of Vibroengineering, Vol. 18, Issue 1, 2016, p. 202-213.
-
Pan Jingwen, Zhang Zhifang, Wu Jiurong, Ramakrishnan Karthik Ram, Singh Hemant. A novel method of vibration modes selection for improving accuracy of frequency-based damage detection. Composites Part B: Engineering, Vol. 159, 2019, p. 437-446.
-
Li Yingchao, Wang Shuqing, Zhang Min, Zheng Chunmei An improved modal strain energy method for damage detection in offshore platform structures. Journal of Marine Science and Application, Vol. 15, Issue 2, 2016, p. 182-192.
-
Shuqing Wang Iterative modal strain energy method for damage severity estimation using frequency measurements. Journal of the International Association for structural control and Monitoring, Vol. 20, Issue 2, 2013, p. 230-240.
