Damage detection in variable temperature conditions using artificial intelligence

Aman, Alexandra-Teodora; Tufisi, Cristian; Gillich, Gilbert-Rainer; Manescu, Tiberiu

doi:10.21595/vp.2023.23679

Vibroengineering Procedia

Browse Procedia

Published: 20 October 2023

Check for updates

Damage detection in variable temperature conditions using artificial intelligence

Alexandra-Teodora Aman¹

Cristian Tufisi²

Gilbert-Rainer Gillich³

Tiberiu Manescu⁴

^{1, 3, 4}Doctoral School of Engineering, Babes-Bolyai University, Cluj-Napoca 400084, Romania

^{1, 4}Department of Automation, Industrial Engineering, Textiles and Transportation, Aurel Vlaicu University, Arad, Romania

^{2, 3}Department of Engineering Science, Babes-Bolyai University, Cluj-Napoca 400084, Romania

Corresponding Author:

Cristian Tufisi

Cite the article Download PDF

Downloads 142

Abstract

When considering damage detection using the natural frequencies of structures, small frequency drops can indicate either the presence of cracks or a temperature change. This change can lead to additional stress affecting the modal parameters for specific structures, making it much harder to detect, locate, and evaluate damage accurately. The current research aims to describe a method for detecting transverse cracks in beams, considering temperature variations. The considered beam is fixed at both ends, thus inducing axial forces when the temperature is increased. The influence of temperature is considered using adjustment coefficients developed for each vibration mode. This coefficient can be used to accurately calculate the natural frequency for an intact or damaged beam. An analytical method for determining the natural frequencies caused by the changing temperature and the presence of a transverse crack is described and used to generate data for training a feedforward artificial neural network (ANN). The ANN’s capability of determining the position of transverse cracks in double-clamped beams subjected to small temperature changes is proven by creating numerical simulations with known crack positions and thermal conditions for testing the developed method.

1. Introduction

Transverse cracks in double-clamped beams can negatively affect their structural integrity, leading to unsafe consequences in various engineering applications. The development of efficient crack detection techniques is of crucial importance [1]. In recent years, researchers have explored different approaches that combine analytical methods and artificial intelligence with the consideration of environmental variations for enhanced crack detection and localization [2-4].

Traditionally, analytical methods have provided valuable insights into the behavior of double-clamped beams subjected to external factors such as cracks [5]. One widely recognized technique employs the squared normalized modal curvature as a reliable indicator of crack presence [6]. This method is based on the fact that cracks modify the modal parameters of the beam, altering its dynamic response. While this analytical approach has proven effective, further improvements are required to enhance detection accuracy and precisely locate the cracks.

To overcome these shortcomings, researchers have turned their attention to artificial intelligence techniques [7]. The concept of vibration-based damage identification comprehends comparing the natural frequencies obtained from the undamaged beam with those from the damaged beam [8]. By employing natural frequencies, even small changes caused by cracks can be detected [9]. Moreover, employing artificial intelligence models allows for more efficient analysis of the measured data, significantly enhancing crack detection accuracy.

In addition to the mentioned techniques, considering temperature variations offers a valuable contribution to the crack detection problem [10]. Temperature changes result in thermal expansion or contraction of the material, imposing additional strains and stresses on the beam [11]. As a result, in practical situations, monitoring structures requires considering both operational and environmental influences [12]. Occasionally, fluctuations in temperature can lead to more significant parameter variations compared to the impact of early-stage damage, making it challenging to differentiate between these two factors [13]. By accounting for temperature variations during the crack detection process, an enhanced understanding of the crack behavior and severity can be achieved with higher accuracy and reliability [14].

The current study presents an innovative approach to identify transverse breathing cracks in beams under different temperature conditions, utilizing their natural frequencies. The primary issue tackled is the challenge of differentiating minor frequency decreases resulting from cracks from those caused by temperature variations, by using an analytical method that can give an accurate result regarding the impact that transverse cracks have on the structural modal characteristics of beams in varying temperature conditions.

This paper continues the research presented in [15], aiming to develop an innovative approach to detect and locate transverse cracks in double-clamped steel beams with high accuracy, even when temperature changes occur. Our proposed methodology combines a well-established method [15] using artificial intelligence models and incorporating temperature adjustment coefficients into the analysis. By employing this comprehensive context, we aim to enhance crack detection sensitivity and localization precision, ensuring the safety and reliability of structural systems.

The developed ANN model accuracy is tested by performing modal simulations for double-clamped steel beams in the simulation software ANSYS, considering known damage scenarios and thermal conditions. The mathematical model

In standard applications, the detection of transverse cracks using modal parameters is approached by assuming unchanged environmental conditions. In real-life cases, the environment is often subjected to changes, which must be considered when applying global damage detection techniques.

Temperature changes affect double-clamped beams most because the constraining conditions lead to supplementary axial loads. In the current study, we employ a method developed in [15] to calculate the RFS values for damage locations by considering temperature adjustment coefficients. The specimen is a steel beam with its physical properties and dimensions presented in Table 1. The beam is clamped on both ends, and the considered damage is a transverse crack of known depth $a$ and location $x$ as presented in Fig. 1.

Fig. 1Considered damaged beam

Table 1The beam’s physical, mechanical, and geometrical parameters

Mass density $ρ$ [kg/m³]	Young modulus $E$ [N/m²]	Poisson ratio $υ$ [–]	Thermal expansion coefficient $α$ [1/°C]	Length [mm]	Width [mm]	Thickness [mm]
7850	2.1·1011	0.3	1.15·10-5	1000	50	10

If the reference temperature $T_{r e f}$ is increased with $Δ T$ , the internal load is given by [15]:

1

P (T) = α \cdot E \cdot A \cdot Δ T,

where $A$ is the cross-section of the beam.

The characteristic equation for a beam fixed at both ends is:

2

ζ \sin ζ + 2 \cos ζ - 2 = 0 .

The critical forces $P_{c r}$ and critical temperature $T_{c r}$ have several solutions and can be found as:

3

P_{c r - i} = \frac{{ζ_{i}}^{2} E \cdot I}{L^{2}},

4

T_{c r - i} = T_{r e f} + Δ T_{c r} = T_{r e f} + \frac{P_{c r - i}}{α \cdot E \cdot A} .

By applying the transcendental Eq. (5), the values for the first six bending modes are obtained:

5

1 + \cos λ \cdot \cosh λ = 0 .

In the case of compression load, the expression for the case of fixed-fixed ends, for $ζ_{i} \neq λ_{i}$ , the natural frequencies are obtained with Eq. (6):

6

f_{i} (P) = f_{r e f - i} \sqrt{1 - \frac{P}{P_{c r - i}}} .

The mathematical relation expressing the frequency considering the temperature change is obtained by substituting Eqs. (1) and (3) in Eq. (6), as:

7

f_{i} (T) = f_{r e f - i} \sqrt{1 - \frac{α A (T - T_{r e f}) L^{2}}{I ζ_{i}^{2}}} = f_{r e f - i} \cdot κ_{i} (T),

where $k_{i} (T)$ is the temperature adjustment coefficient. It is employed to find the frequency at any pre-buckling temperature if the frequency at a reference temperature and the temperature change are known.

For a reference temperature $T_{r e f}$ , the first six buckling eigenvalues $ζ_{i}$ , critical force $P_{c r}$ , and critical temperature $T_{c r}$ values for the double-clamped beam are shown in Table 2.

Table 2The first six buckling eigenvalues, critical forces, and temperatures

Buckling mode $i$	Eigenvalue $ζ_{i}$	Critical force $P_{c r - i}$ [N]	Critical temperature $T_{c r - i}$ [°C]
1	6.283185	33885.64	50.607
2	8.986818	69321.50	80.523
3	12.56637	135542.6	136.43
4	15.45050	204899.7	194.98
5	18.84956	304970.8	279.46
6	21.80824	408222.9	366.63

The mathematical equation predicting the natural frequency for a damaged beam subjected to a temperature change is found by applying Eq. (8):

8

f_{i D} (x_{D}, a, T) = f_{i} (T) \{1 - γ (a) {[{\bar{ϕ^{''}}}_{i} (x_{D})]}^{2}\} = f_{r e f - i} \cdot \sqrt{1 - \frac{α A (T - {T_{r e f}}_{- i}) L^{2}}{I ζ_{i}^{2}}} \cdot \{1 - γ (a) {[{\bar{ϕ^{''}}}_{i} (x_{D})]}^{2}\} .

The severity $γ (a)$ for a given crack depth $a$ can be found by applying the method presented in [16], and the squared normalized modal curvature for the double-clamped beam can be found using Eq. (9):

9

{ϕ^{''}}_{i} (x) = (\cos λ_{i} \frac{x}{L} + \cosh λ_{i} \frac{x}{L}) - \frac{(\sin λ_{i} + \sinh λ_{i})}{(\cos λ_{i} - \cosh λ_{i})} (\sin λ_{i} \frac{x}{L} + \sinh λ_{i} \frac{x}{L}) .

2. Training the ANN with the mathematical model

The ANN is trained to evaluate the first six weak-axis bending natural frequency data obtained from a double-clamped steel beam subjected to various temperature conditions (ranging from 22 to 50 °C) while it is also affected by a transverse breathing crack. This section details the method for generating the training data for the ANN using the proposed algorithm. The training data is obtained by calculating the natural frequencies for a double-clamped beam, starting from a reference temperature $T_{r e f} =$ 22 °C, for which Eq. 10 is used:

10

f_{i} = \frac{λ_{i}^{2}}{2 π} \sqrt{\frac{E I}{ρ A L_{}^{4}}} .

Furthermore, we consider several thermal scenarios to depict the thermal adjustment coefficients. These imply four temperature increase values, i.e., $Δ T =$ 7, 13, 18, and 28 °C. The obtained coefficients are presented in Table 3.

Table 3Obtained thermal adjustment coefficients

Temperature increase $Δ T$ [°C]	$k_{1}$ (T)	$k_{2}$ (T)	$k_{3}$ (T)	$k_{4}$ (T)	$k_{5}$ (T)	$k_{6}$ (T)
29	0.86909	0.93829	0.96893	0.97956	0.98631	0.98979
35	0.73863	0.88197	0.94148	0.96169	0.97443	0.98096
40	0.60893	0.83213	0.91799	0.94654	0.96441	0.97354
50	0.14573	0.72219	0.86908	0.91549	0.94406	0.14573

After obtaining the $k_{i} (T)$ coefficients, we calculate the frequency for each temperature for the intact beam by using Eq. (7). Next, we calculate the frequency for a damaged beam again for each selected temperature using Eq. (8). The damage is a transverse crack, that is removed with a step of 2 mm along the hall length of the beam. The crack depth is 2 mm, meaning a cross-section reduction of 20 %. The severity value $γ (a)$ has been obtained by applying the procedure described in [16]. Due to the symmetrical constraining condition, the training data is calculated for only half of the beam. Thus, two possible damage locations can be considered as the predicted position, starting from the left or right sides of the beam. It results in 1250 training scenarios.

Fig. 2ANN training performance

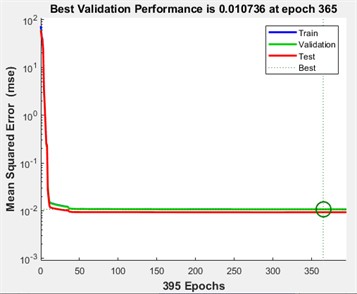
a) Performance diagram

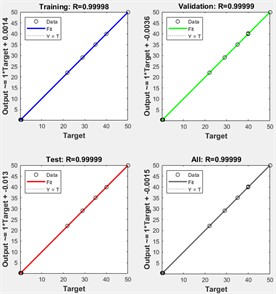
b) Regression diagrams

The ANN is a feedforward neural network with two hidden layers, each containing 50 neurons, and is developed using MATLAB software. The network is trained to predict the location of the crack and the temperature of the beam, using the trainBR function. After the training is completed, the first network evaluation is done by analyzing the performance and regression diagrams, shown in Fig. 2.

The diagrams in Fig. 2 illustrate that the trained ANN is well-equipped to handle the complexity of transverse crack localization in a varying temperature environment.

3. Testing the ANN using ANSYS simulations and thermal transient analysis

The validation of the developed ANN for transverse crack localization in a double-clamped steel beam, having its dimensions presented in Table 1, subjected to varying temperature conditions, is performed using simulated damage scenarios defined within ANSYS software.

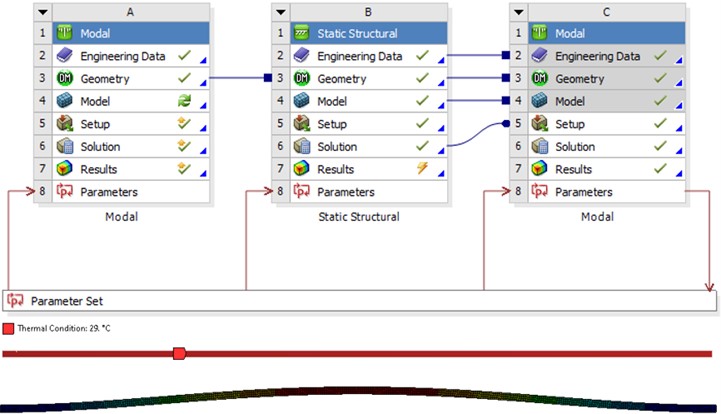
These scenarios included the introduction of a 2 mm depth transverse crack into the beam structure and encompassed a range of temperatures from 22 to 44 °C. To accurately simulate real-world conditions, the models employ the thermal transient method to integrate the effects of thermal stresses induced by axial forces resulting from temperature fluctuations starting from $T_{r e f} =$ 22 °C. Modal analysis was employed to extract the first six weak-axis eigenfrequencies of the damaged beam under different temperature conditions. The analysis setup is presented in Fig. 3.

The modal analysis results, consisting of the natural frequencies, served as the basis for feature extraction in the ANN testing process. This information was fed into the trained ANN model, allowing the network to predict the presence and location of the transverse crack for each simulation scenario.

Fig. 3Simulation setup

The results obtained for each damage scenario are presented in Table 4. From the results, one can observe that the maximum difference between the real and the predicted crack position is 42 mm, for small structures this error is negligible, but for larger structures, the method should be further improved by developing more complex ANN structures and by normalizing the data.

4. Conclusions

While the accuracy of the developed Artificial Neural Network (ANN) for transverse crack detection in a double-clamped steel beam under varying temperature conditions might not have reached optimal levels, the error being over 3 % for damage cases 6, 8, 11, 14 in the current study, the research provides a solid foundation for future advancements. Incorporating thermal stresses induced by temperature fluctuations into the ANN testing process represented a significant step toward real-world applicability. Despite the challenges, the study showcases the potential of integrating modal analysis results into ANN-based damage detection frameworks, showing that in some cases, the damage location has been predicted with an error of 1 mm.

Table 4Obtained results

Scenario No.	Damage location $x$ [m]	Temperature [°C]	Predicted location $x$ [m]	Error [%]	Predicted temperature [°C]
1	0.02	29	0.024	0.40	31.70
2	0.031	35	0.021	1.00	34.09
3	0.046	40	0.050	0.40	41.79
4	0.058	44	0.059	0.10	48.45
5	0.063	29	0.040	2.30	31.76
6	0.089	35	0.059	3.00	34.05
7	0.169	40	0.201	3.20	41.48
8	0.294	44	0.253	4.10	48.33
9	0.562	29	0.558	0.40	29.06
10	0.625	35	0.649	2.40	33.92
11	0.789	40	0.747	4.20	41.38
12	0.802	44	0.799	0.30	48.28
13	0.226	37	0.249	2.30	36.96
14	0.192	26	0.227	3.50	23.21
15	0.058	25	0.04	1.80	22.22

One promising way for future research lies in exploring the utilization of relative frequency shifts. A more sensitive and accurate detection method can be developed by examining the relative changes in eigenfrequencies due to transverse cracks. This approach could enhance the ANN's ability to discern subtle differences in the structural behavior caused by cracks, especially under varying thermal conditions.

References

M. Senthilkumar, S. Manikanta Reddy, and T. G. Sreekanth, “Dynamic study and detection of edge crack in composite laminates using vibration parameters,” Transactions of the Indian Institute of Metals, Vol. 75, No. 2, pp. 361–370, Feb. 2022, https://doi.org/10.1007/s12666-021-02419-y

Publisher
K. Khangamlung, A. K. Muhammad, and A. K. Kamran, “Characterising modal behaviour of a cantilever beam at different heating rates for isothermal conditions,” Applied Sciences, Vol. 11, p. 11104, 2021, https://doi.org/10.3390/app11104375biographies

Publisher
J. Luo, M. Huang, and Y. Lei, “Temperature effect on vibration properties and vibration-based damage identification of bridge structures: a literature review,” Buildings, Vol. 12, No. 8, p. 1209, Aug. 2022, https://doi.org/10.3390/buildings12081209

Publisher
S. Sharma and S. Sen, “Damage detection in presence of varying temperature using mode shape and a two-step neural network,” Lecture Notes in Civil Engineering, Vol. 103, pp. 285–299, 2021, https://doi.org/10.1007/978-981-15-8138-0_23

Publisher
M. Seguini, N. Djamel, B. Djilali, S. Khatir, and M. Abdel Wahab, “Crack prediction in beam-like structure using ANN based on frequency analysis,” Frattura ed Integrità Strutturale, Vol. 16, No. 59, pp. 18–34, Dec. 2021, https://doi.org/10.3221/igf-esis.59.02

Publisher
M. Dahak, N. Touat, and M. Kharoubi, “Damage detection in beam through change in measured frequency and undamaged curvature mode shape,” Inverse Problems in Science and Engineering, Vol. 27, No. 1, pp. 89–114, Jan. 2019, https://doi.org/10.1080/17415977.2018.1442834

Publisher
N. Gillich et al., “Beam damage assessment using natural frequency shift and machine learning,” Sensors, Vol. 22, No. 3, p. 1118, Feb. 2022, https://doi.org/10.3390/s22031118

Publisher
S. Loutridis, E. Douka, and L. J. Hadjileontiadis, “Forced vibration behaviour and crack detection of cracked beams using instantaneous frequency,” NDT and E International, Vol. 38, No. 5, pp. 411–419, Jul. 2005, https://doi.org/10.1016/j.ndteint.2004.11.004

Publisher
X. F. Yang, A. S. J. Swamidas, and R. Seshadri, “Crack identification in vibrating beams using the energy method,” Journal of Sound and Vibration, Vol. 244, No. 2, pp. 339–357, Jul. 2001, https://doi.org/10.1006/jsvi.2000.3498

Publisher
S. Sharma and S. Sen, “Structural damage detection in presence of temperature variability using 2D CNN integrated with EMD,” Structural Monitoring and Maintenance, Vol. 8, No. 4, pp. 379–402, Dec. 2021, https://doi.org/10.12989/smm.2021.8.4.379

Publisher
M. Azadi, “Free and forced vibration analysis of FG beam considering temperature dependency of material properties,” Journal of Mechanical Science and Technology, Vol. 25, No. 1, pp. 69–80, Jan. 2011, https://doi.org/10.1007/s12206-010-1015-y

Publisher
J. D. Hios and S. D. Fassois, “A global statistical model based approach for vibration response-only damage detection under various temperatures: A proof-of-concept study,” Mechanical Systems and Signal Processing, Vol. 49, No. 1-2, pp. 77–94, Dec. 2014, https://doi.org/10.1016/j.ymssp.2014.02.005

Publisher
A. Deraemaeker, A. Preumont, and J. Kullaa, “Modeling and removal of environmental effects for vibration based SHM using spatial filtering and factor analysis,” in Proceedings of IMAC XXIV, 2006.

Search CrossRef
J.-T. Kim, J.-H. Park, and B.-J. Lee, “Vibration-based damage monitoring in model plate-girder bridges under uncertain temperature conditions,” Engineering Structures, Vol. 29, No. 7, pp. 1354–1365, Jul. 2007, https://doi.org/10.1016/j.engstruct.2006.07.024

Publisher
G.-R. Gillich, H. Furdui, M. Abdel Wahab, and Z.-I. Korka, “A robust damage detection method based on multi-modal analysis in variable temperature conditions,” Mechanical Systems and Signal Processing, Vol. 115, pp. 361–379, Jan. 2019, https://doi.org/10.1016/j.ymssp.2018.05.037

Publisher
C. Tufisi et al., “Determining the severity of open and closed cracks using the strain energy loss and the Hill-Climbing method,” Applied Sciences, Vol. 12, No. 14, p. 7231, Jul. 2022, https://doi.org/10.3390/app12147231

Publisher

About this article

Received

02 October 2023

Accepted

16 October 2023

Published

20 October 2023

SUBJECTS

Mathematical models in engineering

DOI

https://doi.org/10.21595/vp.2023.23679

Keywords

crack localization

double-clamped beam

natural frequency

artificial intelligence

temperature variations

Acknowledgements

The authors have not disclosed any funding.

Data Availability

The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.

Conflict of interest

The authors declare that they have no conflict of interest.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous

Research article

2020 04 02

Damage detection in a fixed-fixed beam using natural frequency changes

Muhammad Wasif Khan, Naveed Akmal Din, Rizwan Ul Haq

Research article

2019 04 25

Assessing multiple cracks in beams by a method based on the damage location coefficients

Gilbert-Rainer Gillich, Alexandra Teodora Aman, Dorian Nedelcu, Codruta Oana Hamat, Tiberiu Manescu

Research article

2018 03 31

On crack detection in curved beams using change of natural frequency

Maryam Zare

Research article

2016 12 31

Detecting structural damage in Timoshenko beams based on optimization via simulation (OVS)

Reza Farokhzad, Benyamin Mohebi, Gholamreza Ghodrati Amiri, Mohsen Ghafory Ashtiany

A.-T. Aman, C. Tufisi, G.-R. Gillich, and T. Manescu, “Damage detection in variable temperature conditions using artificial intelligence,” Vibroengineering Procedia, Vol. 51, pp. 186–192, Oct. 2023, https://doi.org/10.21595/vp.2023.23679

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2023.23679
UR  - https://doi.org/10.21595/vp.2023.23679
TI  - Damage detection in variable temperature conditions using artificial intelligence
T2  - Vibroengineering Procedia
AU  - Aman, Alexandra-Teodora
AU  - Tufisi, Cristian
AU  - Gillich, Gilbert-Rainer
AU  - Manescu, Tiberiu
PY  - 2023
DA  - 2023/10/20
PB  - JVE International Ltd.
SP  - 186-192
VL  - 51
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Aman_2023,
	doi = {10.21595/vp.2023.23679},
	url = {https://doi.org/10.21595/vp.2023.23679},
	year = 2023,
	month = {oct},
	publisher = {{JVE} International Ltd.},
	volume = {51},
	pages = {186--192},
	author = {Alexandra-Teodora Aman and Cristian Tufisi and Gilbert-Rainer Gillich and Tiberiu Manescu},
	title = {Damage detection in variable temperature conditions using artificial intelligence},
	journal = {Vibroengineering Procedia}
}

Copy Bibtex

Copied to clipboard!

[1]A.-T. Aman, C. Tufisi, G.-R. Gillich, and T. Manescu, “Damage detection in variable temperature conditions using artificial intelligence,” Vibroengineering Procedia, vol. 51, pp. 186–192, Oct. 2023, doi: 10.21595/vp.2023.23679.

Copy IEEE

Copied to clipboard!

Aman, Alexandra-Teodora, Cristian Tufisi, Gilbert-Rainer Gillich, and Tiberiu Manescu. “Damage Detection in Variable Temperature Conditions Using Artificial Intelligence.” Vibroengineering Procedia 51 (October 20, 2023): 186–92. https://doi.org/10.21595/vp.2023.23679.

Copy Chicago

Copied to clipboard!

Damage detection in variable temperature conditions using artificial intelligence

Abstract

1. Introduction

2. Training the ANN with the mathematical model

3. Testing the ANN using ANSYS simulations and thermal transient analysis

4. Conclusions

References

About this article

Related Articles