Method of bearing fault diagnosis based on time-frequency manifold analysis

1. Introduction

In 2000, two papers on isometric graph (Isometric Mapping, ISOMAP) and LLE (local Linear, LLE) algorithm were published in Science Journal [1, 2]. Based on the manifolds learning algorithm, the machine learning and data mining technology was given a new impetus.Classic manifold learning methods are isometric feature mapping(Isometric Mapping, ISOMAP) [1], LLE (Locally Linear Embedding, LLE) [2], Laplace feature mapping (Laplacian eigenmaps, LE) [3], local tangent space alignment (Local Tangent Space Alignment, LTSA) [4] and the like. Wang Xiangxiang [5] use Wigner-Ville distributed fault diagnosis method combined with the LTSA, the successful solution of the problem of extracting weak fault gear; Xiang Dan[6] use EMD and Sample Entropy LLTSA combination of methods, effectively extract the weak fault feature of rolling bearings; Li Feng [7] use linear Local tangent space alignment to dimension Simplification, to identify the weak fault of gear and verified the effectiveness of the method; Yuan Deqiang [8] use LLTSA good clustering and classification performance to reduce dimensionality of the fault data, and fault diagnosis; Sun Bin [9] use LLTSA and limit learning machine combination, use time domain and frequency domain parameters to bearing fault diagnosis; Zang Huaigang [10] use of EMD and smoothed pseudo Wigner-Ville combination, fully extracted smoothed pseudo Wigner-Ville spectral entropy of signals, bearing fault diagnosis.

2. Smoothed pseudo Wigner-Ville distribution and linear local tangent space alignment

Wigner-Ville distribution is a good method of frequency analysis, it can effectively decompose the signal frequency characteristics. An existing signal, then the Wigner-Ville distributed as follows [11, 12]:

where: $x\left(t\right)$ – the actual signal $s\left(t\right)$ of the complex frequency signal, it use Hilbert transform the original signal with phase shift 90°, composed of analytical signal, which is $x\left(t\right)=s\left(t\right)+jHT\left(s\right(t\left)\right)$ [13]; $x^{*}\left(t\right)$ – conjugate signal of the actual signal $s\left(t\right)$; $x^{*}(t-\frac{1}{2}\tau )x(t+\frac{1}{2}\tau )$ – the instantaneous signal correlation function.

In order to solve the cross term problem of Wigner-Ville, a smooth pseudo Wigner-Ville distribution is proposed, two smoothing window function $h\left(\tau \right)$ and $g\left(u\right)$ are defined, the use of the smoothing window function can suppress cross-term effect of Wigner-Ville, the use of these two smoothing window function improved Wigner-Ville distribution can be defined as:

The linear local tangent space alignment algorithm (LLTSA) is a local maximum linear extension of local tangent space arrangement (LTSA), it was the idea that the local tangent space alignment (LTSA) with adaptive linear block combination, by differential Euclidean distance and geodesic distance, and with a pre-given threshold $\theta$ compare to construct local data blocks, and using geometric perturbations to strictly control the local linear characteristic of nonlinear data, the loss of the feature information of the reduced dimension is less than that of the original LTSA [15].

3. Multi-scale sub-band sample entropy

In real life, because of the complexity of vibration data, the average sample entropy cannot be extracted from the data. To solve this problem raised here multi-scale entropy concept of sub-band samples, the first signal using wavelet packet decomposition into multi-scale signal, the initial value of the signal feature extraction, because the method can further data internally, and eigenvalues. The specific steps:

(1) Signal provided by the smoothed pseudo Wigner-Ville after decomposition of $X$;

(2) The signal $X=[x_1,x_2,x_3,\cdots ,x_n{]}^T$ is decomposed by wavelet packet, which is:

where, $h_k$ is orthogonal highpass filter coefficient; $g_k$ is orthogonal to the low-pass filter coefficient; $Y_0\left(t\right)=\phi \left(t\right)$ is scaling function; $Y_1\left(t\right)=\varphi \left(t\right)$ wavelet function, From this, we can know that the function $\left\{Y_n\right(t\left)\right|n\in z^{+}\}$ is the orthogonal wavelet packet of $\phi \left(t\right)$;

(3) After the signal $j$ is decomposed and reconstructed by wavelet packet $X\left(t\right)$ layer, we can get the $2^j$ wavelet packet decomposition and reconstruction sequence $S\left(j,k\right)$$(k=\mathrm{0,1},2,\cdots ,2^j-1)$, $S(j,k)$ is the first $k$ node sequence of $X\left(t\right)$ layer decomposition of signal $j$, the wavelet packet decomposition and reconstruction can be regarded as a kind of wavelet packet, then the definition of this kind of partition is defined:

where, ${\phi }_{F(j,k)}\left(i\right)$ is the $i$-th value of ${\phi }_{F(j,k)}(i=\mathrm{1,2},3,\cdots ,N)$, $N$ is the length of the original signal, herein $j=$ 3, then $k=$ 0, 1, 2,…, 7, and ${\phi }_{F(j,k)}$ is ${\phi }_{(j,k)}$ of the Fourier transform;

(4) According to the data length $M$ of the after wavelet packet decomposition sequence of nodes $S(j,k)$, select the best maximum stencil length $D$ ($D<M$) of the sample entropy;

(5) $S(j,k)$ data in accordance with the maximum template length of data is divided $a$$(a=M/D)$ into sub-band $S_i\left(j,k\right)(i=\mathrm{1,2},\cdots ,a)$;

(6) In $S_1(j,k)$, for example, a given dimension $m$,the sub-band signals in accordance with the serial number $S_1(j,k)$ composed of a group $m$ -dimensional vector, which is:

(7) Calculating the distance between $S_1(j,k)\left(i\right)$ and $S_1(j,k)\left(n\right)$ denoted by $d_{in}$, then $d_{in}$ is:

(8) Given threshold $r$, statistic the number of $d(i,n)<r$ for each $i$, the ratio $B_i^m\left(r\right)$ of this number and the total number $D-m+1$ of distance, $B_i^m\left(r\right)=\frac{\left[d\right(i,n)<r]}{D-m+1}$, where $1<n<D-m$, $i\ne n$, find the average for all $i$, calculated as follows:

(9) To increase the dimension $m+1$, repeating steps Eqs. (6)-(8), to give $B^{m+1}\left(r\right)$;

(10) If $D$ is finite, namely $S_1(j,k)$ of the sample entropy is $c_1$, the sample entropy $c_1$ is:

(11) Repeat steps Eqs. (6)-(10), respectively to calculated sample entropy $c_1$, $c_2$, $c_3$,…, $c\left(a\right)$ of $S_1(j,k)$, $S_2(j,k)$, $S_3(j,k)$,…, $S_a(j,k)$;

(12) The feature matrix is constructed by the sample entropy $c_1$, $c_2$, $c_3$,…, $c\left(a\right)$, and the normalization process, referred to as $C(j,k)$, the node sequence of sub-band samples entropy of $C(j,k)$;

(13) Were calculated for each sequence of nodes $S\left(j,k\right)(j=3)$, then $k=$ 0, 1, 2,…, 7, remember the sample entropy is $C\left(\mathrm{3,0}\right)$, $C\left(\mathrm{3,1}\right)$, $C\left(\mathrm{3,2}\right)$, $C\left(\mathrm{3,3}\right)$, $C\left(\mathrm{3,4}\right)$, $C\left(\mathrm{3,5}\right)$, $C\left(\mathrm{3,6}\right)$ and $C\left(\mathrm{3,7}\right)$, and the feature matrix structure, a naturalization process, you can obtain the fault signal sub-band samples multi-scale entropy is $T$, then:

As can be seen from the above steps, the value of $m$ and $r$ is closely related to the sample entropy, therefore, to determine the value of $m$ and $r$ is very important. Where $m=\text{1}$ or $m=\text{2}$, $0.1S_{td}\le r\le 0.25S_{td}$ ($S_{td}$ difference is the standard of the original data), this article takes $m=\text{2}$, $r=0.2S_{td}$.

4. Fault diagnosis method based on time-frequency manifold

Because of the modal aliasing effect in the process of sub-band decomposition, a smooth pseudo-Wigner-Ville distributed modal aliasing effect is introduced, and the mining sample entropy of the signal in the frequency domain can be used to solve the problem of insufficient resolution of the pseudo-Wigner distribution in the frequency domain after smoothing, and the main characteristic frequency domain signals of the manifolds can be obtained by using the superiority of LLTSA for nonlinear feature extraction. The steps of this approach are as follows:

(1) The original signal preprocessing, get after the data preprocessing;

(2) After preprocessing of data after the Hilbert transform, get analytical signal;

(3) Select the appropriate window function and its length, it will pass the data after the Hilbert transform to decompose with a smooth pseudo Wigner-Ville distribution;

(4) Obtaining signal has been smoothed pseudo Wigner-Ville distribution sub-band multi-scale sample entropy;

(5) To obtain the multi-scale sample entropy comes with high-dimensional feature matrix constructed, and normalization;

(6) After normalization of the matrix will be LLTSA manifold learning process, mining frequency manifold structure when its main internal, and fault identification.

5. Experimental verification

In this paper, data from the American public data Case Western Reserve University’s data center bearing, bearing model 6205-2RS JEM SKF deep groove ball bearings, In order to make the data representative, Select normal, inner fault, outer ring fault and roller fault four types of data in each of the four groups, normal data fault size is 0", the fault size of the inner ring, outer ring and rolling element fault is 0.007", motor loads are 0 HP, 1 HP, 2 HP and 3 HP, the speed is 1797 rpm, 1772 rpm, 1750 rpm and 1730 rpm, the sampling frequency of the signal is 12000 Hz.

Fig. 1 is a ball of failure time-frequency diagram and spectrum. smooth pseudo Wigner-Ville distribution can be accurately extracted the instantaneous energy of the signal, Hilbert transform signal after signal into analytic signal, and then smoothed pseudo Wigner-Ville distribution of decomposition, feature extraction in order to make more accurate, where the smoothing window windowing to suppress cross-impact items, set up here two window function $h\left(\tau \right)$ and $g\left(u\right)$, select the type of two windows function is hamming window, the length of the window function, respectively $\frac{N}{10}+1$ and $\frac{N}{4}+1$ ($N$ is the length of the test signal). The following Fig. 2, 3 for the signal through a smooth pseudo Wigner-Ville distribution and Wigner-Ville distribution of the time-frequency map of the decomposition. From Fig. 2 As can be seen, Wigner-Ville distribution serious cross-term problem, it has been unable to distinguish between signals intrinsic terms and cross-term, the signals have been contaminated, and Fig. 3 Smoothing Pseudo Wigner-Ville no cross-term distribution, signal clearly visible.

Fig. 1Time domain and frequency spectrum of ball failure on bear

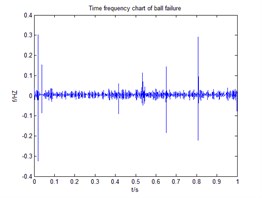
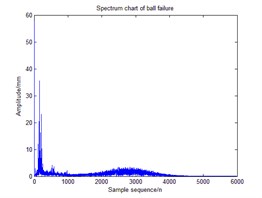
Fig. 2Wigner-Ville distribution

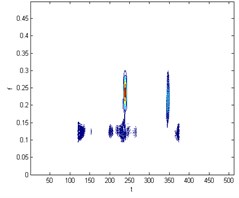
Fig. 3Smoothed Pseudo Wigner-Ville distribution

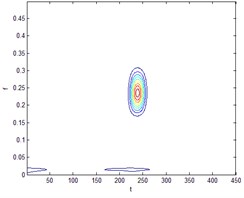
Table 1 is through the smoothed pseudo Wigner-Ville decomposed sub-band samples entropy, Table 2 is through the EMD sub-band samples entropy, can be seen from the following Table 1, a sample of each of the four states of entropy Sample entropy mean different, average sample entropy biggest ball of failure, the inner faults and normal sample entropy mean, outer ring smallest fault, smooth sample entropy change in the same state, and the various state sample entropy not the same, so the use of sample entropy can distinguish between different faults, in each set of sample entropy fault, the sample entropy sample sizes, indicating that the data inside each sub-band structure, complexity and the information they contain, which are not the same these similarities and differences can be demonstrated by the sample entropy sub-bands.

Comparison Tables 1 and 2 show that for the failure and normal case of the ball, the difference between the average entropy of the multi-scale sub-band sample of the ball fault and the normal state is 0.4067, and the average entropy difference of the multi-scale sub-band sample of the ball fault and the normal state is 0.1479 when the smooth pseudo-Wigner-Ville decomposition is used. Obviously, the greater the difference between the recognition the better, So the fault information extraction of smooth pseudo Wigner-Ville is better than EMD.

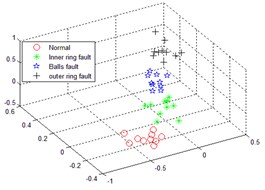
Multi-scale sub-band samples entropy for high-dimensional matrix remodeling, after the reconstruction of the matrix dimensionality reduction were LLTSA, dimensionality reduction dimension is 3-dimensional, neighbors point $K=$ 10, normal, inner ring fault, the balls fault and the outer ring fault four states sequentially dimensionality reduction operation, then the failure to identify the effect of contrast. The following Fig. 4 comes EMD distributed multi-scale sub-band samples entropy and LLTSA recognition renderings; The following Fig. 5 is through smoothing pseudo Wigner-Ville and LLTSA recognition renderings; The following Fig. 6 is only through LLTSA recognition renderings; The following Fig. 7 is through the multi-scale child sample entropy of smoothing pseudo Wigner-Ville distribution and LLTSA recognition renderings.

Fig. 4The recognition renderings of EMD of multi-scale sub-band sample entropy and LLTSA

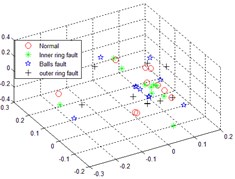
Fig. 5The recognition renderings of Pseudo Wigner-Ville and LLTSA

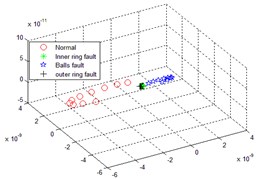
Comparing Fig. 4, 5, 6 and 7, it can be seen that the four states in Fig. 4 are completely mixed together, cannot be completely separated, there is a certain intersection, and there are bad faults in polyethylene, and the fault types cannot be identified; Fig. 5 in normal circumstances can be separated from each other faults, but mixed together with each other among other faults, overlapping, failure is not recognized; Fig. 6 can be separated in four cases substantially, but the inner faults and fault spaced too close to the ball, it is possible to identify process will interfere with each other; Fig. 7, the poly nature is good of the various states, and various fault no overlap part, between the failures can be good recognition, can achieved the fault identification requirements.

Fig. 6LLTSA recognition result

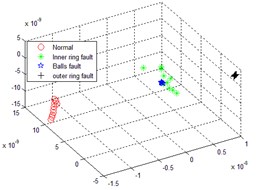
Fig. 7The recognition result of multi-scale sub-band sample entropy of smoothed pseudo Wigner-Ville distribution and LLTSA

6. Conclusions

The results showed that the diagnostic methods of smoothed pseudo Wigner-Ville multi-scale sub-band samples entropy and LLTSA for bearing failure have a good diagnostic effect, and high recognition rate of fault diagnosis, the method can dig main popular structure from fault data, So as to obtain the fault feature better.