Research on fault diagnosis method of bearing based on parameter optimization VMD and improved DBN

1. Introduction

The bearing is widely used in large equipment such as hydro turbines, trains, cranes, etc., and is very important to ensure equipment safety. However, the bearing runs for a long time and is affected by the vibration of other components, which aggravates the occurrence of bearing faults. Effective bearing fault diagnosis can provide support for the stable operation of equipment and has a profound impact on improving equipment utilization and reducing maintenance costs.

Vibration signal analysis is widely used to diagnose bearing faults [1-2]. Traditional time-domain analysis methods cannot effectively diagnose nonlinear and non-stationary bearing vibration signal faults. At present, many modern time-frequency analysis methods have been widely applied in the field of fault diagnoses, such as wavelet transform (WT) [3], empirical mode decomposition (EMD) [4], ensemble empirical mode decomposition (EEMD) [5], empirical wavelet transform (EWT) [6] and variational mode decomposition (VMD) [7]. Zhou [8] used wavelet decomposition combined with the entropy method to diagnose bearing faults. The feature extraction effect was significant, laying the foundation for the subsequent bearing fault diagnosis. The wavelet transform method can deal with non-stationary signals and remove background noise, but the fixed basis function is unsuitable for multi-feature matching. Alexandre Trilla [9] applied the EMD method to diagnose the axle box of the bogie. Cai [10] proposed a rolling bearing failure method based on EMD decomposition and GNN-AdaBoost. Zhao [11] adopted a method based on combining EMD and kernel-related blind source extraction methods to solve the early fault diagnosis of bearings. The experiment proved that this method could extract fault features well under strong background noise. Wang [12] applied the adaptive EEMD algorithm to the denoising process of bearing vibration signals and achieved a good noise reduction effect. Li [13] proposed a combined method based on EEMD and WT analysis, which achieved good diagnostic results. Although EMD can effectively analyze and process bearing signals, it has some problems that affect signal processing accuracies, such as modal aliasing, end effects, and over-and under-envelope. EEMD can effectively suppress the modal aliasing of EMD, but the operation process is complex [14]. Cao [15] applied EWT to diagnose the signal of the bearing. The results showed that EWT performs well in detecting outer ring faults, roller faults, and composite faults of the outer ring and roller. Zhang [16] used the EWT to decompose signal and combine it with envelope analysis for fault diagnosis, which can effectively carry out fault detection. Compared with the EMD, this approach separates the modalities and provides more actionable results. However, EWT is limited by the Fourier spectrum segmentation and the selection of boundary detection methods [17]. For the problems mentioned above, Dragomiretskiy proposed the VMD algorithm. The method can simultaneously estimate the corresponding modes to perfectly balance the errors between them to obtain the separation of different components in the signal while avoiding the end effect and mode aliasing phenomenon. It has superior signal processing capability than EMD, EEMD, and EWT. Li [18] applied the VMD to extract the feature of the signal, and it turns out that VMD has a better feature extraction ability. Hang [19] used VMD and entropy theory to identify bearing faults. It is proved that VMD entropy is effective for bearing fault identification. However, the decomposition result of VMD is constrained by parameter settings. So how to determine VMD parameters is necessary to achieve efficient decomposition of VMD [20]. The research on parameter setting of VMD decomposition of bearing vibration signal has achieved certain achievements. Yan [21] estimated the number of modal components K by scale-space representation and the scale-space spectrum segmentation, optimizing the parameters of VMD. However, this approach is limited by experience. Therefore, the study of VMD parameter settings is of great significance in improving the feasibility of signal processing. The intelligent optimization algorithm provides a helpful idea for VMD parameter setting. The particle swarm optimization (PSO) algorithm has the advantages of easy implementation, high precision, and fast convergence. It is introduced into the VMD parameter setting in this paper.

To better extract fault feature information, information entropy is used for feature extraction. Sample entropy (SE) [22] and permutation entropy (PE) [23] have been applied to extract signal features. Qin [24] applied sample entropy to obtain feature information in bogie signals. Feng [25] obtained the eigenvectors of the bearing by PE calculation. Rostaghi [26] proposed a new method to calculate the complexity of time series data: dispersion entropy (DE). The DE can fully consider the difference between the signal amplitudes and has a faster technical speed. Compared with the other algorithms, it shows tremendous advantages in feature extraction.

The key to bearing fault diagnosis lies in the identification of fault mode. At present, support vector machine (SVM) is a widely used classification algorithm. Compared with random forest and k nearest neighbors (KNN), SVM has the advantages of accuracy and robustness, which have been proved in [27]. SVM has achieved certain results in the field of fault pattern recognition. Zhu [28] combined fuzzy entropy (FE) and SVM to identify bearing fault types. Liu [29] used SVM as the fault classifier of a train bogie braking system and obtained high classification accuracy. María Jesús Gómez [30] proved the effectiveness of SVM. However, the processing ability of SVM in high-dimensional and nonlinear data is limited. DBN is a deep learning method that can effectively reduce the interference of high-dimensional data on SVM and is widely used as a pattern recognition algorithm. He [31] effectively detects weak faults of rolling bearings using DBN. Zhong [5] used DBN as a pattern recognition algorithm in circuit intermittent fault diagnosis and achieved a high fault diagnosis rate. However, the classification effect of DBN is affected by the number of hidden layers and learning rate. Currently, most DBN algorithms determine the network structure by experience, and the classification effect is not guaranteed. Therefore, how to reasonably determine the parameters, such as the number of nodes in the hidden layer of DBN and the learning rate, is of great significance in improving the classification accuracy of DBN.

Based on the above research, when the VMD processes the bearing vibration signal, there is a problem in that the VMD parameter setting leads to a poor decomposition effect. During bearing fault classification, the recognition accuracy of DBN is affected by parameters. Therefore, combining VMD discrete entropy and PSO-DBN establishes a new method for bearing fault diagnosis. Firstly, PSO-VMD is used to improve the VMD decomposition effect. The optimized VMD is utilized to process the signal and compute the DE of the components to obtain the eigenvectors. Then, a PSO-DBN model is established to improve the accuracy of DBN recognition. Finally, use the PSO-DBN model to diagnose bearing fault types. Research shows that the method can accurately judge bearing faults and has certain advantages compared with similar existing methods. The contributions are as follows:

(1) A signal processing method of PSO-VMD is proposed to solve the VMD parameter optimization problem.

(2) Combining DE with VMD for signal feature extraction improves the effect of feature extraction.

(3) PSO-DBN is proposed to solve the problem of DBN parameter setting and improve the accuracy of fault diagnosis.

2. Methods

2.3. PSO optimization DBN

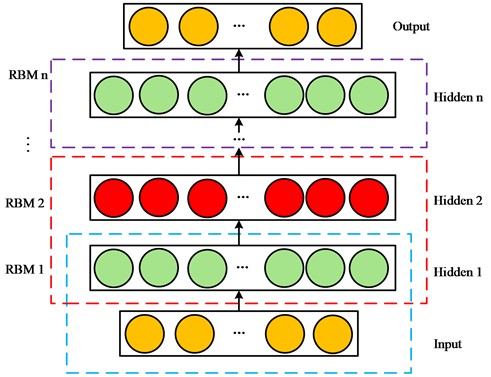
DBN composes multiple restricted Boltzmann machines (RBM), and each layer of the RBM network is composed of multiple neurons, such as in Fig. 1. The layers are connected by weight. The super parameter setting of DBN is usually set according to experience, which restricts the classification accuracy of the algorithm. This paper takes the highest classification accuracy of the training set as the goal and uses PSO to optimize the algorithm to obtain DBN. The detailed steps are as follows.

Fig. 1DBN structure

Step 1. Initialize particle swarm. Initialize the position $X_i^{k=0}$ and velocity of particles $V_i^{k=0}$.

Step 2. Fitness value calculation. Calculate the fitness value of each particle to find the best particle in this round $X_{gbest}^k$ and the best particle in search history $X_{pbest}^k$.

Step 3. Update the velocity and position of the particles. The velocity and position of the particles are updated using formulas $X_I^{k+1}=X_i^k+V_i^{k+1}$ and $V_i^{k+1}=w{V}_i^k+c_1{r}_1\left(X_{ipbest}^k-X_i^k\right)+c_2{r}_2\left(X_{igbest}^k-X_i^k\right)$. Where $w$ is the inertia weight, the range is [0, 1], $c_1$ and $c_2$ are acceleration parameters, $r_1$ and $r_2$ are two random values that change in the range of [0, 1].

Step 4. If the misclassification rate of training samples meets the set conditions or reaches the set number of iterations, the PSO cycle ends. Otherwise, go to step 2, $K=K+1$, and repeat steps 3 and 4 until the conditions are met.

Step 5. Using the trained DBN network training test data, output bearing classification results.

2.4. Fault diagnosis method based on VMD dispersion entropy and PSO-DBN

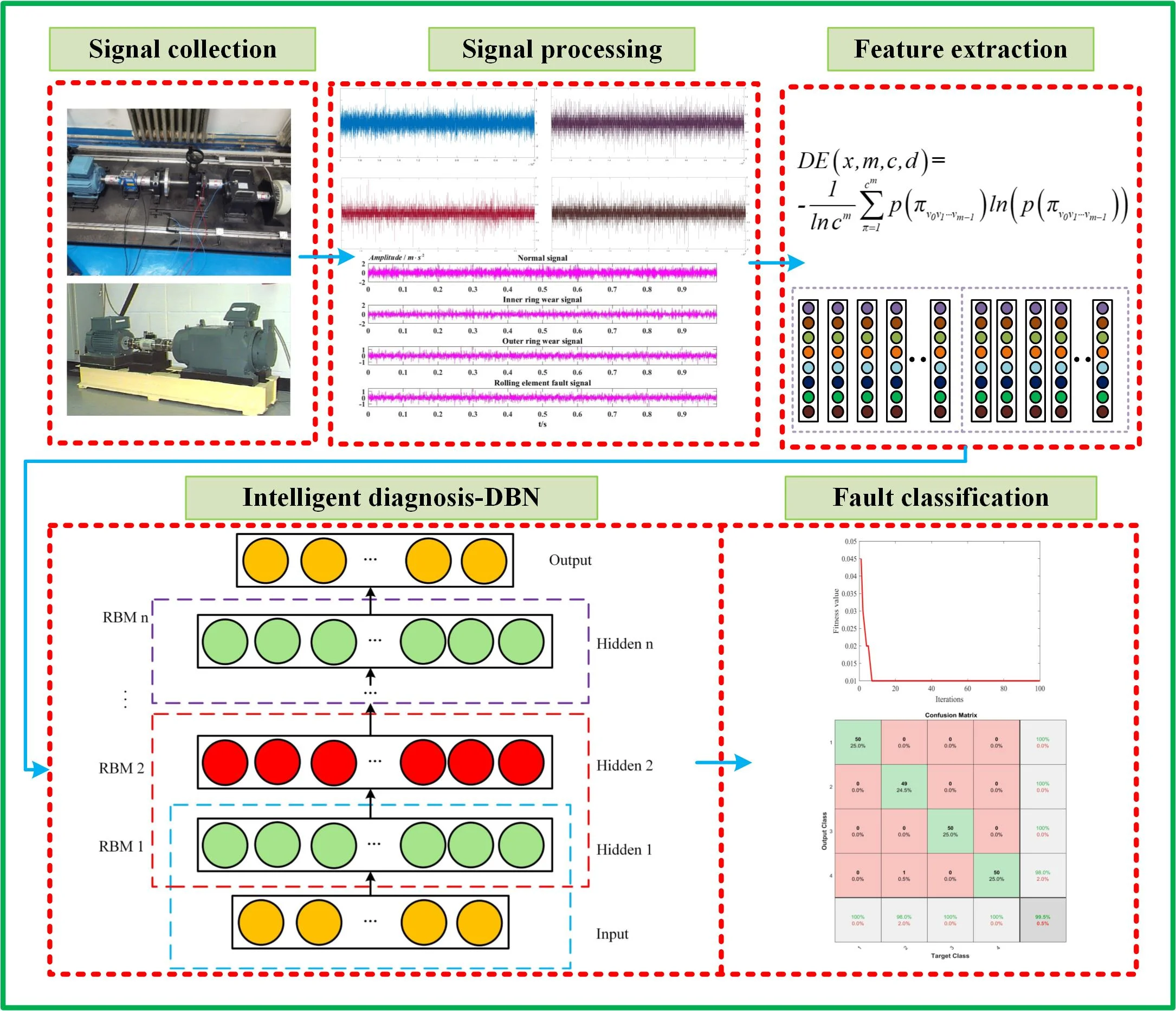
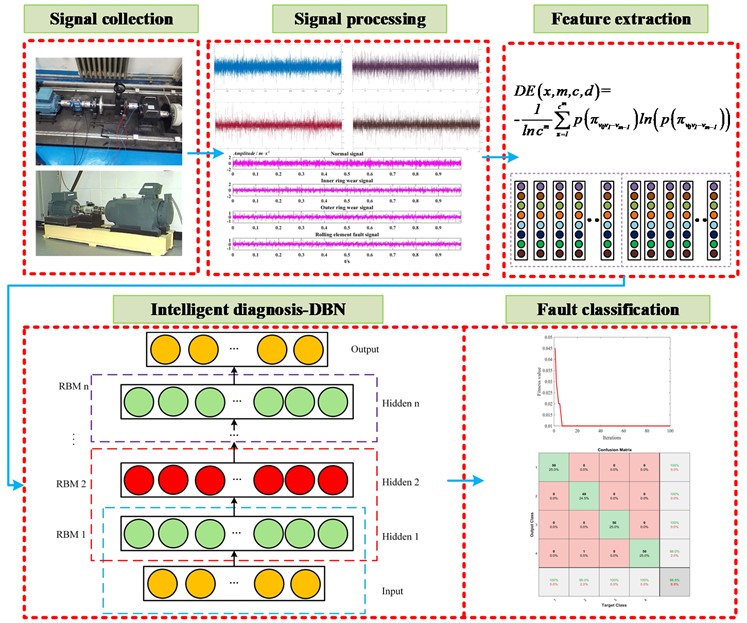
A bearing fault diagnosis method based on VMD-DE and PSO-DBN is proposed to effectively judge the type of bearing failure, which has good fault diagnosis ability. The main steps are shown in Fig. 2:

Step 1: Build bearing fault simulation test bench, collect bearing vibration signal.

Step 2: PSO is used to optimize VMD parameters to obtain VMD parameters $\left[K,\alpha \right]$.

Step 3: The original vibration fault data is decomposed into a series of IMFS by VMD.

Step 4: Calculate the dispersion entropy of IMFS, construct the feature matrix, and divide the test set and training set.

Step 5: The PSO is utilized to optimize the parameters of DBN to obtain the optimal penalty coefficient and kernel function. The PSO-DBN model is used for the fault diagnosis of bearing.

Fig. 2Fault diagnosis process based on VMD-DE and PSO-DBN

3. Experimental analysis

3.1. Case study 1

3.1.1. Data collection

We use the Windows 10 system, and the processor is Intel(R) Core (TM) i5-8250U CPU @ 1.60 GHz 1.80 GHz, running on the Matlab2020. The bearing fault diagnosis platform collects the bearing vibration signals. The experiment uses the bearing fault diagnosis platform shown in Fig. 3. Fig. 3 is a photo taken by experimenters in the laboratory, including the motor, coupling, bearings, gearbox, and sensors. The speed is set to 1200 r/min, and the sampling frequency is set to $F_s=$ 10240 Hz. The bearing parameters are shown in Table 1. Moreover, the characteristic frequency of various fault types can be calculated by bearing parameters. Collect the signals of the four states of the bearing, each vibration type includes 24 samples, and each sample has 10240 sampling points. The vibration signals of the bearing collected under four test conditions are shown in Fig. 4. The signal amplitudes of the four states are small and have no high-frequency periodic characteristics. Therefore, it is impossible to discern bearing fault type through time-domain waveform diagram intuitively.

Fig. 3Bearing fault diagnosis platform

Fig. 4Time domain waveform

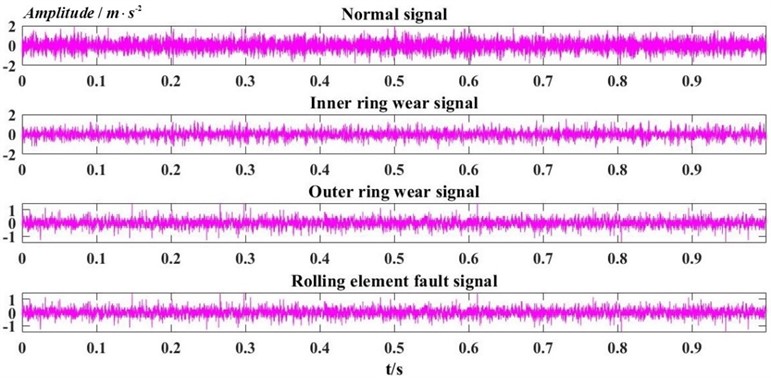
Table 1Bearing parameters

Model	Bearing pitch diameter / mm	Roller diameter / mm	Number of rolling elements	Contact angle / (°)
6308	65.5	15	8	0

3.1.2. Fault diagnosis

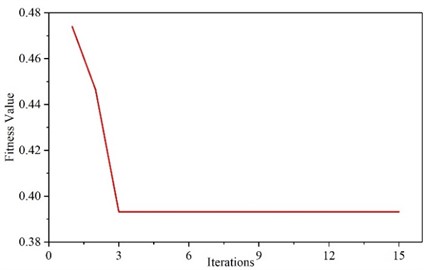
According to the fault diagnosis process shown in Fig. 2, the VMD parameters should be optimized first by using the PSO. The quantity of populations is set as 30, the quantity of iteration steps is 15, and the PSO is. Taking a set of vibration signals, for example, the iterative curve is shown in Fig. 5. The best result is obtained on the third time, indicating that the algorithm has fast convergence speed and strong global optimization ability, which is suitable for VMD parameter optimization. After the third iteration, the fitness value of 0.393 is the smallest and reaches optimal. It shows that the optimization algorithm has good performance, suited to the optimization VMD parameter, and the corresponding parameter is 8,2382.

Fig. 5PSO optimization of VMD parameter convergence curve

The modal components with rich fault information are selected for envelope spectrum demodulation analysis to characterize the fault characteristics better. Peak index is a statistical index used to detect whether there is an impact in the signal; Kurtosis is an index to evaluate fault impact and is sensitive to impact signal. If the kurtosis index and kurtosis value are large, it is proved that the signal contains rich fault information. The components with a large kurtosis index and kurtosis value were selected as the best components in this paper. The parameter-optimized VMD is utilized to process the vibration signal, and each component’s peak index and kurtosis value are calculated. Table 2 shows the calculation results. The peak index and kurtosis value of IMF4 are the largest, so the IMF4 component is determined as the best component. Draw the envelope spectrum of the IMF4 component, as shown in Fig. 6. Table 1 shows the bearing roller fault characteristic frequency $f=$ 41.38Hz. A clear peak line at fault characteristic frequency $f_1$, the double $f_2$, and the triple frequency $f_3$ are in Fig. 5. Therefore, it can be concluded that there is local damage in the bearing roller, and the analysis results are consistent with the actual situation.

Table 2Peak index and kurtosis value of IMF component.

Index	IMF1	IMF2	IMF3	IMF4	IMF5	IMF6	IMF7
Peak index	1.26	1.35	1.66	1.82	1.47	1.40	1.17
Kurtosis value	3.01	3.21	3.56	3.64	3.55	3.26	3.07

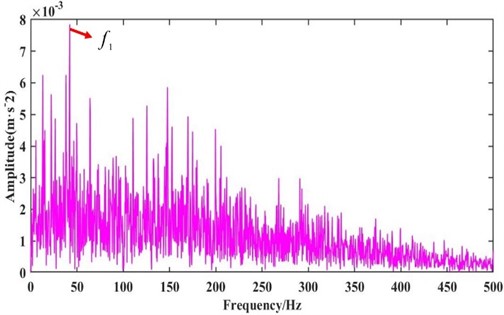
To verify the feasibility of PSO- VMD, the traditional VMD method and EMD method are used to process the signal of the rolling element. Then the optimal component is selected to draw the envelope diagram for observation and comparison. The traditional parameter setting method of VMD is the center frequency method, as shown in Table 3. when $K=$ 9, the central frequencies of IMF8 and IMF9 components are relatively close, which may lead to modal mixing. Therefore, $K$ is selected as 9, and the penalty factor is set as 2000. Then decompose the signal and select the best component to draw the envelope diagram, as shown in Fig. 7. The envelope diagram of the optimal component after EMD decomposition is shown in Fig. 8. There is a clear peak spectrum at the characteristic frequency $f_1$ of the rolling element fault. However, modal aliasing is at the double $f_2$ and triple frequency $f_3$. Through the above analysis, it can be known that the method of optimizing the VMD parameters using the PSO algorithm makes the eigenfrequencies of the optimal component envelope spectrum significant.

Table 3The center frequency of IMFS /Hz

$K$	IMF1	IMF2	IMF3	IMF4	IMF5	IMF6	IMF7	IMF8	IMF9	IMF10
6	328	1101	1962	2813	3633	4445
7	282	953	1763	2543	3299	3884	4605
8	248	827	1521	2208	2882	3527	4019	4683
9	212	685	1331	1958	2557	3126	3651	4306	4702
10	202	638	1210	1777	2324	2865	3381	3803	4386	4793

Fig. 6Optimal component envelope diagram after VMD optimization

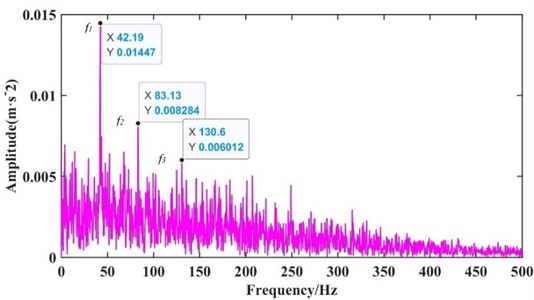
Fig. 7Traditional VMD optimal component envelope graph

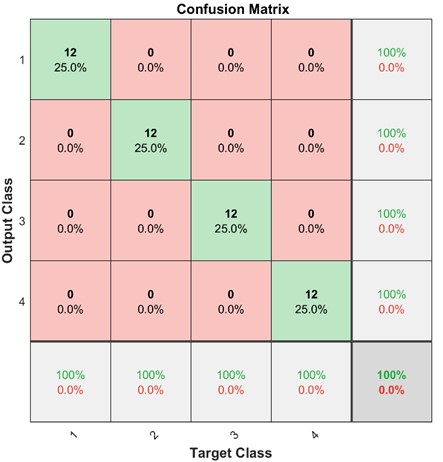
In order to further judge the bearing failure, firstly, the parameters of the inner ring fault, outer ring fault, and normal signal are obtained by using PSO to optimize VMD. Then, the optimized VMD is applied to process the signal to obtain the IMF component and compute the DE of the components to construct the eigenvectors. The PSO is applied to optimize the DBN parameters with the goal of the minimum diagnostic error rate of the train set, the population size is set to 30, and the maximum quantity of iterations is 30. The optimal range of DBN parameters is [1, 100], and the obtained DBN parameters are [19 15 8]. A total of 96 groups of sample data, 48 groups were selected as training data, and 48 groups were selected as test data. Fig. 9 is the diagnosis results of the PSO-VMD-IDBN method under four different fault states. The accuracy of the method for bearing fault diagnosis reaches 100 %. Therefore, it can be proved that the method has high reliability and strong feasibility in judging bearing faults.

Fig. 8Envelope spectral value of EMD optimal component

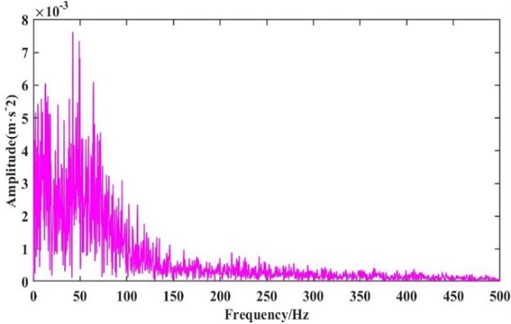
Fig. 9Fault diagnosis results

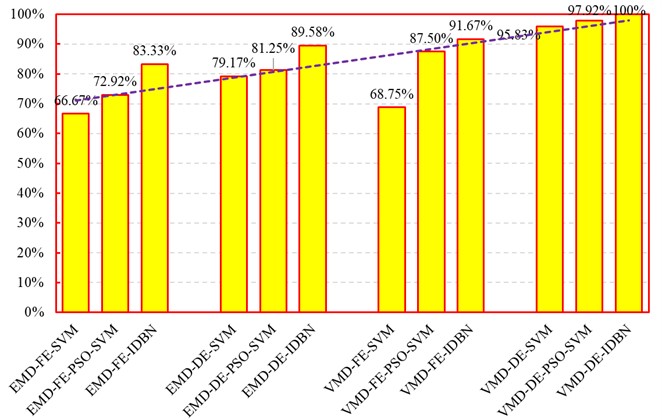
Eleven fault diagnosis methods are selected for comparison to prove the superiority of the method. Fig. 10 shows the fault identification accuracy. The fault diagnosis methods are divided into four groups. In the first group of fault diagnosis methods, EMD is used to process signals, and FE is utilized to extract fault feature information. SVM, PSO-SVM, and PSO-DBN proposed in this paper are used as the diagnosis method for comparison. The recognition rate of PSO-DBN is higher than PSO-SVM and SVM, but only 83.33 %. The second group of fault diagnosis methods takes the DE as the feature vector, and the vibration signal decomposition algorithm and diagnosis method are the same as the first group. The highest recognition rate of the EMD-DE-IDBN method is 89.58 %, which proves the effectiveness of the PSO -DBN. Compared with the first group of fault diagnosis results, the vibration signal decomposition method and fault diagnosis method are the same. The feature vector represented by the DE is better than that represented by the FE. In the third group of fault diagnosis methods, the optimized VMD method is applied as the signal decomposition method. The method for characterizing the feature vector and the pattern recognition method are identical to those in the first group. The highest diagnostic rate of the VMD-FE-IDBN method is 95.83 %, which proves the superiority of the PSO to optimize DBN. By comparing with the first group of fault diagnosis results, it is proved again that the PSO algorithm optimized VMD vibration signal decomposition method is better than the EMD, which is the same as the above analysis result. In the fourth group of fault diagnosis methods, the PSO algorithm is used to optimize VMD as the vibration signal decomposition algorithm. The dispersion entropy is used to characterize the fault characteristics. SVM, PSO-SVM, and PSO-DBN are applied for fault diagnosis. The VMD-DE-IDBN method proposed has the best diagnostic effect, and the diagnostic rate reaches 100 %. By comparing with the results of the third group of fault diagnoses, it is proved again that using the DE as the feature vector is superior to using the FE to characterize the feature vector. Compared with the results of the second group of fault diagnosis, the PSO-optimized VMD method proposed in this paper is proven effective in decomposing bearing vibration signals. From the above discussion, the parameter optimization VMD DE and PSO-DBN method for bearing fault diagnosis have significant advantages. Compared with other methods, they have obvious advantages in the single vibration signal decomposition method, feature vector representation method, pattern recognition method, and overall fault diagnosis method, which can reliably determine bearing faults. Therefore, the method proposed is suitable for bearing diagnosis.

Fig. 10Comparison of different diagnostic methods

3.2. Case study 2

In order to verify the generalization and robustness of the method, the bearing data collected by Case Western Reserve University are used for verification [32]. The experimental platform is shown in Fig. 11, including motor, torque sensor, and power tester. The drive end bearing used here, the model is SKF6205, the damage of the bearing is single point damage by EDM, and the damage diameter is 0.1778 mm. The state of the bearing is divided into normal, outer ring fault, inner ring fault, and rolling element fault. The sampling frequency is 12 KHz. Select 2048 sampling points as a sample, and each type has 48 samples.

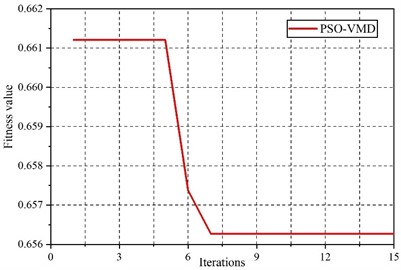
PSO is applied to optimize the parameters of VMD, such as the rolling element fault. Fig. 12 shows the optimization curve. The optimal fitness value is 0.6562 at the 7th optimization, and the output VMD parameter is 2175,7. The algorithm has fast optimization speed and accuracy and can realize VMD parameter optimization. The conclusion is consistent with the previous conclusion, which shows high reliability. Optimized VMD for processing vibration signals, then the DE extracts the feature. A total of 96 groups of feature vectors are extracted. Forty-eight groups of them are selected as the training set, and the rest are selected as the test set. The PSO-DBN is applied as the diagnosis algorithm for fault pattern recognition. The same parameters are set as above, and the diagnosis results are obtained in Fig. 13. The fault diagnosis accuracy is 100 %, consistent with case 1. It shows that the proposed method has excellent generalization and robustness, which can provide theoretical guidance for bearing fault pattern recognition.

Fig. 11Case Western Reserve large bearing fault diagnosis test bench

Fig. 12Iterative optimization graph is a figure

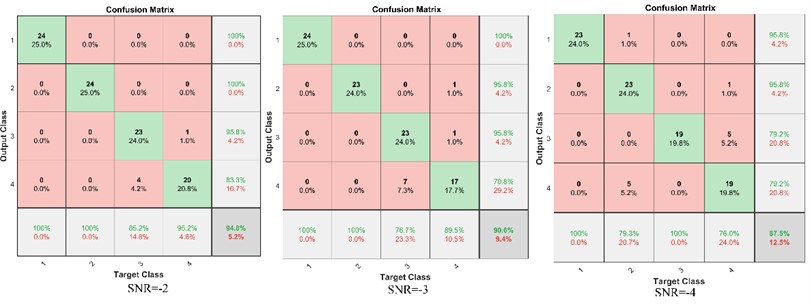
The data collected in the laboratory are often pure signals, and the actual operation of the signal usually contains a lot of noise, affecting the accuracy of fault diagnosis. In order to further verify the robustness of the method, this paper chooses to add Gaussian white noise with signal-to-noise ratio (SNR) of –2, –3, and –4 to the original signal, respectively. Taking normal data as an example, the time-domain waveform after adding noise is shown in Fig. 14. It can be seen from Fig. 14 that the signal without noise has the characteristics of periodic impact. With the increase of the intensity of Gaussian white noise, the periodic impact is gradually submerged. That is, the characteristics of the signal are gradually submerged, which brings great challenges to fault diagnosis. In order to verify the robustness of the proposed method in fault diagnosis under strong noise background, the characteristics of signals under different Gaussian white noises are extracted according to the process of fault diagnosis in Section 2.4, and the feature vectors are constructed. Finally, the optimized DBN is used for classification. The results are shown in Fig. 15. It can be seen from Fig. 15 that as the intensity of Gaussian white noise increases, the accuracy of fault diagnosis gradually decreases, indicating that Gaussian white noise has a great influence on fault characteristics. In fact, even when SNR = −4, the proposed method can still maintain a high accuracy of 87.5 %, indicating that the proposed method has good robustness.

Fig. 13Case Western Reserve University bearing fault diagnosis results

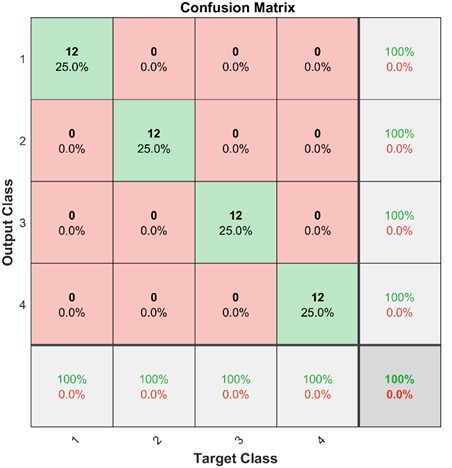
Fig. 14Time domain waveforms with different SNR

Fig. 15Fault diagnosis results under different SNR

4. Conclusions

Given the influence of the vibration of other parts and environmental noise on the bearing, the vibration signal is nonlinear and non-stationary, which makes it hard to obtain the fault characteristics. A parameter optimization VMD dispersion entropy and PSO-DBN-based bearing diagnosis method are presented. Firstly, with FE as the fitness value, the PSO algorithm is used to optimize the VMD parameters to obtain the parameter $\left[K,\alpha \right]$. The optimized VMD is used for signal decomposition to obtain $K$ modal components. Then, the dispersion entropy of $K$ modal components is calculated as the feature vector; Finally, DBN is optimized by the PSO and used as a pattern recognition method for pattern recognition. The method can accurately identify the faults of different bearing states, and the recognition rate reaches 100 %. The contribution mainly includes the following aspects:

(1) A signal processing method of PSO-VMD is proposed, which solves the problem of the limited decomposition effect of VMD. Compared with the traditional VMD method and EMD method, this method can effectively overcome the problem of modal aliasing, and the signal processing effect is better.

(2) A feature extraction method based on DE is proposed, which improves the effect of feature extraction and has more significant advantages than FE and SE.

(3) A fault pattern recognition algorithm of PSO-DBN is proposed, which effectively improves the accuracy of bearing fault diagnosis.

(4) The proposed parameter optimization VMD discrete entropy and PSO-DBN bearing fault diagnosis method have high fault diagnosis rates. It can provide theoretical references for fault diagnosis of bearings and other rotating machinery.

Although the proposed method can effectively extract the characteristic frequency of the signal, when the background noise is enhanced, it may lead to feature submergence. Therefore, the study of signal noise reduction significantly improves fault diagnosis accuracy.