Abstract
In view of the fact that the traditional study of the chain breaking condition of the scraper conveyor only considers the case of two-way simultaneous chain breaking, this paper mainly studies the single-side chain breaking condition and its influence on the longitudinal vibration and swing vibration characteristics of the scraper chain system. Using the tension calculation principle of the point-by-point tension method, each section of the scraper in the study area is taken as a unit. A coupled dynamic model of longitudinal and oscillating vibration of scrapers is established and connected with Voigt model. The dynamic response laws of the longitudinal and oscillating vibration of the scraper before and after the chain fracture under different transportation conditions are numerically simulated. The calculation results show that when there is material behind the broken chain, the longitudinal tension of the chain and the oscillating vibration of the scraper reach the maximum value, and the chain speed fluctuation reaches 543.1 % compared with the normal operating conditions. Only when there is material in front of the broken chain, the longitudinal tension mutation of the chain and the oscillating vibration value of the scraper are weaker than those of the previous working conditions. When there are materials at the front and back of the broken chain, the sudden change of the longitudinal tension of the chain and the oscillating vibration value of the scraper are the minimum, but they also reach twice the normal working condition, and the chain speed fluctuation reached 194.4 %. The research results of this paper provide a theoretical basis for grasping the operation status of the scraper conveyor in the coal mine and predicting the life of the scraper conveyor.
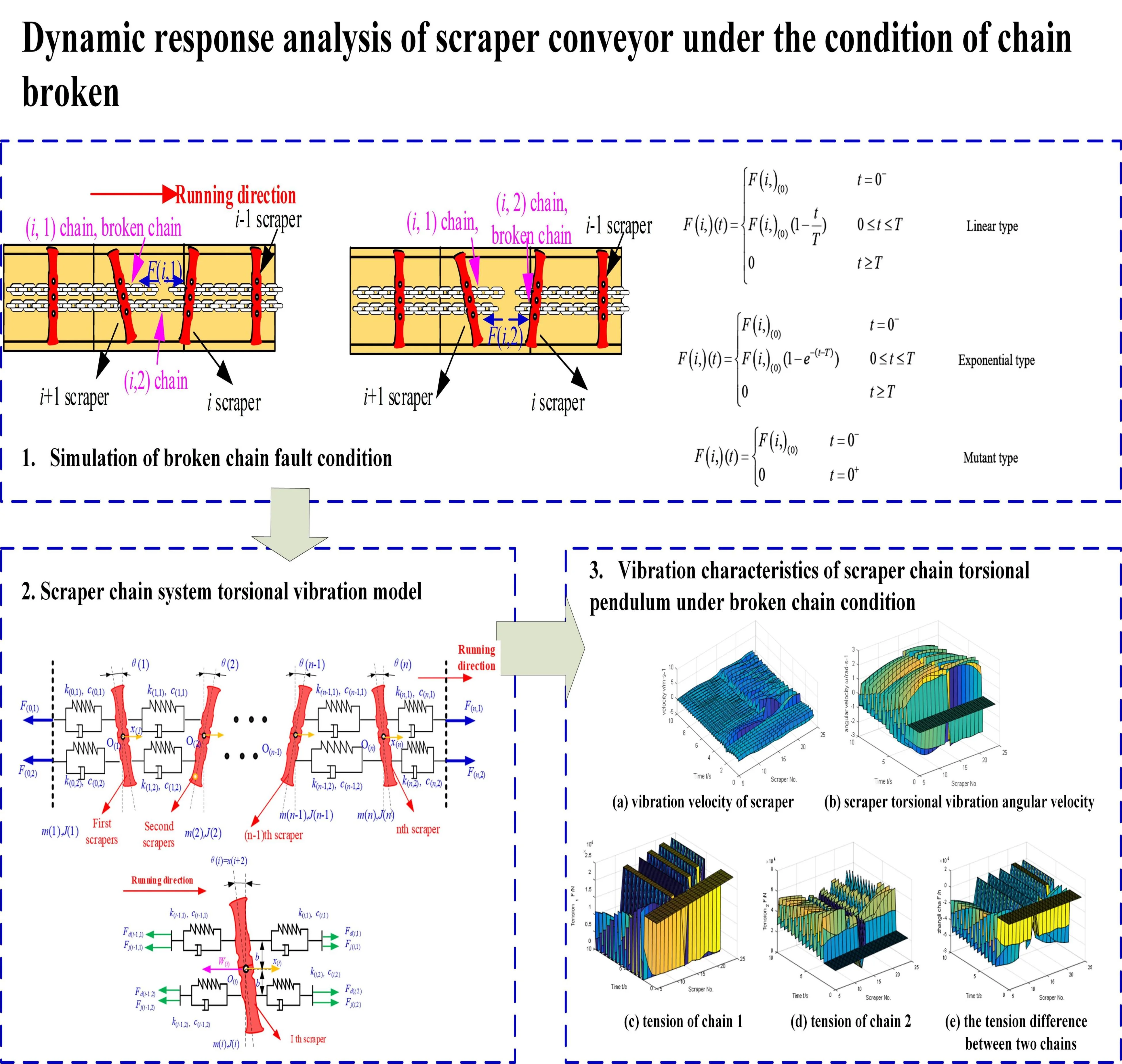
Highlights
- When there is material behind the broken chain, the longitudinal tension of the chain and the oscillating vibration of the scraper reach the maximum value, and the chain speed fluctuation reaches 543.1%.
- Only when there is material in front of the broken chain, the longitudinal tension mutation of the chain and the oscillating vibration value of the scraper are weaker than those of the previous working conditions.
- When there are materials at the front and back of the broken chain, the sudden change of the longitudinal tension of the chain and the oscillating vibration value of the scraper are the minimum, but they also reach twice the normal working condition.
1. Introduction
The material on the scraper conveyor is usually loaded unevenly [1-2]. Under the influence of non-uniform load, the scraper will swing around the center of the chain, so that a chain has a large force and a chain has a small force. In this way, the stressed chain may exceed the safe load [3].
Zhang [4] studied a new method to calculate the chain tension distribution of scraper conveyor based on multi-body rigid-flexible coupling dynamics method. Jiang [5-6] studied a new dynamic monitoring method of scraper conveyor. This method can calculate and analyze the dynamic characteristics of scraper conveyor by real-time monitoring the rotating speed of scraper conveyor head and tail. Zhang [7] constructed the dynamic model of the chain transmission system of the scraper conveyor by using the virtual prototyping technology, and obtained the meshing performance between the chain and the sprocket of the scraper conveyor under different working conditions, as well as the dynamic fluctuation law of chain tension. Dolipsk M. [8] studied the calculation method of dynamic load of scraper conveying in longwall mining, and simulated the running load of scraper conveyor by computer. Wang [9] made an in-depth study on the chain tension dynamic monitoring device of the heavy scraper conveyor in coal mine, and realized the real-time dynamic monitoring of chain tension fluctuation. In order to study the wear of the middle groove of the scraper conveyor under different working conditions, Xia [10] uses the discrete element method to establish the dynamic response analysis model of the coupling between the scraper conveyor and the coal. In references 11 to 14, scholars have studied dynamic modeling and simulation, which provides a reference basis for modeling and numerical calculation in this paper [11-14].
Scraper conveyor chain card failure, the scraper will produce torsion pendulum, the two chains caused by uneven stress. Therefore, when the torsion pendulum is produced in the scraper chain system, it may cause a chain force and the other chain is not subjected to force, so the chain of force may exceed the safety load and the scraper conveyor appears. A frequent broken chain accident. In this paper, the coupling dynamic model of longitudinal vibration and swing vibration of scraper conveyor chain is studied, and the influence of chain breaking condition on the longitudinal vibration and swing vibration of scraper conveyor chain is analyzed.
2. Simulation of broken chain fault condition
Abnormal load condition refers to the sudden increase of material on the conveyer, such as the rib spalling or the conveyer chain being jammed, the material bolt formed when material on the free-load side is too much, a large material jams when the chain passes through the crusher or the shearer, as shown in Fig. 1. This situation is sometimes impossible to be predicted and unavoidable. In the design phase, the analysis of the dynamic characteristics under this condition is of great significance to ensure the normal operation of the conveyor, and also provides a theoretical basis for the study of monitoring instruments for such conditions.
Fig. 1Chain broken and chain blocked on scraper conveyor
When on the scraper conveyor, the first chain behind the th scraper conveyor is broken suddenly, the scraper has only one chain to drag and pull, and the scraper will be subjected to a non-uniform load. If a chain breaks suddenly and the scraper conveyor fails to respond and stops in time, the other chain also breaks because of overload. At this moment, the scraper, chain, and materials behind the th scraper will accumulate because of the loss of traction. Then the th scraper will cause a sudden decrease on the tension of the front chain because of the loss of the rear load. The mechanism of scraper biasing when the chain breaks is shown in Fig. 2.
Fig. 2Mechanism of bias load of scraper when chain broken
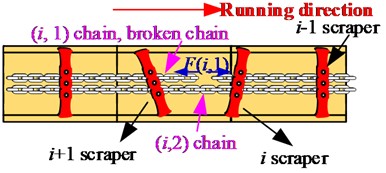
a) Chain broken on unilateral chain
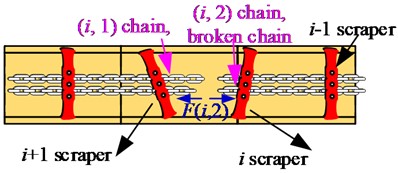
b) Chain broken on bilateral chain
The abnormal load of a chain when it suddenly breaks can be simulated in the following ways.
Linear type:
Exponential type:
Mutant type:
3. Scraper chain system torsional vibration model
3.1. Scraper chain system with dynamic modeling
Using the tension calculation principle of the point-by-point tension method, and the model used is Voigt model. Each section of the scraper in the study area is taken as a unit. The stiffness coefficient k in the model can be expressed as:
To simplify the model, make the following assumptions:
(1) At the beginning of the study, the scraper chain has a certain initial tension.
(2) The mass of the chain is distributed to the scraper, but the moment of inertia of the scraper is not affected.
(3) The stiffness of the middle slot is very large, so it will not vibrated.
(4) The influence of the stiffness difference of the chain caused by structural factors on the torsional vibration of the scraper chain system is ignored.
Fig. 3Dynamic model of scraper conveyor in study area
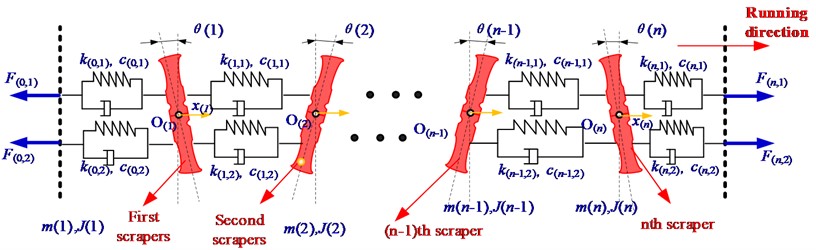
Based on the principle of point-by-point tension method, each scraper in the study area is taken as a unit. The dynamic models of n scrapers in the study area are established and connected by Voigt model. The dynamic model established in this paper fully takes into account the friction between the scraper and the middle groove and the force between the scraper and the coal body. The schematic diagram of the dynamic model is shown in Fig. 3 [15].
Take out a single scraper unit and analyze its stress state as shown in Fig. 4.
Fig. 4Mechanical analysis of scraper
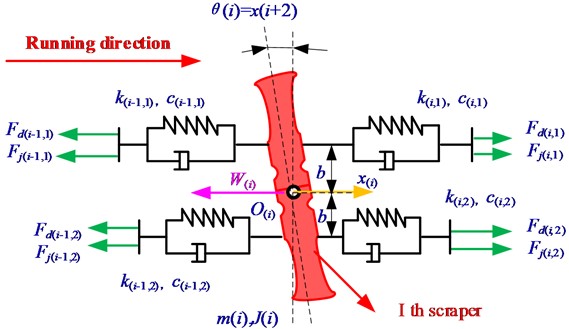
According to the establishment of the analysis model of the scraper chain system and the force analysis in the above figure, the equation of the motion state of the scraper in the scraper chain system can be established. The differential equations of motion are established for the th scraper:
In the form:
3.2. Dynamic simulation research model
The dynamic equation and state equation are established by using Matlab software, that is, a function subroutine is constructed for the dynamic equation established above, and the preprocessing of dynamic analysis is realized. The state function of the kinetic equation established above is:
In motion equation of motion, the calculation of dynamic tension is as follows:
When considering damping, the computation of and is considered:
With regard to the handling of a chain that cannot be compressed, order that:
That is to say, when the chain tension is negative, the stiffness of the chain is zero.
The main parameters of the dynamic characteristic simulation model are as follows: SGZ1000/1050 scraper conveyor and MG500/1130-WD shearer as the research object. The length of the scraper conveyor 240 m (head and tail drive chain wheel installation center distance); rated transport capacity 2000 t/h; rated chain speed of scraper 1.25 m/s; conveyor dip angle beta = 0 degree; middle slot length 1.5 m; middle slot width 1 m; middle trough trough height 0.122 m; middle slot allowed corner [alpha] = 1 degrees; conveyor horizontal propulsion step distance 0.8 m; Scraper chain per meter length weight 0.95 kN/m; loose coal density =1000 kg/m3; 38×137 double chain .
The dynamic tension of the chain can be expressed as the product of the dynamic expansion of the chain and the stiffness coefficient of the chain. In order to make the calculation results more accurate, the length of the scraper along the line and its influence on the dynamic expansion of the chain in the process of scraper torsion pendulum cannot be ignored. The following is the process of calculating the dynamic expansion of the chain in the process of scraper torsional pendulum:
The main results are as follows: (1) First consider a relatively simple special case, and then further extend to a more complex arbitrary case.
Assuming that only the th scraper produces a torsional pendulum around the center , the expansion of the chain on the left and right sides of the th scraper and the angle between the left and right side of the chain and the running direction of the scraper are studied. The simplified analysis model is shown in figure.
Considering the simplified analysis model shown in figure, the expansion of the root chain and the angle relative to the running direction of the scraper are analyzed. Suppose the connection point between the root chain and the th scraper is point A, and after the th scraper produces a torsion pendulum at –th angle, the connection point between the root chain and the -th scraper is Ax, and the length of the line segment AAx and the angle A between the line segment AAx and the running direction of the scraper can be calculated by the isosceles triangle AAx with the vertex angle :
Fig. 5Simplified analysis model of chain scraper twist the expansion amount
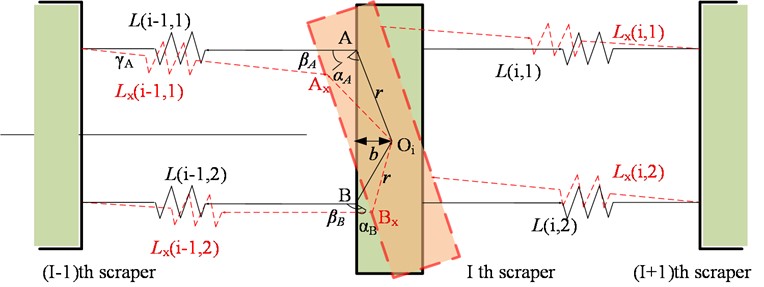
a) Only the -th scraper produces a torsional pendulum
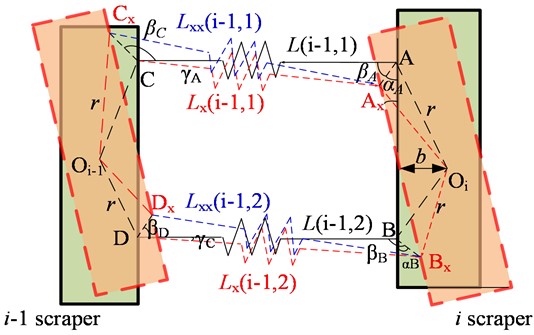
b) Consider that both the th scraper and the th scraper produce a torsional pendulum
Then according to the triangular cosine theorem, the length of the chain and its angle with the running direction of the scraper can be obtained:
where is the displacement difference between the th scraper and the th scraper center, .
Then the expansion of the root chain and the angle relative to the running direction of the scraper are analyzed.
Suppose the connection point between the root chain and the th scraper is the B point, and after the th scraper produces the torsion pendulum at – angle, the connection point between the root chain and the th scraper is Bx, and the length of the line segment BBx and the angle B between the line segment BBx and the running direction of the scraper can be calculated from the isosceles triangle BBx with the top angle :
Then according to the triangular cosine theorem, the length of the chain after the scraper torsion pendulum and its angle with the running direction of the scraper can be obtained:
The calculation method of chain is the same as that of chain , and the calculation method of chain is the same as that of root chain.
(2) Next, when the th scraper and the th produce a torsional pendulum around the center at the same time, the expansion of the chain on the left and right sides of the th scraper and the calculation method of the angle between the scraper and the running direction caused by the swing of the scraper are further considered. the simplified model is shown in Fig. 5(b).
First of all, after the th scraper produces – torsional pendulum angle, the expansion amount of the th chain and the angle relative to the running direction of the scraper are analyzed. Suppose the connection point between the chain and the th scraper does not produce a torsional pendulum, and after the th scraper produces a torsional pendulum at the angle of –, the connection point between the th and the th scraper is the length of the line segment and the angle between the line segment and the running direction of the scraper:
Then the length of can be obtained according to the triangle cosine theorem:
By the same token, if the connection point between the chain and the th scraper does not produce a torsional pendulum, and after the th scraper produces a torsional pendulum at the angle of –, the connection point between the th and the th scraper is the length of the line segment:
4. Vibration characteristics of scraper chain torsional pendulum under broken chain condition
When on the scraper conveyor, the first chain behind the th scraper conveyor is broken suddenly, the scraper has only one chain to drag and pull, and the scraper will be subjected to unbalanced load. If a chain breaks suddenly and the scraper conveyor fails to respond and stops in time, the other chain also breaks because of overload. At this moment, and the scraper and chain and materials behind the th scraper will accumulate because of the loss of traction. Then the th scraper will cause a sudden decrease on the tension of the front chain because of the loss of the rear load. This section will use the scraper chain system dynamic analysis model to analyze the dynamic characteristics of the scraper chain system. At this time, four divided situations will be discussed. The first is the situation where there is no material in both front and rear scraper at the chain breaking sites. This kind of situation usually occurs in the case of the conveyor running with free load or no material in a longer area; The second is the situation where there is material in the front and rear of scraper at the breaking sites, and in which the breaking sites are just in the flow of materials; The third is that there is a material in front of the scraper at the breaking site while no material in the rear. In this situation the breaking site is in the rear of the material flow; The fourth situation is that no material is in front of the scraper at the breaking site while there is a material in the rear, in which the breaking site is in the front of the material flow.
4.1. Dynamic response of scraper chain system without material in front and rear
First of all, aiming at the broken chain, under the condition that there is no material, the dynamic analysis model of the coupling of scraper torsional vibration and chain longitudinal vibration is established, as shown in Fig. 6. The number of scrapers in research area is 30, that is, 30. Set, at the 15th scraper, the chain breakage is simulated.
Fig. 6Schematic diagram of working condition at the front and rear of the chain fracture without coal body
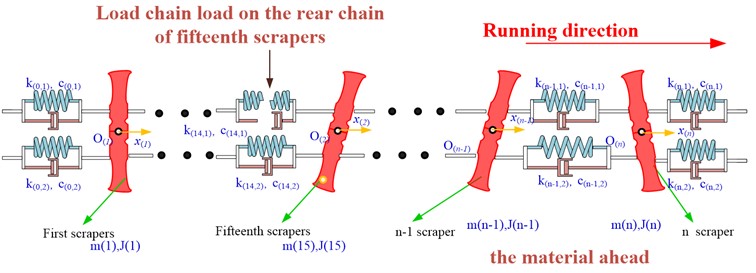
In order to simulate the sudden chain breaking, the tension of the target chain breaking chain is suddenly set to zero in the MATLAB software. The response characteristics of the dynamic model are shown in Fig. 7.
The simulation results show that the chain break will cause the sudden change of the running speed of the scraper before and after the chain break, the torsion of the scraper around the center of the chain and the fluctuation of the tension of the two chains. At the time of chain breaking, the running speed at the front of the chain is increased to 632.4 of the stable speed, and the speed of the scraper at the front of the chain will first drop and then rise, fluctuate repeatedly, and finally close to zero. When the chain breaks, the tension of chain 1 will immediately be zero, that is, the chain breaks and the tension disappears. After chain breaking, the tension of chain 1 fluctuates greatly, and the tension of chain 1 is less than that before chain breaking. At the time of chain breaking, the tension of chain 2 at the broken chain suddenly surges, and the load shared by the original chain 1 and chain 2 will be borne entirely by chain 2. After breaking the chain, the tension of chain 2 fluctuates greatly, and the fluctuation of chain tension is larger than that of chain tension in stable operation.
Fig. 7Dynamic response of working condition at the front and rear of the chain fracture without coal body
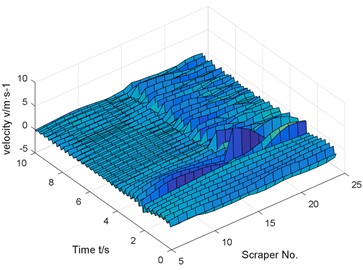
a) Vibration velocity of scraper
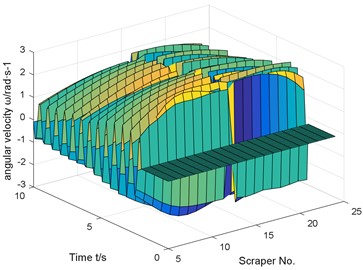
b) Scraper torsional vibration angular velocity
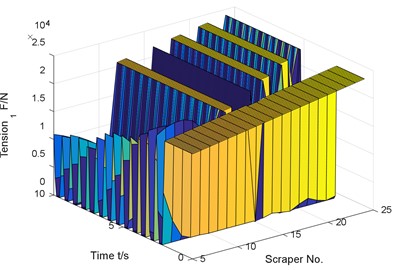
c) Tension of chain 1
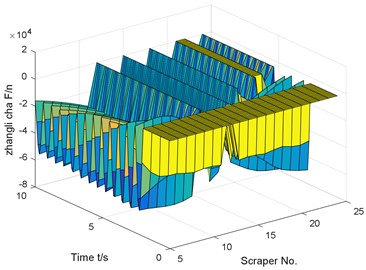
d) Tension of chain 2
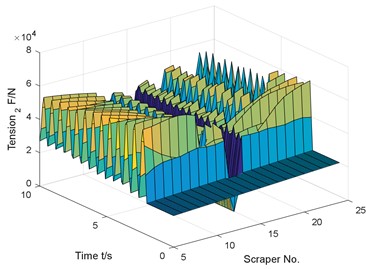
e) The tension difference between chain 1 and chain 2
4.2. Dynamic response of scraper chain system with material in front and rear
Aiming at the broken chain, under the condition that there are materials, the dynamic analysis model of the coupling of scraper torsional vibration and chain longitudinal vibration is established, as shown in Fig. 8. The simulation results are shown in Fig. 9.
Fig. 8Schematic diagram of working condition at the front and rear of the chain fracture with coal body
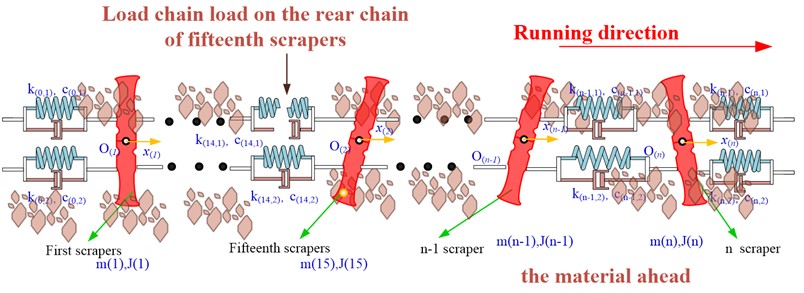
Fig. 9Response analysis results
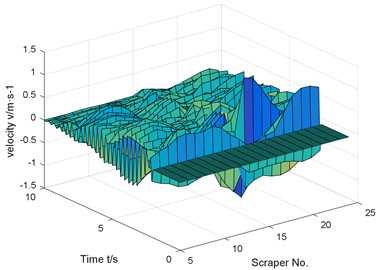
a) Vibration velocity of scraper
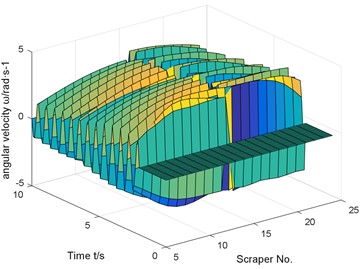
b) Scraper torsional vibration angular velocity
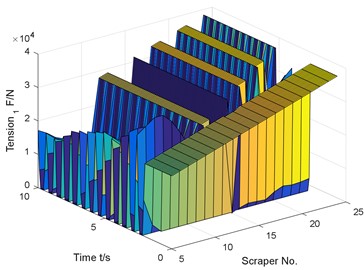
c) Tension of chain 1
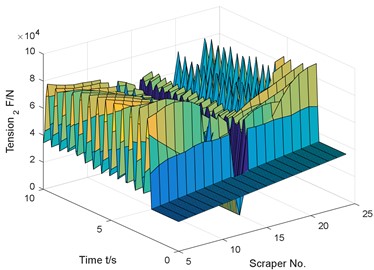
d) Tension of chain 2
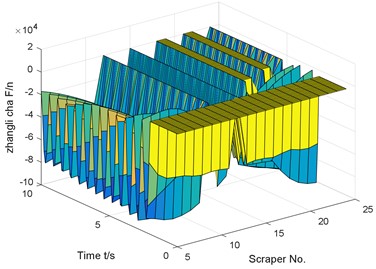
e) The tension difference between chain 1 and chain 2
The numerical results show that the sudden breaking of the chain will cause the violent fluctuation of the chain tension and the torsional pendulum vibration of the scraper. And in the case of coal in front and back of the chain break, compared with the normal operating conditions, the chain speed fluctuation reached 194.4 %.
4.3. Dynamic response of scraper chain system with material in front and no material in rear
Under the condition that there is coal at the front of the chain break, the dynamic analysis model of the coupling of scraper torsional vibration and chain longitudinal vibration is established, as shown in Fig. 10.
Fig. 10Schematic diagram of working condition at the front of the chain fracture with coal body
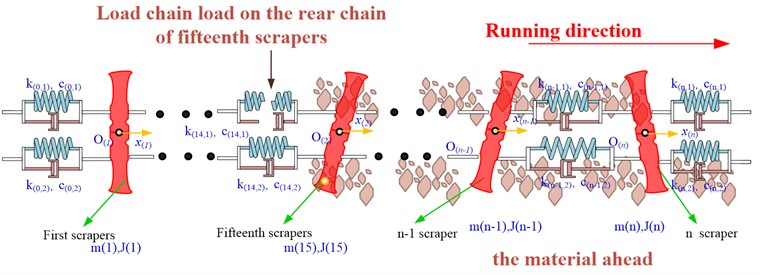
Fig. 11Response analysis results
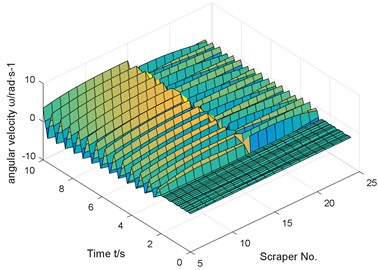
a) Vibration velocity of scraper
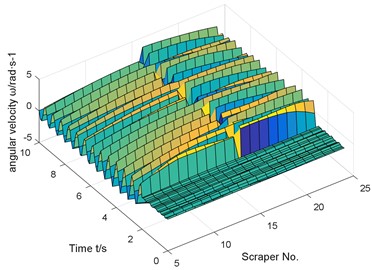
b) Scraper torsional vibration angular velocity
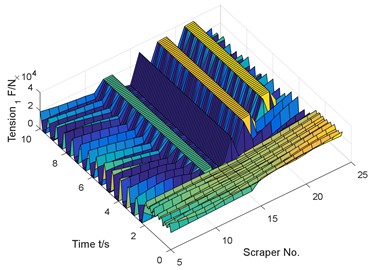
c) Tension of chain 1
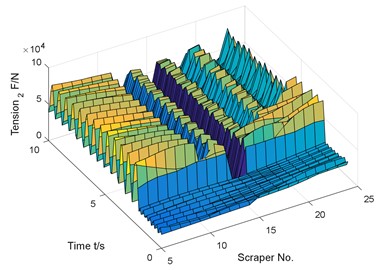
d) Tension of chain 2
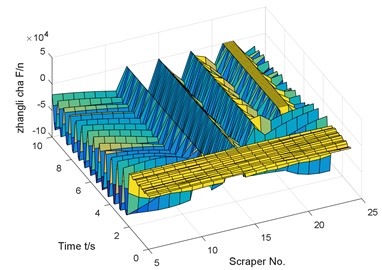
e) The tension difference between chain 1 and chain 2
In this paper, the tension of the chain on one side of the quasi-broken chain is suddenly removed, that is, the tension of the chain is zero to simulate the sudden breaking of the chain. The dynamic response characteristics of the scraper and the chain after the side chain is broken are numerically calculated by using MATLAB software. The numerical results shown in Fig. 11 are obtained.
Similar to the previous numerical results, if there is coal body in front of the chain break, but there is no coal body behind, the chain speed fluctuation reaches 310.5 % compared with the normal operating conditions.
4.4. Dynamic response of scraper chain system with no material in front and material in rear
Under the condition that there is coal at the rear of the chain break, the dynamic analysis model of the coupling of scraper torsional vibration and chain longitudinal vibration is established, as shown in Fig. 12.
Similar to the previous numerical results, if there is no coal body in front of the chain break, but there is coal body behind, the chain speed fluctuation reaches 543.1 % compared with the normal operating conditions.
Fig. 12Schematic diagram of working condition at the rear of the chain fracture with coal body
Fig. 13Response analysis results
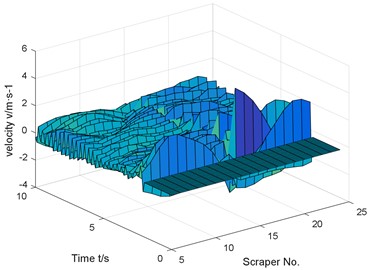
a) Vibration velocity of scraper
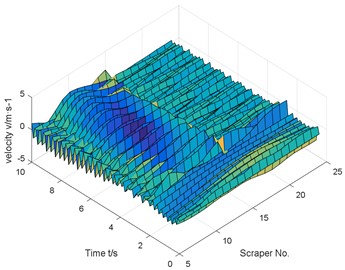
b) Scraper torsional vibration angular velocity
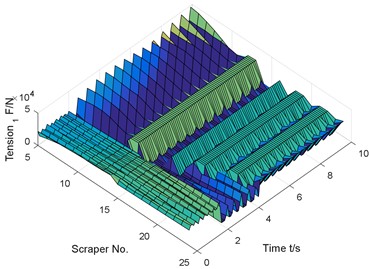
c) Tension of chain 1
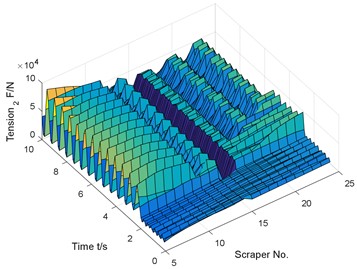
d) Tension of chain 2
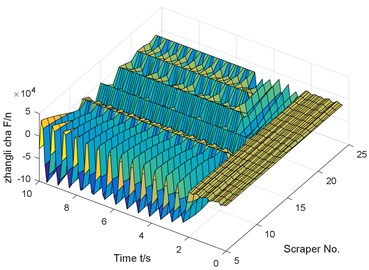
e) The tension difference between chain 1 and chain 2
5. Conclusions
In this paper, the vibration model of scraper and chain system of scraper conveyor is established. The dynamic response law of coal before and after the chain fracture under different conditions is numerically simulated and calculated.
The calculation results show that when there is material behind the broken chain, the longitudinal tension of the chain and the oscillating vibration of the scraper reach the maximum value, and the chain speed fluctuation reaches 543.1 % compared with the normal operating conditions. Only when there is material in front of the broken chain, the longitudinal tension mutation of the chain and the oscillating vibration value of the scraper are weaker than those of the previous working conditions. When there are materials at the front and back of the broken chain, the sudden change of the longitudinal tension of the chain and the oscillating vibration value of the scraper are the minimum, but they also reach twice the normal working condition, and the chain speed fluctuation reached 194.4 %. The research results of this paper provide a theoretical basis for grasping the operation status of the scraper conveyor in the coal mine and predicting the life of the scraper conveyor.
References
-
H. Tu, S. Tu, Y. Yuan, F. Wang, and Q. Bai, “Present situation of fully mechanized mining technology for steeply inclined coal seams in China,” Arabian Journal of Geosciences, Vol. 8, No. 7, pp. 4485–4494, Jul. 2015, https://doi.org/10.1007/s12517-014-1546-0
-
Z.-X. Liu, C.-X. Xie, and J. Mao, “Analysis of operation resistance of scraper conveyor based on material distribution characteristics,” Journal of China Coal Society, Vol. 43, No. 3, pp. 1155–1161, 2018, https://doi.org/10.13225/j.cnki.jccs.2017.1389
-
J. Mao, J.-N. Lu, and C.-X. Xie, Study on Dynamic Characteristics of Chain Drive System of Scraper Conveyor. (in Chinese), Emergency Management Press, 2022.
-
X. Zhang, W. Li, Z. Zhu, W. Ren, and F. Jiang, “Tension monitoring for the ring chain transmission system using an observer-based tension distribution estimation method,” Advances in Mechanical Engineering, Vol. 9, No. 9, p. 168781401772725, Sep. 2017, https://doi.org/10.1177/1687814017727251
-
S. Jiang et al., “Dynamic analysis of the scraper conveyor under abnormal operating conditions based on the vibration and speed characteristics,” Shock and Vibration, Vol. 2021, No. 2, pp. 1–17, Feb. 2021, https://doi.org/10.1155/2021/8887744
-
S. Jiang et al., “Dynamic characteristics of the chain drive system of scraper conveyor based on the speed difference,” IEEE Access, Vol. 8, No. 8, pp. 168650–168658, 2020, https://doi.org/10.1109/access.2020.3023551
-
Q. Zhang, J. Y. Gu, J. M. Liu, and Y. Tian, “Temperature effect on the impact characteristics of mine ring chain under different working conditions,” Strength of Materials, Vol. 53, No. 1, pp. 189–197, Jan. 2021, https://doi.org/10.1007/s11223-021-00275-1
-
M. Dolipski, E. Remiorz, and P. Sobota, “Dynamics of non-uniformity loads of AFC drives,” Archives of Mining Sciences, Vol. 59, No. 1, pp. 155–168, Mar. 2014, https://doi.org/10.2478/amsc-2014-0011
-
H. Wang, Q. Zhang, and F. Xie, “Dynamic tension test and intelligent coordinated control system of a heavy scraper conveyor,” IET Science, Measurement and Technology, Vol. 11, No. 7, pp. 871–877, Oct. 2017, https://doi.org/10.1049/iet-smt.2016.0425
-
R. Xia, X. Wang, B. Li, X. Wei, and Z. Yang, “The prediction of wear on a scraper conveyor chute affected by different factors based on the discrete element method,” Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 233, No. 17, pp. 6229–6239, Sep. 2019, https://doi.org/10.1177/0954406219861130
-
Z. Shi and Z. Zhu, “Case Study: wear analysis of the middle plate of a heavy-load scraper conveyor chute under a range of operating conditions,” Wear, Vol. 380-381, pp. 36–41, Jun. 2017, https://doi.org/10.1016/j.wear.2017.03.005
-
J. Duan, J. Zhou, Y. You, and X. Wang, “Time-domain analysis of vortex-induced vibration of a flexible mining riser transporting flow with various velocities and densities,” Ocean Engineering, Vol. 220, p. 108427, Jan. 2021, https://doi.org/10.1016/j.oceaneng.2020.108427
-
F. Jia, N. Deb, and G. S. Sajja, “Prediction of operation vibration state of coal mine mechatronics equipment based on data mining,” Journal of Vibroengineering, Vol. 24, No. 6, pp. 1016–1026, Sep. 2022, https://doi.org/10.21595/jve.2022.22318
-
H. Wang, D. Sun, and D. Qin, “A new continuously variable transmission system applied to transmission system of the roadheader’s cutting unit,” Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 231, No. 19, pp. 3590–3600, Oct. 2017, https://doi.org/10.1177/0954406216649404
-
Z.-X. Liu, C.-X. Xie, J. Mao, and M. Xie, “Analysis of Longitudinal and Torsional Pendulum Coupling Vibration of Scraper Conveyor Under Material Loading Condition,” Zhendong Ceshi Yu Zhenduan Journal of Vibration, Vol. 39, No. 1, pp. 147–152, 2019, https://doi.org/10.16450/j.cnki.issn.1004-6801.2019.01.022
About this article
The authors are grateful to the support from the Liaoning Provincial Department of Education Project (LJ2020QNL012) and Liaoning Province Applied basic Research Program Project (Youth Project 2023JH2/101600061).
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
Chunxue Xie: method. Zhixiang Liu: data. Miao Xie: simulation.
The authors declare that they have no conflict of interest.
