Dynamic response analysis of bearing-rotor system considering cage whirling motion

Hong, Jie; Zhang, Jian; Wang, Yongfeng; Ma, Yanhong; Cheng, Ronghui

doi:10.21595/vp.2022.22803

Vibroengineering Procedia

Browse Procedia

Published: 25 August 2022

Check for updates

Dynamic response analysis of bearing-rotor system considering cage whirling motion

Jie Hong¹

Jian Zhang²

Yongfeng Wang³

Yanhong Ma⁴

Ronghui Cheng⁵

^{1, 2, 4}Research Institute of Aero-Engine, Beihang University, Beijing, China

³School of Energy and Power Engineering, Beihang University, Beijing, China

⁵AECC Shenyang Engine Research Institute, Shenyang, China

Corresponding Author:

Yongfeng Wang

Cite the article Download PDF

Downloads 339

CrossRef Citations 2

Abstract

Dynamic model of bearing-rotor system is developed considering the collision effects between the cage and its guiding land. The modal characteristic and vibration response are studied with the fourth-order Runge-Kutta method. It is demonstrated that the cage whirling motion arising as a result of collision with the guiding land would induce abnormal frequency components in the system’s response including the multiple frequency as well as the modulation between the speed frequency and the natural frequency. Additionally, cage whirling motion and rotor vibration become severe when the rotor rotates around its pitching-mode critical speed. It is shown that the amplitudes of abnormal frequencies can be decreased by reducing rotor unbalance in a given range.

1. Introduction

Rolling bearing is widely used in rotating machinery, and its performance directly affects the rotor dynamic response. Bearing cage is significant component to separate and guide elements. Cage whirling motion due to destructive collision force between the cage and rolling elements or race land can give rise to destruction of bearing structure and abnormal vibration of rotor system. Fig. 1 shows one typical case of bearing structure failure, and cage spin frequency $f_{c}$ modulated to rotor rotation frequency $f_{0}$ , producing sideband signals $f_{0}$ ± $f_{c}$ , which might generate great harm to the security of whole equipment. Therefore, it is critical to study the mechanism of cage whirling motion and its influence on the dynamic characteristic of bearing-rotor system.

Fig. 1Typical case of bearing damage and rotor vibration problem related to cage whirling motion

a) Cage fracture and element wearing

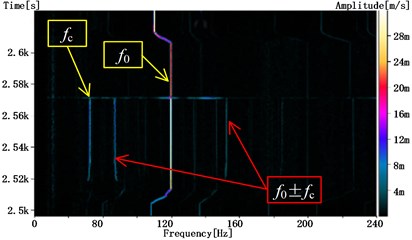
b) Frequency modulation in rotor vibration signal

In the past decades, many researches have been conducted about the dynamic characteristic of bearing cage. Kingsbury [1] firstly put forward the mechanism that the amplitude of cage whirling motion would varies at a particular frequency because of element loading inequality and periodically changing sides within their pockets. Walters [2] numerically integrated the bearing motion equations with a fourth order Runge-Kutta scheme, and the results demonstrated that the cage whirling direction would be different as the cage guiding condition was changed. After that, abundant works have been done about dynamic modeling, parameters effects and motion stability of bearing cages [3]-[6]. However, the influence of rotor dynamic response on the cage motion are hardly considered. On the other hand, dynamic analysis of bearing-rotor system is the hotspot in rotating machinery engineering, but the scholars are mainly focused on the nonlinear stiffness and rotor instability caused by bearing clearance or varying compliance [7]-[9], ignoring the effect of cage motion or excitation. In recent years, some studies on the dynamic interaction between bearing cage and rotor system have been conducted. Chen [10] investigated the effects of rotor vibration on the cage dynamic performance. But the mechanism of cage whirling motion and its influence on the rotor dynamic remains unclear.

In this paper, a dynamic model for high-speed bearing-rotor system considering cage whirling motion and the cage collision with its guiding land is proposed. On the basis, the cage motion characteristic and the frequency components of the rotor response are studied in order to investigate the dynamic coupling effects between rotor and bearing cage.

2. Dynamic model of bearing-rotor system

The structure of typical bearing-rotor system supported by fulcrums is shown in Fig. 2. $k_{i}$ , $c_{i}$ , $l_{i}$ ( $i =$ 1, 2) are respectively supporting stiffness, damping coefficient and distance to the centroid of two fulcrums. In order to simplify the question, only the effect the rear bearing is investigated, as shown in Fig. 3, and the interface of inner ring and rotor journal is considered totally bounded.

Fig. 2Structural sketch of typical bearing-rotor system

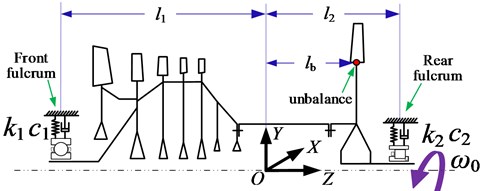
Fig. 3Structural diagram of the rolling bearing at the rear fulcrum

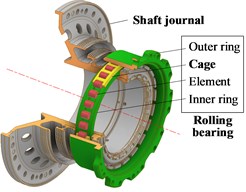
2.1. Dynamic differential equations of the rotor system

Assuming the rotor is rigid, the dynamic equations of the rotor system are written in Eq. (1):

1

\begin{array}{l} \begin{array}{l} m_{0} {\ddot{x}}_{0} + k_{1} (x_{0} + l_{1} θ_{X}) + c_{1} ({\dot{x}}_{0} + l_{1} {\dot{θ}}_{X}) = m_{e 0} e_{0} ω_{0}^{2} \cos ω_{0} t + Q_{2 x}, \\ m_{0} {\ddot{y}}_{0} + k_{1} (y_{0} - k_{1} θ_{Y}) + c_{1} ({\dot{x}}_{0} - l_{1} {\dot{θ}}_{Y}) = m_{e 0} e_{0} ω_{0}^{2} \sin ω_{0} t + Q_{2 y}, \end{array} \\ \begin{array}{l} I_{d} {\ddot{θ}}_{X} - I_{p} ω_{1} {\dot{θ}}_{Y} + l_{1} k_{1} (y_{0} - l_{1} θ_{X}) + l_{1} k_{1} ({\dot{y}}_{0} - l_{1} {\dot{θ}}_{X}) = l_{b} m_{e 0} e_{0} ω_{0}^{2} \cos ω_{0} t - l_{2} Q_{2 x}, \\ I_{d} {\ddot{θ}}_{Y} + I_{p} ω_{1} {\dot{θ}}_{X} + l_{1} k_{1} (x_{0} + l_{1} θ_{Y}) + l_{1} k_{1} ({\dot{x}}_{0} + l_{1} {\dot{θ}}_{Y}) = l_{b} m_{e 0} e_{0} ω_{0}^{2} \sin ω_{0} t - l_{2} Q_{2 y}, \end{array} \end{array}

where $m_{0}$ , $I_{d}$ , $I_{p}$ are respectively the rotor’s mass, polar and diameter moment of inertia; $m_{e 0}$ , $e_{0}$ are the rotor unbalance and its eccentricity, which is considered located at the rear half; $l_{b}$ is the distance between the centroid to the unbalance; $ω_{0}$ is the angular velocity; $Q_{2 x}$ , $Q_{2 y}$ are bearing force components in $X$ and $Y$ direction at the rear fulcrum.

2.2. Bearing forces considering cage collision with guiding land

Plenty of researches have been conducted to describe the bearing forces $Q_{2 x}$ and $Q_{2 y}$ in Eq. (1). Based on the bearing dynamic model developed in [11] and [12], this article further considers the effects of cage whirling motion and cage collision with its guiding land. The forces acting on cage are shown in Fig. 4, and the dynamic differential equations of cage are established as Eq. (2).

In Eq. (2), $N$ is the number of elements; $m_{c}$ is the mass of cage; $I_{c}$ represents moment inertias of cage on different directions; $ψ_{c}$ and $φ_{c}$ are the skewing angular and position angles; $F_{c}^{j c n}$ , $F_{c}^{j c t}$ are respectively the contact forces between cage and element in normal and tangential directions; $M_{c}^{j c n}$ , $M_{c}^{j c t}$ are torques due to the cage skewing and the force maldistribution. $M_{c o}^{i}$ , $M_{c o}^{o}$ are respectively the lubricating oil resistances:

2

\{\begin{array}{l} \begin{array}{l} m_{c} {\ddot{x}}_{c} = \sum_{j = 1}^{N} (F_{c}^{j c n} \sin φ_{j} + F_{c}^{j c t} \cos φ_{j}) + F_{c}^{g n} \cos φ_{c}^{g} + F_{c}^{g t} \sin φ_{c}^{g} + F_{c}^{r} \cos φ_{c}^{b}, \\ m_{c} {\ddot{y}}_{c} = \sum_{j = 1}^{N} (F_{c}^{j c n} \cos φ_{j} - F_{c}^{j c t} \sin φ_{j}) + F_{c}^{g n} \sin φ_{c} - F_{c}^{g t} \cos φ_{c} + F_{c}^{r} \sin φ_{c}^{b}, \end{array} \\ I_{c}^{Z} {\ddot{φ}}_{c}^{b} = \sum_{j = 1}^{N} (F_{c}^{j c n} d_{m} / 2) - M_{c o}^{i} - M_{c o}^{o}, I_{c}^{X} {\ddot{ψ}}_{c}^{X} = \sum_{j = 1}^{N} (M_{c}^{j c t} \sin φ_{j} - M_{c}^{j c n} \cos φ_{j}), \\ I_{c}^{Y} {\ddot{ψ}}_{c}^{Y} = \sum_{j = 1}^{N} (M_{c}^{j c n} \sin φ_{j} + M_{c}^{j c t} \cos φ_{j}) . \end{array}

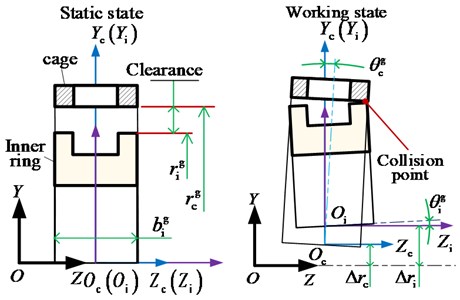
As shown in Fig. 5, there is an initial clearance ( $c_{0}^{g}$ ) between the cage and its guiding land at static state, and the clearance varies ( $c_{w}^{g}$ ) during the working process due to the skewing and procession motion of the cage and inner ring, which is expressed as Eq. (3):

3

c_{w}^{g} = c_{0}^{g} - [Δ r_{i} - Δ r_{c} + r_{i}^{g} (1 - \cos θ_{i}^{g}) + b_{g} \sin θ_{i}^{g} - r_{c}^{g} (1 - \cos θ_{c}^{g}) + b_{g} \sin θ_{c}^{g}],

where $r_{i}^{g}$ , $r_{c}^{g}$ are respectively the radius of cage and inner ring at the guiding area; $b_{g}$ is the half width of the guiding land in $Z$ direction. $Δ r$ , $θ^{g}$ are the procession radius and skewing angle.

The collision between cage and inner ring occurs when $c_{w}^{g} \leq 0$ . The normal and tangential component of the collision force respectively are:

4

F_{c}^{g n} = k_{c}^{g n} \cdot a b s (c_{w}^{g}), F_{c}^{g t} = μ_{c}^{g n} F_{c}^{g n},

where $k_{c}^{g n}$ is the stiffness characteristic of the cage-land contact, and $μ_{c}^{g n}$ is the friction coefficient.

Fig. 4Schematic diagram of the forces acting on the cage

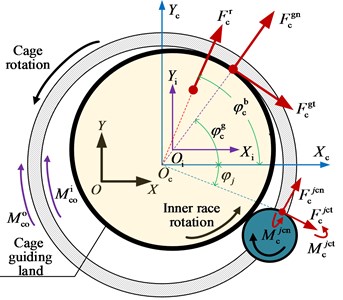
Fig. 5Schematic diagram of the collision effect between the cage and its guiding land

The dynamic model of the whole bearing-rotor system consists of the rotor model part (Eq. (1)) and the bearing model part, including the bearing forces model (Eq. (2)). These two parts are assembled with the equilibriums of the inner ring, which is fixed on and keeps the same displacement with the rotor shaft. The force balance equations for the inner ring are:

5

\{\begin{array}{l} Q_{2 x} - \sum_{j = 1}^{N} (F_{j}^{o n} \cos φ_{j} + F_{j}^{o t} \sin φ_{j}) - (F_{c}^{g t} \sin φ_{c}^{g} + F_{c}^{r} \cos φ_{c}^{b}) = 0, \\ Q_{2 y} - \sum_{j = 1}^{N} (F_{j}^{o n} \sin φ_{j} - F_{j}^{o t} \cos φ_{j}) - (F_{c}^{g t} \cos φ_{c} - F_{c}^{r} \sin φ_{c}^{b}) = 0, \end{array}

where $F_{j}^{o n}$ , $F_{j}^{o t}$ are respectively the normal and tangential force between the element and the outer raceway, and $M_{j}^{o n}$ , $M_{j}^{o t}$ are torques due to the element skewing and the force maldistribution.

2.3. Calculation procedure of the dynamic model

The basic steps of the calculation procedure for dynamic equations of the whole bearing-rotor system are listed as follow:

1) Input the structural parameters and working conditions (including rotation speed, preload) of the system, and start the quasi-static analysis with Newton-Raphson method to acquire the initial displacement/velocity state.

2) Calculate the interaction forces/toques on the basis of the dynamic models, and acquire the acceleration state of the whole system.

3 Conduct time integration calculation by the four order Runge-Kutta method. Reduce the time increment if the truncation error exceeds the allowance. Otherwise, update the displacement/velocity state for the next timestep until the time ending.

3. Results and discussion

Based on the above dynamic model and calculation method, modal characteristics and dynamic response of the bearing-rotor system is analyzed considering the effect of cage whirling motion. The key parameters of the system are shown in Table 1.

Table 1Structural parameters of the bearing-rotor system

Rotor parameters
Rotor mass $m_{0}$	200 kg	Centroid distance to unbalance $l_{b}$	300 mm
Rotor diameter rotary inertia $I_{p}$	20 kg∙m²	Rotor unbalance $m_{e 0}$	100 g
Unbalance eccentricity $e_{0}$	10 mm	Centroid distance to unbalance $l_{b}$	300 mm
Front supporting stiffness $k_{1}$	2.5e7 Nm	Rear supporting stiffness $k_{2}$	4e7 Nm
Centroid distance to front fulcrums $l_{1}$	600 mm	Centroid distance to rear fulcrums $l_{2}$	450 mm
Bearing parameters
Number of the elements	16	Radial internal clearance	0.04 m $m$
Cage mass $m_{c}$	0.2704 kg	Cage unbalance	10 g∙mm
Cage pocket clearance	0.1 mm	Cage guiding clearance $c_{0}^{g}$	0.04 mm

3.1. Modal characteristics of the simple supported rotor system

Eigenvalue of Eq. (1) is obtained given $m_{e 0}$ equals to zero, and modal characteristics of the simple supported rotor system are analyzed. Campbell diagram and mode diagrams under the critical speed of the rotor system are shown in Fig. 6 and Fig. 7 respectively. The first order of the rotor modal is translational mode whose critical speed is 5400 rpm, and the second order is pitching mode whose critical speed is 10711 rpm.

3.2. Dynamic response of the bearing-rotor system

On the basis of modal characteristics analysis, four typical speeds are picked up including 2 krpm, 5 krpm, 10 krpm and 20 krpm, corresponding four typical rotating states: far below the critical speed, near to the translational critical speed, near to the pitching critical speed and far above the critical speed. Fig. 8 shows the dynamic responses of the bearing-rotor system under these four typical speeds.

Fig. 6Campbell diagram of the simple supported rotor system

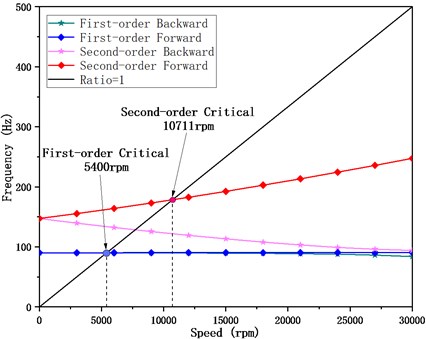
Fig. 7Mode diagrams of the simple supported rotor system under critical speeds

a) The first order, translational mode

b) The second order, pitching mode

Fig. 8Dynamic responses of the bearing-rotor system under different speed

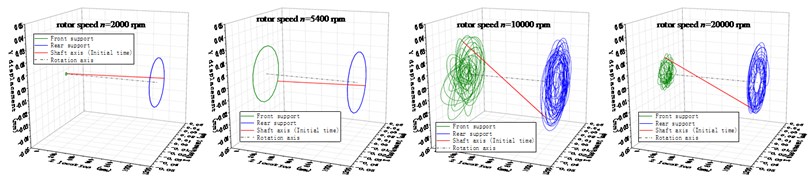
a) Center orbits at the fulcrums and the shaft axis of the rotor

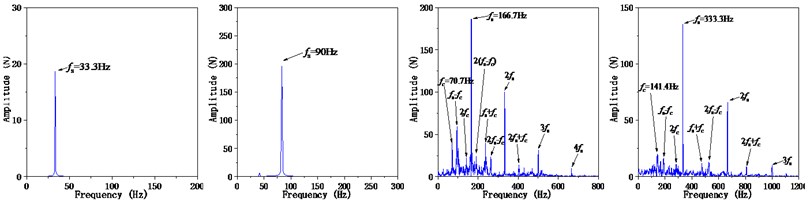
b) Frequency spectrums of the rear fulcrum load response

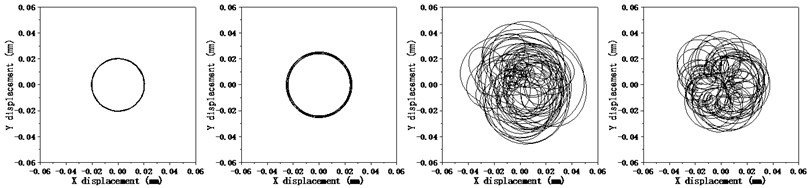
c) Center orbit of the cage

The results show that the rotor rotates under the translational mode shape at 2 krpm and 5 krpm, and rotating speed frequency is the only component in the spectrums of fulcrum load response. The cage center orbits are both circular with a similar radius. However, the load response of the rear fulcrum is higher at the 5 krpm as the rotor system is near to the resonance range.

The pitching mode shape of the rotor system is observed at the speed of 10 krpm and 20 krpm, and the frequency components are much more complicate, including the rotor rotatory speed $f_{s}$ , the cage rotatory speed $f_{c}$ , and their multiple frequencies ${2 f}_{s}$ , ${2 f}_{c}$ , $3 f_{s}$ , $3 f_{c}$ … and the modulation frequencies, for example, $f_{s} \pm f_{c}$ , $2 f_{s} \pm f_{c}$ and so on. The cage center orbits no longer keep circular, and there are severe collisions between the cage and its guiding land, leading to the cage whirling motion. The results exhibit the coupling effects between the rotor and the bearing cage when the rotor is rotating under the pitching mode.

3.3. Effects of the rotor unbalance on the dynamic response

Additional conditions of different rotor unbalance (20 g, 200 g) are considered and the dynamic responses of the bearing-rotor system are analyzed, as shown in Fig. 9. The rotor pitching angle and the rear fulcrum load response both increase when adding the rotor unbalance. However, the amplitudes at the modulation frequencies are found to be lower than the 100 g unbalance condition. When the rotor unbalance is 20 g, the response of whole system is at a lower level, and the collision of the cage is weaker. When it comes to the 200 g condition, rotor’s centrifugal effect is too strong, and the cage is forced to whirling on the rotor’s orbit, which also leading to the reduction of the cage collision effect and the components of modulation frequencies in the response signal.

Fig. 9Effects of the rotor unbalance on the dynamic response of the system

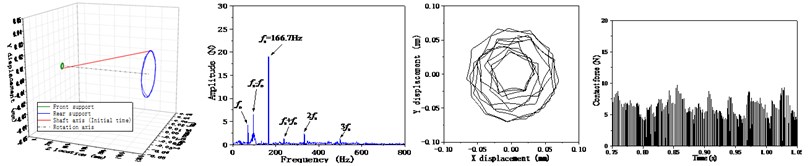
a) Rotor unbalance = 20 g

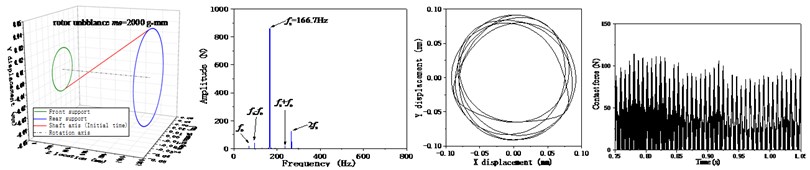
b) Rotor unbalance = 200 g

4. Conclusions

Through the analysis, the conclusions can be drawn as follow:

1) The influence of the cage whirling motion should be considered during the dynamic response analysis of the bearing-rotor system, which can cause abnormal vibration of the rotor system, inducing the multiple frequencies and modulation frequencies components in the system response.

2) The cage whirling motion is more easily induced when the rotor rotates around its pitching mode critical speed, as the skewing of the shaft and the inner ring exacerbates the collision between the cage and its guiding land.

3) The abnormal vibration of the bearing-rotor system can be suppressed by controlling the rotor unbalance, which essentially decreases the shaft pitching angle and the cage-guiding land collision effects.

References

E. P. Kingsbury, “Torque variations in instrument ball bearings,” ASLE Transactions, Vol. 8, No. 4, pp. 435–441, Jan. 1965, https://doi.org/10.1080/05698196508972113

Publisher
C. T. Walters, “The dynamics of ball bearings,” Journal of Lubrication Technology, Vol. 93, No. 1, pp. 1–10, Jan. 1971, https://doi.org/10.1115/1.3451516

Publisher
C. R. Meeks and K. O. Ng, “The dynamics of ball separators in ball bearings-part i: analysis,” ASLE Transactions, Vol. 28, No. 3, pp. 277–287, Jan. 1985, https://doi.org/10.1080/05698198508981622

Publisher
C. R. Meeks, “The dynamics of ball separators in ball bearings-part II: results of optimization study,” ASLE Transactions, Vol. 28, No. 3, pp. 288–295, Jan. 1985, https://doi.org/10.1080/05698198508981623

Publisher
B. Choe, W. Kwak, D. Jeon, and Y. Lee, “Experimental study on dynamic behavior of ball bearing cage in cryogenic environments, Part Ⅱ: Effects of cage mass imbalance,” Mechanical Systems and Signal Processing, Vol. 116, No. 1, pp. 25–39, Feb. 2019, https://doi.org/10.1016/j.ymssp.2018.06.034

Publisher
W. Liu, X. Zhang, S. Wang, Y. Zhang, and G. Wang, “Application of cage guided by combined action of outer race and balls in beating vibration reduction,” Journal of Vibration and Shock, Vol. 39, No. 21, pp. 24–33, 2020, https://doi.org/10.13465/j.cnki.jvs.2020.21.004

Publisher
T. Yamamoto, “On critical speeds induced by ball bearings at lower rotating speeds,” Bulletin of JSME, Vol. 1, No. 3, pp. 240–244, 1958, https://doi.org/10.1299/jsme1958.1.240

Publisher
C. S. Sunnersjö, “Rolling bearing vibrations: the effects of varying compliance, manufacturing tolerances and wear,” Aston University, 1976.

Search CrossRef
Y. Ma, T. He, D. Zhang, and J. Hong, “Imbalance response of rotor system with nonlinear bearing stiffness,” Journal of Aerospace Power, Vol. 29, No. 7, pp. 1528–1534, 2014, https://doi.org/10.13224/j.cnki.jasp.2014.07.003

Publisher
S. Chen, R. Wang, X. Chen, J. Gu, and Z. Liu, “Analysis of dynamic coupling characteristics of high speed angular contact ball bearing-rigid rotor system under different working conditions,” Journal of Aerospace Power, Vol. 37, No. 2, pp. 344–355, 2022, https://doi.org/10.13224/j.cnki.jasp.20210082

Publisher
S. Deng, Q. Jia, and J. Xue, Design Theory of Rolling Bearing. Beijing: Standards Press of China, 2014.

Search CrossRef
Y. Cui, S. Deng, H. Yang, W. Zhang, and R. Niu, “Effect of cage dynamic unbalance on the cage’s dynamic characteristics in high-speed cylindrical roller bearings,” Industrial Lubrication and Tribology, Vol. 71, No. 10, pp. 1125–1135, Dec. 2019, https://doi.org/10.1108/ilt-12-2018-0462

Publisher

Cited by

Nonlinear dynamics of full-ceramic bearing-rotor system considering structural defects in cage pockets

Zhan Wang | Xuhui Liang | Zinan Wang | Yang Liu | Ye Zhang

(2024)

Failure analysis of an aero-engine inter-shaft bearing due to clearance between the outer ring and its housing

Zhefu Yang | Jie Hong | Dong Wang | Yanhong Ma | Ronghui Cheng

(2023)

About this article

Received

11 July 2022

Accepted

10 August 2022

Published

25 August 2022

SUBJECTS

Fault diagnosis based on vibration signal analysis

DOI

https://doi.org/10.21595/vp.2022.22803

Keywords

bearing-rotor system

cage whirling motion

dynamic response

frequency modulation

Acknowledgements

The research was funded by the National Natural Science Foundation of China (Grant No. 52075018) and National Science and Technology Major Project (Grant No. 2017-IV-0011-0048).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2020 10 19

Study on response characteristics of rotor-bearing system under sudden base excitation load

Zhaojun Feng, Guihuo Luo, Zedong Yang, Nan Zheng, Wei Chen

Research article

2018 08 15

Dynamic response analysis for the aero-engine dual-rotor-bearing system with flexible coupling misalignment faults

Zhenyong Lu, Xiaodong Wang, Lei Hou, Yushu Chen, Hongliang Li

Research article

2017 09 30

Experimental investigations on effects of axial clearance on high-speed turbine expansion generator rotor response

Dongjiang Han, Jinfu Yang, Zhengwei Wang

Research article

2017 02 15

Nonlinear dynamics study of a high-temperature rotor-bearing-seal system in gas turbine

Rui Zhu, Yanru Zhang, Jianxing Ren, Hongguang Li, Qingkai Han

J. Hong, J. Zhang, Y. Wang, Y. Ma, and R. Cheng, “Dynamic response analysis of bearing-rotor system considering cage whirling motion,” Vibroengineering PROCEDIA, Vol. 44, pp. 21–27, Aug. 2022, https://doi.org/10.21595/vp.2022.22803

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2022.22803
UR  - https://doi.org/10.21595/vp.2022.22803
TI  - Dynamic response analysis of bearing-rotor system considering cage whirling motion
T2  - Vibroengineering PROCEDIA
AU  - Hong, Jie
AU  - Zhang, Jian
AU  - Wang, Yongfeng
AU  - Ma, Yanhong
AU  - Cheng, Ronghui
PY  - 2022
DA  - 2022/08/25
PB  - JVE International Ltd.
SP  - 21-27
VL  - 44
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Hong_2022,
	doi = {10.21595/vp.2022.22803},
	url = {https://doi.org/10.21595/vp.2022.22803},
	year = 2022,
	month = {aug},
	publisher = {{JVE} International Ltd.},
	volume = {44},
	pages = {21--27},
	author = {Jie Hong and Jian Zhang and Yongfeng Wang and Yanhong Ma and Ronghui Cheng},
	title = {Dynamic response analysis of bearing-rotor system considering cage whirling motion},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]J. Hong, J. Zhang, Y. Wang, Y. Ma, and R. Cheng, “Dynamic response analysis of bearing-rotor system considering cage whirling motion,” Vibroengineering PROCEDIA, vol. 44, pp. 21–27, Aug. 2022, doi: 10.21595/vp.2022.22803.

Copy IEEE

Copied to clipboard!

Hong, Jie, Jian Zhang, Yongfeng Wang, Yanhong Ma, and Ronghui Cheng. “Dynamic Response Analysis of Bearing-Rotor System Considering Cage Whirling Motion.” Vibroengineering PROCEDIA 44 (August 25, 2022): 21–27. https://doi.org/10.21595/vp.2022.22803.

Copy Chicago

Copied to clipboard!

Dynamic response analysis of bearing-rotor system considering cage whirling motion

Abstract

1. Introduction

2. Dynamic model of bearing-rotor system

2.1. Dynamic differential equations of the rotor system

2.2. Bearing forces considering cage collision with guiding land

2.3. Calculation procedure of the dynamic model

3. Results and discussion

3.1. Modal characteristics of the simple supported rotor system

3.2. Dynamic response of the bearing-rotor system

3.3. Effects of the rotor unbalance on the dynamic response

4. Conclusions

References

Cited by

About this article

Related Articles