Abstract
The quay crane is a special mechanical equipment which can lift the container vertically and horizontally through intermittent circulation movement. Fatigue crack is one of the main kinds of damage in quay cranes. The generation and development of fatigue crack are invisible, which makes the identification of fatigue cracks a great challenge. From the dynamic point of view, fatigue cracks have nonlinear dynamic characteristics beyond the linear dynamic category. The traditional damage detection methods based on linear hypothesis are difficult to effectively recognize the nonlinear dynamic characteristics of fatigue cracks, so they cannot be effectively used for structural fatigue crack detection. In order to overcome the limitations of the existing linear damage detection methods, bispectrum analysis, a nonlinear dynamic analysis method, is introduced in this thesis. By drawing on the use of bispectrum analysis to describe the nonlinear dynamic characteristics of rotating structures, a fatigue crack detection method based on nonlinear dynamic characteristics of quay cranes is developed.
1. Introduction
Quay Cranes are in a very important and unique position in the increasingly fierce international trade and port competition. Quay Cranes are typical welded metal structures. In addition, when the quay crane is working, the trolley is constantly started and braked, or the suspended load is shuttling between the front and rear main beams at high speed, resulting in alternating stress in the structure and causing dislocation movement accumulation and fatigue cracks. However, the current main health monitoring methods of quay cranes are still based on the visual inspection of experienced personnel and magnetic particle inspection, which obviously cannot meet the huge demand of quay cranes [1].
The Korean scholar Hyawn [2] studied the stress change of the quay cranes under the wind load, and demonstrated that even a very small wind load will cause the stress on the safety device of the quay cranes to increase rapidly, which is related to the increase rate of the wind load. Jacobs [3] evaluated and characterized the critical elastic response and derailment vibration response of portal frame of large quay cranes under earthquake load through the shaking table test of a 1:20-scaling quay crane model. Vöth [4] focused on the safety problems of the quay cranes caused by the high-speed operation of the trolley. Most of the existing studies focus on the safety assessment and reliability research of quay cranes under special loads, especially the earthquake loads. The damage detection of quay cranes under long-term service conditions is rarely considered. The special load will cause great damage to quay cranes, but it is worth noting that on the one hand, the occurrence of the special load is very accidental, and it is very likely that a quay crane will not be affected by such special loads as earthquake loads during the whole service period. On the other hand, most of the faults and damages of quay cranes are caused by long-time and high-speed operation during daily service. Therefore, while paying attention to the damage of the structure caused by special loads, it is also necessary to develop a structural damage detection method based on long-term and daily monitoring data processing of the quay cranes.
2. Bispectrum analysis method
It is assumed that the mean value of real random signal is zero and -order is stationary. If the -order cumulant of exists, the -order spectrum is defined as the ()-dimensional Fourier transform of :
When 3, the third-order spectrum is also called bispectrum, expressed in .
The estimated bispectrum[5-6]can be expressed as:
where is the Fourier transform determined by the sequence of principal values of ; means complex conjugate.
and in are two mutually independent frequencies, which can represent non minimum phase information. is a double periodic function with the same period. The period is 2, and satisfies:
There are six symmetry lines which are , , , , and in . Since the bispectrum satisfies such high symmetry, all the bispectrum can pass through the symmetric region , , .
3. The finite element simulation
In this paper, an 80 t-65 m quay crane is taken as the prototype to build the finite element model. The relevant parameters are shown in Table 1. The material of the quay crane is Q345 steel, and the material property is: elastic modulus 2.06×1011 Pa, Poisson's ratio = 0.3, density = 7.85×103 kg/m3. In this paper, the quay crane is set in the working state, that is, the crane is completely locked and in the windless environment. Therefore, the front girder can be regarded as a complex cantilever beam model, and fixed constraints will be set at the bolt holes on the land side. This is to simplify the model and calculation.
Table 1Main parameters of the model
Front extension (m) | Back extension (m) | Crane gauge (m) | Trolley gauge (m) | Base distance (m) | Load capacity (t) | |
65 | 30.5 | 35 | 6.3 | 20.5 | Sling | Cliver |
65 | 80 | |||||
A 50 %- degree breathing crack is set at five positions as shown in Fig. 1. respectively. A simple harmonic excitation is set on the upper surface of the free end near the sea side. 50000 N, ( 0.353 Hz is the first-order natural frequency of the front girder with a breathing crack). The acceleration response of the structure is extracted at the lower surface of the free end near the sea side, and bispectrum analysis is performed. The results are shown in Fig. 2.
When the breathing crack transits from the fixed end near the land side to the free end near the sea side, the second harmonic in the bispectrum gradually changes from obvious to not obvious, but the amplitude of the second harmonic is the smallest in the middle section of the front girder; When the crack is close to the fixed end on the land side and the free end on the sea side, the amplitude of the second harmonic is larger. However, it should be noted that this change rule is not invariable, and may generally change due to the difference between the position where the excitation is applied and the position where the dynamic response is extracted.
Fig. 1Diagram of damage position on the front girder of the quay bridge

Fig. 2Three-dimensional bispectrum when the damage is at different position
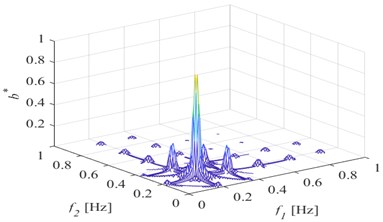
a) Position 1
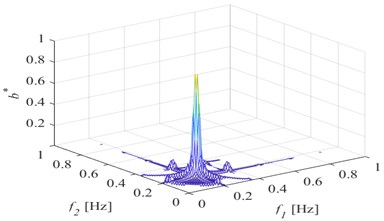
b) Position 2
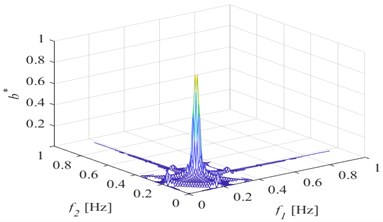
c) Position 3
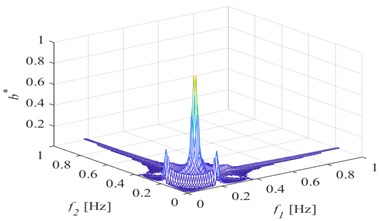
d) Position 4
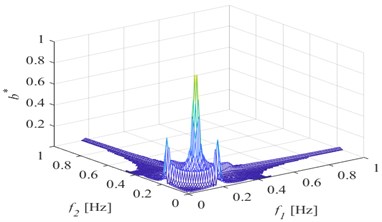
e) Position 5
A breathing crack is set at position 1 near the fixed end, and the crack depth is set as 10 %, 20 %, 30 %, 40 %, and 50 %, respectively to study the change of the bispectral nonlinear dynamic characteristics under different damage degrees. A simple harmonic excitation is set on the upper surface of the free end near the sea side, where the excitation size is set to 50 000 N and the excitation frequency is set to . The acceleration response of the structure is extracted at the lower surface of the free end near the sea side, and bispectrum analysis is performed. The results are shown in Fig. 3.
Fig. 3Bispectrum when a) p= 10 %; b) p= 20 %; c) p= 30 %; d) p= 40 %; e) p= 50 %
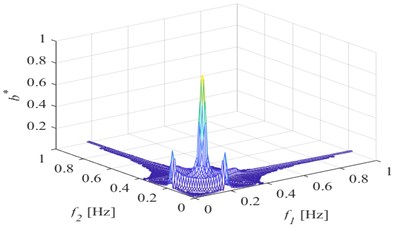
a)10 %
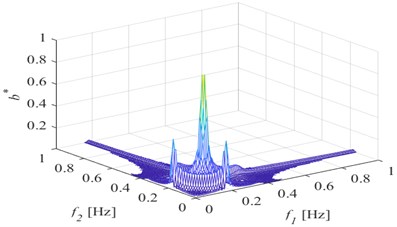
b)20 %
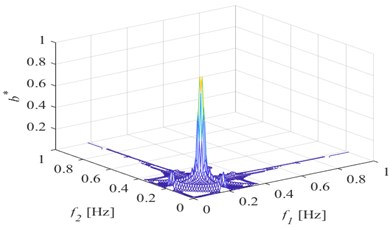
c)30 %
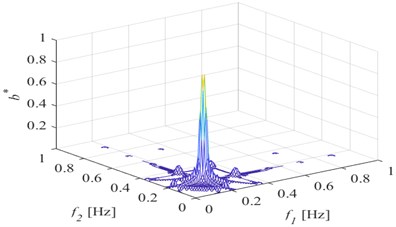
d)40 %
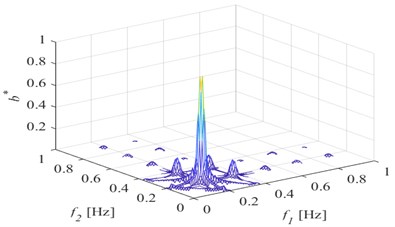
e) 50 %
Fig. 4Variation trend of the second harmonic amplitude with crack depth
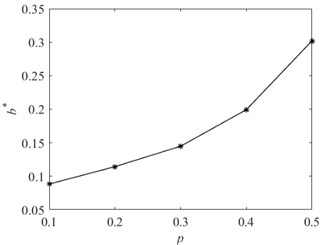
Fig. 3 shows that the second harmonic component of the bispectrum becomes more and more obvious with the deepening of the damage degree, and the amplitude is also larger and larger. Among them, when the damage degree is 10 % and 20 %, the second harmonic component can be observed, but it is not obvious compared with the case of 50 % damage depth, which may be related to the monitoring position and normalization processing method. Extract the second harmonic amplitude under different crack depths, and the change is shown in Fig. 4. It can be seen from the figure that the amplitude of the second harmonic of the bispectrum monotonically increases with the crack depth. Therefore, the second harmonic component of the bispectrum can be used as a characteristic index to identify the fatigue damage degree.
4. Conclusions
In this paper, the bispectrum dynamic analysis is carried out on the quay crane which is under working condition. The results show that bispectrum analysis can extract the nonlinear dynamic characteristics of the crane structure with fatigue cracks. The bispectral nonlinear dynamic characteristics are positively correlated with the depth of fatigue crack in the structure. The bispectral nonlinear dynamic characteristics no longer show a single change law with the change of crack position. The research results show that the proposed fatigue crack detection method based on bispectrum analysis can capture the nonlinear dynamic characteristics of fatigue cracks in the structure of quay cranes under different working conditions, and provides a new technology for fatigue crack identification of quay cranes. It must be noted that, bispectrum analysis method has shown unprecedented advantages in the fault detection of structure components, especially rotating components, but it is rarely used in the damage detection of large and complex structures. Therefore, this paper only proposes new possibilities for the fatigue crack detection of quay cranes. However, if this method is really to be used in the actual structure monitoring, it must be further studied.
References
-
W. Pei, K. Q. Ding, and D. J. Wu, “Method of Safety Health Monitoring and Damage Alarming for Cranes,” Mechanical Engineering and Automation, Vol. 6, pp. 120–122, 2010, https://doi.org/10.3969/j.issn.1672-6413.2010.06.045
-
K. D. Hyawn, O. B. Cheol, and C. I. Sik, “Effect of wind velocity variation on Safety factor of container crane tie-downs,” KSCE Journal of Civil and Environmental Engineering Research, Vol. 25, No. 6A, pp. 1127–1131, 2005.
-
L. D. Jacobs, B. D. Kosbab, R. T. Leon, and R. Desroches, “Seismic behavior of a jumbo container crane including uplift,” Earthquake Spectra, Vol. 27, No. 3, pp. 745–773, Aug. 2011, https://doi.org/10.1193/1.3610238
-
S. Vöth, “Safety concepts for container crane hoists,” in Proceedings of the 17th ITI-Symposium, pp. 127–133, 2014.
-
P. K. Ajmera, N. S. Nehe, D. V. Jadhav, and R. S. Holambe, “Robust feature extraction from spectrum estimated using bispectrum for speaker recognition,” International Journal of Speech Technology, Vol. 15, No. 3, pp. 433–440, Sep. 2012, https://doi.org/10.1007/s10772-012-9153-5
-
M. S. Cao, Y. M. Xu, K. Q. Ding, and E. Manoach, “Bispectral dynamics features for characterizing structural fatigue damage,” Journal of Vibroengineering, Vol. 20, No. 5, pp. 2073–2084, Aug. 2018, https://doi.org/10.21595/jve.2018.19963
About this article
This work is supported by Anhui provincial international joint research center of data diagnosis and smart maintenance on bridge structures (No. 2021AHGHYB05), the University scientific research project of Anhui Provincial Department of Education (Nos. KJ2021A1097 and KJ2021A1098), the Key R&D Project of Anhui Science and Technology Department (202004b11020026), and Nanjing International Joint Research and Development Program (No. 202112003).
