Abstract
In order to accurately simulate structural fatigue crack damage, the non-linear contact model was selected and verified to be suitable for the fatigue crack simulation in cantilever beam. The influence of damage severity and location on harmonic vibration responses were revealed. Moreover, the damage identification indexes based on harmonic excitation response were constructed, and the effectiveness used to identify fatigue crack damage was validated. The results reveal that contact model is effective in simulating fatigue crack and sensitive to nonlinear fatigue crack through the comparative analysis of harmonic vibration response of intact structure and damaged one. For the vibration responses of beam with different damage severities and locations, the greater the damage severity is, and the closer the damage location is to the fixed end, the more obvious the non-linear vibration characteristics presents. Two damage indicators including distortion value of phase spectrum () and proportion of super/sub-harmonic amplitudes () are applied, which can effectively characterize the change of fatigue crack with different damage location and severity. Furthermore, contact model presents stronger non-linear information compared with bilinear model, which is more suitable for fatigue damage simulation.
Highlights
- The suitable model for nonlinear fatigue crack simulation is determined.
- The influence of damage condition on harmonic vibration responses is revealed.
- The damage identification indexes for fatigue crack are constructed and validated.
1. Introduction
Structural health monitoring (SHM) system plays an important role in ensuring bridge structural safety. Damage identification as an important part of SHM is sensitive to structural stiffness reduction [1]. The development of damage diagnosis and data mining theory further promotes the accuracy of structural damage identification [2-4]. However, structural damage usually manifests in the appearance of cracks, and gradually undergoes a process from less to more, from small to large. Fatigue cracks exist as a great menace to engineering structures, because they are barely visible and hard to detect. Actual structure cracks under external loads and environments present contact-closure breathing phenomenon, which is typical non-linear fatigue damage [5]. The difference between local stiffness reduction and fatigue crack damage is significant in structural damage identification. Traditional damage identification method based on global dynamic characteristics fails to identify the fatigue crack damage [6]. In recent years many studies have been dedicated to analyzing the dynamic behavior of cracked structures, and aim to develop an effective method for crack detection based on structural vibrations. Fatigue damages can reduce the structural stiffness, which change their mechanical behaviors. Therefore, sensitive damage identification method for fatigue cracks is essential to evaluate fatigue crack and ensure the safe operation of structure [7, 8].
Traditional damage identification methods assumed that the crack is open during vibration. Rucevskis et al. [9] realized the identification of damaged beams simulated through mill-cut using modal shape curvature squares. He et al. [10] proposed a two-phase damage identification method for beam structure based on wavelet signal processing by considering moving load. Damages of beam were introduced by saw cut. Cui et al. [11] proposed a damage identification method for beam structure with single and multi-damage cases under different degrees and locations of damage based on strain modes and operational modal analysis, where cracks were introduced by high-precision electric tools. Kopsaftopoulos et al. [12] simulated the local stiffness reduction by adding mass blocks at the structural joints to simulate the damage effect. Cao et al. [13] constructed bilateral milling grooves to simulate the local damage of Euler Bernoulli beam, and defined size parameters to characterize the damage degree. Perera et al. [14] used the reduction of bending stiffness to simulate damage and realized damage identification through numerical simulation. These methods did not consider the nonlinear effect of fatigue crack, which lead to the inappropriate conclusions.
A fatigue crack that periodically opens and closes subject to a harmonic excitation can be referred to as a breathing crack. Some researchers have investigated the damage identification of actual fatigue cracks [15, 16]. Benedetti et al. [17] presented a frequency-shift-based damage identification method for reinforced concrete beam with fatigue cracks. Prawin et al. [18] presented a baseline-free method to realize the detection and localization of breathing cracks using singular spectrum analysis. Smith et al. [19] developed a Bayesian approach for fatigue crack identification using nonlinear forced responses considering uncertainty effects. Andreaus et al. [20-22] conducted experimental and numerical researches about nonlinear forced response of cantilever beam with fatigue cracks. Wimarshana et al. [23] realized the breathing crack detection of cantilever beam using entropy method, which could identity the early crack damage of 3% beam thickness. Zhang et al. [24] modeled the fatigue crack as two elastic, frictionless half space and investigated the threshold behaviors of subharmonic responses. The results revealed that the subharmonic component could be used to identify the fatigue crack of structure. Panigrahi and Pohit [25] investigated a time domain nonlinear modeling of cracked functionally graded Timoshenko beam. An exhaustive parametric study on effects of cracks, material properties, multi frequency excitation, influence of super harmonics on periodic as well as quasi periodic nonlinear dynamic response of thick and thin beams were performed. Xu et al. [26] proposed a novel concept of nonlinear pseudo-force (NPF) for crack identification, and the capability of NPF in detecting and locating breathing cracks was verified on beams with breathing cracks. Kharazan et al [27] investigated the nonlinear vibration behavior of a cantilever beam with multiple breathing cracks. They analyzed and verified the sensitivity of the beam’s nonlinear response to the different number of breathing cracks and various crack depths. The superior sensitivity of higher order harmonics embodied in guided ultrasonic waves has been broadly exploited, to develop high-precision nondestructive evaluation and structural health monitoring techniques [28, 29]. Xu et al. [30] developed a new theoretical model based on the elastodynamic reciprocity theorem, and gained insight into the generation of second harmonics in Lamb waves. By virtue of the model, a nonlinear damage indicator, governed by the quantified second harmonic generated by the crack, was defined, to calibrate crack severity quantitatively. Basu et al. [31] investigated a relatively new nonlinear ultrasonic technique, namely the sideband peak count-index (or SPC-I), which provided the highest sensitivity to the damage progression and could be effectively used as a very robust nonlinear ultrasonic tool for identifying the crack damage. Currents research results revealed that nonlinear characteristics of the forced vibration responses of structure with fatigue crack must be considered in damage identification. More efforts need to be conducted to demonstrate the effect of damage severity and location on harmonic response of cracked structure. Damage indicators suitable for fatigue crack identification need to be proposed and verified.
In this study, a cantilever beam was adopted as numerical object. Fatigue crack was simulated through contact model. The influences of excitation frequency, damage severity and damage location on harmonic vibration responses of beam were investigated. Damage indicators based on phase spectrum and Fourier spectrum were constructed and evaluated. Furthermore, harmonic response of cracked beam simulated through contact model and bilinear model were compared.
2. Theoretical model and methods
2.1. Cracked cantilever beam
Cantilever beam produced by Q345 steel with left end fixed was adopted as research object . Its physical properties are length 0.3 m, section dimension 0.02 m×0.02 m, Young’s modulus of elasticity 206.8 GPa, Poisson’s ratio 0.3 and mass density 7850 kg/m3. The distance between crack location and fixed end is , and the depth of crack damage is , which were shown in Fig. 1(a). The relative crack position can be expressed by , and the relative damage severity can be expressed by . The finite element model of cantilever beam was established using two-dimensional plane element PLANE 182. The grids near crack were refined, which was shown in Fig. 1(b). Modal properties of cracked cantilever beam will change with the location and depth of crack. Through finite element analysis, modal frequency of fatigue cracked cantilever beam with different crack depths (0.1, 0.2, 0.3, 0.4, 0.5) and locations (0.07, 0.27, 0.47, 0.67) can be calculated, which is used for determining the frequency of harmonic excitation.
Fig. 1Cantilever beam model with fatigue crack

a) Model parameters

b) Refined grids near crack
2.2. Modelling of breathing crack
2.2.1. Contact model
Contact modelling is a highly nonlinear method, which can be used to simulate the fatigue crack process. Contact models are divided into frictional contact model and non-frictional one. When there is friction contact, the friction coefficient . Slipping occurs along the contact surface when the tangential force reaches a certain degree. At this time, the tangential force is related to the loading path, and the change process is irreversible. When there is no friction contact, the friction coefficient , tangential force and loading path are independent, and the change process is reversible. The results have shown that the friction between crack surfaces presented little influence on dynamic response. Therefore, the friction-free contact model is used to simulate fatigue cracks in this study.
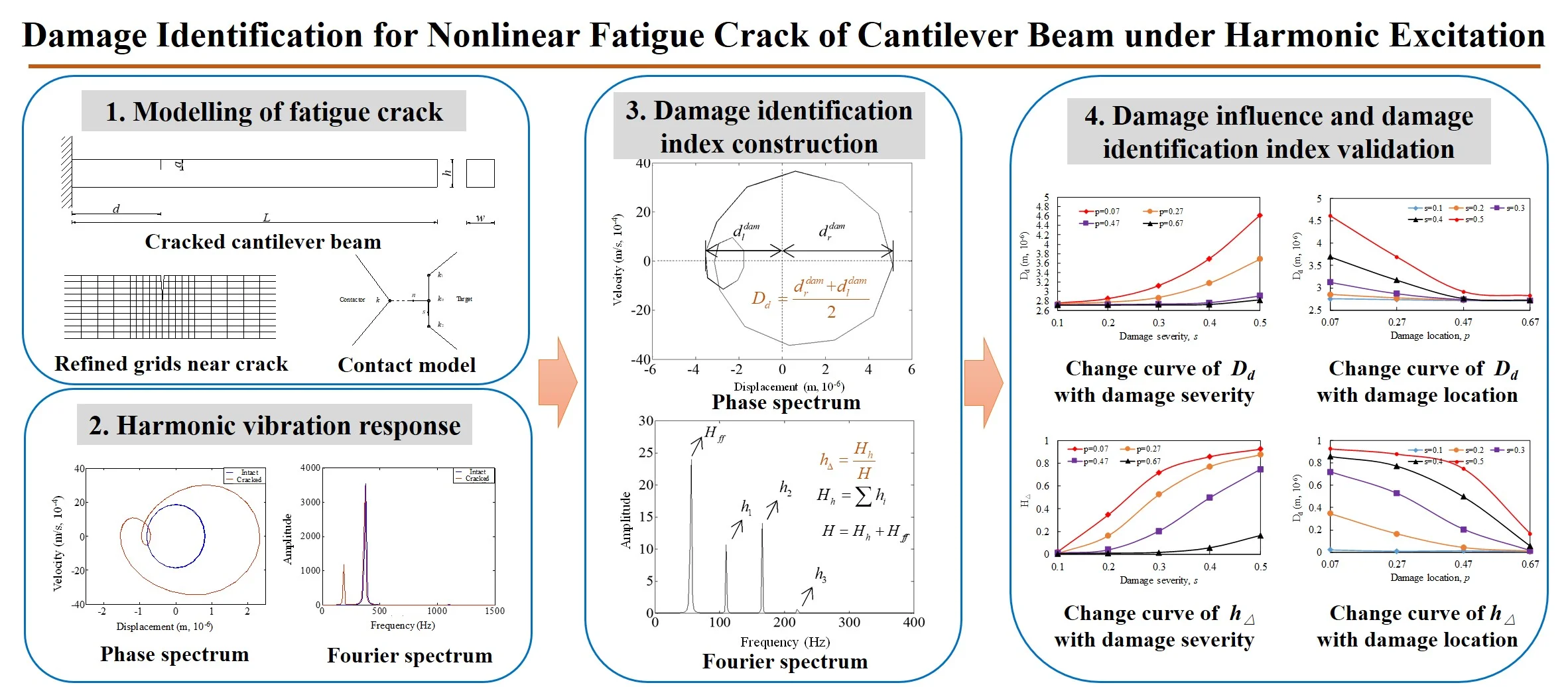
The calculation methods of surface-to-surface contact include penalty function method and extended Lagrange multiplier method. Compared with penalty function method, the stiffness matrix is not easy to be ill-conditioned when using extended Lagrange multiplier method, and the setting of contact stiffness is more reasonable. The contact surface is composed of contactor surface and target surface. According to the contact conditions, the contactor elements cannot penetrate the target surface, but the target elements can penetrate the contactor surface during convergence solution. In the non-friction contact problem, there are three states between the contact node and the target element: (1) there is no contact between them, and the crack is in the open state; (2) there is complete contact between them, and the crack is in the closed state; (3) in the transitional stage between the first two states, the crack is neither fully opened nor fully contacted. Therefore, the non-linear effect of contact element can be simulated through establishing contact pairs at the crack location, as shown in Fig. 2. It can be used to characterize the phenomenon that the stiffness of structure with fatigue crack always changes.
Fig. 2Nonlinear contact model
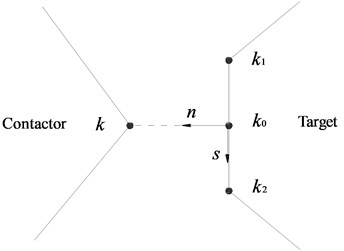
2.2.2. Bilinear model
Comparative analysis of harmonic response for cracked cantilever beam was conducted between contact model and bilinear model. When the bilinear model is used to simulate the fatigue crack, it can be considered that there are only two states for fatigue crack: opening and closure. Bilinear model of crack was shown in Fig. 3. Structural stiffnesses changes in opening stiffness and closure stiffness . When , the crack surface was in open state, and the stiffness of structure was consistent with ; When , the crack surface was in closure state, and the stiffness of structure was consistent with .
Fig. 3Bilinear model of fatigue crack
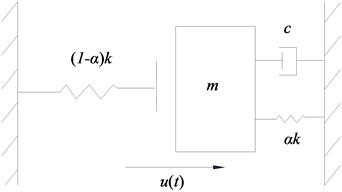
a) Bilinear spring element model
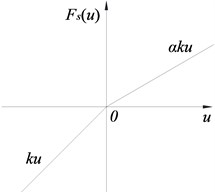
b) Diagram of bilinear stiffness change
2.3. Damage indicators of breathing crack
2.3.1. Phase spectrum-based damage indicator
Phase spectrum will produce a certain degree of distortion when the damage occurs. The more serious the damage is, the more obvious the distortion presents. The distortion value of phase spectrum is proposed as damage indicator according to the change of the spectrum along the displacement direction, which was expressed in Eq. (1) and illustrated in Fig. 4:
where, is distortion value of phase spectrum; is the maximum positive displacement of damaged beam in phase spectrum; is the maximum negative displacement of damaged beam in phase spectrum. When beam is intact, .
2.3.2. Fourier spectrum-based damage indicator
When a damaged structure is subjected to non-linear vibration, the spectrum energy of the structure is no longer concentrated at the excitation frequency. Moreover, it generates a certain degree of super/sub-harmonic components. The magnitude of the harmonic component is positively correlated with the damage degree. The amplitude energy at the excitation frequency alters when the damage degree changes. Assuming is the sum of amplitude energy of all generated super/sub-harmonic components, and is the sum of energy in all frequency domains including amplitude energy at excitation frequency. and can be calculated by:
where is the amplitude of th super/sub-harmonic component, is the amplitude at excitation frequency. and was expressed in Fig. 5.
Fig. 4Index value in phase spectrum
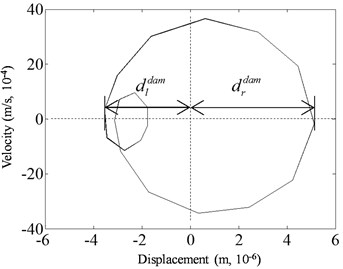
Fig. 5Index value in Fourier spectrum
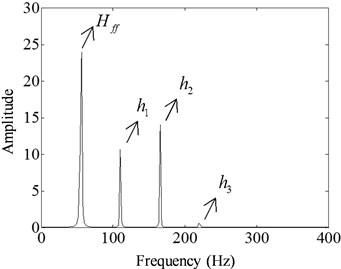
Since the occurrences and magnitudes of super/sub-harmonic components are obviously correlated with the structural damage severity. Super/sub-harmonic amplitudes ratio was proposed as damage indicator, which can be expressed by:
where, represents the proportion of super/sub-harmonic amplitudes in the total Fourier-spectrum energy due to the breathing effect of fatigue crack. When beam is intact, .
3. Results and discussions
3.1. Natural frequency of cracked cantilever beam
The first order natural frequency of cantilever beams with non-linear fatigue crack at different damage depths 0.1, 0.2, 0.3, 0.4,0.5) and locations 0.07, 0.27, 0.47, 0.67) were obtained, which are listed in Fig. 6. It can be observed that natural frequency of cantilever beam with same crack location decreases with the increase of damage severity. Moreover, the closer the crack is to the fixed end, the greater the influence on the frequency presents. The obtained natural frequencies were used to determine the harmonic excitation frequencies of beam under different crack conditions.
3.2. Harmonic vibration response of cantilever beam with fatigue crack
3.2.1. Effect of excitation frequency
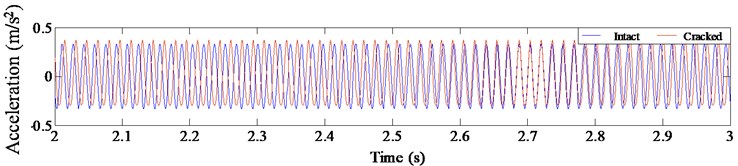
In order to investigate that the influence of nonlinear fatigue crack on harmonic vibration response of the beam, acceleration time history, phase spectrum and Fourier spectrum of the intact structure and damaged one ( 0.07, 0.2) under harmonic excitation with three frequencies ( 1/3, 1/2, 2, excitation frequency / natural frequency) are calculated, as shown in Figs. 7-9.
Fig. 6Natural frequency of cracked cantilever beam
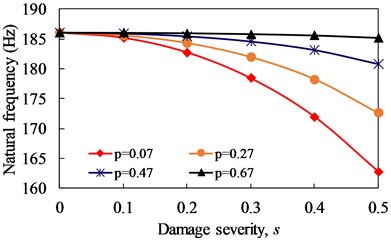
Fig. 7Harmonic vibration response for intact and cracked beam with η= 1/3
a) Acceleration time history
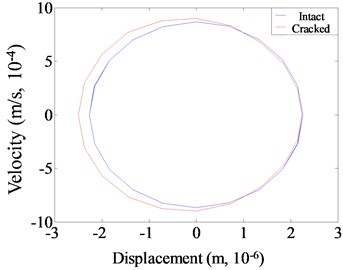
b) Phase spectrum
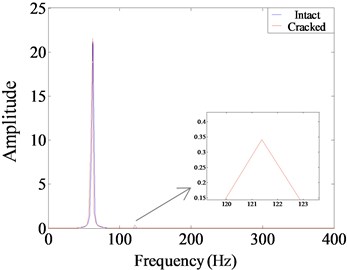
c) Fourier spectrum
As observed from Figs. 7-9, fatigue damage makes acceleration time history of cantilever beam oscillate and distort. The central axis of acceleration curve shifts, and the sawtooth shape appears at the edge of the curve. For the phase spectrum, the displacement-velocity curve of the intact structure presents a standard elliptical shape, while the curve is deformed, drifted and expanded when the structure is damaged with fatigue crack. Meanwhile, there are small irregular grooves and subsidence circles. The degree of distortion under different excitation frequencies is different. For Fourier spectrum, the most obvious non-linear characteristic is that the spectrum energy is no longer concentrated in the excitation frequency, and energy redistribution occurs. The harmonic components occur at the positions of the integer or one-fold integer times of excitation frequency. The super-harmonic component is generated at resonance of 1/3 and 1/2, while the sub-harmonic component is generated at 2.
Fig. 8Harmonic vibration response for intact and cracked beam with η= 1/2
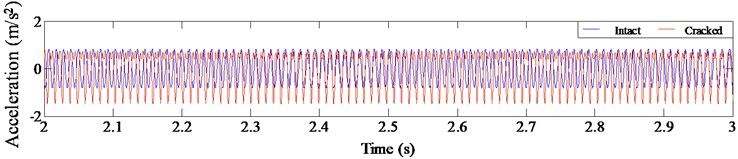
a) Acceleration time history
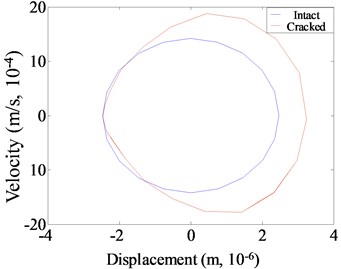
b) Phase spectrum
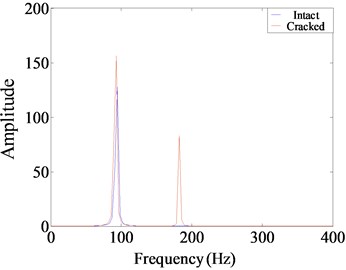
c) Fourier spectrum
Fig. 9Harmonic vibration response for intact and cracked beam with η= 2
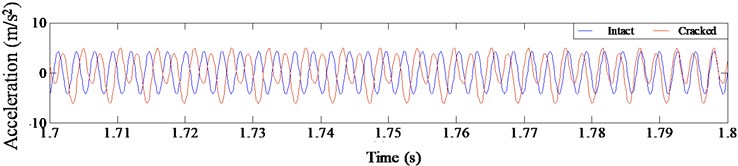
a) Acceleration time history
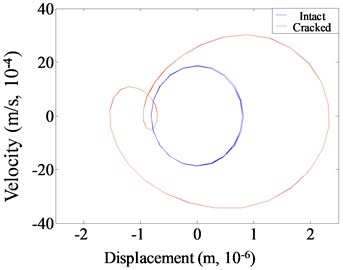
b) Phase spectrum
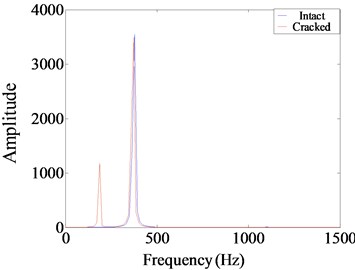
c) Fourier spectrum
3.2.2. Effect of damage severity
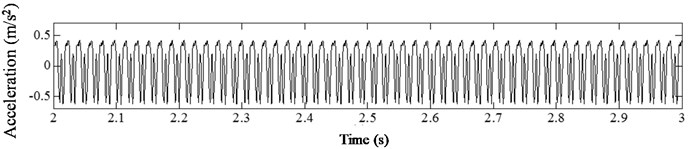
In analyzing the influence of damage severity on the harmonic vibration response of cantilever beam, different damage severities ( 0.1, 0.2, 0.3, 0.4, 0.5) were considered. Fig. 10 presents the acceleration time history curve of cantilever beam with different crack depths under harmonic loading with 1/3. As observed from the results, the curve presents migration phenomenon, and the degree of acceleration oscillation increases slightly with the increasing of damage severity when the crack occurs at the same location. Meanwhile, the sawtooth shape distortions begin to appear at the lower edge of the curve at 0.3. The sawtooth shape distortion appears slightly at the upper edge of the curve at 0.4. At 0.5, the sawtooth shape distortions of the upper and lower edges of the curve were all obvious. The same trends were also found for other conditions (0.27, 0.47, 0.67, 1/2, 2). This phenomenon can reflect the non-linear vibration characteristics of beam with fatigue crack. The greater the damage severity, the more obvious the nonlinear vibration characteristics. Therefore, the degree of distortion in acceleration time history curve can be used to characterize the effect of damage severity on vibration response of structures with fatigue cracks.
Fig. 10Acceleration time history of cracked beam with different damage severity at p= 0.07, η= 1/3
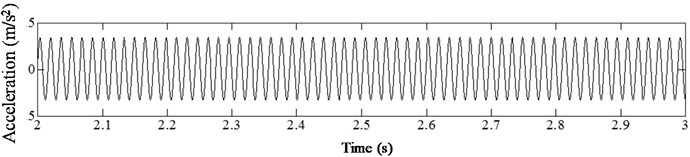
a)
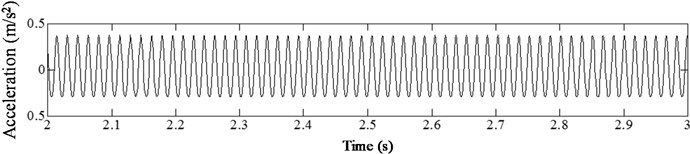
b)
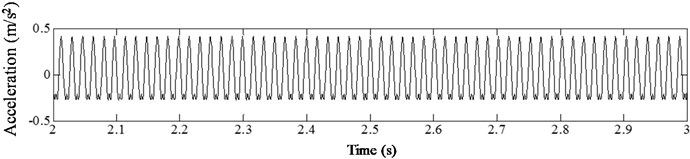
c)
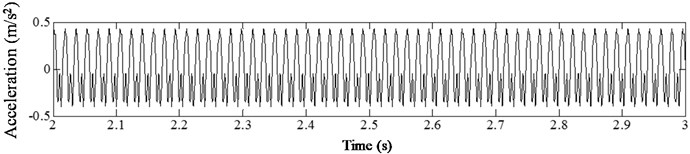
d)
e)
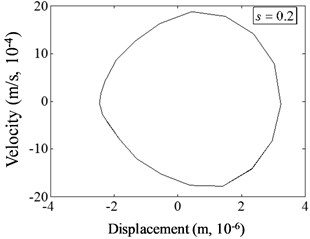
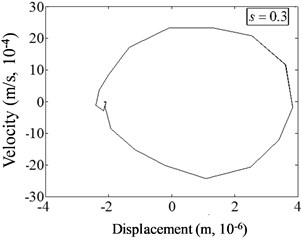
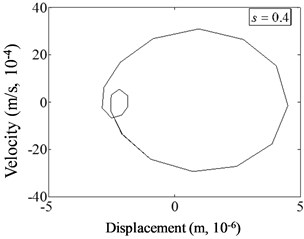
For the effect of damage severity on phase spectrum of cracked beam, Fig. 11 presents the variations of displacement versus velocity under different damage severities (0.2, 0.3, 0.4, 0.5) at 0.07 and 1/2. As observed from this figure, phase spectrum curves no longer keep the regular ellipse shapes after the structure is damaged.
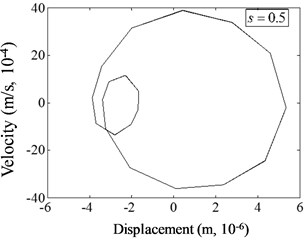
Fig. 11Phase spectrum of cracked beam with different damage severity at p=0.07, η= 1/3
a)
b)
c)
d)
Fig. 12Fourier spectrum of cracked beam with different damage severity at p=0.27, η=2
a)
b)
c)
d)
The centers of circles shift to the positive direction of displacement, and the curves distort. The displacement-velocity distribution domain increases. The deeper the damage depth is, the more obvious the non-linear phenomenon presents. When the damage severity is 0.3, a small groove appears in the curve; when 0.4, the groove evolves into an irregular shape of a small circle; when 0.5, the area of the small circle obviously enlarges. The change phenomena were also applied for other cases. Therefore, the change of damage depth has a great influence on the harmonic vibration characteristics of non-linear damaged structures. The more serious the damage is, the more significant the phase spectrum distortion is.
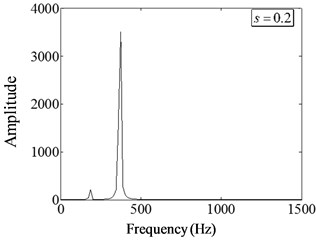
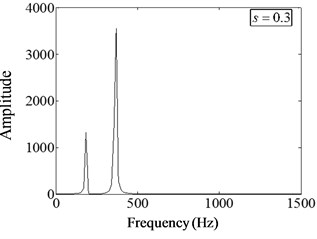
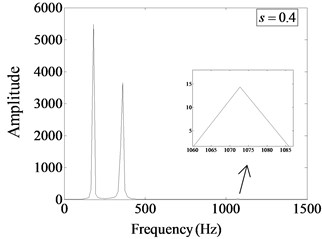
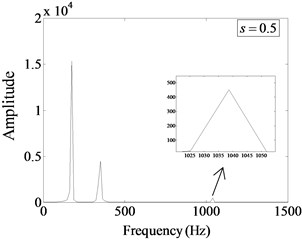
Fig. 12 shows the Fourier spectrum of beam under different damage severity (0.2, 0.3, 0.4, 0.5) at , . It can be seen that there are obvious sub-harmonic components at half of the excitation frequency. When the damage severity is small, the magnitude of subharmonic component is weak compared with the amplitude of excitation frequency. When the damage severity increases, the magnitude of subharmonic component increases correspondingly, and becomes much larger than the corresponding magnitude of excitation frequency. When the damage severity is large enough (, ), a certain degree of super-harmonic component appears at its integer multiple of the excitation frequency. These phenomena show that the magnitude of sub-harmonic component is the main characteristic of power spectrum under high frequency harmonic excitation, and these characteristics are enough to characterize the influence of damage severity on the harmonic response characteristics of non-linear fatigue cracked beams. the more serious the damage is, the greater the impact exhibits.
3.2.3. Effect of damage location
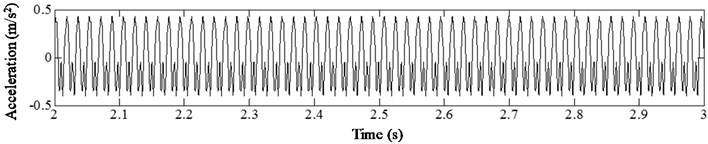
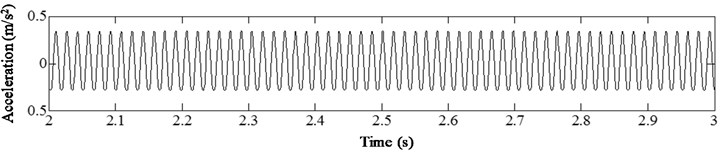
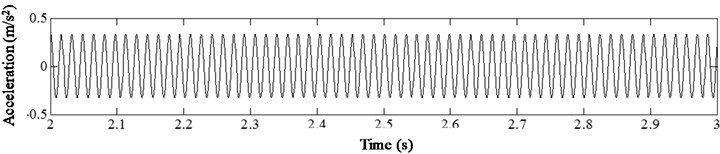
To demonstrate the influence of damage location on harmonic vibration response of non-linear cracked structures, crack locations 0.07, 0.27, 0.47, 0.67 were considered. Fig. 13 shows the acceleration time history curve of different crack positions under harmonic excitation frequency 1/3 and relative damage severity .
Fig. 13Acceleration time history of cracked beam with different damage locations at s=0.4, η= 1/3
a)

b)
c)
d)
It can be observed from the results that when the damage location is near the fixed end (), the curve contains obvious sawtooth distortion, and there is unequal distribution at both ends of the acceleration zero line. With the crack away from the fixed end, the sawtooth shape in the curve gradually weakens, and the unequal distribution of the curve is no longer obvious. Therefore, the influence of crack location on the structural vibration response can be reflected by the acceleration time-history signal curve for a cantilever beam with fatigue crack. When the crack is near the fixed end, its non-linear characteristics are obvious. When the crack is away from the fixed end, its non-linear characteristics are weakened.
Fig. 14 illustrates the phase spectra of different crack locations under harmonic excitation of relative excitation frequency 1/2 and damage severity . It can be concluded that the shape of the curve in the phase spectrum changes with crack position. When the crack is near the fixed end ( 0.07), the phenomenon of curve distortion and migration is the most obvious. Irregular small circles are sunk inward, and the displacement value of the curve is the largest. When the position of the crack changes to the free end, the phenomenon of curve distortion and migration is weakened, and the irregular small circles gradually become smaller () until disappear ( 0.47, 0.67). And the displacement value of the curve also decreases. It can be found from phase spectrum that the changes of fatigue crack location cause the variation of the harmonic vibration characteristics of cracked beam. The more near to the fixed end the damage is, the more obvious the distortion of phase spectrum exhibits.
Fig. 14Phase spectrum of cracked beam with different damage locations at s=0.4, η= 1/2
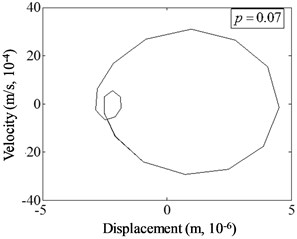
a)
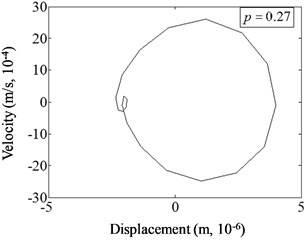
b)
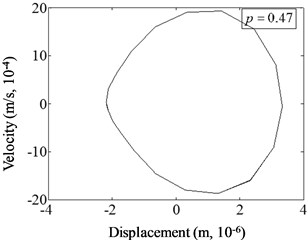
c)
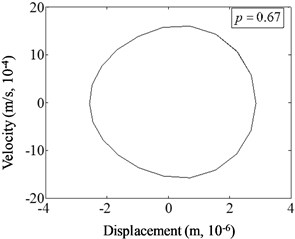
d)
Fig. 15 shows the Fourier spectrum of cracked beam at different crack locations when the relative damage degree and the relative frequency of harmonic excitation 1/2. The analysis shows that when the crack is near the fixed end (), the excited super-harmonic order is more. Corresponding amplitude of the first harmonic component is relatively larger, which occupies the main position in the total amplitude energy. When the crack is away from the fixed end and close to the free end, the amplitude of the harmonic component decreases gradually, and the second-order harmonic amplitude nearly disappears. When the position of the crack changes, the amplitude of the first harmonic component is less than the amplitude of the excitation frequency, which indicates that the non-linear effect of the structure caused by the fatigue crack is weak. Therefore, the farther the crack is from the fixed end, the smaller the impact of fatigue crack on the vibration response of the structure presents.
Fig. 15Fourier spectrum of cracked beam with different damage locations at s=0.5, η= 1/2
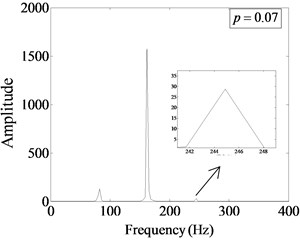
a)
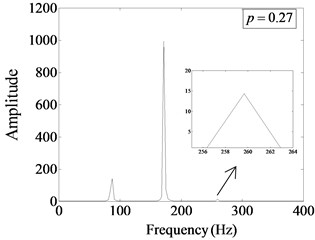
b)
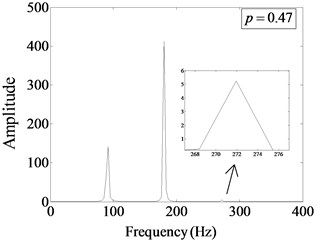
c)
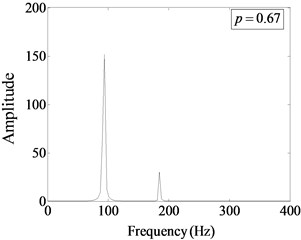
d)
3.3. Damage detection of breathing crack
3.3.1. Distortion value of phase spectrum,
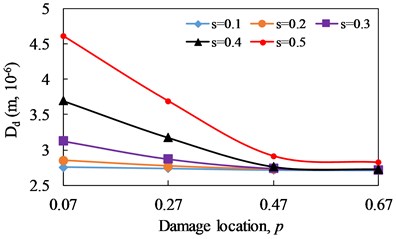
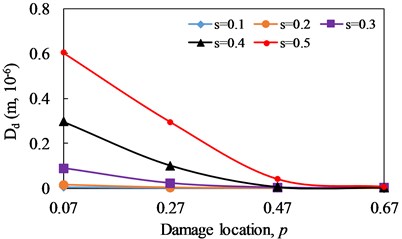
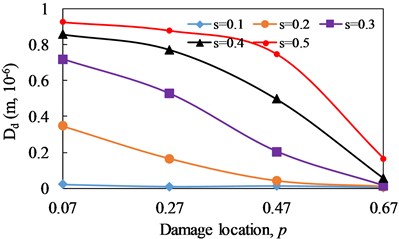
The evolutions of with damage severity and damage location are illustrated in Fig. 16 and 17, respectively. For cantilever beam, when the damage location is fixed, increases obviously with the increase of damage severity. And when the damage severity is fixed, the closer the damage is to the fixed end, the larger the value of is. The value of can reflect the damage severity of cracked beam, and the magnitude of is positively correlated with the damage severity. When the damage severity is taken as variable, the change degree of at is the most obvious and it is the weakest at . when the damage location is taken as a variable, the change degree of at is the most obvious and it is the weakest at . It can be seen that is effective for the identification of non-linear fatigue crack in cantilever beam.
Fig. 16Change curve of distortion value of phase spectrum (Dd) with damage severity
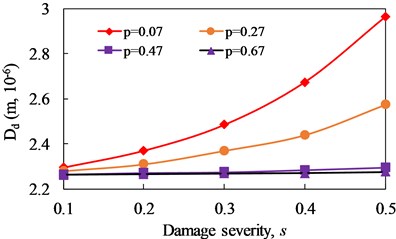
a)1/3
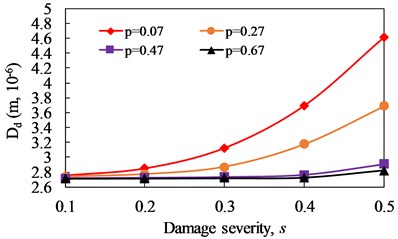
b)1/2
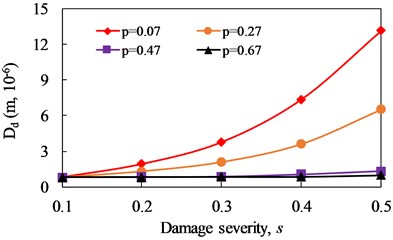
c) 2
Fig. 17Change curve of distortion value of phase spectrum (Dd) with damage location
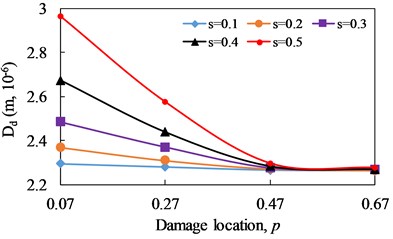
a)1/3
b)1/2
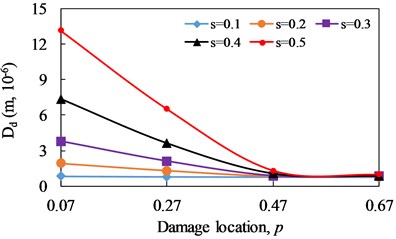
c) 2
3.3.2. Proportion of super/sub-harmonic amplitudes,
The variation curves of the proportion of super/sub-harmonic amplitudes () versus damage severity and damage location are illustrated in Figs. 18 and 19, respectively. As observed from the results, increases with the increase of damage severity when the damage location and excitation frequency are fixed. For the influence of excitation frequency, 1/2 presents more obvious effect on at all damage locations. Moreover, the influence of damage location on decrease with the increase of damage location away from the fixed end. The results reveal that can be used to reflect the damage evolution of fatigue crack in cantilever beam.
3.4. Comparison analysis between contact model and bilinear model
Comparative analysis was conducted for the influence of fatigue crack simulated by contact and bilinear models on and of cracked beam, which are shown in Figs. 20 and 21, respectively. As observed from the results, it is found that the two models keep the same trend under different conditions. At the same damage depth or location, the index values ( and ) of the contact model are higher than those of the bilinear one, which indicates that the contact model with time-varying stiffness can more significantly reflect the nonlinear characteristics of fatigue crack in damage identification of cantilever beam.
Fig. 18Change curve of proportion of super/sub-harmonic amplitudes (hΔ) with damage severity
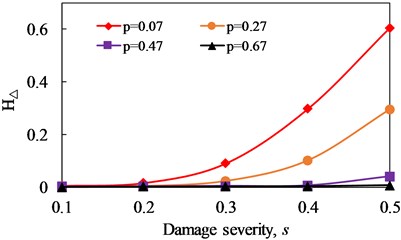
a)1/3
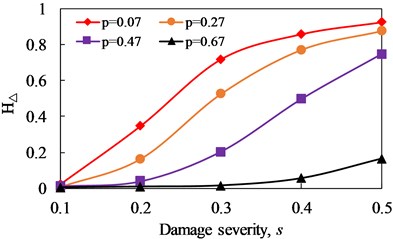
b)1/2
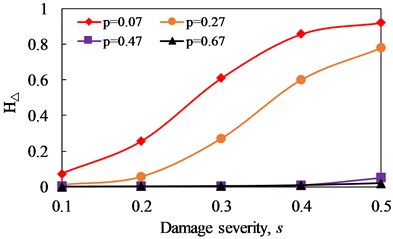
c) 2
Fig. 19Change curve of proportion of super/sub-harmonic amplitudes (hΔ) with damage location
a)1/3
b)1/2
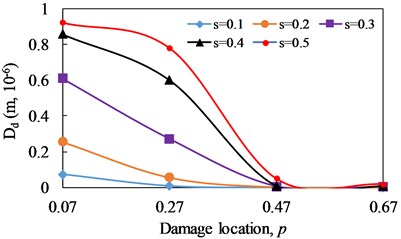
c) 2
Fig. 20Comparison of distortion value of phase spectrum (Dd) between contact and bilinear models
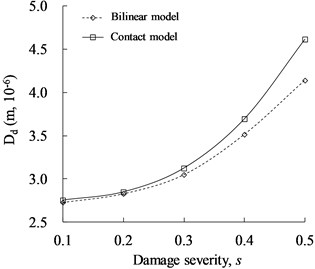
a)
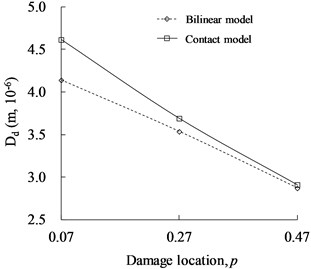
b)
Fig. 21Comparison of proportion of super/sub-harmonic amplitudes (hΔ) between contact and bilinear models
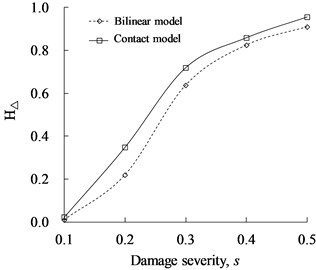
a)
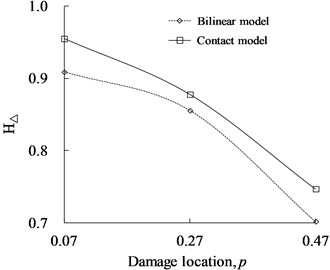
b)
4. Conclusions
In this study, a time-varying stiffness contact model is used to simulate fatigue crack of cantilever beam. The influences of excitation frequency, damage severity and location on harmonic vibration response of structure are analyzed, and the damage identification indexes based on harmonic excitation response is proposed and verified. Moreover, the identification effect of bilinear and contact models is compared and analyzed. Following conclusions can be drawn:
1) An intact cantilever beam model and corresponding damaged one with fatigue crack under different damage conditions are established. By comparing the acceleration time history, phase spectrum and Fourier spectrum obtained by harmonic excitation at different frequencies, it is found that the harmonic vibration response is sensitive and can characterize the occurrence of fatigue damage.
2) The influence of fatigue crack damage on non-linear structural vibration response become intensified as the damage severity and location deterioration. The more the damage severity is, and the closer the damage location is to the fixed end, the more significant the distortion in the acceleration time history, phase spectrum and Fourier spectrum exhibits.
3) Distortion value of phase spectrum () and proportion of super/sub-harmonic amplitudes () can evidently characterize the change of fatigue crack with different damage location and severity. The larger the index value is, the more serious the damage is. They can be used to identify structural fatigue damage.
4) Under the same damage conditions, the bilinear crack model is compared with the contact model. The results show that the contact crack model contains stronger non-linear information, and the change trends of damage indicators are more obvious. The contact model is more suitable for simulating fatigue crack damage.
5) Numerical simulation is performed to verify the effectiveness of contact model in fatigue crack simulation and the sensitivity of proposed damage identification index. In the future, experimental tests will be carried out to validate its feasibility in actual beam structure, and an appropriate damage identification method will be constructed based on the damage identification indexes to realize effective identification of nonlinear fatigue damage.
References
-
M. Abedin and A. B. Mehrabi, “Health monitoring of steel box girder bridges using non-contact sensors,” Structures, Vol. 34, pp. 4012–4024, Dec. 2021, https://doi.org/10.1016/j.istruc.2021.10.021
-
M. Demetgul, K. Yildiz, S. Taskin, I. N. Tansel, and O. Yazicioglu, “Fault diagnosis on material handling system using feature selection and data mining techniques,” Measurement, Vol. 55, pp. 15–24, Sep. 2014, https://doi.org/10.1016/j.measurement.2014.04.037
-
A. J. Hughes, L. A. Bull, P. Gardner, R. J. Barthorpe, N. Dervilis, and K. Worden, “On risk-based active learning for structural health monitoring,” Mechanical Systems and Signal Processing, Vol. 167, p. 108569, Mar. 2022, https://doi.org/10.1016/j.ymssp.2021.108569
-
A. D. Dimarogonas, “Vibration of cracked structures: A state of the art review,” Engineering Fracture Mechanics, Vol. 55, No. 5, pp. 831–857, Nov. 1996, https://doi.org/10.1016/0013-7944(94)00175-8
-
Y. Yao, S.-T. E. Tung, and B. Glisic, “Crack detection and characterization techniques-An overview,” Structural Control and Health Monitoring, Vol. 21, No. 12, pp. 1387–1413, Dec. 2014, https://doi.org/10.1002/stc.1655
-
S. A. Neild, M. S. Williams, and P. D. McFadden, “Nonlinear vibration characteristics of damaged concrete beams,” Journal of Structural Engineering, Vol. 129, No. 2, pp. 260–268, Feb. 2003, https://doi.org/10.1061/(asce)0733-9445(2003)129:2(260)
-
T. G. Chondros, A. D. Dimarogonas, and J. Yao, “Vibration of a beam with a breathing crack,” Journal of Sound and Vibration, Vol. 239, No. 1, pp. 57–67, Jan. 2001, https://doi.org/10.1006/jsvi.2000.3156
-
Y. Ma and G. Chen, “Natural vibration of a beam with a breathing oblique crack,” Shock and Vibration, Vol. 2017, pp. 1–13, 2017, https://doi.org/10.1155/2017/8045347
-
S. Ručevskis, M. Wesolowski, and A. Chate, “Vibration-based damage detection in a beam structure with multiple damage locations,” Aviation, Vol. 13, No. 3, pp. 61–71, Sep. 2009, https://doi.org/10.3846/1648-7788.2009.13.61-71
-
W.-Y. He, S. Zhu, and W.-X. Ren, “Two-phase damage detection of beam structures under moving load using multi-scale wavelet signal processing and wavelet finite element model,” Applied Mathematical Modelling, Vol. 66, pp. 728–744, Feb. 2019, https://doi.org/10.1016/j.apm.2018.10.005
-
H. Cui, X. Xu, W. Peng, Z. Zhou, and M. Hong, “A damage detection method based on strain modes for structures under ambient excitation,” Measurement, Vol. 125, pp. 438–446, Sep. 2018, https://doi.org/10.1016/j.measurement.2018.05.004
-
F. P. Kopsaftopoulos and S. D. Fassois, “A functional model based statistical time series method for vibration based damage detection, localization, and magnitude estimation,” Mechanical Systems and Signal Processing, Vol. 39, No. 1-2, pp. 143–161, Aug. 2013, https://doi.org/10.1016/j.ymssp.2012.08.023
-
M. Cao, Z. Su, L. Cheng, and H. Xu, “A multi-scale pseudo-force model for characterization of damage in beam components with unknown material and structural parameters,” Journal of Sound and Vibration, Vol. 332, No. 21, pp. 5566–5583, Oct. 2013, https://doi.org/10.1016/j.jsv.2013.05.002
-
R. Perera, R. Marin, and A. Ruiz, “Static-dynamic multi-scale structural damage identification in a multi-objective framework,” Journal of Sound and Vibration, Vol. 332, No. 6, pp. 1484–1500, Mar. 2013, https://doi.org/10.1016/j.jsv.2012.10.033
-
A. Mofid Nakhaei, M. Dardel, and M. Hassan Ghasemi, “Modeling and frequency analysis of beam with breathing crack,” Archive of Applied Mechanics, Vol. 88, No. 10, pp. 1743–1758, Oct. 2018, https://doi.org/10.1007/s00419-018-1400-z
-
J. Zeng, H. Ma, W. Zhang, and B. Wen, “Dynamic characteristic analysis of cracked cantilever beams under different crack types,” Engineering Failure Analysis, Vol. 74, pp. 80–94, Apr. 2017, https://doi.org/10.1016/j.engfailanal.2017.01.005
-
A. Benedetti, G. Pignagnoli, and M. Tarozzi, “Damage identification of cracked reinforced concrete beams through frequency shift,” Materials and Structures, Vol. 51, No. 6, Dec. 2018, https://doi.org/10.1617/s11527-018-1275-z
-
J. Prawin, K. Lakshmi, and A. R. M. Rao, “A novel singular spectrum analysis-based baseline-free approach for fatigue-breathing crack identification,” Journal of Intelligent Material Systems and Structures, Vol. 29, No. 10, pp. 2249–2266, Jun. 2018, https://doi.org/10.1177/1045389x18758206
-
S. Smith, G. Wang, and D. Wu, “Bayesian approach to breathing crack detection in beam structures,” Engineering Structures, Vol. 148, pp. 829–838, Oct. 2017, https://doi.org/10.1016/j.engstruct.2017.06.071
-
U. Andreaus, P. Baragatti, P. Casini, and D. Iacoviello, “Experimental damage evaluation of open and fatigue cracks of multi-cracked beams by using wavelet transform of static response via image analysis,” Structural Control and Health Monitoring, Vol. 24, No. 4, p. e1902, Apr. 2017, https://doi.org/10.1002/stc.1902
-
U. Andreaus and P. Baragatti, “Cracked beam identification by numerically analysing the nonlinear behaviour of the harmonically forced response,” Journal of Sound and Vibration, Vol. 330, No. 4, pp. 721–742, Feb. 2011, https://doi.org/10.1016/j.jsv.2010.08.032
-
U. Andreaus, P. Casini, and F. Vestroni, “Non-linear dynamics of a cracked cantilever beam under harmonic excitation,” International Journal of Non-Linear Mechanics, Vol. 42, No. 3, pp. 566–575, Apr. 2007, https://doi.org/10.1016/j.ijnonlinmec.2006.08.007
-
B. Wimarshana, N. Wu, and C. Wu, “Identification of breathing cracks in a beam structure with entropy,” SPIE Smart Structures and Materials + Nondestructive Evaluation and Health Monitoring, Vol. 9804, Apr. 2016, https://doi.org/10.1117/12.2219250
-
M. Y. Zhang, X. Li, W. Z. Qu, and Y. Lu, “Damage detection of fatigue cracks under nonlinear boundary condition using subharmonic resonance,” Ultrasonics, Vol. 77, pp. 152–159, May 2017, https://doi.org/10.1016/j.ultras
-
B. Panigrahi and G. Pohit, “Nonlinear dynamic response of open and breathing cracked functionally graded beam under single and multi-frequency excitation,” Engineering Structures, Vol. 242, p. 112437, Sep. 2021, https://doi.org/10.1016/j.engstruct.2021.112437
-
W. Xu, Z. Su, M. Radzieński, M. Cao, and W. Ostachowicz, “Nonlinear pseudo-force in a breathing crack to generate harmonics,” Journal of Sound and Vibration, Vol. 492, p. 115734, Feb. 2021, https://doi.org/10.1016/j.jsv.2020.115734
-
M. Kharazan, S. Irani, M. A. Noorian, and M. R. Salimi, “Nonlinear vibration analysis of a cantilever beam with multiple breathing edge cracks,” International Journal of Non-Linear Mechanics, Vol. 136, p. 103774, Nov. 2021, https://doi.org/10.1016/j.ijnonlinmec.2021.103774
-
K. Wang, M. Liu, Z. Su, S. Guo, and F. Cui, “Mode-mismatching enhanced disbond detection using material nonlinearity in guided waves at low frequency,” Journal of Sound and Vibration, Vol. 490, p. 115733, Jan. 2021, https://doi.org/10.1016/j.jsv.2020.115733
-
L. Xu et al., “Model-driven fatigue crack characterization and growth prediction: a two-step, 3-D fatigue damage modeling framework for structural health monitoring,” International Journal of Mechanical Sciences, Vol. 195, p. 106226, Apr. 2021, https://doi.org/10.1016/j.ijmecsci.2020.106226
-
L. Xu, Y. Su, K. Wang, X. Yang, S. Yuan, and Z. Su, “An elastodynamic reciprocity theorem-based closed-form solution to second harmonic generation of lamb waves by a fatigue crack: Theory and experimental validation,” Journal of Sound and Vibration, Vol. 509, p. 116226, Sep. 2021, https://doi.org/10.1016/j.jsv.2021.116226
-
S. Basu, A. Thirumalaiselvi, S. Sasmal, and T. Kundu, “Nonlinear ultrasonics-based technique for monitoring damage progression in reinforced concrete structures,” Ultrasonics, Vol. 115, p. 106472, Aug. 2021, https://doi.org/10.1016/j.ultras.2021.106472
Cited by
About this article
The authors express their appreciation for financial support of National Natural Science Foundation of China (grant number 51408258); China Postdoctoral Science Foundation funded project (grant number 2018M642300); Jiangsu Transportation Science Technology Project (grant number 2018Y11), Jiangsu Province Construction System Science and Technology Project (grant number 2021ZD54), and Jiangsu Planned Projects for Postdoctoral Research Funds (grant number 2018K136C).
