The enhancement of fault detection for rolling bearing via optimized VMD and TQWT based sparse code shrinkage

Yuan, Xing; Zhang, Huijie; Liu, Hui

doi:10.21595/jve.2021.22201

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 May 2022

Check for updates

The enhancement of fault detection for rolling bearing via optimized VMD and TQWT based sparse code shrinkage

Xing Yuan¹

Huijie Zhang²

Hui Liu³

^{1, 2, 3}Collaborative Innovation Center of High-End Manufacturing Equipment in Xi’an Jiaotong University, Xi’an, P. R. China

Corresponding Author:

Huijie Zhang

Cite the article Download PDF

Downloads 725

CrossRef Citations 1

Abstract

A typical vibration signal of fault bearing is composed of periodic repetitive transient impulses, multiple vibration disturbance and background noise. Variational mode decomposition (VMD) represents a potential tool for analyzing such signals. However, the reasonable selection of VMD algorithm parameters hinders its application in mechanical signal processing to a certain extent. According to the specific characteristics of rolling bearing fault signal, the composite dimensionless index is constructed as the objective function to ensure the optimal decomposition of VMD. To further enhance the fault characteristics, the tunable Q-factor wavelet transform (TQWT) along with sparse code shrinkage is proposed to denoise the modal components containing periodic impulses, which further highlights the impulses and improves the sparseness of fault signal. Simulation and experimental signal analysis verify the effectiveness and reliability of this method. The results show that the use of optimized VMD and TQWT based sparse code shrinkage dramatically sharpens the impulses from the mixed signal with noise interference and increases the sparseness to a level.

The enhancement of fault detection for rolling bearing via optimized VMD and TQWT based sparse code shrinkage

Highlights

This article investigates novel weak impulse extraction techniques that utilize the optimized VMD and TQWT based sparse code shrinkage to accurately recover the useful transients.
According to the specific characteristics of rolling bearing fault signal, the composite dimensionless index is constructed as the objective function to ensure the optimal decomposition of VMD. These three dimensionless indexes measure the impulse characteristics from different aspects, and can well obtain the optimal mode decomposition of the VMD.
The impulses, which are contained in the optimal component of the optimized VMD, are then enhanced using the TQWT based sparse code shrinkage method, which effectively matches the specific damped oscillation behavior, clarifies the impulses and spares representation fault signal. The reliability and feasibility of the described approach are verified by simulation and test data.

1. Introduction

Rolling bearing is the core of almost every rotating machine. As a common fault source, they have been widely concerned in the field of vibration analysis. Typically, an undamaged bearing generates a steady state vibration, but a fault in any elements of it can change the condition and produce noticeable vibration impulses [1-2]. A successful diagnosis method should be able to isolate the impulse response caused by defects. So far, many different technologies have been proposed to monitor and diagnose rolling bearing fault, such as Wavelet transform (WT) [3-5], Empirical mode decomposition (EMD) [6], Spectral kurtosis (SK) [7-8], Cyclostationary analysis [9-10], Minimum entropy deconvolution (MED) [11], Blind filters [12], etc. Meanwhile, some new systems and fault identification methods for vibration analysis increasingly attract the scholars’ attention [13-18]. Those works also achieved good performances in bearing fault recognition through designing hierarchical architectures and combining various domain representations. However, how to match the local oscillation attenuation characteristics of impulse signal and represent vibration signal sparsely to ensure the accuracy of fault detection is still a challenge in the diagnosis field. There are many reasons for this problem, including the complexity of bearing contact motion, weak dynamic response, aliasing variability, multi-source coupling, mechanical structure filtering and service condition uncertainty. Consequently, we propose a novel hybrid approach of optimized VMD and TQWT based sparse code shrinkage to reduce noise interference, extract impulse feature and enhance signal sparsity.

Unlike EMD, Dragomiretskiy et al. presented a new variational method, which decomposes a signal into a set of band-limited intrinsic mode functions, called variational mode decomposition (VMD) [19]. As soon as VMD is put forward, it has attracted a lot of attention in the field of mechanical fault diagnosis, because of its equivalent filtering characteristics and noise robustness. However, the two key parameters of VMD, i.e., decomposition level and quadratic penalty factor, need to be defined in advance, resulting in suboptimal decomposition performance. Although some researches mainly focus on the adaptive parameters determination, due to the complexity of rolling bearing fault signals, the problem of optimal parameters selection remains to be solved. To make up for the deficiency of single feature in VMD parameters optimization, we try to use multi-parameters fusion method to construct composite feature, so as to obtain the optimal mode decomposition and corresponding component.

In addition to the background noise, the large discrete frequency interference caused by the other mechanical parts often confuses and misleads the detection process. Therefore, it is necessary to further purify the fault signal and realize the sparse representation of weak transient impulse characteristics. The tunable Q-factor wavelet transform (TQWT) proposed by Selesnick is a new over complete wavelet transform, which constructs wavelets in frequency domain, and the optimal matching can be achieved for the characteristic signal components with specific oscillation behavior [20]. Meanwhile, TQWT has the advantage of fast implementation using radix-2 FFTs. Luo and He provided a deep and detailed analysis of TQWT including the filter bank, decomposition level, Q factor and parameter influence [21-22]. Based on TQWT, Selesnick further proposed resonance-based sparse signal decomposition (RSSD) [23], which decomposes the high resonance and low resonance components according to the signal resonance properties. Cai proposed redundant dictionary construction based on TQWT for sparse representation of gearbox vibration signal and studied the sparsity-enhanced signal decomposition method based on signal different morphologies property [24-25]. Zhang and Yu studied the multi-fault diagnosis of gearbox based on RSSD and comb filter [26].

In this article, a new TQWT based sparse code shrinkage method is proposed, which can well match the damped oscillation mode of bearing fault signal and enhance the transient impulse characteristics. For the adaptive parameter selection, the cross-correlation coefficient is employed to optimize the Q factor and decomposition scale to ensure the matching and sparse representation of bearing fault signal. The impulses, which are contained in the optimal component of the optimized VMD, are then enhanced using the TQWT based sparse code shrinkage method, which effectively matches the specific damped oscillation behavior, clarifies the impulses and spares representation fault signal.

This article is organized as follows. Section 2 reviews the basic theory of VMD and introduces the optimized VMD. In Section 3, the implementation of TQWT based sparse code shrinkage is given in detail. In Section 4, we provide simulation experiments to verify the effectiveness of the proposed method. Section 5 presents analysis of actual vibration signal from a bearing with outer and inner race fault, which demonstrates the enhancement of weak impulse signal by using optimized VMD and TQWT based sparse code shrinkage. Finally, some conclusions are drawn in Section 6.

2. Optimized VMD

2.1. Theoretical basis of VMD

As a non-recursive signal decomposition method, VMD has its solid theoretical foundation, which is the generalization of classical Wiener filter in multiple adaptive frequency bands. VMD decomposes the input signal into a series of sub-modes $u_{k}$ with specific sparse characteristics. In frequency domain, the bandwidth of each sub-mode $u_{k}$ is compact near the frequency center, and the bandwidth is estimated by the $L^{2}$ norm of the gradient. The resulting constrained variational problem is the following [19]:

1

\begin{array}{l} \underset{\{u_{k}\}, \{ω_{k}\}}{m i n} \{\sum_{k} {‖\partial_{t} [(δ (t) + \frac{j}{π t}) * u_{k} (t)] e^{- j ω_{k} t}‖}_{2}^{2}\}, \\ s . t . \sum_{k} u_{k} (t) = f, \end{array}

where $\{u_{k}\} = \{u_{1}, u_{2}, \dots u_{k}\}$ and $\{ω_{k}\} = \{ω_{1}, ω_{2}, \dots ω_{k}\}$ are the set of sub-modes and their center frequencies, respectively. Equally, $δ (t)$ is the impulse function and $k$ is the decomposition level.

In VMD algorithm, the quadratic penalty factor $α$ and Lagrange multiplication operator $λ$ are introduced to solve the constrained variational problem. The quadratic penalty factor can ensure the reconstruction accuracy of the signal, and the Lagrange multiplication operator can ensure the accurate execution of the constraints. The enhanced Lagrangian operator $L$ can be described as [19]:

2

L (\{u_{k}\}, \{ω_{k}\}, λ) : = α \sum_{k} {‖\partial_{t} [(δ (t) + \frac{j}{π t}) * u_{k} (t)] e^{- j ω_{k} t}‖}_{2}^{2}

+ {‖f (t) - \sum_{k} u_{k} (t)‖}_{2}^{2} + ⟨λ (t), f (t) - \sum_{k} u_{k} (t)⟩ .

The original minimization problem Eq. (1) is transformed into problem Eq. (2), which is solved by alternate direction method of multipliers (ADMM). Firstly, the number of decomposition modes is determined, and the sub-modes ${\hat{u}}_{k}^{1}$ , the corresponding center frequency $ω_{k}^{1}$ and Lagrange operator $λ^{1}$ are initialized. Then, the sub-mode ${\hat{u}}_{k}$ and the center frequency $ω_{k}$ are updated by Eq. (3) and Eq. (4), respectively:

3

{\hat{u}}_{k}^{n + 1} (ω) \leftarrow \frac{\hat{f} (ω) - \sum_{i < k} {\hat{u}}_{i}^{n + 1} (ω) - \sum_{i > k} {\hat{u}}_{i}^{n} (ω) + {\hat{λ}}^{n} (ω) / 2}{1 + 2 α {(ω - ω_{k}^{n})}^{2}},

4

ω_{k}^{n + 1} \leftarrow \frac{\int_{0}^{\infty} ω {|{\hat{u}}_{k}^{n + 1} (ω)|}^{2} d ω}{\int_{0}^{\infty} {|{\hat{u}}_{k}^{n + 1} (ω)|}^{2} d ω} .

The Lagrange operator is updated by Eq. (5):

5

{\hat{λ}}^{n + 1} (ω) \leftarrow {\hat{λ}}^{n} (ω) + τ (\hat{f} (ω) - \sum_{k} {\hat{u}}_{k}^{n + 1} (ω)),

where $τ$ denotes the tolerance parameter of noise.

While the following convergence condition is satisfied, the iteration is terminated:

6

\sum_{k} \frac{{‖{\hat{u}}_{k}^{n + 1} - {\hat{u}}_{k}^{n}‖}_{2}^{2}}{{‖{\hat{u}}_{k}^{n}‖}_{2}^{2}} < ε,

where $ε$ is the convergence error. The noise tolerance $τ$ and convergence error $ε$ have little influence on the decomposition result, so the default values are usually used.

2.2. Parameter optimization method

As a parametric signal decomposition method, VMD involves two key parameters, which have a crucial impact on the decomposition results. A key parameter is the decomposition level $k$ . If decomposition level is too large or too small, it is not conducive to the signal decomposition, thus affecting the recognition accuracy of information features. Another key parameter is penalty factor $α$ . The penalty factor determines the bandwidth of each mode component. To obtain the impulse characteristics of bearing fault as much as possible, we synthesize multiple dimensionless indexes to form a composite characteristic index, so as to optimize and screen two key parameters. In other words, the largest average composite index of mode components corresponds to two key parameters of optimization. Three dimensionless indexes are selected, which are kurtosis $K$ , peak factor $P$ and margin factor $M$ . These three dimensionless indexes measure the impulse characteristics from different aspects, and can well obtain the optimal mode decomposition of the VMD. To maintain the balance between indicators and increase the comparability, we use the relative ratio to construct the composite index $C$ :

7

C = {(\frac{K_{u}}{K})}^{1 / 2} + {(\frac{P_{u}}{P})}^{1 / 2} + {(\frac{M_{u}}{M})}^{1 / 2},

where $K_{u}$ , $P_{u}$ and $M_{u}$ are the corresponding indexes of VMD decomposition components, and $K$ , $P$ and $M$ are the corresponding indexes of original signal respectively.

After the optimization parameters are determined, the sensitive component of VMD is then judged according to the kurtosis maximization criterion. It is easy to see that the extracted sensitive component contains more bearing fault information, which is conducive to the subsequent impulse feature enhancement.

3. TQWT and sparse code shrinkage algorithm

3.1. Tunable Q-factor wavelet transform

According to the above analysis, the optimized VMD can adaptively extract the mode components with more impulse information, but the extracted impulse will still contain a lot of noise interference. It is well known that impulse signal has non-Gaussian statistical characteristics, while noise in vibration signal is generally considered as Gaussian distribution. Therefore, a new TQWT based sparse code shrinkage algorithm is proposed for sparse representation of the mode component to further highlight the periodic impulses.

The difference between TQWT and dyadic wavelet transform is that TQWT realizes $Q$ -factor adjustment and redundant operation by iterating filter banks through low pass scale factor $α$ and high pass scale factor $β$ , shown in Fig. 1. This design concept can not only extract the oscillation mode, but also obtain the detailed characteristics, which is very suitable for matching the attenuation oscillation mode of rolling bearing fault signal.

Fig. 1Analysis and synthesis filter bank for the tunable-Q wavelet transform

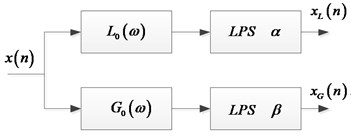
a) Analysis filter bank

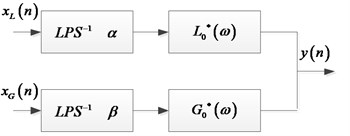
b) Synthesis filter bank

TQWT directly designates quality factor $Q$ and redundancy factor $r$ to design wavelet, which further increases the flexibility of quality factor selection and makes wavelet acquisition more convenient. After $Q$ and $r$ are selected, $α$ and $β$ can be obtained by [20]:

8

β = \frac{2}{1 + Q}, α = 1 - \frac{β}{r} .

The expressions of low pass filter and high pass filter are as follows:

9

\{\begin{array}{l} L_{0} (ω) = 1, |ω| \leq (1 - β) π, \\ L_{0} (ω) = θ (\frac{ω + (β - 1) π}{α + β - 1}), (1 - β) π < |ω| < α π, \\ L_{0} (ω) = 0, α π \leq |ω| \leq π, \end{array}

10

\{\begin{array}{l} G_{0} (ω) = 0, |ω| \leq (1 - β) π, \\ G_{0} (ω) = θ (\frac{α π - ω}{α + β - 1}), (1 - β) π < |ω| < α π, \\ G_{0} (ω) = 1, α π \leq |ω| \leq π, \end{array}

where $θ (ω) = 0.5 (1 + c o s ω) \sqrt{2 - c o s ω}$ , $|ω| \leq π$ .

Furthermore, the decomposition level $J$ is limited by the length of the signal $N$ . Their relation can be expressed as:

11

J \leq \frac{l o g (\frac{β N}{8})}{l o g (\frac{1}{α})} .

When $0 < α \leq 1$ , the input signal is set as $X (ω)$ , and the low-scale filtering characteristic of the corresponding output signal $Y (ω)$ is expressed as follows:

12

Y (ω) = X (α ω), |ω| \leq π .

If $α \geq 1$ :

13

Y (ω) = \{\begin{array}{l} X (α ω), |ω| \leq π / α, \\ 0, π / α < |ω| \leq π . \end{array}

For the high scale, when $0 < β \leq 1$ , the filtering characteristic is given by:

14

Y (ω) = \{\begin{array}{l} X (β ω + (1 - β) π), 0 < ω < π, \\ X (β ω - (1 - β) π), - π < ω < 0 . \end{array}

If $β \geq 1$ :

15

Y (ω) = \{\begin{array}{l} \begin{array}{l} X (β ω + (1 - β) π), (1 - 1 / β) π < ω < π, \\ X (β ω - (1 - β) π), - π < ω < - (1 - 1 / β) π, \end{array} \\ 0, |ω| < (1 - 1 / β) π . \end{array}

According to the frequency domain characteristics of high-low-pass filter and its subsequent high-low-pass scale transformation, combining with the iterative operation of the basic filter banks under the multi-scale decomposition, the equivalent frequency response function for the $j$ th stage is given by [20]:

16

L_{j} (ω) = \{\begin{array}{l} \prod_{m = 0}^{j - 1} L_{0} (\frac{ω}{α^{m}}), |ω| \leq α^{j} π, \\ 0, α^{j} π < |ω| < π, \end{array}

17

G_{j} (ω) = \{\begin{array}{l} G_{0} (\frac{ω}{α^{j - 1}}) \prod_{m = 0}^{j - 2} L_{0} (\frac{ω}{α^{m}}), (1 - β) α^{j - 1} π < |ω| \leq α^{j - 1} π, \\ 0, |ω| \leq π . \end{array}

3.2. Sparse code shrinkage

The SCS algorithm [27] proposed by Hyvarinen uses the statistical characteristics of non-Gaussian components to get the threshold shrinkage function, and denoises the measured signal by removing the noise with the same or similar frequency as the target signal. The sparse representation of bearing vibration signal can be realized by SCS algorithm, because the fault-generated impulse is strongly non-Gaussian in statistical characteristic. Actually, the local damage vibration signal of rolling bearing is characterized by Non-Gaussian property, repetitive transient impulse waveform and typical sparseness.

Assume $x_{f}$ is the original fault signal and $v$ is Gaussian noise of zero mean and variance $σ^{2}$ , then the observed signal $x$ is given by:

18

x = x_{f} + v .

To represent a sparse distribution, Hyvarinen proposes the following probability density function of a sparse signal [27]:

19

p (x_{f}) = \frac{1}{2 d} \frac{(α + 2) {[α (α + 1) / 2]}^{(α / 2 + 1)}}{{[\sqrt{α (α + 1) / 2} + |x_{f} / d|]}^{(α + 3)}},

where $d$ is the standard deviation of fault impulse signal $x_{f}$ and $α$ is a parameter controlling the sparseness of the probability density function. In this article, we set $α$ = 0.1 to adapt bearing fault feature extraction [5].

For the sparse signal with this distribution, the following thresholding rule can be obtained according to the maximum likelihood principle [27]:

20

{\tilde{x}}_{f} = s i g n (x) m a x (0, \frac{|x| - a d}{2} + \frac{1}{2} \sqrt{{(|x| + a d)}^{2} - 4 σ^{2} (α + 3)}),

where $a = \sqrt{α (α + 1) / 2}$ , $σ$ is the standard deviation of the noise, and $x_{f}$ is set to zero in the case that the square root in above equation is imaginary. The SCS algorithm is used as TQWT threshold and the noise standard deviation is estimated for each scale [28-29]:

21

σ = m a d / 0.6745,

where $m a d$ denotes the median absolute deviation of wavelet coefficients.

Assume $x$ is zero mean, for $x$ and $v$ are uncorrelated, the standard deviation $d$ of $x_{f}$ can be estimated by [28-29]:

22

d = \sqrt{σ_{x}^{2} - σ^{2}} .

It is worth noting that the standard deviation $d$ needs to be calculated separately on each wavelet scale.

3.3. Adaptive sparse representation

As a new explicit wavelet construction theory in frequency domain, TQWT has the advantages of matching specific oscillation behavior of signal components and fast implementation by FFT algorithm. SCS is a useful tool for signal sparse representation. Naturally, the TQWT along with SCS can efficiently implement multi-scale sparse decomposition of dynamic signals.

For TQWT, as mentioned before, three parameters need to be determined: the $Q$ -factor, the decomposition level $J$ and redundancy $r$ . The specified value of the redundancy must satisfy that $r > 1$ . In this work, the redundancy $r$ is set to 3 by considering the translation invariance and complex calculations. The decomposition level $J$ only affects the frequency domain decomposition performance in low frequency region. Too many decomposition levels will lead to high computational cost, and may lead to excessive decomposition or redundant decomposition of fault characteristic frequency band information. The selection of $J$ should meet the requirements of Eq. (11). $Q$ is an important parameter, which directly affects the extent of wavelet sustained oscillation. We know that the bearing fault signal has local attenuation oscillation behavior. Therefore, the selection of $Q$ has an important influence on matching the bearing fault signal.

The signal processed by TQWT based sparse code shrink has obvious sparsity, and the periodic impulse characteristics are significantly enhanced. Since cross-correlation coefficient directly reflects the similarity of two signals, it is utilized to adaptively determine $Q$ and $J$ . Cross-correlation coefficient $C$ is formulated as:

23

C = \frac{\sum_{n = 0}^{N} (u (n) - \bar{u}) (x (n) - \bar{x})}{{[\sum_{n = 0}^{N} {(u (n) - \bar{u})}^{2} {(x (n) - \bar{x})}^{2}]}^{1 / 2}},

where $x (n)$ is the TQWT reconstruction signal in optimization process, and $u (n)$ is the sensitive component of optimized VMD.

The higher the degree of similarity and matching between the two signals is, the greater the $C$ value is. In general, $C$ can not only ensure that the detected impulses are not lost, but also ensure that the local attenuation oscillation waveform matches well. Therefore, the maximized $C$ is selected as the optimization objective, and the defect occurrence can be effectively judged through the analysis of the time domain waveform and envelope spectrum under these parameters.

4. Simulation experiment

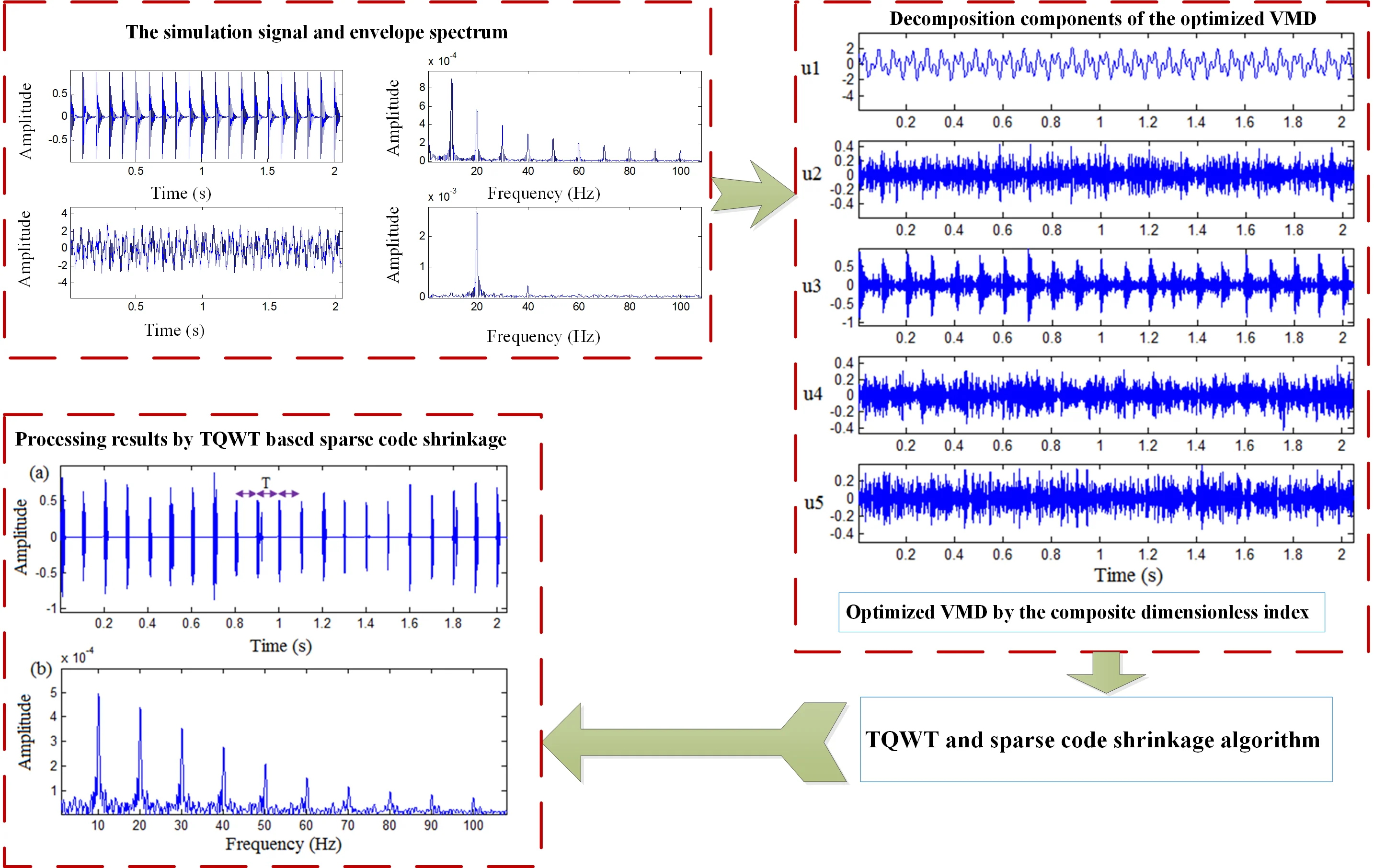
The schematic diagram of the optimized VMD and TQWT based sparse code shrinkage method is shown in Fig. 2. In this section, a signal is used to simulate the fault signal generated by bearing local damage fault to analyze the performance of the proposed method. The mixed signal $x (t)$ consists of three parts: periodic impulse signal $H (t)$ , periodic interference component $s (t)$ and white noise $n (t)$ . The simulated signal is described below:

24

\begin{array}{l} x (t) = H (t) + s (t) + n (t), \\ H (t) = \sum_{k} A_{k} h (t - 1 / f - λ_{i}), \\ h (t) = e^{- 40 t} s i n (2 π 500 t), \\ s (t) = s i n (2 π 15 t) + s i n (2 π 30 t), \\ n (t) = r a n d (n), \end{array}

where $f$ = 10 Hz is impulse interval frequency. $A_{k}$ and $λ_{i}$ respectively represent the amplitude and phase of the impulse signal, and the sampling frequency is set to 2000 Hz.

The time waveform and envelope spectrum of the simulated signal are shown in Fig. 3. Obviously, the impulse components are submerged in strong noise, and it is difficult to find the conspicuous features relevant to periodic impulses. The envelope spectrum is also covered by noise, and most of the spectrum lines are very weak except the 20 Hz spectrum line. Fig. 4 shows the decomposition results of optimized VMD ( $k$ = 5 and $α$ = 500), and $U_{3}$ is automatically selected as the sensitive component according to the kurtosis criterion. As observed in Fig. 5, the periodic transients are clearly revealed by using TQWT ( $Q$ = 1.5 and $J$ = 6) based sparse code shrinkage method. The periodic impulses are very obvious, and the impulse period $T$ can be easily identified by the waveform. Meanwhile, the proposed method achieves better performance in envelope spectrum. It can be seen that the comprehensive use of optimized VMD and TQWT based sparse code shrinkage has good reliability and feasibility in sparse enhancement and weak impulse feature extraction.

Fig. 2Flow chart of the proposed method

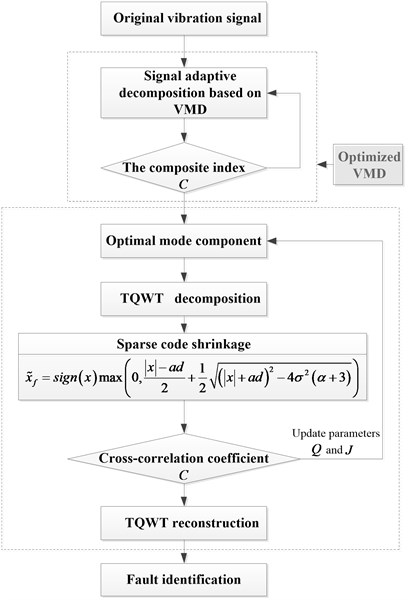
Fig. 3The simulation signal and envelope spectrum: a) periodic impulse signal; b) envelope spectrum of periodic impulse signal; c) mixed signal; d) envelope spectrum of mixed signal

The simulation signal and envelope spectrum: a) periodic impulse signal; b) envelope spectrum of periodic impulse signal; c) mixed signal; d) envelope spectrum of mixed signal

Fig. 4Decomposition components of the optimized VMD

Fig. 5Processing results by TQWT based sparse code shrinkage: a) time domain waveform, b) envelope spectrum

5. Experimental verification and comparative studies

5.1. Experimental verification

The test rig (ABLT-1A) is shown in Fig. 6. ABLT-1A can test four bearings at a time. Four bearings are installed on one shaft. The four test bearings are type 6309. The rotation speed is kept constant at 3000 r/min. The vibration signal is measured by the probe sensor directly contacting the bearing outer race, and the sampling frequency is 48K. The structural parameters of 6309 are as follows: pitch diameter – 72.5 mm, ball diameter – 17.462 mm, ball number – 8. Thus, the fault frequencies of outer race and inner race are $f_{o} =$ 151.829 Hz and $f_{i} =$ 248.171 Hz, respectively.

Due to the large noise in test process, the vibration signals are disordered, and the impulse characteristic signals are almost completely submerged, so the useful fault information cannot be obtained. The proposed optimized VMD ( $k$ = 3 and $α$ = 200) approach is applied to decompose outer race fault signal from the noisy observation, as shown in Fig. 7. According to kurtosis criterion, $U_{2}$ is automatically identified as sensitive component.

Fig. 6ABLT-1A test rig

Fig. 7Outer race fault signal and decomposition components of the optimized VMD

Fig. 8Processing results by TQWT based sparse code shrinkage: a) time domain waveform, b) envelope spectrum, c) envelope spectrum of original signal

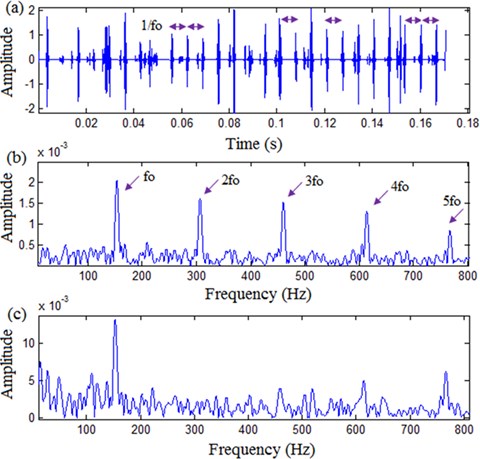
Furthermore, the processing results by using TQWT ( $Q$ = 1.8 and $J$ = 9) based sparse code shrinkage is illustrated in Fig. 8(a) and (b). It can be observed that the useful fault features of outer race can be detected clearly. As expected, the repeated impulse period 1/ $f o$ are clearly revealed and the fault frequency $f_{o}$ and its harmonic components 2 $f_{o}$ , 3 $f_{o}$ , 4 $f_{o}$ , 5 $f_{o}$ are also clearly displayed in envelope spectrum. Although the envelope spectrum of original signal shows significant magnitude at fault frequency $f_{o}$ , many harmonic components are lost, which is disadvantageous to fault identification, as displayed in Fig. 8(c).

Fig. 9Inner race fault signal and decomposition components of the optimized VMD

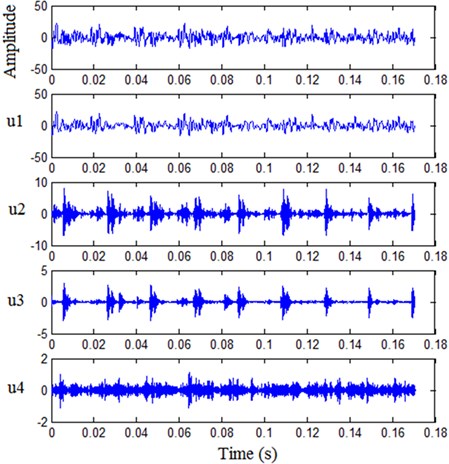
Fig. 10Processing results by TQWT based sparse code shrinkage: a) time domain waveform, b) envelope spectrum, c) envelope spectrum of original signal

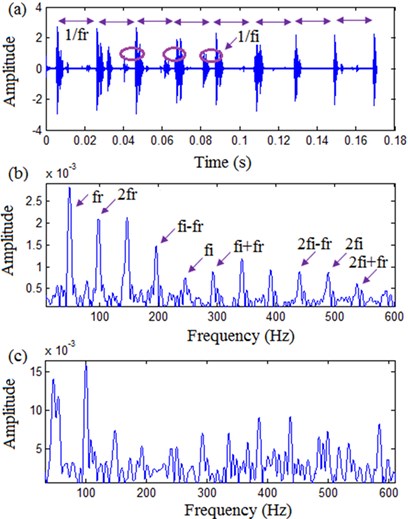
The proposed approach is adopted to analyze inner race fault signal. Inner race fault signal and decomposition components of the optimized VMD ( $k$ = 4 and $α$ = 200) are illustrated in Fig. 9. Similarly, U3 is automatically identified as sensitive component. The processing results by TQWT ( $Q$ = 2.6 and $J$ = 6) based sparse code shrinkage are displayed in Fig. 10. It can be seen that the result is sparse and has periodic structure. It should be noted that when there is a fault on the inner race surface, the fault frequency $f_{i}$ will be modulated by the rotating frequency $f_{r}$ because the damage area is rotating with the rotating shaft. This phenomenon is well reflected in Fig. 10(a) and 10(b), which may improve the accuracy of decisions in fault detection. Nevertheless, it is not easy to get useful fault information through envelope spectrum directly as shown in Fig. 10(c).

From the above experimental signal analysis results, it can be seen that the proposed approach is an effective tool for sparse enhancement and weak impulse extraction.

5.2. Comparative studies

As one of the powerful tools for detecting cyclostationarity signals, spectral correlation can effectively identify the periodic impulses caused by local damage of rolling bearings [7-9]. Fig. 11 illustrates the processing results of the spectral correlation. Although the fault frequency of outer race can be identified in the enhanced envelope spectrum, the effect is far from satisfactory because the harmonic components of fault frequency are not well reflected. In fact, due to the influence of the noisy working environment, the vibration transmission path and the variation of workload, the periodic impulses in vibration signals are overwhelmed by heavy background noise, which makes it difficult to effectively extract the impulse features.

Fig. 11Processing results of vibration signal by Fast-SC

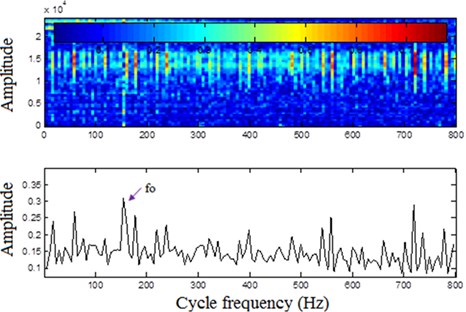
Fig. 12Processing results of vibration signal by MED

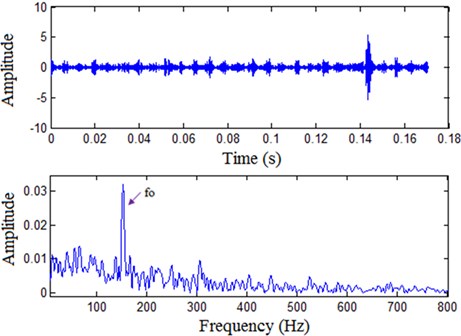
In addition, the MED method [11] is also used to process the vibration signal, and the processing results obtained are shown in Fig. 12. Although there is a rich literature by using the MED, its use is still limited for machine condition monitoring and fault diagnosis because the MED is prone to detect dominant impulses, which are usually unrelated with the information of interest. It can be observed that Fig. 12 can only clearly display the fault frequency of outer race; and it is difficult to distinguish the harmonic components of fault frequency from background noise similar to spectral correlation.

Through the above comparative analysis, it is found that compared with the spectral correlation and MED, the presented method can increase the accuracy of periodic impulse features extraction and is beneficial to the fault diagnosis of rolling bearing.

6. Conclusions

Periodic impulse often carries important information about the running state of rolling bearings. This article investigates novel weak impulse extraction techniques that utilize the optimized VMD and TQWT based sparse code shrinkage to accurately recover the useful transients. A composite dimensionless index suitable for revealing impulse signal is constructed to guide the adaptive decomposition of VMD. Then, the sensitive component is selected according to the kurtosis criterion. Further, the proposed approach exploits sparse code shrinkage in the tunable Q-factor wavelet domain. In general, the proposed approach can preserve the oscillatory behavior of useful transients while still promote the periodic impulse sparsity.

The reliability and feasibility of the described approach are verified by simulation and test data. The results demonstrate that the described approach can extract weak impulse and sparsely represent rolling bearing fault features.

References

R. B. Randall and J. Antoni, “Rolling element bearing diagnostics-A tutorial,” Mechanical Systems and Signal Processing, Vol. 25, No. 2, pp. 485–520, Feb. 2011, https://doi.org/10.1016/j.ymssp.2010.07.017

Publisher
H. Cao, L. Niu, S. Xi, and X. Chen, “Mechanical model development of rolling bearing-rotor systems: A review,” Mechanical Systems and Signal Processing, Vol. 102, pp. 37–58, Mar. 2018, https://doi.org/10.1016/j.ymssp.2017.09.023

Publisher
R. Yan, R. X. Gao, and X. Chen, “Wavelets for fault diagnosis of rotary machines: A review with applications,” Signal Processing, Vol. 96, pp. 1–15, Mar. 2014, https://doi.org/10.1016/j.sigpro.2013.04.015

Publisher
J. Lin and L. Qu, “Feature extraction based on Morlet wavelet and its application for mechanical fault diagnosis,” Journal of Sound and Vibration, Vol. 234, No. 1, pp. 135–148, Jun. 2000, https://doi.org/10.1006/jsvi.2000.2864

Publisher
J. Lin, M. J. Zuo, and K. R. Fyfe, “Mechanical fault detection based on the wavelet de-noising technique,” Journal of Vibration and Acoustics, Vol. 126, No. 1, pp. 9–16, Jan. 2004, https://doi.org/10.1115/1.1596552

Publisher
J. Zheng, J. Cheng, and Y. Yang, “Generalized empirical mode decomposition and its applications to rolling element bearing fault diagnosis,” Mechanical Systems and Signal Processing, Vol. 40, No. 1, pp. 136–153, Oct. 2013, https://doi.org/10.1016/j.ymssp.2013.04.005

Publisher
J. Antoni, “The spectral kurtosis: a useful tool for characterising non-stationary signals,” Mechanical Systems and Signal Processing, Vol. 20, No. 2, pp. 282–307, Feb. 2006, https://doi.org/10.1016/j.ymssp.2004.09.001

Publisher
J. Antoni and R. B. Randall, “The spectral kurtosis: application to the vibratory surveillance and diagnostics of rotating machines,” Mechanical Systems and Signal Processing, Vol. 20, No. 2, pp. 308–331, Feb. 2006, https://doi.org/10.1016/j.ymssp.2004.09.002

Publisher
J. Antoni, F. Bonnardot, A. Raad, and M. El Badaoui, “Cyclostationary modelling of rotating machine vibration signals,” Mechanical Systems and Signal Processing, Vol. 18, No. 6, pp. 1285–1314, Nov. 2004, https://doi.org/10.1016/s0888-3270(03)00088-8

Publisher
I. Antoniadis and G. Glossiotis, “Cyclostationary analysis of rolling-element bearing vibration signals,” Journal of Sound and Vibration, Vol. 248, No. 5, pp. 829–845, Dec. 2001, https://doi.org/10.1006/jsvi.2001.3815

Publisher
N. Sawalhi, R. B. Randall, and H. Endo, “The enhancement of fault detection and diagnosis in rolling element bearings using minimum entropy deconvolution combined with spectral kurtosis,” Mechanical Systems and Signal Processing, Vol. 21, No. 6, pp. 2616–2633, Aug. 2007, https://doi.org/10.1016/j.ymssp.2006.12.002

Publisher
C. Peeters, J. Antoni, and J. Helsen, “Blind filters based on envelope spectrum sparsity indicators for bearing and gear vibration-based condition monitoring,” Mechanical Systems and Signal Processing, Vol. 138, p. 106556, Apr. 2020, https://doi.org/10.1016/j.ymssp.2019.106556

Publisher
D. Kolar, D. Lisjak, M. Pająk, and M. Gudlin, “Intelligent fault diagnosis of rotary machinery by convolutional neural network with automatic hyper-parameters tuning using Bayesian optimization,” Sensors, Vol. 21, No. 7, p. 2411, Mar. 2021, https://doi.org/10.3390/s21072411

Publisher
M. Pająk, Muślewski, B. Landowski, and A. Grządziela, “Fuzzy identification of the reliability state of the mine detecting ship propulsion system,” Polish Maritime Research, Vol. 26, No. 1, pp. 55–64, Mar. 2019, https://doi.org/10.2478/pomr-2019-0007

Publisher
D. Kolar, D. Lisjak, M. Pająk, and D. Pavković, “Fault diagnosis of rotary machines using deep convolutional neural network with wide three axis vibration signal input,” Sensors, Vol. 20, No. 14, p. 4017, Jul. 2020, https://doi.org/10.3390/s20144017

Publisher
G. Tang, Q. Yang, H.-Q. Wang, G.-G. Luo, and J.-W. Ma, “Sparse classification of rotating machinery faults based on compressive sensing strategy,” Mechatronics, Vol. 31, pp. 60–67, Oct. 2015, https://doi.org/10.1016/j.mechatronics.2015.04.006

Publisher
Z. Qi, Y. Tian, and Y. Shi, “Robust twin support vector machine for pattern classification,” Pattern Recognition, Vol. 46, No. 1, pp. 305–316, Jan. 2013, https://doi.org/10.1016/j.patcog.2012.06.019

Publisher
K. Yu, T. R. Lin, H. Ma, X. Li, and X. Li, “A multi-stage semi-supervised learning approach for intelligent fault diagnosis of rolling bearing using data augmentation and metric learning,” Mechanical Systems and Signal Processing, Vol. 146, p. 107043, Jan. 2021, https://doi.org/10.1016/j.ymssp.2020.107043

Publisher
K. Dragomiretskiy and D. Zosso, “Variational mode decomposition,” IEEE Transactions on Signal Processing, Vol. 62, No. 3, pp. 531–544, Feb. 2014, https://doi.org/10.1109/tsp.2013.2288675

Publisher
I. W. Selesnick, “Wavelet transform with tunable Q-factor,” IEEE Transactions on Signal Processing, Vol. 59, No. 8, pp. 3560–3575, Aug. 2011, https://doi.org/10.1109/tsp.2011.2143711

Publisher
J. Luo, D. Yu, and M. Liang, “A kurtosis-guided adaptive demodulation technique for bearing fault detection based on tunable-Q wavelet transform,” Measurement Science and Technology, Vol. 24, No. 5, p. 055009, May 2013, https://doi.org/10.1088/0957-0233/24/5/055009

Publisher
He W. P. et al., “Tunable Q-factor wavelet transform denoising with neighboring coefficients and its application to rotating machinery fault diagnosis,” Science China Technological Sciences, Vol. 56, No. 8, pp. 1956–1965, 2013.

Publisher
I. W. Selesnick, “Resonance-based signal decomposition: A new sparsity-enabled signal analysis method,” Signal Processing, Vol. 91, No. 12, pp. 2793–2809, Dec. 2011, https://doi.org/10.1016/j.sigpro.2010.10.018

Publisher
G. Cai, X. Chen, and Z. He, “Sparsity-enabled signal decomposition using tunable Q-factor wavelet transform for fault feature extraction of gearbox,” Mechanical Systems and Signal Processing, Vol. 41, No. 1-2, pp. 34–53, Dec. 2013, https://doi.org/10.1016/j.ymssp.2013.06.035

Publisher
G. Cai, I. W. Selesnick, S. Wang, W. Dai, and Z. Zhu, “Sparsity-enhanced signal decomposition via generalized minimax-concave penalty for gearbox fault diagnosis,” Journal of Sound and Vibration, Vol. 432, pp. 213–234, Oct. 2018, https://doi.org/10.1016/j.jsv.2018.06.037

Publisher
D. Zhang and D. Yu, “Multi-fault diagnosis of gearbox based on resonance-based signal sparse decomposition and comb filter,” Measurement, Vol. 103, pp. 361–369, Jun. 2017, https://doi.org/10.1016/j.measurement.2017.03.006

Publisher
A. Hyvärinen, “Sparse code shrinkage: denoising of nongaussian data by maximum likelihood estimation,” Neural Computation, Vol. 11, No. 7, pp. 1739–1768, Oct. 1999, https://doi.org/10.1162/089976699300016214

Publisher
D. L. Donoho, “De-noising by soft-thresholding,” IEEE Transactions on Information Theory, Vol. 41, No. 3, pp. 613–627, May 1995, https://doi.org/10.1109/18.382009

Publisher
D. L. Donoho and I. M. Johnstone, “Ideal spatial adaptation by wavelet shrinkage,” Biometrika, Vol. 81, No. 3, pp. 425–455, Sep. 1994, https://doi.org/10.2307/2337118

Publisher

Cited by

Proceedings of International Conference on Artificial Intelligence and Communication Technologies (ICAICT 2023)

Xiao-Rong You

(2024)

About this article

Received

03 September 2021

Accepted

27 December 2021

Published

15 May 2022

SUBJECTS

Fault diagnosis based on vibration signal analysis

DOI

https://doi.org/10.21595/jve.2021.22201

Keywords

rolling bearing

fault diagnosis

optimized variational mode decomposition

tunable Q-factor wavelet transform

sparse code shrinkage

Acknowledgements

This work was financially supported by the Key-Area Research and Development Program of Guangdong Province (Grant No. 2020B090927002) and the project of National Natural Science Funds of Shaanxi Province (Grant No. 2021JM-017) and the National Natural Science Foundation of China (Grant No. 51975462).

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2024 01 21

Rolling bearing fault diagnosis based on variational mode decomposition and weighted multidimensional feature entropy fusion

Na Lei, Feihu Huang, Chunhui Li

Research article

2023 08 01

Motor rolling bearing fault diagnosis based on MVMD energy entropy and GWO-SVM

Jian Tang, Qiaoni Zhao

Research article

2023 08 01

Rolling bearing fault diagnosis method based on ELMD hybrid feature extraction and wavelet neural network

Hengxin Yue, Xihui Chen, Xinhui Shi, Wei Lou

Research article

2022 11 30

Rolling bearing weak fault diagnosis utilizing successive variational mode decomposition with sparsity index reconstructing strategy

Lijie Jiang, Hongchao Wang, Wenliao Du

X. Yuan, H. Zhang, and H. Liu, “The enhancement of fault detection for rolling bearing via optimized VMD and TQWT based sparse code shrinkage,” Journal of Vibroengineering, Vol. 24, No. 3, pp. 453–467, May 2022, https://doi.org/10.21595/jve.2021.22201

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2021.22201
UR  - https://doi.org/10.21595/jve.2021.22201
TI  - The enhancement of fault detection for rolling bearing via optimized VMD and TQWT based sparse code shrinkage
T2  - Journal of Vibroengineering
AU  - Yuan, Xing
AU  - Zhang, Huijie
AU  - Liu, Hui
PY  - 2022
DA  - 2022/01/30
PB  - JVE International Ltd.
SP  - 453-467
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Yuan_2022,
	doi = {10.21595/jve.2021.22201},
	url = {https://doi.org/10.21595/jve.2021.22201},
	year = 2022,
	month = {jan},
	publisher = {{JVE} International Ltd.},
	pages = {453--467},
	author = {Xing Yuan and Huijie Zhang and Hui Liu},
	title = {The enhancement of fault detection for rolling bearing via optimized {VMD} and {TQWT} based sparse code shrinkage},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]X. Yuan, H. Zhang, and H. Liu, “The enhancement of fault detection for rolling bearing via optimized VMD and TQWT based sparse code shrinkage,” Journal of Vibroengineering, pp. 453–467, Jan. 2022, doi: 10.21595/jve.2021.22201.

Copy IEEE

Copied to clipboard!

Yuan, Xing, Huijie Zhang, and Hui Liu. “The Enhancement of Fault Detection for Rolling Bearing via Optimized VMD and TQWT Based Sparse Code Shrinkage.” Journal of Vibroengineering, January 30, 2022, 453–67. https://doi.org/10.21595/jve.2021.22201.

Copy Chicago

Copied to clipboard!

The enhancement of fault detection for rolling bearing via optimized VMD and TQWT based sparse code shrinkage

Abstract

Highlights

1. Introduction

2. Optimized VMD

2.1. Theoretical basis of VMD

2.2. Parameter optimization method

3. TQWT and sparse code shrinkage algorithm

3.1. Tunable Q-factor wavelet transform

3.2. Sparse code shrinkage

3.3. Adaptive sparse representation

4. Simulation experiment

5. Experimental verification and comparative studies

5.1. Experimental verification

5.2. Comparative studies

6. Conclusions

References

Cited by

About this article

Related Articles