Abstract
Aiming at the problems of traditional equipment fault diagnosis, such as poor real-time performance, low efficiency and strong subjectivity, a method of industrial equipment sub-health status monitoring based on big data technology was proposed. Firstly, the characteristic engineering of vibration signals is formed by preprocessing vibration signals collected by sensors located near the bearing shaft. Then, the deep residual shrinkage network DRSN was used to build the classification model. By tuning the model parameters, the optimal sub-health status identification model of industrial equipment was obtained. Finally, the accuracy, robustness and generalization of the model were verified. Experimental results show that this method has better generalization performance and can significantly improve the accuracy of industrial equipment fault diagnosis, which has important theoretical value and practical significance to solve the sub-health problems of industrial equipment.
1. Introduction
With the development of computer and artificial intelligence technology, the health status assessment technology of industrial equipment has made remarkable achievements and has been applied in many fields. For example, the predictive enhancement diagnostic system developed by relevant departments of the U.S. Navy; Diagnostic Optimization program for Army tanks; embedded diagnosis and prediction synchronization strategy [1]. Zhang et al. team [2] proposed a calculation method for the numerical expression of airborne equipment health state by combining the hidden Markov model and the improved state-conditional probability model. Deng et al. [3] evaluated heavy-duty CNC machine tools by establishing the Performance index Markov model. Deep learning model increases the number of hidden layers, which makes the model achieve good results in speech recognition, image and video classification, etc. But building a model suitable for a particular object requires a large number of data sets to train, and it takes a long time to get the right weights and biases. Zhang et al. [4] proposed a sub-health diagnosis method of rolling bearings based on deep auto-encoder-correlation vector machine network model. Pereira et al. [5] used discrete Bayesian network to extract complex structural features of high-pressure turbines of jet engines and complete its health status assessment.
2. The key technology
Deep Residual Shrinkage Network (DRSN) is a new improvement on Deep Residual Network (ResNet). It replaces the weighting of each feature channel in SENet with the soft threshold of each feature channel, and introduces the soft threshold into the network structure of ResNet as a nonlinear layer, so as to improve the learning effect of the deep learning method on the useful features of noisy data or complex data [6-7].
Deep Residual Shrinkage Network introduces a small sub-network on the basis of Deep Residual Network [8]. It consists of convolution layer, batch standardization, activation function, global mean pooling and fully connected output layer and a certain number of basic modules. Its important features are converted to larger absolute values through the convolution layer, and the features corresponding to redundant information are converted to smaller absolute values through the convolution layer. The threshold value is the boundary between them obtained by Small sub-network learning, and the input data is contracted towards zero through soft thresholding. is the input feature, is the output feature, and is represents the threshold value. The soft threshold function formula is as follows:
The derivative of soft thresholding Eq. (1) is obtained:
The derivative of the soft thresholding function is 0 or 1, through soft thresholding the features in [, ] interval is set to 0, so that other features far from 0 shrink towards 0. In this way, redundant features become zero by soft thresholding, and important features become non-zero output by soft thresholding. The main soft thresholding functions can effectively prevent “gradient disappearance” and “gradient explosion”.
There are two ways to achieve trainable feature selection, one path is to take the absolute value of all elements in the input feature graph, and then obtains a set of feature A through global mean pooling and averaging; The other path is to input the global mean-pooled features into a small fully connected network and adjust the output between 0 and 1 through the Sigmoid activation function, denoted as . The final threshold is expressed as follows:
where is the final threshold, it is a set of numbers between 0 and 1 multiplied by the average of the absolute values of the feature graph.
In deep residual shrinkage network, different samples have different thresholds. Through DRSN, unimportant features will be removed, and important features will be retained. Unimportant features will be transmitted to high-level features through the cross-layer identity path. Unimportant features will take up less and less proportion through continuous stacking of many residual modules, and finally eliminate unimportant features.
3. Industrial equipment sub-health status monitoring
3.1. Feature extraction of sub-health state of industrial equipment
Through cooperation with relevant enterprises, a large number of vibration acceleration signals, power and speed data of different parts of the shaft at the drive end, fan end and base end were obtained. Each vibration acceleration signal is collected by the channel recorder in the corresponding part of the acceleration sensor. Power and speed are measured by torque sensor/decoder, which is standard and robust. The research data includes four different states of the rotor shaft, which are normal, inner ring failure, rolling body failure and outer ring failure. As the model input is vibration signal, the data may be noisy due to the influence of frequency instability and other factors. Fourier transform, wavelet analysis and Normalization processing can de-noise all kinds of signal data.
Combined with the signal processing theory and graphics tools, a series of engineering processing is carried out on the bearing shaft signal data, which is refined into time domain feature, frequency domain feature, time frequency domain feature, time sequence feature and other multidimensional features, and preliminary feature engineering is formed. The multi-dimensional characteristics of vibration signals in different parts of bearing shaft will be obtained by feature engineering, and the number of features is relatively rich. As the rich feature dimensions and the large amount of data will affect the efficiency and performance synchronization of the model, that is the efficiency and performance of the model will be reduced by the multiple and complex input data with high redundancy. Therefore, the feature selection or dimension reduction of feature engineering should be further carried out by principal component analysis and other methods.
The specific steps are as follows:
(1) Data preprocessing. It is assumed that the set matrix is composed of n samples and m variable samples, and the influence caused by dimension and unit inconsistency of each characteristic index is eliminated through standardization, and the standard matrix is obtained. The calculation formula is as follows:
where, represents the mean value of variable , and represents the variance of variable .
(2) Calculate each eigenvalue and eigenvector. Establish the correlation matrix :
Solve the eigenvalue and the corresponding eigenvector of the matrix .
(3) Calculate variance contribution rate and cumulative variance contribution rate, and determine the number of principal components.
Calculation of variance contribution rate:
Calculation of cumulative variance contribution rate:
The number of principal components is determined by the contribution rate of cumulative variance, and the first m principal components corresponding to the contribution rate of cumulative variance exceeding 85 % are taken as the number of principal components.
(4) The principal component matrix is calculated according to the eigenvectors:
3.2. Sub-health status identification model of industrial equipment based on deep residual shrinkage network DRSN
The sub-health status identification of industrial equipment based on deep residual shrinkage network includes data partitioning, data enhancement, parameter tuning and model building.
Data partitioning: The data were divided into training set, validation set and test set by stratified sampling in a certain proportion. The training set was used to build the model, the validation set was used to build the loss function in the parameter tuning stage, and the test set was used to evaluate and compare the performance of multiple models.
Data enhancement: Industry statistics show that normal data samples are much higher than fault data samples. The imbalance of sample data will cause the problem of model overfitting. So, considering the construction of adversarial network, STMOE and other methods to deal with unbalanced data.
Model building: Despite noise reduction, data may still carry noise. In deep residual shrinkage network, when the signal with “noise” is input, the “soft thresholding” is introduced into the residual module as “shrinkage layer”, and an adaptive threshold setting method is proposed to improve the model performance. In deep residual shrinkage network, when the signal with “noise” is input, “soft thresholding” is introduced into the residual module as “shrinkage layer”, and an adaptive threshold setting method is proposed to improve the performance of the model.
Parameter tuning: The mesh search method is used to traverse the parameters of each model, and the optimal fitting degree is achieved between the model output and the actual observation data by minimizing the target loss function. To ensure that the final input model has relatively excellent performance, that is, to improve the performance of the model through parameter tuning.
4. Experimental results and analysis
This article from the characters of time domain and frequency domain, time-frequency domain features and temporal characteristics of multidimensional construct industrial equipment bearing rotor characteristics of engineering, and from the bearing axis of normal, failure of inner ring, rolling body and outer ring fault four aspects of industrial equipment of sub-health state monitoring, set up based on the depth of the residual shrinkage network DRSN sub-health state identification model of industrial equipment.
In order to verify the validity and recognition accuracy of the proposed model, we did a lot of experiments in two groups. The test data were selected from the rolling bearing fault test data of the Bearing Experimental Center of Case Western Reserve University [9]. The test bearing was SKF6205, and the signal sampling frequency was 12 KHz. One group used that the fault diameter was 0.3558 mm, the load was 0, and the speed was 1802 r/min. 100 training samples and 1000 test samples were selected for rolling bearing fault identification and verification under each running state. The confusion matrix of identification results is shown in Table 1.
Table 1Confusion matrix of rolling bearing fault detection results
Normal | 1.00 | 0.00 | 0.00 | 0.00 |
Inner ring fault | 0.00 | 0.94 | 0.05 | 0.01 |
Outer ring fault | 0.00 | 0.03 | 0.95 | 0.02 |
Rolling fault | 0.00 | 0.00 | 0.03 | 0.97 |
Normal | Inner ring fault | Outer ring fault | Rolling fault |
The other group used that the fault diameter was 0.3558mm, the load was 1 kW, and the speed was 1780 r/min. Under each running state, 60 training samples and 500 test samples were selected for rolling bearing fault detection. The confusion matrix of detection results is shown in Table 2.
Table 2Confusion matrix of rolling bearing fault detection results
Normal | 1.00 | 0.00 | 0.00 | 0.00 |
Inner ring fault | 0.00 | 0.92 | 0.06 | 0.02 |
Outer ring fault | 0.00 | 0.04 | 0.93 | 0.03 |
Rolling fault | 0.00 | 0.00 | 0.04 | 0.96 |
Normal | Inner ring fault | Outer ring fault | Rolling fault |
Experimental results show that the proposed algorithm has good detection effect on rolling bearings in different working conditions, different running states and different degrees of fault.
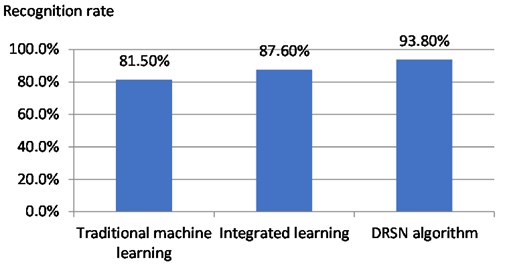
To verify the effectiveness of the proposed model, the proposed algorithm is compared with traditional machine learning and integrated learning algorithms. The index system built by model input feature engineering, the number of principal components is automatically determined from the principal components whose cumulative variance contribution rate exceeds 85 %. The output of the model is divided into four categories: normal, inner ring fault, rolling body fault and outer ring fault. It adopts DRSN algorithm based on deep residual shrinkage network to learn, and finally obtains sub-health status identification results of industrial equipment. The recognition effect is shown in Fig. 1.
Experimental results show that, among the three recognition models, the deep residual shrinkage network model proposed in this paper has the highest recognition rate of 93.8 %, and the best recognition effect, which is 4.5 % and 2.7 % higher than traditional machine learning and integrated learning, respectively. In practice, if there is any doubt about the obtained monitoring results, the sample can be added into the training set to re-learn model parameters, so as to obtain a more reasonable model.
Fig. 1Comparison of the recognition rate of the three methods
5. Conclusions
In this paper, principal component analysis method is used to extract effective features from vibration acceleration signals, power and speed data of different parts of the shaft, such as the drive end, fan end and base end. The extracted effective features are used as the input of the deep residual shrinkage network model to detect the sub-health state of industrial equipment. This method can effectively reduce the correlation between data, reduce the dimension of input data and the difficulty of machine learning model training, and realize the automatic monitoring of sub-health status of industrial equipment. Experimental results show that the proposed method has higher recognition rate and better detection effect than other methods. The further work is to improve the model on the basis of empirical analysis and apply the model to the actual sub-health monitoring of industrial equipment.
References
-
N. Hu et al., “Current situation, future and challenge of equipment health management,” National Defense Science and Technology, Vol. 36, No. 1, pp. 10–15, 2015.
-
J. Zhang, J. Zhang, and B. Cao, “Research on airborne equipment condition health assessment method based on HMM,” Computer Measurement and Control, Vol. 23, No. 2, pp. 491–493, 2015.
-
C. Deng et al., “Health state assessment of heavy CNC machine tools based on hidden Markov model,” Computer Integrated Manufacturing Systems, Vol. 19, No. 3, pp. 552–558, 2013.
-
L. Zhang et al., “Sub-health identification algorithm for rolling bearings based on fusion deep learning,” Journal of Computer Applications, Vol. 8, pp. 2224–2229, 2018.
-
J. C. Pereira, M. D. Fragoso, and M. G. Todorov, “Risk assessment using bayesian belief networks and analytic hierarchy process applicable to jet engine high pressure turbine assembly,” IFAC-PapersOnLine, Vol. 49, No. 12, pp. 133–138, 2016, https://doi.org/10.1016/j.ifacol.2016.07.563
-
M. A. Jamil, M. A. A. Khan, and S. Khanam, “Feature-based performance of SVM and KNN classifiers for diagnosis of rolling element bearing faults,” Vibroengineering Procedia, Vol. 39, pp. 36–42, Dec. 2021, https://doi.org/10.21595/vp.2021.22307
-
A. Althubaiti, F. Elasha, and J. A. Teixeira, “Fault diagnosis and health management of bearings in rotating equipment based on vibration analysis – a review,” Journal of Vibroengineering, Vol. 24, No. 1, pp. 46–74, Feb. 2022, https://doi.org/10.21595/jve.2021.22100
-
M. Zhao, S. Zhong, X. Fu, B. Tang, and M. Pecht, “Deep residual shrinkage networks for fault diagnosis,” IEEE Transactions on Industrial Informatics, Vol. 16, No. 7, pp. 4681–4690, Jul. 2020, https://doi.org/10.1109/tii.2019.2943898
-
Bearing Data Center Fault Test Data, The Case Western Reserve University Bearing Data Center, http://www.eecs.cwru.edu/laboratory/bearing/
About this article
This work was supported by the “New Generation Information Technology Innovation Project” of the Industry-University-Research Innovation Fund of China Universities (No. 2020ITA03008), Guangdong Province Colleges and Universities Key Projects (No. 2019GZDXM014).
