Abstract
It’s generally different to predict the acoustic target strength of a submarine with anechoic coatings by conventional finite element method (FEM). Parameter inversion is a common method to solve this problem. Some researchers have studied the parameter inversion about normal incidence of anechoic coatings. In this paper, the FEM of impedance tube is used to obtain acoustic reflection coefficient of anechoic coatings. Then the genetic algorithm is applied to acquire the physical parameters of viscoelastic material which is equivalent to anechoic coatings. The LMS Virtual Lab is used to construct finite element model of the anechoic coatings to validate the parameter inversion with normal incidence.
1. Introduction
As a powerful naval vessel, the submarine usually has an important characteristic of the stealth performance. One potential approach for improving the stealth performance of the submarine is to attach anechoic coatings to it. Anechoic coatings can reduce the reflection of sound waves, so it is necessary for researchers to study the acoustic scattering properties of the shell structures covered by anechoic coatings. The Finite Element Method (FEM) is most popular numerical techniques for handling acoustic computation [1, 2]. Kim established a numerical methodology based on Kirchhoff approximation to simulate the acoustic target strength (TS) of a submarine attached with anechoic coatings, and the finite element method is applied to calculate the acoustic pressure reflection coefficient [3]. Jin studied the acoustic scattering under the cylindrical wave radiation boundary of an infinite cylindrical shell with anechoic coatings based on the method of equivalent parameter inversion, and the satisfactory results had been obtained [4]. Wu analyzed the scattering characteristics of elastic spherical shells coated with locally resonant acoustic sonic materials using the T-matrix Method (TM) and the Finite Element Method (FEM) [5]. Panigrahi analyzed the acoustic scattering properties of Alberich anechoic coatings based on FEM [6]. According to the periodic boundary conditions, Hennion applied the Bloch theorem to establish the model about unit cell of Alberich anechoic coatings, and studied the resonance absorption mechanism of the cavity of the acoustic absorption materials by FEM [7, 9]. Leon researched acoustic scattering of an elastic hollow cylindrical shell of infinite length which excited by an obliquely incident plane acoustic wave, and the results of the theoretical calculation and experiment were basically consistent [7].
2. Analysis
In this paper, the considered objects are two finite length cylinder models (model A and model B), with length 1.0 m and inner diameter 1.0 m. Model A which consists of steel and Alberich anechoic coatings is composed of 2460384 nodes and 2308608 elements, model B that consists of steel and viscoelastic material is composed of 267800 nodes and 237312 elements. Fig. 1 shows the schematic diagram of them. Then the considered objects are struck by the plane wave, and the direction of the plane incident wave is along the -direction, the scattered sound pressure response at a distance of 1.0 m from acoustic center can be obtained by LMS Virtual Lab. The acoustic target strength of cylinder could be calculated by Eq. (1):
where is the reflected pressure, is the incident pressure.
Fig. 1Cross section view: a) model A, b) model B
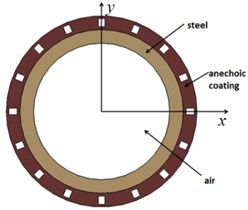
a)
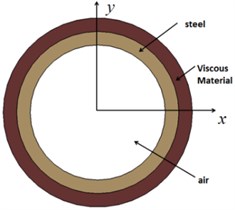
b)
The Alberich anechoic coating made of viscous materials and included specific shape holes is studied. Fig. 2 shows the physical model of Alberich anechoic coating. The geometric parameters of anechoic coatings are listed in Table 1. According to the periodicity of cavity, the model of anechoic coatings can be simplified to the unit cell to analyze the acoustic scattered properties by the Bloch theorem [6]. Therefore, the following periodic boundary conditions should be satisfied [1]:
in which the , are the displacements inanddirections, respectively.
Fig. 2Front and side view of unit cell
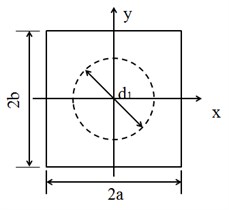
a)
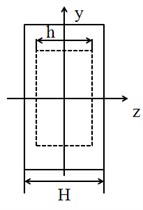
b)
Table 1Geometrics properties of anechoic coating
2 | 2 | |||
30 mm | 30 mm | 10 mm | 15 mm | 20 mm |
The impedance tube method is usually used to measure the pressure reflection coefficient about anechoic coatings. The principle of the impedance tube method is the dual hydrophone transfer function method. The acoustic signal can be divided into the incident signal and the reflection signal using dual hydrophone. The FEM can be applied to simulate the impedance tube method to obtain the pressure reflection coefficient of anechoic coatings. The reflection coefficient can be calculated by Eq. (6):
where is wavenumber, is the distance between the first hydrophone and anechoic coating, is the distance between the second hydrophone and anechoic coating, is transfer function.
As shown in Fig. 3, it’s the FE model steel structures with anechoic coatings. The material properties for the anechoic coatings and steel structures are shown in Table 2.
Fig. 3FE model for anechoic coatings to calculate the pressure reflection coefficient
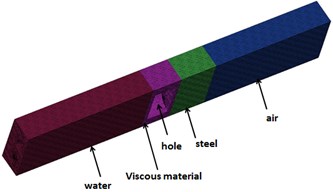
Table 2Geometrics properties of anechoic coating
Material | Young modulus | Density | Poisson ration | Loss factor | Thickness |
Viscous material | 1.4×108N/m2 | 1100 kg/m3 | 0.49 | 0.23 | 20 mm |
Steel | 2.1×1011N/m2 | 7850 kg/m3 | 0.33 | 0.001 | 25 mm |
3. The principle of equivalent parameter inversion
The Alberich anechoic coating can be regarded as a homogeneous viscoelastic material by equivalent parameter inversion. According to the principle that the original reflection coefficients () are equal to the reflection coefficients using the equivalent parameter inversion (), the genetic algorithm is applied to invert Young Modulus (), Poisson Ration () and Loss Factor () of viscoelastic material. could be acquired by using the impedance tube method based on the FEM. According to the transfer matrix method, can be calculated [10]:
where , ,…, are impedance of the layers, ,…, are the equivalent input impedance, , …, are phase displacement of acoustic wave in layers.
The genetic algorithm is a computing model simulating the natural selection of the theory of evolution of Darwin and. It can search the optimal solution within the range. The genetic algorithm toolbox in MATLAB is used to invert physical parameters and the fitness function as follows [4]:
when the is smaller than a certain value, it can be inferred that equal to and the physical parameters inverted are valid. In this paper, the certain value is 0.002.
4. Results
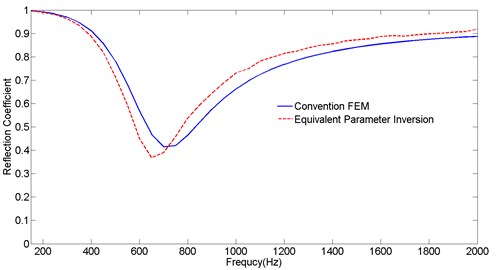
As is shown in Fig. 4, the solid line stands for the reflection coefficient that obtained from conventional FEM of anechoic coating based on impedance tube method, the dashed line represents the reflection coefficient that obtained from equivalent parameter inversion of anechoic coating based on impedance tube method. The tendency of the results of two cases is roughly consistent. Below the 720 Hz, reflection coefficient obtained from equivalent parameter inversion is smaller than it from conventional FEM. Above the 720 Hz, reflection coefficient obtained from equivalent parameter inversion is greater than it from conventional FEM. The biggest deviation between the results of two cases is 0.1, and the average deviation is smaller than 0.06.
Fig. 4Comparisons of the reflection coefficient obtained from conventional FEM and equivalent parameter inversion
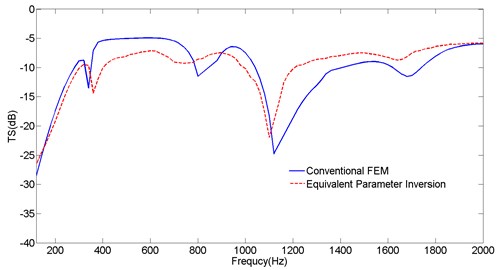
As is shown in Fig. 5, the tendency about the results of two cases is also roughly consistent. Above the 1100 Hz, the abeam acoustic target strength of cylinder obtained from equivalent parameter inversion is greater than it from conventional FEM. The biggest deviation between the results of two cases is about 5 dB, and the average difference is smaller than 2.5 dB. The deviations indicate that two target strength values are within the acceptable range, but the equivalent parameter method can reduce the computational costs and improve the computational efficiency significantly.
Fig. 5Comparisons of the TS of cylinders obtained from conventional FEM and equivalent parameter inversion
5. Conclusions
In this paper, the equivalent parameter method has been applied to simulate the target strength of finite length cylinder with anechoic coatings. This method ignores the complex acoustic structure of anechoic coatings, and the genetic algorithm has been used to invert the physical parameters (, , ) based on the principle that the the reflection coefficients obtained from conventional FEM are equal to reflection coefficients obtained from equivalent parameter inversion. The reflection coefficients are obtained by simulate impedance tube method based on FEM. Then the physical parameters have been applied to the homogeneous viscoelastic material to simulate anechoic coatings. We calculate the TS of model A and model B, and conclude that the equivalent parameter method is valid and efficient.
References
-
Yingbin Chai, Zhixiong Gong, Wei Li, Tianyun Li, Qifan Zhang, Zhihong Zou Application of smoothed finite element method to two-dimensional exterior problems of acoustic radiation. International Journal of Computational Methods, Vol. 15, Issues 1-2018, 1850029, p. 1-35.
-
Yingbin Chai, Zhixiong Gong, Wei Li, Tianyun Li, Qifan Zhang A smoothed finite element method for exterior Helmholtz equation in two dimensions. Engineering Analysis with Boundary Elements, Vol. 84, 2017, p. 237-252.
-
Hwa Muk Kim, Suk Yoon Hong Numerical simulation of submarines with anechoic coatings for acoustic target strength reduction. Naval Engineers Journal, Vol. 124, Issue 4, 2012, p. 49-58.
-
Jin Guo Liang, Yin Jian Fei, Wen Ji Hong Investigation of underwater sound scattering on a cylindrical shell coated with anechoic coatings by the finite element method based on an equivalent parameter inversion. Acta Physica Sinica, Vol. 65, Issue 1, 2016, p. 14305, (in Chinese).
-
Bei Wu, Jihong Wen Sound scattering of submerged elastic shells coated with locally resonant acoustic sonic materials. The 21st International Congress on Sound and Vibration, Beijing/China, 2014.
-
Panigrahi S. N., Jog C. S., Munjal M. L. Multi-focus design of underwater noise control linings based on finite element analysis. Applied Acoustics, Vol. 69, 2008, p. 1141-1153.
-
Hladky Hennion A.-C., Bossut R., Decarpigny J. N. Analysis of the scattering of plane acoustic wave by a periodic elastic structure using the finite element method: application to compliant tube gratings. The Journal of the Acoustical Society of America, Vol. 87, Issue 5, 1990, p. 1861-1870.
-
Hladky Hennion A.-C., Decarpigny J. N. Analysis of the scattering of a plane wave by a doubly periodic structure using the finite element method: application to Alberich anechoic coatings. The Journal of the Acoustical Society of America, Vol. 90, Issue 6, 1991, p. 3356-3367.
-
Fernand Leon, Florence Lecroq Scattering of an obliquely incident acoustic wave by an infinite hollow cylindrical shell. Journal of the Acoustical Society of America, Vol. 91, Issue 3, 1992, p. 1388.
-
Brekhovskikh L. M. Waves in Layered Media. Science Press, Beijing, 1976, (in Chinese).
