Axisymmetric scattering of a fluid spheroid illuminated by an acoustical Bessel beam

Wang, Mingsheng; Li, Wei

doi:10.21595/vp.2017.19383

Vibroengineering Procedia

Browse Procedia

Published: 17 December 2017

Check for updates

Axisymmetric scattering of a fluid spheroid illuminated by an acoustical Bessel beam

Mingsheng Wang¹

Wei Li²

¹Huazhong University of Science and Technology, Wuhan, China

²Collaborative Innovation Center for Advanced Ship and Deep-Sea Exploration (CISSE), Shanghai, China

Corresponding Author:

Wei Li

Cite the article Download PDF

Downloads 1501

Abstract

Depending on the partial wave series expression, the scattering of a fluid spheroid illuminated by a zeroth-order Bessel beam is calculated in the spherical coordinate. For a fluid spheroid, the scattering is associated with the host medium, and the immersed spheroid medium. Although spherical and cylinder fluid objects has been discussed a lot before, a prolate and oblate fluid spheroid has not been investigated deeply. In the paper, two limited boundary conditions (Neumann and Dirichlet) are presented and discussed about far-field scattering form functions. By comparing these two limited conditions, the analysis could be applied into underwater detection and acoustic tweezers, or other fields. For other fluid materials, this method could also be utilized to calculate and analyze.

1. Introduction

Over the past decades, there has been an amount of discussions about Bessel beams for optics [1], electromagnetic [2]and acoustical scattering [3]. When the incident plane wave encounters an obstacle, the diffraction, which could change the amplitude and phase of the sound wave, would occur. Taking the advantage of no-diffraction, the Bessel beam provides an attractive alternative to using the plane wave and Gaussian beams in a wealth number of applications. Furthermore, Bessel beams are self-healing; if the part of the beam is obstructed or distorted, the Bessel beam could recover after a characteristic propagation distance by itself.

Motivated by the prominent advantages of the Bessel beam, the acoustical scattering of the Bessel beam centered on the prolate and oblate spheroids could be worth investigating. Meanwhile, the incident acoustical field would be affected by the target object illuminated by the incident beam, since the incident wave would reflect, scatter, and refract off the targets’ surface. Note that because of the geometry of the prolate and oblate spheroid different from a sphere, the analytic formula would clearly lead to the inaccuracies in the prediction of the scattering and other mechanical effects of the acoustical waves.

The rigid spheroid has been investigated for a long history. However, less attention of the liquid spheroid has been gotten till 1964 when the exact solution of the diffraction of plane sound waves by an acoustically penetrable oblate spheroid was obtained for the first time [4]. And a series of reports on the scattering of waves by a penetrable prolate spheroid and the exact solution of the scattering of acoustical waves by a liquid prolate spheroid were obtained [5]. Recently, there are more papers about the approximate solution based on the discussions before [6]. Otherwise, two different methods for a plane acoustic wave from a penetrable prolate or oblate spheroid are used for the evaluation [7]. In addition, Edmundo Lavia et al. derived a computational method to calculate the exact solution for liquid spheroid which agrees with reported predicted results obtained through approximated solution for far-field and near-field regimes [8]. Based on the discussions of the scattering of the fluid spheroid, the acoustical radiation force of a fluid spheroid or a liquid-filled spherical shell could be obtained, which could benefit the application of the biomedical, drug deliver, biochemistry and other areas [9].

For a sphere, the solution approach could be obtained by the separated variable, based on an expansion of the spherical wave function. Therefore, the calculation of the prolate and oblate spheroid could be gotten through this similar way.

2. Theory

Consider a fluid spheroid immersing in the non-viscous fluid under the illumination of an acoustical monochromatic zeroth-order Bessel beam, and the incident upon a spheroid centered on its axis of wave propagation [end-on incident (Fig. 1)]. The ideal fluid surrounding the spheroid has an acoustical velocity $c_{0}$ and a density $ρ_{0}$ . The incident pressure field could be expressed as a PWSE as [10, 11]:

1

P_{i} (r, θ) = P_{0} \sum_{n = 0}^{\infty} i^{n} (2 n + 1) j_{n} (k_{0} r) P_{n} (c o s θ) P_{n} (c o s β),

where $P_{0}$ is the acoustical pressure amplitude, $j_{n}$ is the spherical Bessel function of zeroth-order of the first kind, $P_{n}$ is the Legendre function, $k_{0}$ is the wave number of the surrounding fluid, and $β$ is the half-cone angle of the Bessel beam.

Fig. 1A fluid spheroid illuminated by the zeroth-order Bessel beam along axis direction z

The complex scattered pressure field from the fluid spheroid in the surrounding non-viscous fluid could be expressed as:

2

P_{s} (r, θ) = P_{0} \sum_{n = 0}^{\infty} i^{n} (2 n + 1) A_{n} h_{n}^{(1)} (k_{0} r) P_{n} (c o s θ) P_{n} (c o s β),

where $A_{n}$ is the scattering coefficient for the host medium, and $h_{n}^{(1)}$ is the spherical Hankel function of the first kind.

Since the scattering object is composed of a fluid material, the internal pressure field inside the fluid spheroid could be expressed as:

3

P_{i n t} (r, θ) = P_{0} \sum_{n = 0}^{\infty} i^{n} (2 n + 1) B_{n} j_{n} (k_{1} r) P_{n} (c o s θ) P_{n} (c o s β),

where $B_{n}$ is the inward wave coefficient of the internal wave, $k_{1}$ is the internal wavenumber, $ρ_{1}$ is the internal density.

Since the surface shape function $S (θ)$ of the fluid spheroid is an azimuthal symmetry rotation structure and only relies on the polar angle $θ$ , its expression could be written by:

4

S (θ) = {(\frac{c o s^{2} θ}{a^{2}} + \frac{s i n^{2} θ}{b^{2}})}^{- 1 / 2},

where parameter $a$ and $b$ are the semi-axes, respectively.

The key point of this paper, is to apply continuity of the pressure and the normal component of the fluid media particle velocity at the boundary, $r = S (θ)$ , as:

5

(P_{i} + P_{s}) |_{r = S (θ)} = P_{i n t} |_{r = S (θ)},

6

\frac{1}{i ρ_{0} ω} \nabla (P_{i} + P_{s}) \cdot n |_{r = S (θ)} = \frac{1}{i ρ_{1} ω} \nabla P_{i n t} \cdot n |_{r = S (θ)},

where:

7

n = e_{r} - (\frac{1}{S (θ)}) \frac{d S (θ)}{d θ} e_{θ},

with $e_{r}$ and $e_{θ}$ denoting the outward unit vectors along the radial and polar directions, respectively.

The coefficient $A_{n}$ and $B_{n}$ included in Eq. (2) and (3) for the fluid spheroid can be obtained after substituting Eqs. (1), (2) and (3) into Eqs. (5) and (6) through Eq. (7). This procedure leads to a system of linear equations:

8

\sum_{n = 0}^{\infty} i^{n} (2 n + 1) P_{n} (c o s β) [Ψ_{n}^{p s} (θ) + A_{n} Ψ_{n}^{p s} (θ)] = \sum_{n = 0}^{\infty} i^{n} (2 n + 1) P_{n} (c o s β) [B_{n} Ψ_{n}^{p i n t} (θ)],

9

\frac{1}{i ρ_{0} ω} \sum_{n = 0}^{\infty} i^{n} (2 n + 1) P_{n} (c o s β) [Γ_{n}^{v i} (θ) + A_{n} Γ_{n}^{v s} (θ)]

= \frac{1}{i ρ_{1} ω} \sum_{n = 0}^{\infty} i^{n} (2 n + 1) P_{n} (c o s β) [B_{n} Γ_{n}^{v i n t} (θ)],

where $Ψ_{n}^{p i} (θ)$ , $Ψ_{n}^{p s} (θ)$ and $Ψ_{n}^{p i n t} (θ)$ could be given, respectively, by:

10

\{\begin{matrix} Ψ_{n}^{p i} (θ) \\ Ψ_{n}^{p s} (θ) \\ Ψ_{n}^{_{p i n t}} (θ) \end{matrix}\} = \{\begin{matrix} j_{n} (k_{0} S (θ)) \\ h_{n}^{(1)} (k_{0} S (θ)) \\ j_{n} (k_{1} S (θ)) \end{matrix}\} P_{n} (c o s θ),

where $Γ_{n}^{v i} (θ)$ , $Γ_{n}^{v s} (θ)$ and $Γ_{n}^{v i n t} (θ)$ could be given, respectively, by:

11

\{\begin{matrix} Γ_{n}^{v i} (θ) \\ Γ_{n}^{v s} (θ) \\ Γ_{n}^{v i n t} (θ) \end{matrix}\} = \{\begin{matrix} k_{0} j_{n}^{'} (k_{0} S (θ)) \\ k_{0} h_{n}^{(1)'} (k_{0} S (θ)) \\ k_{1} j_{n}^{'} (k_{1} S (θ)) \end{matrix}\} P_{n} (c o s θ) - \{\begin{matrix} j_{n} (k_{0} S (θ)) \\ h_{n}^{(1)} (k_{0} S (θ)) \\ j_{n} (k_{1} S (θ)) \end{matrix}\} \frac{1}{S (θ)^{2}} \frac{d S (θ)}{d θ} \frac{d P_{n} (c o s θ)}{d θ} .

To get rid of the influence, the variable angle $θ$ in the linear Eqs. (10) and (11), PWSEs with separable variables in Eqs. (5) and (6) could be considered. Hence, Eqs. (10) and (11) could be applied into the orthogonality condition of the Legendre functions as:

12

\frac{(2 n + 1)}{2} \int_{0}^{π} P_{n} (c o s θ) P_{n'} (c o s θ) s i n θ d θ = δ_{n, n'},

where $δ_{n, n'}$ is the Kronecker delta function.

Therefore, Eqs. (8) and (9) could be rewritten by a new system of linear equations as, respectively:

13

\sum_{n' = 0}^{\infty} [Μ_{n'}^{p i} + A_{n} Μ_{n'}^{p s}] = \sum_{n' = 0}^{\infty} [B_{n} Μ_{n'}^{p i n t}],

14

\frac{1}{i ρ_{0} ω} \sum_{n' = 0}^{\infty} [N_{n'}^{v i} + A_{n} N_{n'}^{v s}] = \frac{1}{i ρ_{1} ω} \sum_{n' = 0}^{\infty} [B_{n} N_{n'}^{v i n t}],

where:

15

\{\begin{matrix} Μ_{n'}^{p i} \\ Μ_{n'}^{p s} \\ Μ_{n'}^{p i n t} \end{matrix}\} = \sum_{n = 0}^{\infty} i^{n} (2 n + 1) P_{n} (c o s β) \int_{0}^{π} \{\begin{matrix} Ψ_{n}^{p i} (θ) \\ Ψ_{n}^{p s} (θ) \\ Ψ_{n}^{_{p i n t}} (θ) \end{matrix}\} P_{n'} (c o s θ) s i n θ d θ,

16

\{\begin{matrix} N_{n'}^{v i} \\ N_{n'}^{v s} \\ N_{n'}^{v i n t} \end{matrix}\} = \sum_{n = 0}^{\infty} i^{n} (2 n + 1) P_{n} (c o s β) \int_{0}^{π} \{\begin{matrix} Γ_{n}^{v i} (θ) \\ Γ_{n}^{v s} (θ) \\ Γ_{n}^{v i n t} (θ) \end{matrix}\} P_{n'} (c o s θ) s i n θ d θ .

The far field form function could be expressed as:

17

f_{\infty} (k r_{0}, θ, β) = \frac{2}{i k r_{0}} \sum_{n = 0}^{\infty} (2 n + 1) A_{n} P_{n} (c o s β) P_{n} (c o s θ),

where $r_{0} = m a x (a, b)$ .

3. Numerical results

Note that a water spheroid in air, the water drop could be defined as a rigid spheroid, since there is large mismatch impendence between liquid and air, which could be considered as the Neumann boundary condition, meaning the normal velocity between the fluid prolate and oblate spheroid and the host medium is zero. Based on this character, the correction of the fluid spheroid could be verified. Meanwhile, for a gas-filled spheroid in water, which is different from a water spheroid, the boundary condition could be considered as Dirichlet, meaning the pressure between the fluid prolate and oblate spheroid and the host medium is zero. Then, we will discuss about these two conditions above. The analysis will center on backscattering form function, polar scattering form function, and near-field scattering pressure. Because of the accuracy of the spherical Hankel functions with the increasing number of terms based on PWSE in this paper, the calculation method could only be applied into calculation and analysis for a prolate and oblate spheroid with a maximum aspect ratio of 3/1 or a minimum aspect ratio of 1/3.

Note that when $β =$ 0°, the incident wave corresponds to the plane wave. Consider the example that $ρ_{w a t e r} =$ 1000 kg/m³, $c_{w a t e r} =$ 1480 m/s, $ρ_{a i r} =$ 0.0014 kg/m³and $c_{a i r} =$ 340 m/s. The corresponding results of the Neumann boundary influenced by the Bessel cone are shown in Fig. 2 and Fig. 3. The 3D far-field form function directivity patterns of the Neumann boundary condition are shown in Fig. 2, with $a / b =$ 1/3, $a / b =$ 1/2, $a / b =$ 2/1, $a / b =$ 3/1 for $k b =$ 5 or $k a =$ 5. Fig. 3 shows the 3D far-field form function directivity patterns of the Dirichlet boundary condition, respectively. Also, the fluid prolate and oblate spheroid is illuminated by the zeroth-order Bessel beam (half-cone angle $β =$ 0°, $β =$ 30°, $β =$ 60°), which is correspondent to the form function for different dimensionless frequency.

By comparing the Neumann boundary condition and the Dirichlet boundary condition, there are not many differences between two conditions for the ratio $a / b =$ 1/3, 1/2 under the half-cone Bessel beam angle $β =$ 0° and $β =$ 30°. However, for $β =$ 60°, the middle scattering directivity tends towards the back for Neumann condition, which tends forward for Dirichlet condition in contrast. As observed in Fig. 2(g)-(l) and Fig. 3(g)-(l), the scattering of the fluid spheroid in the forward half part is obvious for two different conditions clearly. However, the backward depression for Neumann condition would be a little stronger than that for the Dirichlet condition. By comparing with two limited conditions for the Neumann condition and the Dirichlet condition, analysis of the scattering form function would be helpful to detect the prolate and oblate objects underwater.

Fig. 2The 3D directivity patterns of the Neumann boundary for Bessel half-cone angles β= 0°, 30° and 60° at kr0= 5: a)-c) a/b= 1/3, d)-f) a/b= 1/2, g)-i) a/b= 2/1, j)-l) a/b= 3/1

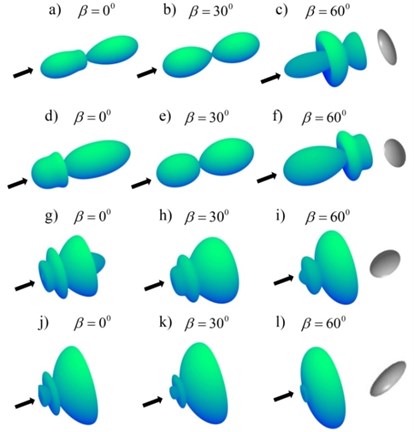
Fig. 3The 3D directivity pattern sof the Dirichlet boundary for Bessel half-cone angles β= 0°, 30° and 60° at kr0= 5: a)-c) a/b= 1/3, d)-f) a/b= 1/2, g)-i) a/b= 2/1, j)-l) a/b= 3/1

4. Conclusions

Through the discussions about the fluid spheroid illuminated by a zeroth-order Bessel beam along the axial incidence direction under two limited boundary condition, the form functions about a prolate and oblate fluid spheroid could be obtained based on the separation of variables in spherical coordinate. It is confirmed that the spherical coordinate could be applied into solution of a prolate and oblate spheroid in some degree, not only spherical fluid particles. Meanwhile, the results for the Neumann boundary condition has been obtained, hence the consequence of the Dirichlet boundary condition could also been gotten easily. Additionally, the pressure field for the incident wave and the scattering wave could be derived, and the nature could be obtained easily with particular emphasis on the half-cone angle of the Bessel beam, the dimensionless frequency, and the ratio of the spheroid. By comparing two boundary conditions, the properties of the scattering for a fluid spheroid could be distinguished easily, thus these could also be applied into practical detection underwater.

References

Turunen J., Vasara A., Friberg A. T. Holographic generation of diffraction-free beams. Applied Optics, Vol. 27, Issue 19, 1988, p. 3959-3962.

Publisher
Chen Z., Han Y., Cui Z. Scattering of Bessel beam by a conducting spherical particle with dielectric coating. Journal of Quantitative Spectroscopy and Radiative Transfer, Vol. 148, 2014, p. 197-202.

Publisher
Mitri F. G. Acoustic scattering of a high-order Bessel beam by an elastic sphere. Annals of Physics, Vol. 323, Issue 11, 2008, p. 2840-2850.

Publisher
Yeh C. The diffraction of sound waves by penetrable disks. Annalen der Physik, Vol. 468, Issues 1-2, 1964, p. 53-61.

Publisher
Yeh C. Scattering of acoustic waves by a penetrable prolate spheroid. The Journal of the Acoustical Society of America, Vol. 42, Issue 2, 1967, p. 518-521.

Publisher
Prario I. S., Gonzalez J. D., Madirolas A. A Prolate spheroidal approach for fish target strength estimation: modeling and measurements. Acta Acustica united with Acustica, Vol. 101, Issue 5, 2015, p. 928-940.

Publisher
Kotsis A. D., Roumeliotis J. A. Acoustic scattering by a penetrable spheroid. Acoustical Physics, Vol. 54, Issue 2, 2008, p. 153-167.

Publisher
González J. D., Lavia E. F., Blanc S. A computational method to calculate the exact solution for acoustic scattering by fluid spheroids. Acta Acustica united with Acustica, Vol. 102, Issue 6, 2016, p. 1061-1071.

Publisher
Yingbin Chai, Zhixiong Gong, Wei Li, Tianyun Li, Qifan Zhang, Zhihong Zou Application of smoothed finite element method to two dimensional exterior problems of acoustic radiation. International Journal of Computational Methods, 2018, https://doi.org/10.1142/S0219876218500299.

Publisher
Mitri F. G. Axisymmetric scattering of an acoustical Bessel beam by a rigid fixed spheroid. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, Vol. 62, Issue 10, 2015, p. 1809-1818.

Publisher
Li Y., Wang M., Li W. Sound Scattering of Double Concentric Elastic Spherical Shell with Multilayered Medium Cloak. Underwater Technology, Busan, 2017.

Publisher

About this article

Received

04 November 2017

Accepted

12 November 2017

Published

17 December 2017

SUBJECTS

Acoustics, noise control and engineering applications

DOI

https://doi.org/10.21595/vp.2017.19383

Keywords

bessel beam

fluid spheroid

acoustic scattering

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2021 08 11

Research progress of cavity-based acoustic energy harvester

Zhipeng Li, Huajie Zou, Jinghao Li, Hejuan Chen

Research article

2020 04 02

Numerical investigation of sound transmission loss of circular plates embedded with acoustic black hole

Xiaofei Du, Jianrun Zhang

Research article

2019 10 19

Acoustic vibration response and power generation characteristics of airborne acoustic generator system

Zhipeng Li, Hejuan Chen

Research article

2018 10 19

Low frequency acoustic energy harvesting adopting slit Helmholtz resonator

Ming Yuan, Xiaohui Wang, Zhenjun Ding

M. Wang and W. Li, “Axisymmetric scattering of a fluid spheroid illuminated by an acoustical Bessel beam,” Vibroengineering PROCEDIA, Vol. 16, pp. 91–96, Dec. 2017, https://doi.org/10.21595/vp.2017.19383

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2017.19383
UR  - https://doi.org/10.21595/vp.2017.19383
TI  - Axisymmetric scattering of a fluid spheroid illuminated by an acoustical Bessel beam
T2  - Vibroengineering PROCEDIA
AU  - Li, Wei
AU  - Wang, Mingsheng
PY  - 2017
DA  - 2017/12/17
PB  - JVE International Ltd.
SP  - 91-96
VL  - 16
SN  - 2345-0533
ER  - 

Copy Ris

Copied to clipboard!

@article{Li_2017,
	doi = {10.21595/vp.2017.19383},
	url = {https://doi.org/10.21595/vp.2017.19383},
	year = 2017,
	month = {dec},
	publisher = {{JVE} International Ltd.},
	volume = {16},
	pages = {91--96},
	author = {Wei Li and Mingsheng Wang},
	title = {Axisymmetric scattering of a fluid spheroid illuminated by an acoustical Bessel beam},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]W. Li and M. Wang, “Axisymmetric scattering of a fluid spheroid illuminated by an acoustical Bessel beam,” Vibroengineering PROCEDIA, vol. 16, pp. 91–96, Dec. 2017, doi: 10.21595/vp.2017.19383.

Copy IEEE

Copied to clipboard!

Li, Wei, and Mingsheng Wang. “Axisymmetric Scattering of a Fluid Spheroid Illuminated by an Acoustical Bessel Beam.” Vibroengineering PROCEDIA 16 (December 17, 2017): 91–96. https://doi.org/10.21595/vp.2017.19383.

Copy Chicago

Copied to clipboard!

Axisymmetric scattering of a fluid spheroid illuminated by an acoustical Bessel beam

Abstract

1. Introduction

2. Theory

3. Numerical results

4. Conclusions

References

About this article

Related Articles