Numerical study of lateral bending influence on lumbar intervertebral disc

1. Introduction

While flexion and extension of lumbar spine are performed every day multiple times, lateral bending is significantly less frequent during daily activities and therefore less researched, although lateral bending has notable influence on spine because it is primarily accomplished by movement of the spine [1].

Pure lateral bending moment is often applied to the spinal finite element models as one of the loads (together with flexion, extensions or axial rotation) in various intervertebral disc degeneration or finite element sensitivity analysis [2-4] but the influence of lateral bending on lumbar spine is not the main concern of these studies. Their results related with lateral bending show that maximum stress values in annulus fibrosus caused by lateral bending are higher compared with stress values caused by flexion, extension or axial rotation and increase even more when intervertebral disc is degenerated, on the other hand, lateral bending causes the lowest facet joint forces. Also, increased intervertebral disc degeneration reduces range of motion of lateral bending and intradiscal pressure even obtains negative values, however, failure of ligaments does not have significant influence on range of motion during lateral bending. Modeling assumptions, chosen in mentioned studies, do not allow to evaluate fluid flow paths and pressure distribution within intervertebral disc and to predict the effects of various loads on intervertebral disc nutrition.

Fluid flow within the intervertebral disc is usually evaluated by using poroelastic models of intervertebral disc, but current studies are mostly concentrated on investigation of axial compression load and diurnal cycle influence on intervertebral disc [5-6] and effects of other loads are not sufficiently researched.

The purpose of this study is to investigate the influence of lateral bending on stress values, pore pressure and fluid flow velocity of healthy and degenerated lumbar spine intervertebral discs in order to explore the possibilities to use lateral bending exercises for lumbar spine rehabilitation.

2. Methods

A three dimensional poroelastic finite element model of 35.9 mm wide and 51.9 mm long lumbar spine intervertebral disc L4-L5 with a total height of 11.4 mm was created with Comsol MultiPhysics (COMSOL Inc.) software. Model consisted of nucleus pulposus (NP), which occupied 43 % of disc volume, annulus fibrosus (AF) and 0.5 mm thick cartilaginous endplates (CEP). Composite behaviour of annulus fibrosus was represented by annulus fibrosus matrix and seven layers of annulus fibers which were modeled as tension-only elements with an inclination angle of ±24° (Fig. 1).

Fig. 1L4-L5 intervertebral disc: a) disc geometry with distinct regions of nucleus pulposus, annulus fibrosus and cartilage endplates, b) finite element model

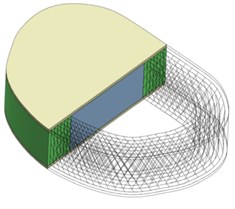
a)

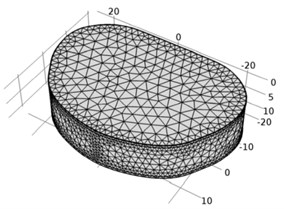
b)

Intervertebral disc was considered as fluid saturated porous media and calculation of fluid flow was based on Darcy’s generalized law. Tissues permeability was considered isotropic and strain-dependant [7]:

where $k_0$ – initial permeability; $e_0$ – initial voids ratio. Voids ratio $e$ is defined as:

where $\varphi$ – tissue porosity, which depends on volumetric strain ${\epsilon }_{vol}$:

Annulus fibers were defined with elastic modulus of 100 MPa and Poisson ratio of 0.33. Other material properties representing healthy (1st grade) and moderately degenerated (approximately 3rd grade) discs were taken from literature and are summarized in Table 1.

Intervertebral disc swelling was simulated by applying osmotic pressure gradient:

where ${\varphi }_i$ and ${\varphi }_e$ – internal and external osmotic coefficients, $R$ – universal gas constant, $T$ – absolute temperature, $c_F$ – fixed charge density, ${\gamma }_i$ and ${\gamma }_e$ – activity coefficients, $c_e$ – external salt concentration.

Fixed charge density depends on volumetric deformations and is defined as:

where $c_{F0}$ – initial fixed charge density, $n_0$ – initial fluid volume fraction, $J$ – determinant of the deformation gradient tensor.

An inferior surface of intervertebral disc was constrained in displacement. Model was validated by applying pure lateral bending moments of 1-10 Nm and checking simulation results with in vivo results given in literature [11].

In order to investigate the influence of in frontal plane constrained lateral bending move, 10° lateral bending angle was prescribed to the disk. This angle was chosen as close to the maximum failure-free lateral bending angle. During time transient analysis maximum bending value was achieved in one second time. In addition to lateral bending in frontal plane, small rotations of 2° and 5° in sagittal and transverse planes were applied to simulate situations when lateral bending move is performed unconstrained (not strictly in frontal plane) due to the physical condition of the subject.

3. Results

Fig. 2 shows pure 10° LB simulation results in frontal section view. Stress values in annulus fibrosus is significantly higher than in nucleus pulposus. Within healthy intervertebral disc the highest von Misses stress zones occur at the lateral posterior annulus rim and the maximum value is 3.15 MPa. Stress values significantly increase in annulus fibrosus of degenerated intervertebral disc and reach value of 9.12 MPa. However, there are no significant changes of stress values within nucleus pulposus of healthy and degenerated discs. Disc degeneration also increases absolute values of pore pressure and pressure distribution between nucleus pulposus and annulus fibrosus becomes less smooth. Calculations show that fluid flow velocity in degenerated disc also increases, but higher fluid velocity value in degenerated disc does not mean that disc degeneration has any beneficial effects. Due to the reason that exact lateral bending angle was prescribed in this study instead of lateral bending moments, it could be assumed that reactions and strain values of degenerated disc are higher, as degeneration tends to increase a stiffness of intervertebral disc, so that the same bending angle could induce critical stress values and increase risk of failure.

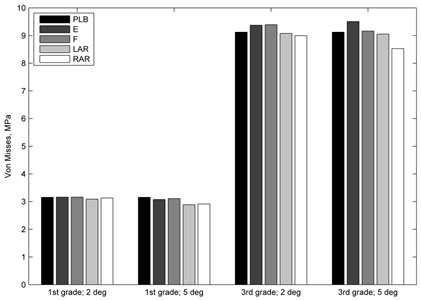
The results of combined loading modelling (Fig. 3) reveal that additional 2° flexion, extension or axial rotation moves lead to only minor changes in stress values of healthy annulus, while additional 5° moves change maximal stress values more noticeably. It was calculated that 2° additional flexion and extension moves cause a minor increase in annulus fibrosus stress values, while 2° axial rotations reduce the stress level of pure lateral bending. Additional loads of 5° reduce maximal stress values in all four combined loading cases. Both 2° and 5° additional flexion and extension moves increase stress values in moderately degenerated annulus, while 2° and 5° axial rotations reduce stress values compared with pure lateral bending.

Fig. 2Results of pure 10° lateral bending in a) healthy; b) degenerated intervertebral discs. Frontal plane section view

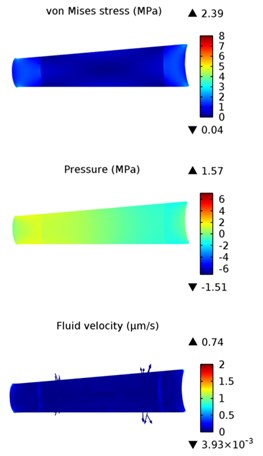
a) Health disc

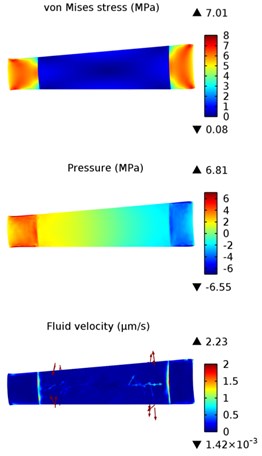
b) Degenerated disc

Fig. 3Von Misses stress values induced by pure lateral bending and additional loads of 2° and 5° in healthy (1st grade) and degenerated (3rd grade) discs: PBL – pure 10° lateral bending, E – lateral bending + extension; F – lateral bending + flexion; LAR and RAR – lateral bending + axial rotation to the left or right

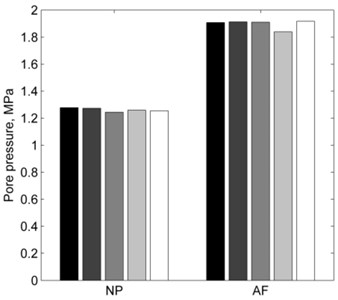
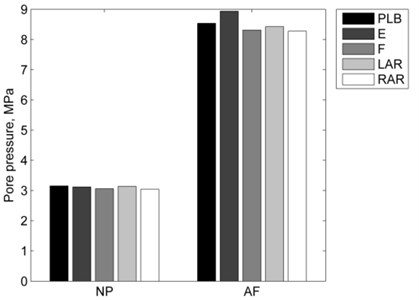
Combined loading and disc degeneration also have the influence on intervertebral disc pore pressure (Fig. 4). Nucleus pulposus pore pressure is almost 2.5 times higher and annulus fibrosus pore pressure is almost 4.5 times higher in degenerated disc. While changes in the nucleus pulposus pore pressure due to additional rotations are insignificant in both – healthy and degenerated discs, changes in annulus fibrosus are more noticeable and their patterns are different for healthy and degenerated discs. Left axial rotation has the most influence on healthy disc annulus fibrosus pore pressure, while additional extension affects pore pressure of degenerated annulus fibrosus the most.

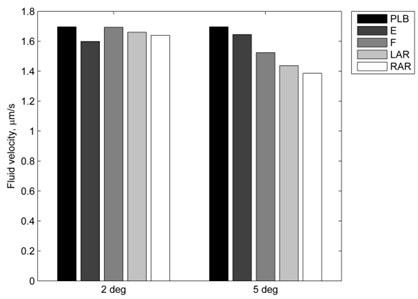
Combined loading also influences fluid flow velocity through the intervertebral disc (Fig. 5). Fluid velocity within healthy nucleus pulposus is reduced by all 2° and 5° additional moves compared with pure lateral bending values. 2° additional extension move has the most significant influence of all 2° moves while 5° additional rotations reduce nucleus pulposus fluid velocity the most. The highest fluid flow velocity is at the boundaries of an intervertebral disc and at the circumferential area between nucleus pulposus and annulus fibrosus.

Fig. 4Pore pressure comparison between loading cases: a) healthy intervertebral disc; b) degenerated intervertebral disc (PBL – pure 10° lateral bending, E – lateral bending + 2° extension; F – lateral bending + 2° flexion; LAR and RAR – lateral bending + 2° axial rotation to the left or right)

a)

b)

Fig. 5Fluid velocity in healthy nucleus pulposus: PBL – pure 10° lateral bending, E – lateral bending + extension; F – lateral bending + flexion; LAR and RAR – lateral bending + axial rotation to the left or right

4. Conclusions

The results of lateral bending of poroelastic intervertebral disc show that stress values in intervertebral disc increase when more degenerated intervertebral disc is bent, and this agrees with results of the study where nucleus pulposus was modeled as fluid filled cavity and annulus fibrosus matrix was assumed hyperelastic [2], so various intervertebral disc modeling methods present similar results of lateral bending induced stress values of intervertebral disc.

Disc degeneration also increases pore pressure of intervertebral disc, especially within annulus fibrosus, and this could lead to intervertebral disc disorders such as disk herniation.

Due to significant disc degeneration influence, the condition of patient’s spine should be evaluated before defining an intensity of lateral bending exercise. While combined loading simulations do not show any significant changes in annulus stress values and more comprehensive study is necessary to define exact relationships between combination of different loads and their induced stress, obtained results could imply that additional flexion and extension loads are more dangerous than axial rotations and could induce higher annulus fibrosus stresses than pure lateral bending.

Fluid flow velocity reduced during combined loading could suggests that in frontal plane constrained lateral bending exercise is more beneficial than other moves in order to achieve better nutrition of intervertebral disc.