Abstract
Compared with finite element method (FEA) and statistical energy method (SEA), the energy finite element method (EFEA) is a promising and more suitable method to predict the high-frequency vibration response and radiated noise of mechanical structures, due to its advantages of both computational efficiency and ability to get detail information. In recent years, researchers have made great progress in EFEA, due to the urgency of engineering application. This paper aims to comprehensively summarize historical and latest development of energy finite element analysis from two aspects of theory and engineering, to furtherly promote its application in the engineering field. Firstly, the development history of EFEA in basic structures is summarized, and the theoretical development direction of energy finite element in recent years is further analyzed. After that, the application of EFEA in aerospace, ship and vehicle engineering are summarized. Finally, the problems that need to be furtherly studied in EFEA are presented, and it is pointed out that it is an urgent research work to continue to improve the energy finite element analysis theory and software and apply it to engineering.
Highlights
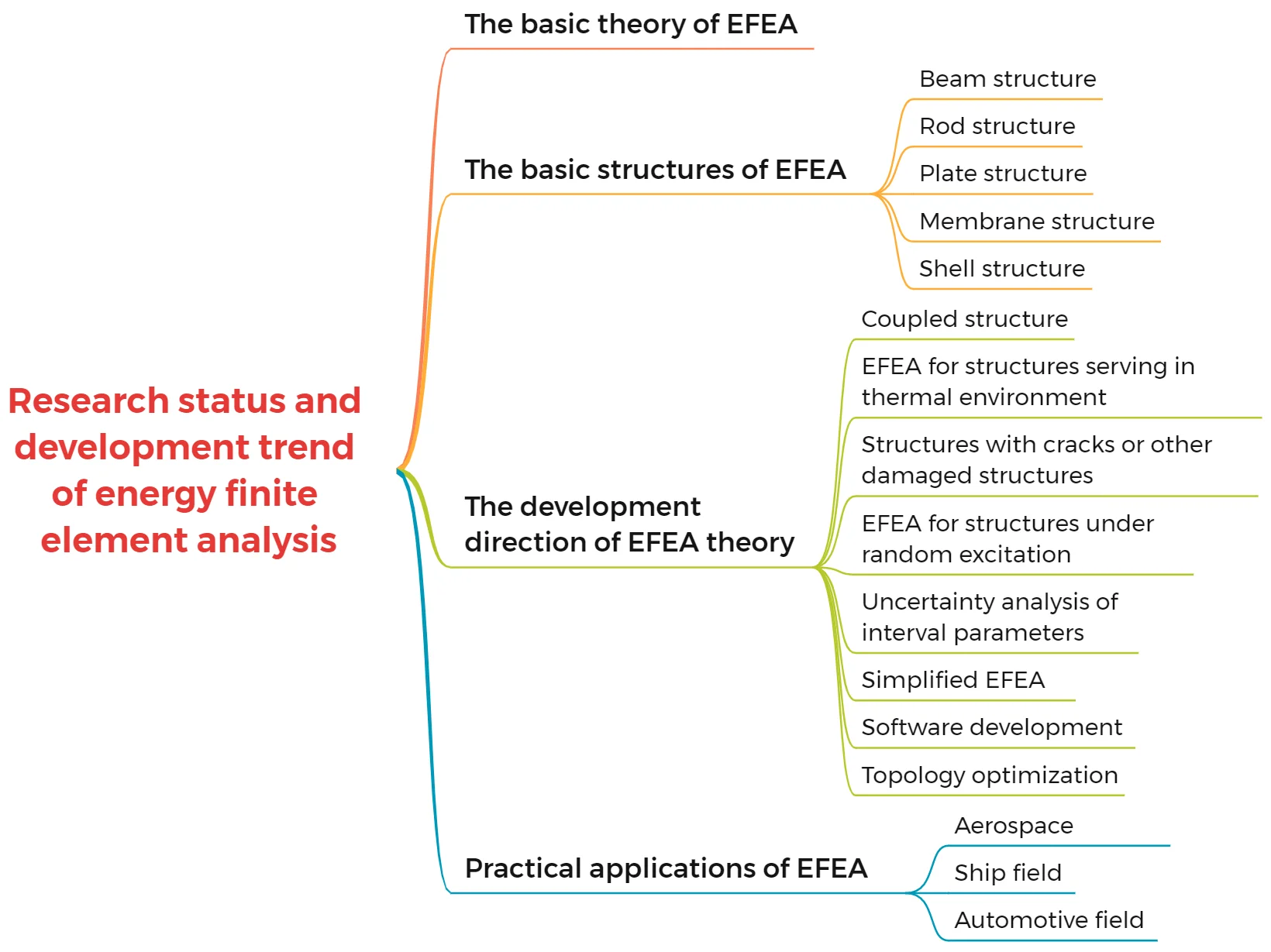
- Development history of energy finite element analysis for beam, plate, rod, membrane, shell was reviewed. It is a foundation for appling the EFEA to structure design in engineering.
- New research branches of energy finite element analysis are summarized and analyzed. It includes coupled structures, structures serving in thermal environment, structures with cracks or other damaged structures, structures under random excitation, uncertainty analysis of interval parameters, simplified EFEA, the progress of EFEA in software development, topology optimization.
- The future research work worthing to be done was presented.
1. Introduction
With the development of science and technology, the vehicles have gradually developed toward the direction of high speed and lightweight, so in the mechanical design stage of the vehicles, in addition to the low-frequency dynamic response prediction, the medium and high-frequency vibration of the structure has to be considered. Therefore, the vibration response analysis of the mechanical structure in the high frequency domain is also an important problem that must be solved in the structural design of modern vehicles. Numerical analysis is usually used to solve complex structural vibration problems. Finite Element Analysis (FEA) is a powerful tool to study the vibration response of a structure. It discretizes the complex structures into several elements and discretizes the governing equations according to the element nodes to form matrix equations and solve them in combination with boundary conditions. However, in the middle and high-frequency vibration analysis, it is necessary to divide more and finer meshes to reflect the real vibration response results of the structure, so it requires more time and cost. In the case of large scale structures, the number of meshes required is too large, often the time cost is usually unacceptable, and beyond what existing computers can afford [1]. On the other hand, in the low-frequency band, the wavelength in the system is large, and the response is not sensitive to the parameter perturbation, so the finite element method can effectively predict the low-frequency response. At high frequencies, the wavelength is short, and with the increase of the analysis frequency, the energy density of the vibrating structure tends to be uniform, so it is generally difficult to accurately predict the high-frequency vibration response characteristics of complex structures by the finite element method. Since mid-high frequency, especially high frequency, tends to describe the response in the average sense, Statistical Energy Analysis (SEA) can be widely used in mid-high frequency analysis. The statistical energy method is based on sub-structure division, regards energy as a variable in the sub-structure, establishes an energy equation, and obtains the energy response of each sub-structure, avoiding the large amount of calculation caused by medium and high frequencies. However, this method can only reflect the average energy level of the substructure, and cannot accurately describe the detail information of the energy response within the substructure.
EFEA takes the time-space average energy density as the variable of the governing differential equation and then uses the finite element method to solve the governing differential equation so that the energy density of all nodes in the structure can be obtained, the energy finite element analysis is usually used to analyze the vibration and noise problems of medium and high-frequency structures. This method can not only overcome the upper-frequency limit problem of the finite element method due to the dense structural modes in the middle and high-frequency analysis but also avoid the problem that the statistical energy method loses the spatial variable information of the substructure and cannot accurately describe the energy response in the substructure. The energy finite element analysis can use fewer elements to analyze large scale and complex structures and obtain the response results in a shorter time, which greatly shortens the product design time [2].
This paper traces the development history of the energy finite element analysis and analyzes the engineering application fields of EFEA in recent years, as well as the theoretical research direction of EFEA, which has a certain role in promoting the wide application and theoretical maturity of the energy finite element analysis.
2. The basic theory of EFEA
In EFEA, the variable of the governing differential equation is the time and space-averaged energy density, and the energy density is obtained by solving this equation by using the finite element method. The basic theory of EFEA for an isotropic plate will be introduced as follow.
When the isotropic thin plate structure is subjected to harmonic excitation, the equation of motion of the bending wave in the plate is as follow:
where is the thickness of the plate, is the density of the plate material, is the hysteretic damping coefficient, is the harmonic excitation of the isotropic thin plate, and is the Bending stiffness, , is the Young’s modulus of the material, is Poisson’s ratio, is the Laplace operator whose expression is as follow:
Using the general solution form of Eq. (1), the expressions of energy density and intensity can be obtained, and the relationship between the time-space average energy density and intensity can be obtained by further observation as follows:
The wave group velocity in Eq. (3) is as follow:
According to the conservation of energy is as follow [3]:
where, represents the input of energy in the system; represents the dissipation of energy in the system. The energy density equation can be obtained:
where, is the input power. According to the Galerkin weighted residual method, the above equation is discretized, and the equation matrix form of the energy finite element analysis is obtained:
In Eq. (7):
Solving Eq. (7), the energy density at each node can be obtained.
3. The development history of EFEA for the basic structures
EFEA originated from the study of energy flow. In 1975, Belov and Rybak [4] first proposed the Power Flow Analysis (PFA) method, which uses differential equations in the form of heat conduction to describe the energy flow distribution in a vibrating structure. In 1977, Belov [5] et al. on the premise of introducing the wave theory, assumed that the waves generated by the structural vibration were uncorrelated, and the energies of several waves could be superimposed on each other without affecting each other and used differential equations to analyze flexural and longitudinal wave energy flow transfer in beam-slab structures. In 1983, Butlitskaya [6] et al. studied the noise and vibration problems of ventilation duct structures using differential equations in the form of heat conduction developed by Belov and Rybak (1979). At that time, Belov and Rybak’s research was not based on strict continuum mechanics, but only theoretically applied the structural heat conduction method to structural vibration problems.
The basic structure refers to the structure without the sudden change of geometric parameters and material parameters. In the process of energy finite element analysis of the basic structure, the energy density governing equation of the corresponding basic structure only needs to be derived, and the energy density governing equation can be solved by finite element method, without solving the problem of energy density mutation at the coupling. Basic structures, such as ordinary bars, beams, plates, membranes, shells, etc.
3.1. Development of EFEA for beam structures
In 1989, Nefske and Sung [7] obtained the energy density governing equation of beam structures from the intrinsic relationship between energy flow and energy density, the functional expression of power loss and energy density, and the relationship between power input and output in micro-elements, and compared with the traditional modal analysis, it proves that the method is simpler. However, some of the assumptions they propose differ from traditional wave mechanics. In 1990, Burrell et al. [8] used the finite element analysis to solve the energy flow governing equation established by Nefske and Sung, then compared it with the traditional modal analysis method. The results show that the finite element analysis is faster to solve the energy flow control equation. However, the stationarity of the response results cannot be explained by the above method. In 1992, Wohlever et al. [9] artificially proved that the power flow method is theoretically established. Through the wave solution of the equation of motion and the basic dynamic theory, the relationship between the structural energy (kinetic energy and potential energy) and the intensity was established, and the energy density was deduced. The governing equation taking the energy density as variable for a bar-beam structure is as follow:
where, . In the same year, Lase [10] proposed that the boundary conditions were represented by energy flow, and the vibration response of each position on the beam structure was represented by the magnitude of the energy density. In 2006, Park et al. [11] used the energy flow model to analyze the influence of the moment of inertia and shear deformation, deduced and solved the energy density governing equation of the Timoshenko beam, and obtained the energy density distribution on the Timoshenko beam. A functionally graded material is a heterogeneous composite material whose overall properties show gradient changes by continuously changing the distribution of component materials [12]. In 2008, Yang et al. [13] based on the classical Euler beam theory, studied the vibrational properties of FGM beam structures with different boundary conditions. In 2013, Zhang M. et al. [14] proposed energy finite element analysis for structures with random parameters. They used the expectation and variance formulas of continuous random variables and the traditional energy finite element analysis to obtain the response of the beam structure at any position in the random parameter system. Variance, mean and analytical solutions of the energy density response for this structure were obtained, and compared to Monte Carlo simulation results for the energy density modal solution. In 2016, Deng H. et al. [15] analyzed the theoretical model of the functionally graded material Timoshenko beam based on the theory of dynamics and variable substitution. In 2018, Lin Z. L. et al. [16] introduced a formula to solve the energy density discontinuity problem at the junction with stepped thickness beams. In addition, several design examples at different frequencies and damping loss factors were used to verify the feasibility of the EFEA. Wang D. et al. [17] used EFEA to obtain the energy flow of the functionally graded material beam structure and obtained the energy distribution of the coupled functionally graded material beam structure by solving the energy density and energy flow in the structure. In March, 2021, Liu N. [18] established the energy balance equation of functionally graded beam based on Euler-Bernoulli beam theory by using the characteristics of functionally graded structure, and combined with Galerkin weighted residual method, established the EFEA model of functionally graded beam structure. In May, Liu Z. H. et al. established the energy flow of thermal gradient beams to analyze the temperature difference between the inner and outer surfaces of aerospace structures caused by aerodynamic heating during high-speed flight, resulting in the dynamic response of beams containing temperature gradients under high-frequency excitation [19]. In these works, researchers investigate different types of beam structures and provide a theoretical basis for analyzing the vibration behaviour of complex structures including beams using EFEA. In September, Chen X. F. [20] and others deduced the wave number, energy density and power of composite laminated beams based on Timoshenko beam theory. The relationship between energy density and power was obtained by time average and local space average methods, and the energy density equation of symmetric laminated beams was established. According to the Galerkin weighted residual method in the finite element method, the equation is solved, and the energy finite element model is obtained. By comparing the EFEM solution and WPA solution of the density distribution of laminated beams through an example, the EFEM solution can accurately predict the energy density distribution of symmetric laminated beams under medium and high frequency excitation. In 2022, Miaoxia Xie et al. established the energy flow model of the tapered beam with variable thickness, derived the equivalent wave group velocity in the tapered beam using acoustic approximation method, and numerically solved the energy density governing equation of the tapered beam. This research will promote the application of energy finite element method to variable thickness structures [21].
3.2. Development of EFEA for rod structures
In 1990, Jezequel and Lase [22] used a method similar to Sung [7] to establish the energy density governing equation for the longitudinal vibrating rod structure and realized the spatial distribution of energy density to represent the entire response of the longitudinal vibrating rod. In 2004, Sun L P derived the energy density governing equation of the rod structure under simple harmonic excitation, obtained a simplified solution of the equation, and verified the similarity between the energy flow and heat flow of the vibration-noise structure proposed by Nefske and Sung [23]:
3.3. Development of EFEA for plate structures
In 1992, Bouthier O. M. and Bernhard R. J. [24] derived the governing equation of the energy density of the thin plate structure. They solved the governing equation of the energy density of the plate structure by the finite element analysis, and found that the maximum energy density is at the excitation position of the plate structure. With the distance from the excitation position, its energy density gradually decreases, and the energy flow spreads around the excitation position. In 1995, Bouthier O. M. and Bernhard J. R. [25] derived approximate energy models for infinite and finite plates using the relationship between energy balance loss coefficients, damping models, and approximate energy transfer models. Eq. (14) is the energy density governing equation of the plate structure:
In 2008, Yan [26] developed a new EFEA model for composite laminates, and verified the results of the EFEA equation by comparing it with the results of the dense mesh finite element model. The governing equation for the composite laminate is:
where, is a function of the wave propagation angle :
In the same year, Moraveji [27] applied the energy finite element analysis to the trim panel structure. In 2014, Zhu W. H. [28] decoupled the in-plane motion and out-of-plane motion of the thin-plate structure from the thin-plate theory, established a finite element energy flow model of these two motions, and obtained the bending factor of the plate structure through the energy balance equation. In 2019, He L. et al. [29] from Xi’an Jiaotong University discretized the energy density governing equation of anisotropic plate structures, deduced the energy finite element equation for anisotropic plate structures, then used numerical examples to compare EFEA with traditional models. The calculation results of the state method were compared to verify the correctness of the energy density governing equation of the orthotropic thin plate structure. After, He L. et al. solved the energy finite element equation to obtain the structural sound intensity, and finally analyzed the influence of local damping distribution at different positions on vibrational energy transfer characteristics of orthotropic thin-plate structures. In 2021, based on thin plate theory, Liu N [18] established the relationship between sound intensity and energy density after Spatio-temporal averaging processing and far-field approximation assumption, and then deduced the governing equation of energy density for functionally gradient plates. Then, in order to establish the high frequency vibration analysis method of the functionally gradient plate structure in contact with the average flow by EFEA, the fluid dynamic pressure model was established by using the velocity potential function and Bernoulli equation, and the governing equation of energy density was derived by considering the bending wave number of the plate in different directions along the bending wave and the average flow. In 2022, Zhidong Cai [30] deduced the energy equation of the in-plane free vibration of rectangular laminated plates based on the energy method solution framework, and then established the numerical analysis model of rectangular laminated plates on the premise that Legendre polynomials and artificial spring technology represent the allowable function of structural displacement and boundary conditions. Then the correctness of this method is verified by comparing the solution results with the finite element results.
3.4. Development of EFEA for membrane structures
In 1990, Bouthier O. M. studied the relationship between the spatially averaged energy density and the structural strength of membrane structures. He assumed that when the damping in the structure is small, the strength of the structure is proportional to the gradient of the spatially averaged energy density [31]. In 1995, Bouthier O. M. and Bernhard J. R. [32] explored the corresponding power flow method for two-dimensional structures based on previous studies. They considered the tension factor in the 2D film and derived the governing equation of the energy density for the 2D film. In 2022, Kun Wang et al. [33] proposed an analytical formula for the average energy of large-scale spatial membranes with deterministic parameters based on the Green's kernel of vibrating membranes and using the average free path to describe the propagation distance of energy waves, which is applicable to membranes of various shapes. After that, the vibration energy formula of large membrane with random parameters is developed and its correctness is verified by the accurate energy response of the traditional displacement scheme. The vibration analysis from the energy angle is further promoted.
3.5. Development of EFEA for shell structures
In 2008, Miaoxia Xie [34] predicted the energy density distribution of a cylindrical shell under axisymmetric loads based on the thin shell theory. In the same year, Dong H. [35] derived the axial and hoop displacement equations based on the motion equation of the free vibration of the cylindrical shell, and then from the relationship between energy density and strength, the energy density governing equation of the cylindrical shell structure is constructed. In 2014, Kong [36] obtained the governing equation of out-of-plane vibrational energy for thin shells and gave the energy density distribution of hyperbolic shells.
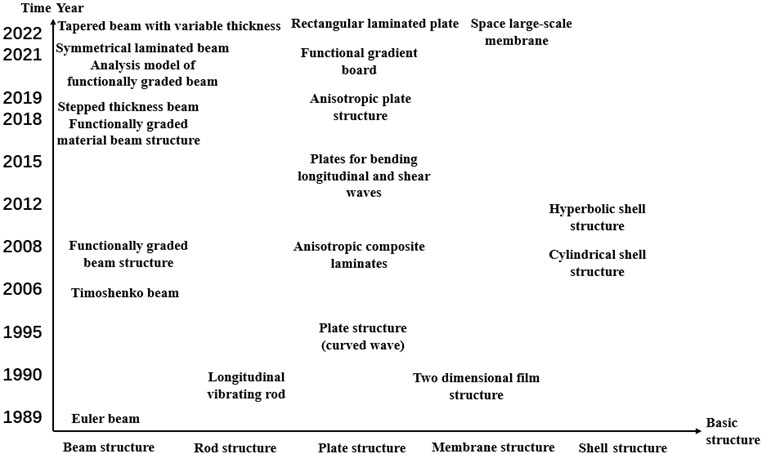
To sum up, the development overview of energy finite element analysis for basic structures such as rods, beams, membranes, plates, and shells is shown in Fig. 1. It can be seen from the figure that the energy finite element analysis of the basic structure kept to develop in the past 10 years.
Fig. 1Development of energy finite analysis for the basic structure
4. The development direction of EFEA theory
With the development of the energy finite element analysis theory of basic structures, the energy finite element analysis has attracted the attention of many scholars. According to the documents obtained from the SCI database and CNKI, the author summarizes the number of papers on the energy finite element analysis over the years (as shown in Fig. 2).
Fig. 2The numbers of paper on EFEA over years
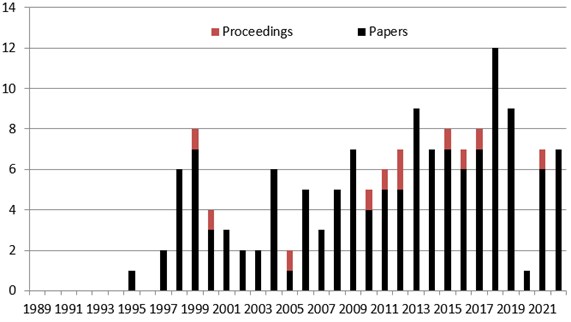
It can be seen from the number of works of literature on the energy finite element analysis over the years that from 1995 to 2022, the energy finite element analysis has received more and more attention from scholars.
Based on the development of energy finite element analysis for the basic structural, the energy finite element analysis has also achieved remarkable results in other branches. Such as the field of acoustic-vibration coupling, vibration analysis of cracks and other damaged structures, prediction of vibration response under thermal environment, prediction of vibration response under random excitation, topology optimization, and simplified energy finite element and energy finite element software development, etc.
4.1. EFEA for coupled structures (structure-structure coupled structure and acoustic-vibration coupled structure)
A coupled structure is defined as a structure where there is a sudden change in geometry or material property, such as a combined structure in which two substructures with different thicknesses are connected, or two substructures with different material properties are connected, it also includes vibration-acoustic coupling problems. At the joint of the coupling structure, due to the discontinuous energy density, the energy transfer coefficient at the joint needs to be studied, and the energy transfer relationship needs to be reflected in the overall stiffness matrix. This is the difference between the energy finite element analysis and the finite element analysis in solving, and it is also one of the problems that need to be solved in the theoretical research and engineering practice research of the energy finite element analysis.
The research on structure-structure coupling has always been a problem that must solve for practical engineering applications. In 1974, Nikiforov [37, 38] conducted researches on the energy flow of stiffened rib structures and established a second-order partial differential equation with energy density as a variable. In 1980, Buvailo and Ionov [39] used the finite element analysis to calculate the partial differential equation established by Nikiforov but did not involve the coupling problem at the joint. In 1998, Cho P. E. and Bernhard R. J. [40] first proposed to apply the energy finite element analysis to the coupling structure. They creatively used the virtual element for the coupling boundary, that is, the node where the two structures contacted at the joint were disassembled into two nodes, which effectively solves the problem caused by the discontinuous energy density at the joint during the numerical solution. In 2013, Niu J. and Li K. [41] considered three kinds of waves existing in the plate and analyzed the energy flow and energy density distribution of the “N” type plate coupled at any angle. In 2015, Jiang M. S. [42] used triangular elements to divide the grid for any plate structure, and obtained the energy density distribution and energy flow distribution of any plate and its coupled structure. In 2016, Liu Z. H. [43] used the energy finite element analysis to analyze the dynamics of the multi-plate coupled structure and obtained the energy transfer coefficient at the coupling and the overall finite element equation of the multi-plate coupled structure. The constructed analytical model can be used to predict energy densities of in-plane and bending waves for multi-plate coupled structures. In 2017, Liu Z. H. [44] also used the method of establishing the corresponding energy density vector with triangular and quadrilateral elements and applied it to the energy response prediction of closed cavity structure and the energy prediction of the coupling plate of the carriage. Zeng J. et al. [45] introduced and extended the hybrid energy finite element analysis (Hybrid-EFEM) to general coupling conditions. In the same year, Ge Y. [46] et al. studied the influence of different coupling angles, different plate thicknesses and other factors on the energy reflection and transmission coefficient in the plate. In 2018, EFEA was successfully applied to linear and “L” joint sandwich structures containing mass blocks to obtain the energy densities of the structures at different frequencies by Xu P. F. [47] et al. In the same year, Liu Z. [48] et al. considered that the power transfer coefficient in traditional EFEA could not capture the filtering effect, and can only provide accurate predictions when the damping effect is weak, then inspired by the power coupling concept of statistical energy analysis, an alternative and improved method for EFEA coupled structures (iEFEA) is proposed, that is, using coupling loss factors and considering direct alternative method of wave field. In 2018, He L. [49] et al. calculated the energy density of flexural waves of thin-plate structures through EFEA, and compared it with the statistical energy method to judge its accuracy. In 2021, Liu N. [18] simplified the stiffened plate structure into a plate-beam coupling structure, deduced the energy transfer coefficient by using the continuous principle of energy flow, and solved the model by MATLAB programming. In addition, when calculating the energy transfer coefficient at the coupling of the stiffeners with the presence of the fluid load effect and the stiffeners, the influence of the fluid at the coupling of the plate and the stiffeners on the energy transfer coefficient is analyzed and discussed.
Another structure-structure coupling method is for a combined structure that includes both rigid components and flexible components. Rigid components are calculated by the finite element method, and flexible components are calculated by the EFEA. Compatibility conditions between the two components need to be established where the rigid and flexible components are connected.
In the field of acoustic vibration coupling, EFEA also has many applications. In 1996, Bitsie [50] used the EFEA to analyze the plate-acoustic coupling structure. From 2005 to 2010, Zhang W. G. and Raveendra S. T. [51-55] and others conducted a series of analyses of the acoustic-vibration coupling structure using EFEA. They analyzed the ship structure with both structural elements and acoustic space by using EFEA. In 2006, Raymond F and Boroditsky L. et al. [56] expounded on the advantages and disadvantages of EFEA and SEA Vibro-Acoustic Models, and further emphasized the respective characteristics of SEA and EFEA in predicting the habitable noise of surface ship platforms. It has been shown that EFEA has outstanding capabilities in terms of detailed analysis of the acoustic environment and surface response under different excitation sources. From 2005 to 2007, Manning, Hong [57-59], and others used the EFEA to analyze the acoustic and vibration characteristics of vehicles. From 2008 to 2009, Lima D. et al. [60, 61] applied EFEA in the study of the acoustic-vibration coupling problem of aircraft structures. In 2010, Xie M. X. et al. [62] used plate shell elements to simulate the high-frequency structure-acoustic coupling characteristics of aircraft cabins and used a new method to obtain the detailed distribution of the flexural wave energy density on the cabin surface and the interior space of the cabin under the coupling conditions. In 2017, Wang S. [63] conducted a noise prediction study on a car and predicted the acoustic-vibration response of the interior cavity and plate elements of the car. In 2019, Wang H. Z. [64] and others established an EFEA model of an instrument cabin and predicted the acoustic and vibration environment of an instrument cabin structure. Finally, they compared EFEA and SEA with the test results and found that EFEA can predict results in more detail and match actual results. In 2021, Li A. [65] conducted a detailed analysis of the energy transfer coefficient of the one-dimensional coupled beam structure, then based on the energy transfer analysis of the two-dimensional isotropic plate-shell coupled structure, based on the typic laminate theory, solved the composite structure energy transfer properties of material laminate-beam coupled systems. In 2022, Zhu L. J. et al. [66] proposed an analytical model of the dynamics of a floating foundation vibration reduction system supported by elastic components through Lagrange equation of motion based on the energy method and combined with six-DOF rigid body small deformation mechanics, and deduced the mass matrix, stiffness matrix and damping matrix of the system. In March, Liu Jun [67] used the finite element method, energy method and Hamilton variational principle to establish the multi field coupling nonlinear vibration characteristics of the lifting pipe with longitudinal vibration and other nonlinear factors for the vibration of the lifting pipe in deep-sea mining, and studied the vibration response of different positions of the pipe string, analyzed the impact of the mass of the buffer station on the vibration response of the lifting pipe, and finally discussed the vibration response and nonlinear behaviour of the lifting pipe under different wave parameters. In May, Li A. [68] solved the wave-number curve based on the displacement assumption of wave method and Langley proposed the wave stiffness matrix method to solve the energy transfer coefficient of the orthogonal anisotropic laminate and shell coupled structure, and improved the theory related to high-frequency vibration of laminate and shell coupled structure.
4.2. EFEA for structures serving in thermal environment
Uneven temperature distribution or temperature change will cause thermal stress inside the structure, which will cause axial force in the beam structure, and the temperature will also change the material properties, which makes the EFEA for structures serving in the thermal environment is difficult. In 2014, Zhang W. et al. [69] considered that the temperature would indirectly change the wavenumber and group velocity, thereby affecting the energy governing equation. They used the energy flow analysis to predict the vibration response of the beam structure in the thermal field. In 2015, Wang D. et al. [70] studied the high-frequency energy response of two-dimensional plate structures and coupled plates in thermal environments. It has been shown that temperature distribution not only change the film stress state and temperature-dependent material properties but also affect the energy reflection coefficient and energy transmission coefficient of the coupled structure. In the same year, Wang D. proposed a method similar to EFEA based on a homogeneous thermal environment and analyzed the energy response of the coupled plate in a non-homogeneous thermal environment. In 2018, Chen Z. L. et al. [71] developed an EFEA to predict the high-frequency vibration response of beams with axial force, which verified the feasibility and correctness of EFEA.
4.3. EFEA for structures with cracks or other damaged structures
Cracks or various damages will reduce the structural stiffness and increase the damping, which will affect the propagation of vibration waves and the distribution of vibration energy. According to the calculation results, when the Young’s modulus value is lower and the damping value is higher, the difference of energy flow in the damaged part will obviously increase, and the sudden change of energy density will occur at the node of the damaged element. Therefore, the damaged parts in the structure can be identified according to the calculation results of the energy finite element analysis. In 2012, Xu F. H. [72] predicted the vibration response of beam and plate structures with cracks based on the EFEA then analyzed the influence of the crack location and its size on the energy density distribution. In 2017, Wang D. et al. [73] used the EFEA to calculate the vibration response of the plate and coupled plate structures with crack and compared it with the results of the finite element analysis to verify the accuracy of the EFEA. In 2019, Shang B. Y. et al. [74] used the EFEA to predict the vibration response of the liquid-filled pipeline and tried to identify the damaged part through the two indicators of energy density change and energy flow difference.
These studies provided a reference for using the EFEA to predict the vibration response of engineering structures with cracks and other damage and to identify the damaged parts of the engineering structure.
4.4. EFEA for structures under random excitation
In 2009, You J. et al. [75] studied the energy and energy flow distribution of beam structures subjected to several uncorrelated random excitations based on the energy flow method. In 2010, You J. [76-78] studied the energy density and energy flow distribution of the “L”-shaped coupling plate under random excitation, analyzed the influence of the correlation between random excitations on it, and verified its correctness with traditional SEA. In 2018, Yuan K. [79]and others applied the EFEA to the randomly excited plate structure. In 2019, Dai W. Q. [80]and others used EFEA to simultaneously study the sound insulation effect of the car body on the high-speed train acoustic cavity and car body structure, and constructed a high-speed train model, then obtained the relevant parameters through simulation calculation and experiments. In 2020, Navazi H. M. [81] and others used EFEA to analyze the high-frequency vibration of the perforated stiffened plate under random vibration. Combined with the high-frequency vibration experiment and the compilation of codes, it was concluded that the EFEA can be used as a method for analyzing high-frequency vibration.
4.5. Uncertainty analysis of interval parameters by using of EFEA
In 2021, Li Z. [82] proposed a corresponding interval analysis method based on the energy flow model of beams and slabs. On this basis, the influence of excitation frequency, wave type, interval parameters, and other factors on the structural response was considered. Since then, the EFEA has begun to develop into the field of interval parameters.
4.6. Simplified EFEA
In the simplified energy finite element analysis, the geometric model is discretized into several governing bodies, and the governing body is taken as the element of research object, and then the finite volume method and the difference method are used to discretize the governing equation, and the energy density and power are obtained at the coupling joint. Finally, a matrix equation similar to the statistical energy method is get, as shown below. Solving this equation, the energy density of each governing body can be obtained:
In 1999, Wang S. and Bernhard R. J. [83] derived a simplified energy finite element equation based on EFEA and the finite volume method (FVM), and proposed the simplified energy finite element analysis (EFEA0). In 2008, Y. G. Wu [84] of Wuhan University of Technology studied the zero-order energy finite element analysis under the guidance of Professor Wu W. G. In 2015, Zhou H. W. et al. [85] proposed an improved zero-order energy finite element analysis based on the governing equations of the plate and acoustic domain energy flow analysis. This improved EFEA can be easily used to model structures with arbitrary shapes. Then improved EFEA was used to solve a simplified car shell and an "L"-shaped coupling plate. The energy density distribution of the corresponding wave field in space is obtained, and the results are compared with SEA and EFEA to verify the correctness of the improved zero-order energy finite element analysis. When using the simplified energy finite element analysis to analyze the vibration response of the coupled structure, there is no need to add nodes at the joint, the model is simpler and the calculation speed is faster, which is beneficial to the application of the EFEA to complex coupled structures.
4.7. The progress of EFEA in software development
(1) In 2007, Hong S. Y. et al. [57] developed an EFEA software for ship structures.
(2) EFEA also attract some commercial software company. For example, in 2012, MSC [86, 87] developed the integrated EFEA analysis module in Nastran software, which can analyze some simple acoustic-vibration couplings by modifying the “*.bdf” file. In 2020, Zhang S. S. [88] of Peking Jiaotong University introduced the characteristics of the EFEA module in Nastran, conducted a noise simulation analysis of a simple cylindrical structure, then she verified the noise simulation. The results show the feasibility of EFEA. Moreover, EFEA can display the sound pressure level profile of the acoustic cavity, which lays a foundation for the subsequent simulation analysis of the EFEA model of the pantograph vehicle. However, this EFEA module in Nastran software can only perform simple structural analysis, such as structures including rib with an annular section, circular section, and rectangular section, it is laboured for more complex structures.
(3) Pera Corporation Ltd has developed the software named Pronas based on the simplified energy finite element analysis. When predicting the vibration response of the coupled structure, the software does not need to set up repeated nodes at the coupling joint, which can solve the high-frequency dynamic response problem of the coupled structure more conveniently and save time, but there is no significant improvement in calculation accuracy.
4.8. Combination of EFEA and topology optimization
In the past 10 years, topology optimization of structural dynamics has also received great attention, and some research work has been carried out successively [89-99]. However, these topology optimization studies are based on the finite element analysis to calculate the dynamic response of the structure, which is very laborious and sometimes even impossible for large-scale plate-shell structures excited by high-frequency.
Owing to high-frequency dynamic topology optimization research is an important means to realize the reliability and safety design of large-scale shell and shell structures, and also an important breakthrough in the integrated design of functional structures in the future, topology optimization research based on EFEA has gradually attracted researcher’s attention in recent years. In 2006, Cho S. et al. [100] deduced the weak form of power flow, using the adjoint sensitivity analysis method, and proposed a density-based topology optimization method (DSA) for the steady-state power flow problem. Design variables is material density, and parameter, such as Young's modulus, density, and damping coefficient, is relative to the material density. The generalized compliance of the structure is taken as the objective function. In 2013, Xue X. G. [91] proposed a topology optimization method for two-material plate structures based on a method similar to Cho S. The goal is to find an optimal material layout to minimize the power flow response for a given load amplitude and frequency. In 2019, Zhao H. T. [101] of Harbin Engineering University proposed a topology optimization method for constrained damped laminates by combining the topology optimization and power flow.
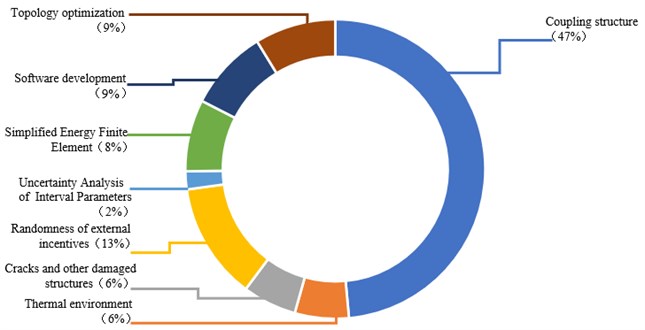
Fig. 3The branch of EFEA theoretical development
In 2021, Liu H. L. et al. [102] established a topology optimization framework based on explicit level sets, in this framework, dynamic response of structure is predicted by EFEA. Finally, the proposed optimization method was used in classical stiffened plates, it has been shown that the proposed EFEA-based topology optimization framework can improve the dynamic performance of high-frequency vibration structural systems by 20 %-80 %.
According to the literature Statistics, the EFEA branch of theoretical development is shown in Fig. 3. It can be seen from the figure that there is large percent in the research for coupled structure (structure-structure coupled structure and acoustic-vibration coupled structure). It may be shown that EFEA is using to more complex structures.
5. Practical applications of EFEA
With the development of the industrial technology, many industrial products tends to be made of light and thin plate or shell, such as automobiles, ships, and aerospace vehicles. The problem of high-frequency vibration and noise is becoming more and more prominent, so the EFEA has gradually gained more and more applications in the fields of aerospace, ships, and automobiles.
5.1. Application of EFEA in Aerospace
From 2008 to 2009, Lima D. et al. [60, 61] began to apply the EFEA to the study of the acoustic-vibration coupling problem of aircraft structures. In 2010, Lee S. M. et al. [103] used the EFEA to analyze the vibration response of a rotorcraft composed of a multi-layer composite laminate structure. In the same year, Xie M. X. et al. [62] analyzed the acoustic-vibration coupling characteristics of the instrument cabin under point source excitation through the developed energy finite element solver. The sound pressure distribution in the instrument cabin and the vibration characteristics of the instrument cabin under the conditions is obtained.
Fig. 4The finite element model of the instrument cabin[64]
![The finite element model of the instrument cabin[64]](https://static-01.extrica.com/articles/22843/22843-img4.jpg)
In 2011, Vlahopoulos et al. [104] proposed an equation for simulating composite laminate structures. In the same year, Xie M. X. et al. [105] combined EFEA with energy boundary element analysis (EBEA) analyzed the sound field inside and outside the instrument cabin of the aircraft; Lin Y. [106] researched the missile cabin structure using EFEA, he derived the energy density governing equation of the finite plate structure and the infinite plate structure. The energy density governing equation of the coupled structure is simulated and analyzed for the two structures. By comparing the simulation results with the exact solution, the correctness of the energy density governing equation of the two structures is verified. Finally, the response prediction of the missile cabin in engineering practice is carried out and the correctness and effectiveness of the prediction are verified, which provides a reference value for the follow-up study of the energy finite element method. In 2019, Wang H. Z. et al. [64] analyzed the energy finite element model (as shown in Fig. 4) of the instrument cabin structure established by the EFEA module in NASTRAN to obtain the energy density distribution of the structure and the sound pressure level distribution of the acoustic cavity. Comparing the results of the sound pressure level of the internal cavity predicted by EFEA with the predicted results of SEA and the experimental test results, the results shown in Fig. 5 show that the energy finite element can better predict the structure in a certain frequency band, which is closer to the measured value than SEA, verifying the upper limit of the frequency that EFEA exists. At the same time, compared with SEA, EFEA can obtain the spatial distribution of the predicted results.
Considering the mechanism characteristics and working environment of aircraft engine blade disc, in 2022, Gao F et al. [107] created the continuous mechanical parameter law of hard coating based on the EFEA considering the strain-dependent complex modulus theory and the composite Mindlin plate theory. An iterative calculation process based on Newton-Raphson method is proposed to solve the nonlinear dynamic characteristics of hard coated monolithic blade disk. Finally, the reliability of the nonlinear dynamic model is verified by numerical and experimental data, and the influence of hard coating and strain dependence on the vibration characteristics of hard coated monolithic blade disk is analyzed.
In the aerospace field, as the structural model becomes more and more complex, compared with finite element and statistical energy models, the use of EFEA modelling to predict the details of the structure is more comprehensive and detailed.
Fig. 5The sound pressure inside the instrument cabin[64]
![The sound pressure inside the instrument cabin[64]](https://static-01.extrica.com/articles/22843/22843-img5.jpg)
5.2. Application of EFEA in ships
In 1999, Vlahopoulos [108] et al. analyzed the application of EFEA in marine engineering structures and verified the feasibility of EFEA in marine engineering structures by comparing the results of EFEA and SEA. In 2003, Sun L. P. and Nie W. [109] analyzed two representative high-frequency dynamic response analysis methods for ship structures: EFEA and SEA. By comparing the advantages and disadvantages of the two methods, it was concluded that EFEA can simulate marine engineering and ship structure vibration. It is a more effective method when EFEA is used, which lays the foundation for the subsequent application of EFEA to ships. From 2004 to 2006, Wu K. C. et al. [110-112] further studied the application of EFEA in ship vibration analysis and carried out corresponding experiments. In 2008, Sun L. P. and Nie W. [3] conducted related research on the simplified structure of a frigate’s base using EFEA. From 2005 to 2010, Zhang W. G. and Raveendra S. T. et al. [51-55] used the EFEA to conduct a series of acoustic-vibration coupling analyses on the ship structure with both acoustic space and structural elements. In 2008, Wu Y. G. [84] researched EFEA0 and studied the application of EFEA0 to ship acoustic-vibration coupling and radiation noise. In 2013, Stritzelberger B. et al. [113] introduced a wave-based EFEA, which uses a finite element mesh to map the energy density of the structures generated by harmonic excitation to the model, because it is based on the low-frequency FEA model, and this method is expected to be integrated into the actual ship design process. Both EFEA and SEA can be coupled in Vinas software, in 2016, Zhang X. W. et al. [114] studied the global noise prediction of a large ship 6700 PCTC based on this kind of vibro-acoustic calculation software and predicted the vibration of all cavity and plate members. Comparing the measured data with the predicted results, they demonstrated the enormous engineering advantages of the EFEA-SEA hybrid technique for ship noise analysis. In September 2021, Jin H. et al. [115] took a large dual-fuel vehicle carrier as an example, used energy finite element and statistical energy hybrid algorithm to predict noise and proposed a noise optimization design scheme under the requirements of MSC.337 (91) and HAB 2016. After that, the effectiveness and accuracy of the prediction results are verified by comparing the noise prediction results with the measured data of the actual ship trial, which has reference significance for the noise optimization design of related similar structures in the future.
The application of the EFEA in ships has become more and more complicated from the gradual complication of the structural model to the structural radiation noise, and then to the field of acoustic-vibration coupling.
5.3. Application of EFEA in the automotive field
In 1999, Vlahopoulos et al. [116] identified a method for modelling spot-welded joints and introduced the development, implementation, and validation of a numerical procedure for evaluating EFEA power transfer coefficients corresponding to spot-welded joints, and applied this method to automobiles. In 2009, Wang A. M. et al. [117] combined EBEA and EFEA methods to predict the noise level inside a vehicle due to external sound sources and provided a complete EBEA/EFEA simulation process for airborne vehicle simulation. From 2005 to 2007, Hong M. N. and others [55-57] used the EFEA to analyze the acoustic and vibration characteristics of vehicles. In 2018, Lin Z. L. [2] studied the energy density of thin plates and their coupled structures. Based on these studies, Lin Z. L. also studied the energy density distribution of automobile body structures. The geometric model of the simplified body was established by commercial 3D design software, as shown in Fig. 6.
Fig. 6Schematic diagram of body structure [2]
![Schematic diagram of body structure [2]](https://static-01.extrica.com/articles/22843/22843-img6.jpg)
Lin Z. L. properly cleaned and simplified the entire car body to obtain the main structure of the car body, imported the geometric model into the finite element pre-processing software for cleaning and repair, obtained the element node values of the car body structure, then used the above element node values to establish the EFEA model. The flexural wave energy density distribution under the engine excitation condition and the unilateral wheel excited torsion condition are discussed. The four bending conditions involved in the unilateral wheel excited torsion condition are: left front wheel, right front wheel left rear wheel and right rear wheel. The vertical direction of the rear wheel and the right rear wheel is raised by 200 mm. In 2020, Zhang S. S. [88] used EFEA to simulate and analyze the noise inside the car. Zhang S. S. verified the superiority of the EFEA by comparing the EFEA and SEA results of a simple cylindrical shell. The conclusion is that the application of EFEA in the automotive field pays more attention to the noise level in the car, external sound field excitation, engine excitation, etc.
With the further research on the thin plate energy finite element equation, coupling junction energy transfer coefficient and composite materials, the energy finite element research on complex vehicle models, body structures and interior noise in the automotive field will gradually be simplified and improved.
6. Conclusions
In short, after more than 30 years of development, EFEA has achieved fruitful research results, and the research on the basic structure has gradually tended to more complex geometric structure forms, more complex material property patterns, and more complex excitation patterns. To apply EFEA to engineering practice, EFEA has also derived several research branches and has gradually been applied in the fields of aerospace, ships, and vehicles. However, there is still a lot of work worth studying to promote the further maturity of EFEA.
1) Although EFEA is based on the traditional discretization method, it needs to use wave theory to establish the relationship between energy density and energy intensity in the structure, which is a very complicated work for structures with changing material parameters and geometric parameters.
2) The current EFEA is based on the linear vibration equation, but in fact, the real structure will inevitably involve nonlinear problems. To use the EFEA to accurately simulate the actual engineering structure, it is necessary to consider geometric nonlinearity and material nonlinearity, and other factors.
3) When the EFEA is applied to a complex coupled structure, the coupling matrix equation can be calculated at the coupling point, and then the required energy transfer coefficient can be solved, and the energy transfer coefficient of different types of coupled structures is also different. This solution is somewhat difficult. To obtain the precise energy density distribution of the coupled structure, the finite element theory of energy at the coupling must be improved or simplified, and the energy transfer coefficient at the connection of the coupled structure must be reasonably characterized so that the energy finite element can be better applied in engineering practice.
4) There are also many problems to be solved in topology optimization based on EFEA, such as how to improve the optimization efficiency under high-frequency excitation of large structures. The setting of different single optimization objective functions and multi-objective functions, optimization problems for different types of structure. And the lack of convenient and practical software that integrates topology optimization and EFEA dynamic response calculation methods.
5) Although the EFEA has outstanding advantages in predicting high-frequency vibration response, however, it is still necessary to consider mid-frequency vibration responses problem that there are both high-frequency vibration components and low-frequency vibration components in the actual composite structure. On the other hand, since the frequency of most vibration problems is below 500 Hz in engineering practice, to effectively predict the vibration response of the structure in the full frequency domain, it is necessary to study how to integrate the EFEA and the finite element method to develop solutions to the full frequency system application software.
References
-
X. H. Miao, X. R. Wang, D. Jia, G. Y. Jin, and F. Z. Pang, “Study on simulation method of high frequency vibration and noise in large complex cylindrical shell,” (in Chinese), Journal of Computational Mechanics, Vol. 29, No. 1, pp. 124–128, 2012.
-
Z. L. Lin, “Research on energy finite element method and its application in vehicle body,” (in Chinese), University of Chinese Academy of Sciences, Ningbo Institute of materials technology and engineering, 2018.
-
L. P. Sun and W. Nie, “Application of energy finite element method in ship structure,” (in Chinese), Journal of Harbin Institute of Technology, No. 9, pp. 1491–1494, 2008.
-
V. D. Belov and S. A. Rybak, Applicability of the Transport Equation in the One-Dimensional Wave-Propagation Problem. 1975.
-
V. D. Belov, S. A. Rybak, and B. D. Tartakovskii, Propagation of Vibrational Energy in Absorbing Structures. 1977.
-
I. A. Butlitskaya, A. I. Vyalyshev, and B. D. Tartakovskii, Propagation of Vibrational and Acoustic Energy Along a Structure with Losses. 1983.
-
D. J. Nefske and S. H. Sung, “Power flow finite element analysis of beam networks,” The Journal of the Acoustical Society of America, Vol. 84, No. S1, pp. S149–S149, Nov. 1988, https://doi.org/10.1121/1.2025857
-
S. C. Burrell, Extension of Power Flow Finite Element Analysis to Ship Structures: Part 1.
-
J. C. Wohlever and R. J. Bernhard, “Mechanical energy flow models of rods and beams,” Journal of Sound and Vibration, Vol. 153, No. 1, pp. 1–19, Feb. 1992, https://doi.org/10.1016/0022-460x(92)90623-6
-
Y. Lase, Description Des Réponses Structurales Dans Le Domaine Des Moyennes Fréquences À L’aide D’une Formulation Énergétique. Ecully, Ecole centrale de Lyon, 1992.
-
Y.-H. Park and S.-Y. Hong, “Vibrational energy flow analysis of corrected flexural waves in timoshenko beam – part II: application to coupled Timoshenko beams,” Shock and Vibration, Vol. 13, No. 3, pp. 167–196, 2006, https://doi.org/10.1155/2006/562762
-
Y. Deng, S. H. Yin, and Z. H. Zhao, “Thermomechanical coupled buckling prediction of functionally graded microplates based on equal geometry finite element method,” (in Chinese), Journal of Computational Mechanics, Vol. 37, No. 5, 2020.
-
J. Yang and Y. Chen, “Free vibration and buckling analyses of functionally graded beams with edge cracks,” Composite Structures, Vol. 83, No. 1, pp. 48–60, 2007, https://doi.org/10.1016/j.compstruct
-
M. Zhang, H. L. Chen, D. H. Zhu, W. B. Zhang, and X. J. Kong, “Random parameter energy finite element analysis of high frequency bending vibration beam,” (in Chinese), Journal of Xi’an Jiaotong University, Vol. 47, No. 11, 2013, https://doi.org/10.7652/xjtuxb201311014
-
H. Deng and W. Cheng, “A damage identification method for functionally graded Timoshenko Beams,” (in Chinese), Journal of Beijing University of Aeronautics and Astronautics, Vol. 42, No. 10, 2016, https://doi.org/10.13700/j.bh.1001-5965.2015.0618
-
Z. Lin, X. Chen, and B. Zhang, “Application of the energy finite element analysis to vibration of beams with stepped thickness and variable cross-section,” Journal of Vibroengineering, Vol. 20, No. 6, pp. 2237–2252, Sep. 2018, https://doi.org/10.21595/jve.2018.19625
-
D. Wang, X. Zhu, T. Y. Li, X. Heng, and S. Gao, “Vibration analysis of functionally graded beams based on energy finite element method,” (in Chinese), Vibration and Impact, Vol. 37, No. 3, 2018.
-
N. Liu, “High frequency vibration analysis method of functionally graded material plate beam coupling structure,” (in Chinese), Harbin Engineering University, 2021.
-
Z. H. Liu, J. C. Niu, and R. H. Jia, “Energy flow model of beam high frequency vibration under thermal gradient environment,” (in Chinese), Journal of Aeronautics, Vol. 43, No. 5, p. 42533, 2021, https://doi.org/10.7527/s1000-6893.2021.25336
-
X. F. Chen, X. Zhu, T. Y. Li, and J. Y. Fu, “Energy finite element analysis of composite laminated beams,” (in Chinese), in 18th Symposium on Underwater Noise of Ships, pp. 510–521, 2021, https://doi.org/10.26914/c.cnkihy.2021.056761
-
M. X. Xie et al., “Energy flow analysis of high-frequency flexural vibration of wedge beam structures,” Shock and Vibration, Vol. 2022, pp. 1–10, Mar. 2022, https://doi.org/10.1155/2022/2935655
-
Y. Lase and L. Jezequel, “Analysis of a dynamic system based on a new energetics formulation,” in Proceedings of the 3rd International Congress on Intensity Techniques, pp. 145–150, 1990.
-
L. P. Sun and W. Nie, “Simplified solution of vibration energy density of rod and beam structures,” (in Chinese), Journal of Harbin Engineering University, Vol. 25, No. 4, 2004.
-
O. M. Bouthier and R. J. Bernhard, “Models of space-averaged energetics of plates,” AIAA Journal, Vol. 30, No. 3, pp. 616–623, Mar. 1992, https://doi.org/10.2514/3.10964
-
O. M. Bouthier and R. J. Bernhard, “Simple models of the energetics of transversely vibrating plates,” Journal of Sound and Vibration, Vol. 182, No. 1, pp. 149–164, Apr. 1995, https://doi.org/10.1006/jsvi.1995.0187
-
X. Yan, Energy Finite Element Analysis Developments for High Frequency Vibration Analysis of Composite Structures. 2008.
-
S.-J. Moraveji, Modeling of Trim Panels in the Energy Finite Element Analysis. 2008.
-
W. H. Zhu, X. R. Ma, Z. Y. Han, and Y. J. Zou, “Energy flow analysis of plate structures based on finite element method,” (in Chinese), Strength and Environment, No. 2, 2014, https://doi.org/10.3969/j.issn.1006-3919.2014.02.001
-
L. He, T. N. Chen, and C. Chen, “Vibration energy transfer characteristics of orthotropic thin plates,” (in Chinese), Journal of Xi’an Jiaotong University, Vol. 53, No. 3, 2019, https://doi.org/10.7652/xjtuxb201903008
-
Z. Cai, R. Zhong, T. Liu, and Q. Wang, “Inplane vibration research of rectangular laminated plates under general boundary conditions,” Journal of Harbin Engineering University, Vol. 43, No. 6, pp. 865–872, 2022.
-
O. M. Bouthier and R. J. Bernhard, “Space‐averaged energetics of membranes and plates,” The Journal of the Acoustical Society of America, Vol. 87, No. S1, pp. S92–S92, May 1990, https://doi.org/10.1121/1.2028427
-
O. M. Bouthier and R. J. Bernhard, “Simple models of energy flow in vibrating membranes,” Journal of Sound and Vibration, Vol. 182, No. 1, pp. 129–147, Apr. 1995, https://doi.org/10.1006/jsvi.1995.0186
-
K. Wang, Q. Zhang, and J. Liu, “Vibration prediction of space large-scale membranes using energy flow analysis,” Applied Sciences, Vol. 12, No. 12, p. 6238, Jun. 2022, https://doi.org/10.3390/app12126238
-
M. X. Xie, H. L. Chen, and J. H. Wu, “Energy finite element analysis of high frequency bending vibration of cylindrical shells,” (in Chinese), Journal of Xi’an Jiaotong University, Vol. 42, No. 9, 2008, https://doi.org/10.3321/j.issn:0253-987x.2008.09.011
-
H. Dong, “A new method for solving high frequency vibration problems,” (in Chinese), Master Thesis, Xi’an Jiaotong University, Xi'an, 2008.
-
X. Kong, H. Chen, D. Zhu, and W. Zhang, “Study on the validity region of energy finite element analysis,” Journal of Sound and Vibration, Vol. 333, No. 9, pp. 2601–2616, Apr. 2014, https://doi.org/10.1016/j.jsv.2013.11.047
-
A. Nikiforov, “Estimating the intensity of structure-borne noise in ribbed structures,” in International Congress on Intensity Techniques, pp. 115–119, 1990.
-
N. A. S., Structural Acoustics of Ships. Russian: Russian Academic of Science, 1974, pp. 35–45.
-
L. E. Buvailo and A. V. Ionov, “Application of the finite element method to the investigation of the vibroacoustical characteristic of the structures at high frequencies,” Soviet Physics Acoustics, Vol. 26, No. 4, pp. 149–166, 1980.
-
P. E. Cho and R. J. Bernhard, “Energy flow analysis of coupled beams,” Journal of Sound and Vibration, Vol. 211, No. 4, pp. 593–605, Apr. 1998, https://doi.org/10.1006/jsvi.1997.1350
-
J. Niu and K. Li, “Energy finite element analysis of N-shaped plate structures with three types of wave,” in 9Th International Conference on Vibration Engineering and Technology of Machinery (VETOMAC-IX), 2013.
-
M. S. Jiang, “Finite element analysis of power flow for energy transfer of arbitrary plates and coupled structures,” (in Chinese), Shandong University, 2015.
-
Z. H. Liu, J. C. Niu, Y. Q. Zhou, and G. Yue, “Analysis of multi plate coupled structure based on energy finite element method,” in 27th National Conference on Vibration and Noise Applications, 2016.
-
Z. H. Liu, “Research on dynamic characteristics of closed coupled structures based on energy finite element method,” (in Chinese), Shandong University, 2017.
-
J. Zeng, H. B. Chen, and Y. Y. Wang, “Fatigue life estimation algorithm of structures with high frequency random vibration based on hybrid energy finite element method,” Vibroengineering Procedia, Vol. 11, pp. 29–33, May 2017, https://doi.org/10.21595/vp.2017.18568
-
Y. Ge, “On energy transmission characteristics of coupled plates with arbitrary coupling angles to multiple types of excitation,” (in Chinese), Journal of Mechanical Engineering, Vol. 53, No. 7, p. 94, 2017, https://doi.org/10.3901/jme.2017.07.094
-
P. Xu, T. Liu, S. Pan, and Z. Zhou, “Numerical analysis for micro-vibration isolation of jointed sandwich plates with mass blocks,” Materials Today Communications, Vol. 17, pp. 341–354, Dec. 2018, https://doi.org/10.1016/j.mtcomm.2018.09.018
-
Z. H. Liu, J. C. Niu, and X. Gao, “An improved approach for analysis of coupled structures in energy finite element analysis using the coupling loss factor,” Computers and Structures, Vol. 210, pp. 69–86, Nov. 2018, https://doi.org/10.1016/j.compstruc.2018.08.017
-
L. He, T. N. Chen, and C. Chen, “Solving the energy density of hollow thin plates,” (in Chinese), Noise and Vibration Control, Vol. 38, 2018, https://doi.org/10.3969/j.issn.1
-
F. Bitsie and R. J. Bernhard, “Structural acoustic energy finite element method.,” (in Chinese), The Journal of the Acoustical Society of America, Vol. 99, No. 4, pp. 2585–2603, Apr. 1996, https://doi.org/10.1121/1.415117
-
W. Zhang and S. T. Raveendra, “Interior noise prediction based on energy finite element method,” in SAE 2005 Noise and Vibration Conference and Exhibition, May 2005, https://doi.org/10.4271/2005-01-2332
-
S. T. Raveendra and W. Zhang, “Vibro-acoustic analysis using a hybrid energy finite element /boundary element method,” SAE 2007 Noise and Vibration Conference and Exhibition, Vol. 1, May 2007, https://doi.org/10.4271/2007-01-2177
-
W. Zhang and S. T. Raveendra, “Application of energy finite element method for high frequency vibroacoustic analysis,” in National Conference on Noise Control Engineering, 2008.
-
W. Zhang and S. T. Raveendra, “High frequency vibro-acoustic analysis using energy finite element method,” SAE International Journal of Passenger Cars – Mechanical Systems, Vol. 2, No. 1, pp. 822–831, Apr. 2009, https://doi.org/10.4271/2009-01-0771
-
N. Vlahopoulos and K. Wu, “Energy finite element analysis of naval vehicles,” The Journal of the Acoustical Society of America, Vol. 127, No. 3, p. 1850, 2010, https://doi.org/10.1002/97811186939
-
R. Fischer, L. Boroditsky, L. Gilfroy, and D. Brennan, “Energy finite energy analysis for shipboard noise,” The Journal of the Acoustical Society of America, Vol. 120, No. 5, pp. 3287–3287, Nov. 2006, https://doi.org/10.1121/1.4777627
-
S.-Y. Hong, H.-W. Kwon, and J.-D. Kim, “Car interior and exterior multi-domain noise analysis using energy flow analysis (EFA) software, NASEFAC++,” in SAE 2007 Noise and Vibration Conference and Exhibition, May 2007, https://doi.org/10.4271/2007-01-2174
-
P. A. Manning, “Energy finite element analysis of a vehicle floor,” SAE 2005 Noise and Vibration Conference and Exhibition, Vol. 79, May 2005, https://doi.org/10.4271/2005-01-2420
-
S.B. Homg and N. Vlahopoulos, “Application of a hybrid finite‐element formulation for structure‐borne vibration in an automotive vehicle structure,” The Journal of the Acoustical Society of America, Vol. 119, No. 5, pp. 3297–3298, May 2006, https://doi.org/10.1121/1.4786242
-
W. J. de Lima, N. Vlahopoulos, R. Sbragio, and J. He, “Interior aircraft noise computations due to TBL excitation using the energy finite element analysis,” in SAE 2009 Noise and Vibration Conference and Exhibition, May 2009, https://doi.org/10.4271/2009-01-2248
-
W. J. D. Lima, A. Wang, and N. Vlahopoulos, “Application of energy finite elements in the prediction of the vibroacoustic ground response of business jet,” in INTER-NOISE and NOISE-CON Congress and Conference Proceedings, 2008.
-
M. X. Xie, H. L. Chen, J. H. Wu, and F. G. Sun, “Application of energy finite element method to high-frequency structural-acoustic coupling of an aircraft cabin with truncated conical shape,” CMES-Computer Modeling in Engineering and Sciences, Vol. 61, pp. 1–22, 2010, https://doi.org/10.3970/cmes.2010.061.001
-
S. Wang, “Noise prediction of a sedan vehicle using EFEA-SEA hybrid technique,” in INTER-NOISE and NOISE-CON Congress and Conference Proceedings, 2017.
-
H. Z. Wang, K. P. Yu, Z. Q. Zhang, Y. X. Zeng, and X. Wang, “Prediction of medium frequency acoustic vibration environment of energy finite element of instrument cabin structure,” (in Chinese), Vibration and Shock, Vol. 38, No. 10, 2019.
-
A. Li, “Research on energy transfer characteristics of coupled structures,” (in Chinese), Master Thesis, University of Science and Technology of China, 2021.
-
L. J. Zhu, H. S. L. H. Wen, and Y. H. Liu, “Analytical model of floating foundation vibration reduction system based on energy method,” (in Chinese), Earthquake Engineering and Engineering Vibration, Vol. 42, No. 2, pp. 104–112, 2022, https://doi.org/10.13197/j.eeed.2022.0211
-
J. Liu, L. Zeng, X. Guo, P. Wang, and L. Dai, “Multi-field coupling nonlinear vibration characteristics of hydraulic lifting pipe in deep-ocean mining,” Applied Ocean Research, Vol. 120, p. 103074, Mar. 2022, https://doi.org/10.1016/j.apor.2022.103074
-
A. Li, H. B. Chen, Q. Zhong, and X. Wang, “Energy transfer characteristics of orthotropic laminated plate and shell coupling structures,” (in Chinese), Vibration and Shock, Vol. 41, No. 5, pp. 9–19, 2022, https://doi.org/10.13465/j.cnki.jvs.2022.05.002
-
W. Zhang, H. Chen, D. Zhu, and X. Kong, “The thermal effects on high-frequency vibration of beams using energy flow analysis,” Journal of Sound and Vibration, Vol. 333, No. 9, pp. 2588–2600, Apr. 2014, https://doi.org/10.1016/j.jsv.2013.12.020
-
D. Wang, M. X. Xie, and Y. M. Li, “High-frequency dynamic analysis of plates in thermal environments based on energy finite element method,” Shock and Vibration, Vol. 2015, pp. 1–14, 2015, https://doi.org/10.1155/2015/157208
-
Z. Chen, Z. Yang, N. Guo, and G. Zhang, “An energy finite element method for high frequency vibration analysis of beams with axial force,” Applied Mathematical Modelling, Vol. 61, pp. 521–539, Sep. 2018, https://doi.org/10.1016/j.apm.2018.04.016
-
F. H. Xu, “Research on energy finite element method for prediction of high frequency response in structures,” (in Chinese), Nanjing University of Aeronautics and Astronautics, 2012.
-
D. Wang, X. Zhu, T. Y. Li, S. Gao, and X. Heng, “Vibration analysis of damaged plate structure based on energy finite element method,” (in Chinese), Vibration and Impact, Vol. 36, No. 11, 2017, https://doi.org/10.13465/j.cnki.jvs.2017.11.011
-
B. Y. Shang, X. Zhu, T. Y. Li, and X. T. Liang, “Vibration analysis of damaged liquid filled pipeline based on energy finite element method,” Vibration and Shock, Vol. 38, No. 21, 2019.
-
J. You, G. Meng, H. G. Li, and M. Wang, “Finite element analysis of frame beam structure energy under random excitation,” (in Chinese), Journal of Shanghai Jiaotong University, No. 10, 2009.
-
J. You, H. G. Li, and G. Meng, “Random energy finite element analysis of coupled plate structures,” (in Chinese), Vibration and Impact, Vol. 28, pp. 43–46, 2009.
-
J. You, G. Meng, and H. G. Li, “Analysis of high frequency random energy flow under correlated excitation of L-type coupling plate,” (in Chinese), Journal of Vibration Engineering, Vol. 23, No. 1, 2010, https://doi.org/10.3969/j.issn.1004-4523.2010.01.011
-
J. Yu, “Analysis and research of structural random energy flow,” (in Chinese), Shanghai Jiaotong University, 2010.
-
K. Yuan, J. M. Wang, C. H. Qin, L. Han, and Z. Zhong, “Research on input power of energy finite element based on admittance correction,” (in Chinese), Intensity and Environment, Vol. 45, pp. 8–15, 2018.
-
W. Q. Dai, X. Zheng, Z. Y. Hao, and Y. Qiu, “Prediction of interior noise of high-speed trains using energy finite element analysis,” (in Chinese), Journal of Zhejiang University: Engineering Edition, Vol. 53, No. 12, 2019, https://doi.org/10.3785/j.issn.1008-973x.2019.1
-
A. Nokhbatolfoghahai, H. Navazi, and H. Haddadpour, “High-frequency random vibrations of a stiffened plate with a cutout using energy finite element and experimental methods,” Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, Vol. 234, No. 16, pp. 3297–3317, Aug. 2020, https://doi.org/10.1177/0954406220914328
-
Z. Li, “Uncertainty analysis of energy finite element model of beam slab structure,” (in Chinese), Shandong University.
-
S. Wang and R. J. Bernhard, “A zero-order energy finite element method: Theory, applications, and similarity to SEA,” in INTER-NOISE and NOISE-CON Congress and Conference Proceedings, 1999.
-
Y. G. Wu, “Zero order energy finite element method and its application in sound radiation of ship structures,” (in Chinese), Wuhan University of Technology, 2008.
-
H. W. Zhou, H. B. Chen, and Y. Y. Wang, “Non structural zero order energy finite element analysis of coupled plate structures,” Vibration and Shock, Vol. 34, No. 13, pp. 140–145, 2015, https://doi.org/10.13465/j.cnki.jvs.2015.13.024
-
T. A. S. Foundation, Apache Axis2 User’s Guide. 2012.
-
E. Dumbill, What is Apache Hadoop?. 2012.
-
S. S. Zhang, “Research on Simulation and analysis method of vehicle interior noise based on energy finite element,” (in Chinese), Master Thesis, Beijing Jiaotong University, 2020.
-
Q. Zhang, W. H. Zhang, and J. H. Zhu, “Structural topology optimization design under dynamic response constraints,” (in Chinese), Journal of Mechanical Engineering, Vol. 15, 2010, https://doi.org/10.3901/jme.200.15.045
-
H. Liu, “Research on key problems of topology optimization in structural dynamics,” (in Chinese), Northwestern Polytechnical University, 2015.
-
X. G. Xue, “Research on topology optimization theory and method of structural dynamics based on energy flow analysis,” (in Chinese), National University of Defense Science and Technology, 2013.
-
L. Y. Chen and Y. F. Zhang, “Research on structural dynamic optimization based on improved progressive structural optimization method,” (in Chinese), Journal of Vibration Engineering, Vol. 27, No. 1, 2014, https://doi.org/10.3969/j.issn.1004-4523.2014.01.007
-
W. Zhang, D. Li, J. Zhou, Z. Du, B. Li, and X. Guo, “A Moving Morphable Void (MMV)-based explicit approach for topology optimization considering stress constraints,” Computer Methods in Applied Mechanics and Engineering, Vol. 334, pp. 381–413, Jun. 2018, https://doi.org/10.1016/j.cma.2018.01.050
-
X. R. Peng and Y. K. Sui, “ICM method for topology optimization of continuum structures considering damage safety,” (in Chinese), Journal of Mechanics, Vol. 50, No. 3, p. 11, 2018, https://doi.org/10.6052/0459-1879-17-366
-
H. L. Ye, Y. M. Li, Y. M. Zhang, and Y. K. Sui, “Research on topological optimization method of plate and shell structure dynamics,” (in Chinese), in Proceedings of China Computational Mechanics Conference 2014 and the 3rd Gianlingxi Computational Mechanics Award Ceremony, 2014.
-
N. Olhoff and J. Du, “Erratum to: Generalized incremental frequency method for topological design of continuum structures for minimum dynamic compliance subject to forced vibration at a prescribed low or high value of the excitation frequency,” Structural and Multidisciplinary Optimization, Vol. 54, No. 5, pp. 1143–1143, Nov. 2016, https://doi.org/10.1007/s00158-016-1608-x
-
H. J. Zhong, “Research on topology optimization method of thin-walled stiffened structures,” (in Chinese), Nanjing University of Aeronautics and Astronautics, 2015.
-
M. Xu, S. Wang, and X. Xie, “Level set-based isogeometric topology optimization for maximizing fundamental eigenfrequency,” Frontiers of Mechanical Engineering, Vol. 14, No. 2, pp. 222–234, Jun. 2019, https://doi.org/10.1007/s11465-019-0534-1
-
H. Liu, B. Li, Z. Yang, and J. Hong, “Topology optimization of stiffened plate/shell structures based on adaptive morphogenesis algorithm,” Journal of Manufacturing Systems, Vol. 43, pp. 375–384, Apr. 2017, https://doi.org/10.1016/j.jmsy.2017.02.002
-
S. Cho, C.-Y. Park, Y.-H. Park, and S.-Y. Hong, “Topology design optimization of structures at high frequencies using power flow analysis,” Journal of Sound and Vibration, Vol. 298, No. 1-2, pp. 206–220, Nov. 2006, https://doi.org/10.1016/j.jsv.2006.05.015
-
H. T. Zhao, Topology Optimization Method of Constrained Damping Laminated Plates Based on Energy Flow Analysis. (in Chinese).
-
H. L. Liu, Z. Y. Zhang, B. T. Li, M. X. Xie, H. Jun, and S. Zheng, “Topology optimization of high frequency vibration problems using the EFEM-based approach,” Thin-Walled Structures, Vol. 160, p. 107324, Mar. 2021, https://doi.org/10.1016/j.tws.2020.107324
-
S.-M. Lee, “Energy finite element method for high frequency vibration analysis of composite rotorcraft structures,” Ph.D. Thesis, University of Michigan, 2010.
-
N. Vlahopoulos, N. Schiller, and S. Lee, “Energy finite element analysis developments for vibration analysis of composite aircraft structures,” SAE International Journal of Aerospace, Vol. 4, No. 2, pp. 593–601, May 2011, https://doi.org/10.4271/2011-01-1734
-
M. X. Xie, H. L. Chen, and J. H. Wu, “Transient energy density distribution of a rod under high-frequency excitation,” Journal of Sound and Vibration, Vol. 330, No. 12, pp. 2701–2706, Jun. 2011, https://doi.org/10.1016/j.jsv.2011.02.028
-
Y. Lin, “Research on load environment prediction of missile cabin structure based on energy finite element method,” (in Chinese), Harbin Institute of Technology, 2012.
-
F. Gao, X. T. Liu, and G. X. Hua, “Study on nonlinear vibration characteristics of Blisk coated with strain dependent hard coating,” (in Chinese), Vibration and Shock, Vol. 41, No. 3, pp. 199–208, 2022, https://doi.org/10.13465/j.cnki.jvs.2022.03.024
-
N. Vlahopoulos, L. O. Garza-Rios, and C. Mollo, “Numerical Implementation, validation, and marine applications of an energy finite element formulation,” Journal of Ship Research, Vol. 43, No. 3, pp. 143–156, Sep. 1999, https://doi.org/10.5957/jsr.1999.43.3.143
-
L. P. Sun and W. Nie, “Development of methods in analyzing ship structure vibration noise,” Journal of Ship Mechanics, 2003.
-
K. Wu and N. Vlahopoulos, “Vibratory response of surface ships predicted by energy finite element approach,” The Journal of the Acoustical Society of America, Vol. 116, No. 4, pp. 2569–2569, Oct. 2004, https://doi.org/10.1121/1.4785257
-
K. Wu and N. Vlahopoulos, “Numerical investigation of small‐scale surface ships by energy finite‐element analysis,” The Journal of the Acoustical Society of America, Vol. 119, No. 5, pp. 3297–3297, May 2006, https://doi.org/10.1121/1.4786241
-
K. Wu and N. Vlahopoulos, “Recent developments and applications of energy finite‐ element analysis,” The Journal of the Acoustical Society of America, Vol. 120, No. 5, pp. 3343–3343, Nov. 2006, https://doi.org/10.1121/1.4781359
-
B. Stritzelberger, M. Abele, and O. Von Estorff, “On the energy finite element method for the acoustic design of ships,” The Journal of the Acoustical Society of America, Vol. 133, No. 5, pp. 3599–3599, May 2013, https://doi.org/10.1121/1.4806664
-
Xinwei Zhang, Shawn Wang, and Jinxiang Pang, “Noise prediction of large ship 6700 PCTC using EFEA-SEA hybrid technique,” in INTER-NOISE and NOISE-CON Congress and Conference Proceedings, p. 6700, 2016.
-
H. Jin, X. W. Zhang, M. T. Liu, and Y. C. Ma, “Noise prediction and optimization design of large-scale dual fuel vehicle carrier,” (in Chinese), Ship Design Communication, pp. 58–64, 2021.
-
N. Vlahopoulos, X. Zhao, and T. Allen, “An approach for evaluating power transfer coefficients for spot-welded joints in an energy finite element formulation,” Journal of Sound and Vibration, Vol. 220, No. 1, pp. 135–154, Feb. 1999, https://doi.org/10.1006/jsvi.1998.1942
-
A. Wang and N. Vlahopoulos, “Vehicle NVH analysis using EFEA and amp; EBEA methods,” SAE International Journal of Passenger Cars – Mechanical Systems, Vol. 2, No. 1, pp. 814–821, Apr. 2009, https://doi.org/10.4271/2009-01-0766
Cited by
About this article
This work was supported by the Natural Science Foundation of Shaanxi Province, China Grant (No. 2020JM-484) and National Natural Science Foundation of China, Grant (No. 51305330).
The datasets generated during and/or analyzed during the current study are available from the corresponding author on reasonable request.
The authors declare that they have no conflict of interest.
