Relating structural damage to modal frequencies shift using low cost LQG-FEA approach and minimal feedback measurements

2.1. State-space representation of the pipe system

Considering the nodal coordinates of the pipe’s structure, its dynamics can be described by the second order matrix differential equations:

where q is the $n\times 1$ nodal displacements vector, $\mathbf{w}$ is the $m\times 1$ external input vector, ${\mathbf{Y}}_s$ is the $p\times 1$ nodal output vector, $\mathbf{M}$ (mass matrix) is $n\times n$ positive definite, $\mathbf{G}$ (damping matrix) $n\times n$ positive semidefinite, $\mathbf{K}$ (stiffness matrix) $n\times n$ positive semidefinite, ${\mathbf{C}}_d$ and ${\mathbf{C}}_v$ are the $p\times n$ output displacement and output velocity matrices, respectively.

Eqs. (1) and (2) are $n$ dimensional, where $n$ is the number of nodes in the finite element model. Knowing that $n$ is large for large structures, the numerical burden makes difficult to produce a working state-space model suitable for structural estimation and control applications. Thus, $N$ dimensional second-order modal model can be used instead, where $N\ll n$ [22-24]:

where $\mathbf{\eta }=\mathbf{\Phi }\mathbf{q}$, $\mathbf{\Phi }$ is the $n\times N$ modal matrix, $\mathbf{\Omega }$ is the $N\times N$ diagonal matrix of Modal frequencies, $\mathbf{Z}$ is the $N\times N$ modal damping matrix, ${\mathbf{B}}_m$ is the $N\times p$ modal input matrix, ${\mathbf{C}}_{md}$ is $l\times N$ modal displacement matrix, and ${\mathbf{C}}_{mv}$ is $l\times N$ modal velocity matrix, where $p$ and $l$ are the number of inputs and outputs, respectively. Thus, the linear, time-invariant (LTI) modal model takes on the form:

Defining a new state vector $\mathbf{z}={\left[{\mathbf{z}}_1{\mathbf{}\mathbf{}\mathbf{z}}_2\right]}^T={\left[\mathbf{\eta }\mathbf{}\mathbf{}\dot{\mathbf{\eta }}\right]}^T$, the state-space representation of the structure having point forces as the inputs and point accelerations as the outputs is expressed as:

where: ${\mathbf{C}}_{ma}={\mathbf{C}}_a\mathbf{\Phi }\text{,}$${\mathbf{C}}_N=\left[\begin{array}{cc}-{\mathbf{C}}_{ma}{\mathbf{\Omega }}^2& -2{\mathbf{C}}_{ma}\mathbf{Z}\mathbf{\Omega }\end{array}\right]=-{\mathbf{C}}_{ma}\left[\begin{array}{cc}{\mathbf{\Omega }}^2& 2\mathbf{Z}\mathbf{\Omega }\end{array}\right]$ and ${\mathbf{G}}_N={\mathbf{C}}_{ma}{\mathbf{B}}_m\text{,}$ where ${\mathbf{C}}_a$ is the accelerometer locations matrix. Assuming proportional damping then ${\mathbf{M}}^{-1}\mathbf{G}=2\mathbf{Z}\mathbf{\Omega }$ such that $\mathbf{Z}$ and $\mathbf{\Omega }$ are as defined above. The model constructed in Eqs. (1-8) is the full order modal model of the structure. This is usually a large model if the structure is large with significant number of modes are required to construct a viable model. Thus, the calculations cost associated with implementing such model for vibration estimation and vibration analysis is still high although it is much smaller than the nodal model of Eqs. (1) and (2). Therefore, model reduction is an option provided that accuracy is maintained while reducing mathematical burden. The time-domain linear time-invariant reduced order state-space model of the structure is expressed as:

where ${\mathbf{A}}_r\in R^r$ such that $r\ll N$.

3.1. LQG structure and closed loop model

For both full and reduced order continuous-time LTI models given above, assuming a zero-order hold (ZOH) and sampling and command updates at time intervals $T$ such that $kT\le t\le (k+1)T$, $k=\mathrm{0,1},\dots \infty$, where $t$ is the time, then the linear discrete-time state-space model of the system is expressed as:

where for the full order system, ${\mathbf{A}=\mathbf{e}}^{{\mathbf{A}}_N\mathbf{T}}$ and $\mathbf{B}={\mathbf{e}}^{{\mathbf{A}}_N\mathbf{T}}{\int }_0^{\mathbf{T}}{\mathbf{e}}^{{\mathbf{A}}_N\mathbf{\tau }}d\tau$ while for the reduced order model, ${\mathbf{A}=\mathbf{e}}^{{\mathbf{A}}_r\mathbf{T}}$and $\mathbf{B}={\mathbf{e}}^{{\mathbf{A}}_r\mathbf{T}}{\int }_0^{\mathbf{T}}{\mathbf{e}}^{{\mathbf{A}}_r\mathbf{\tau }}d\tau$. ${\mathbf{w}}_k$ and ${\mathbf{v}}_k$, are zero mean uncorrelated Process and measurement noise, respectively.

Following the procedure presented in [26], estimated states using Kalman Filter is generated in two steps namely, predictive and update, such that in the predictive step, and before the output ${\mathbf{y}}_k$ is obtained, (i.e. priori estimate), the state estimates and the associated error covariance are expressed, respectively in the form:

After measurement of the output ${\mathbf{y}}_k$ are obtained, the update equations takes on the form:

The difference $\left({\mathbf{y}}_k-\mathbf{C}{\widehat{\mathbf{x}}}_{k+1|k}-\mathbf{D}u\right)$ in Eqs. (14) is called the innovation and ${\mathbf{L}}_k$ is the observer gain. The error between the true state and the estimated values of the states is denoted as ${\mathbf{\epsilon }}_{\mathbf{k}}$ such that the state prediction error covariance is ${\mathbf{P}}_k=\mathbf{E}\left\{\left({\mathbf{x}}_k-{\widehat{\mathbf{x}}}_k\right){\left({\mathbf{x}}_k-{\widehat{\mathbf{x}}}_k\right)}^T\right\}$. The gain ${\mathbf{L}}_k$ is determined by proper selection of elements of ${\mathbf{Q}}_w$ and ${\mathbf{R}}_v$ such that:

${\mathbf{Q}}_w$ and ${\mathbf{R}}_v$ are symmetric matrices whose values are selected depending on the transient response and measurement qualities [27-30].

Assuming that the structure is time-invariant in the sense that the states converge to zero much faster than the parameters can change, the objective of the LQR is to drive the states to zero in an optimal manner. Moreover, we demand that the error goes to zero for best estimates. Since the LQR requires full state feedback and with the availability of the state estimates from the LQE given in the previous section, the associated Riccati equation solution provides the optimal state feedback gain that minimizes the quadratic cost function:

where ${\mathbf{Q}}_{LQR}$ is positive semi-definite matrix and ${\mathbf{R}}_{LQR}$ is positive definite matrix. The state feedback regulator is of type:

It is clear that the feedback given in Eq. (18) will bring the states of the system given in Eq. (11) to zero in an optimal fashion. Since the states of the system have different non-zero initial states, entries of ${\mathbf{Q}}_{LQR}$ are chosen such that various states are driven to zero at various speeds. Entries of ${\mathbf{R}}_{LQR}$ are determined so as to prevent excessively large control moves. If the proposed controller runs for a sufficiently long time, it will yield a stationary Kalman Filter and Regulator for which the values of LQE and LQR gains can be expressed simply by limiting gain values of $L$ and $K$, respectively.

3.2. Closed-loop system eigen values and stability

Combining the LQE and LQR is known as the linear quadratic Gaussian (LQG) controller. Examining the stability of the LQE-LQR system, where the combined error and state estimation unforced dynamics of the closed-loop system are expressed by:

Defining a new matrix $\mathbf{\Psi }$ such that, $\mathbf{\Psi }=\left[\begin{array}{ll}\mathbf{A}-\mathbf{B}\mathbf{K}& -\mathbf{B}\mathbf{K}\\ \left[0\right]& \mathbf{A}-\mathbf{L}\mathbf{C}\end{array}\right]$ where matrix $\mathbf{\Psi }$ is an upper triangular matrix for which the Eigen Values are:

Notice here that the observer gain $\mathbf{L}$ can be designed independently from the regulator gain $\mathbf{K}$ by the separation principle [31-33]. In Eq. (20), ${\lambda }_i$ is the $i$thEigen Value of the corresponding matrix.

If we refer to the closed-loop model of the system dynamics presented in Eq. (19) as the healthy structure, then the Eigen values and Eigen vectors of $\mathbf{\Psi }$ represent the predicted or estimated Modal frequencies and mode shapes of the structure. We notice that those frequencies are best estimates of those of the structure. This leads to the next concept in this research which is the prediction of any damage or structural parameter changes that might occur after a certain period of time while the structure is in operation. Keeping the LQG servo control gains the same at all times, any change in the structural parameters will alter the actual values of $\mathbf{A}$, $\mathbf{B}$, $\mathbf{C}$ and $\mathbf{D}$. In that case, a damaged or altered system will have a state-space model of the form similar to the one in Eq. (11) but will be expressed as:

$\stackrel{-}{\mathbf{A}}$, $\stackrel{-}{\mathbf{B}}$,$\stackrel{-}{\mathbf{C}}$ and $\stackrel{-}{\mathbf{D}}$ are the previously defined matrices of the damaged system. Therefore, the Eigen values of the closed-loop model of the damaged systems will be:

Notice that the damage to the structure will appear in the in closed-loop model estimated response as shifts in some or all of its Eigen values. The shift is expressed as:

Non zero values of $\mathbf{\delta }$ gives a strong indication that the structure has been altered or damaged.

Defining the unforced dynamics of the full-order closed-loop system (CLFOM) and the reduced-order closed-loop systems as ${\mathbf{\Psi }}_F$ and ${\mathbf{\Psi }}_R$, respectively, and the stability margin as:

Then the CLROM is stable if $\underset{\_}{\mathbf{M}}\left({\mathbf{\Psi }}_R\right)\cong \mathbf{M}\left({\mathbf{\Psi }}_F\right)$ which is the case if the model is open-loop stable and the controller is designed such that all ${\lambda }_j$’s are within a unit circle; see page 272 of [23]. The following section shows numerically and experimentally that damage inflicted on the structure can be detected from shifts in the natural frequencies predicted by the response of the closed-loop model.

4.1. Finite element model

The structure used in this study is an AISI 1020 Low Carbon Steel pipe section shown in Figs. 1 and 2, and has the properties listed in Table 1. The FEA model of the pipe is generated and meshed using ANSYS software package. The latter has 7202 SOLID187, SOLID185 elements and 10966 nodes. Table 2 lists the values of Modal frequencies calculated by ANSYS as-well-as the actual ones obtained from experimental impulse force test of the pipe section. It is clear from Table 2 that FEA Modal frequencies are different from the experimental ones. This is so, for two reasons namely, (a) the FEA model is only a representation of the actual structure and (b) some modes predicted by FEA have negligible contribution to the response in the direction of measurement and/or at the location of sensor placement. Thus, the two aforementioned reasons motivated the use of LQG servo-control and modal reduction to minimize model-plant mismatch.

Acceleration measurement is carried out using three PCB uniaxial accelerometers attached to the pipe’s outer surface and have the specs listed in Table 3. All accelerometers measure the acceleration in the $y$-direction which is perpendicular to the ground. Measurement obtained from the Right accelerometer is the only feedback signal to the LQG servo controller. Measurements of Middle and Left accelerometers are only used for evaluating the accuracy of model estimates at the corresponding locations. The targeted outcomes of this work are: 1) Utilize minimal number of physical measurements (Right acceleration) to generate accurate estimates of acceleration at any location on the pipe without the need to place an accelerometer at that location, and 2) Use estimates, instead of actual measurements, to predict variations in structural parameters (i.e. structural failure).

Fig. 1Solid model of the pipe section

4.2. Implementation of servo controlled model in $\mathit{Y}$-direction

The implementation of the proposed approach is presented in the schematic of the servo controlled closed-loop system shown in Fig. 3. In the following, the input force is applied to the pipe by the instrumented hummer shown in Fig. 2, in the vicinity of the Right accelerometer. Numerical evaluation of the proposed estimation technique is carried out by exciting the structure with multiple hammer hits near the Right accelerometer and collecting the acceleration data at positions a, b and c as indicated in Table 3. A sample input-output data is shown in Fig. 4.

Fig. 2Experimental setup and data acquisition hardware

Data is collected with a dSPACE CP 1104 unit, which also has the closed-loop model built into it. LQR gain vector is determined by proper setting of the elements of ${\mathbf{Q}}_{LQR}\in R^N$ for the full-order model and ${\mathbf{Q}}_{LQR}\in R^r$ for reduced-order model. The value chosen for ${\mathbf{R}}_{LQR}\in R^1$ since we have one external input to the system. Small value of ${\mathbf{R}}_{LQR}$ is chosen to prevent excessive control input to the model. On the other hand, large elements of ${\mathbf{Q}}_{LQR}$ matrix are designed to bring all the states to the unperturbed state values, faster. Data is collected at a sampling frequency of 10 kHz, which is high compared to the highest considered Eigen frequency of the pipe, but was necessary for the stability of the Matlab Solver handling the numerical calculations. The LQE gain matrix is determined such that the error between estimates and actual is minimized. Entries of ${\mathbf{Q}}_w$ are selected to achieve minimal estimation error. Matrix ${\mathbf{R}}_v\in R^3$ is set to identity since measurement noise is similar for fully functional and identical accelerometers.

Fig. 3Schematic of the servo controlled system used for acceleration estimation

Fig. 4Input-output data from pipe

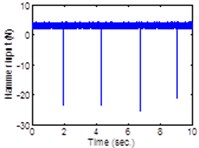
a) Hammer force input

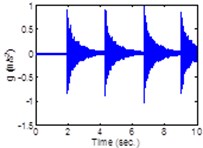
b) Right accel

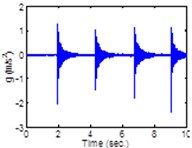
c) Middle accel

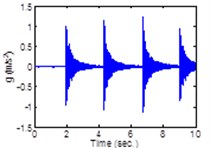
d) Left accel

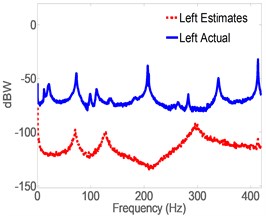
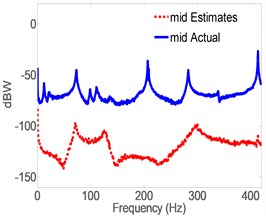
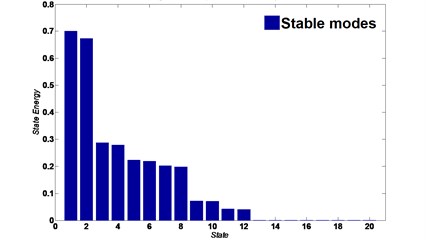
Fig. 5 shows the response spectrum of the open-loop full-order model (OLFOM) to input forces as compared to the actual response of the pipe. It is clear from the Figure, that both Modal frequencies and mode shapes poorly match actual ones. Fig. 6 however, shows that when the LQG servo control is utilized, the closed-loop full-order system (CLFOM) performs better, with clear improvement in estimating modal parameters and mode shapes. Nonetheless, amplitude discrepancies as well as modes that are not in the direction of measurement still appear in the estimates although they might not be detected by actual accelerometer measurement. The tuning values of CLFOM are, ${\mathbf{Q}}_{LQR}=1\times {10}^9\times {\mathbf{I}}_{N\times N}$, ${\mathbf{R}}_{LQR}=1$, ${\mathbf{Q}}_w=1\times {10}^9$ and ${\mathbf{R}}_v={\mathbf{I}}_{3\times 3}$, where $\mathbf{I}$ is the identity matrix. Further improvement to the model is carried out using model reduction based on SVD. To that effect, Hankel Singular Values (HSV) are calculated for the full order model which has a total of 20 states as presented in Fig. 7. The latter shows that only eight states have significant contribution to the response in the direction of measurement, at the three prescribed locations where the output is desired. Therefore, it was found that any state with HSV less than 10 % of the highest value are eliminated without any tangible effect on the accuracy of the model. The closed-loop servo controlled reduced-order model (CLROM) is implemented and the response spectrums at the Right, Middle and Left accelerometer locations are plotted in Fig. 8, this shows that the CLROM outperforms both OLFOM and CLFOM since higher order modes are treated as noise in the CLROM. The values of the estimated Modal frequencies using the CLFOM and CLROM are compared to the actual ones as listed in Table 4, which shows zero estimation error when CLROM is used. The LQG tuning values in this case are, ${\mathbf{Q}}_{LQR}=1\times {10}^6\times {\mathbf{I}}_{r\times r}$, ${\mathbf{R}}_{LQR}=\text{10}$, ${\mathbf{Q}}_w=1\times {10}^6$ and ${\mathbf{R}}_v={\mathbf{I}}_{3\times 3}$, where $\mathbf{I}$ is the identity matrix.

Fig. 5Spectrogram of actual vs. estimates of acceleration using full-order model without control

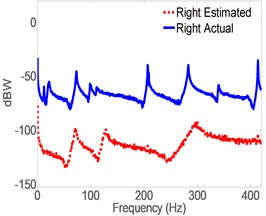
a) Right accel

b) Middle accel

c) Left accel

Fig. 6Spectrogram of actual vs. CLFOM acceleration estimates

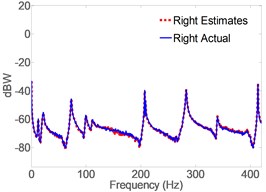
a) Right accel

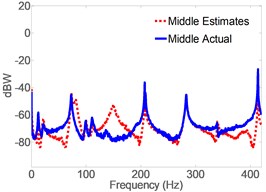
b) Middle accel

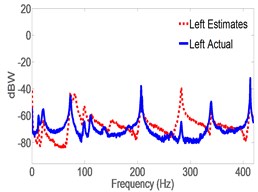
c) Left accel

Fig. 7Hankel singular values of full-order modal model in y-direction

4.3. Relating changes in structural parameters to modal frequencies shift

The effect of changes in structural parameters on Modal frequencies is examined experimentally based on the two targeted outcomes listed in Section 4.1. All previous simulation results are related to the “healthy” or unaltered pipe. To examine the effect of structural damage on Modal frequencies, a mass block (MB) is retrofitted to the pipe to mimic structural damage such as pipe scale. The pipe retrofitted with the MB is referred to as “damaged” pipe. Further, the effect of damage location relative to sensor location is also tested by varying the MB distance from the feedback sensor along the pipe span. The Right accelerometer measurement is used as the feedback signal to the CLROM and estimates, rather than actual measurement, are used to predict damage. Estimates at the Middle and Left accelerometer locations are generated by the CLROM and frequencies shift in the estimates spectrum, if any, are evaluated, keeping in mind that actual acceleration measurements at the Middle and Left locations are used only to assess the accuracy of CLROM estimates. The MB has a mass of 5.3 kg which is 20 % of the total mass of the pipe. This choice of a relatively high value for the mass block is aimed at eliminating any possibility of experimental error arising from using a smaller mass. To examine the effect of the location of the MB relative to the feedback accelerometer of the Modal frequencies shift, two cases are examined where in Case I the MB is attached at the Left location while in Case II the MB is attached at the middle as shown in Fig. 9. Experiments are carried while using the values of LQG gains for CLROM tuned for the healthy pipe such that Modal frequencies shift predicted by Eq. (23) is examined. The following presents experimental validation of the proposed method.

Fig. 8Spectrogram of actual vs. estimates generated by CLROM

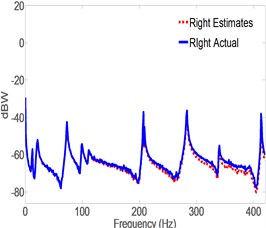
a) Right accel

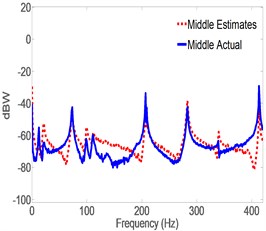
b) Middle accel

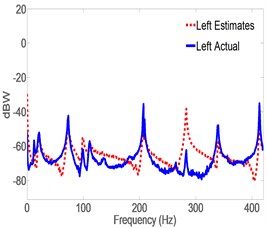
c) Left accel

Fig. 9Mass block attached to the pipe

a) MB attached at left “Case 1”end

b) MB attached at the middle “Case I1”

4.3.1. Case I: MB attached at the left

In this case, MB was attached to the pipe in the vicinity of the Left accelerometer and acceleration is estimated by CLROM at both left and middle locations. The feedback to the servo controller is the actual acceleration measured by the Right accelerometer. Fig. 10 shows that, estimates of acceleration of the damaged structure have good match to experimental ones and the closed loop system is able to estimate the vibration signature fairly accurately without re-tuning the LQG gains to match the damaged structure. Fig. 11 shows a comparison between estimated acceleration spectrum for both healthy and damaged pipes in which it is clear that shifts are significant in Modal frequencies of Modes 3, 6 and 8, and 9 and 10, as predicted by Eq. (23). Examining the mode shapes of Fig. 11 shows that all the mode shifts are detected in modes that have large displacements in the $y$-direction (i.e. perpendicular to the ground) which is the direction of acceleration measurements. This also validates the effectiveness of the model reduction technique which eliminated all the modes that have minimal contribution to the response in the $y$-direction. Notice that the remaining modes are predominantly in the lateral and horizontal directions, thus sift in their Modal frequencies is minimal in the vertical direction. It should be noticed that in Fig. 11(a), the spectrum is based on actual measurement for both Healthy and damaged because the right accelerometer measurement is available. However, Fig. 11(b) and 11(c) are obtained from estimates only, and thus the shift appearing in Fig. 11(b) and 10(c), are the estimated ones. Table 5 lists the Modal frequencies shift(s) as calculated from the actual Right acceleration measurement’s spectrum in the $y$-direction.

Fig. 10Damaged pipe acceleration estimates vs. actual using CLROM

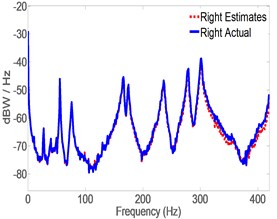
a) Right end of the pipe

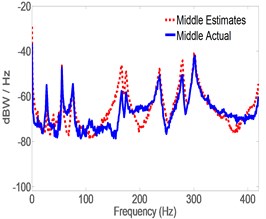
b) Middle of the pipe

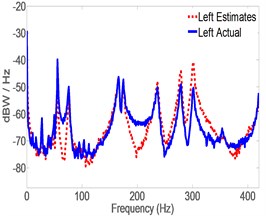
c) Left end of pipe

Fig. 11Spectrum of acceleration estimates for healthy and damaged pipes in y-direction. MB at the left location

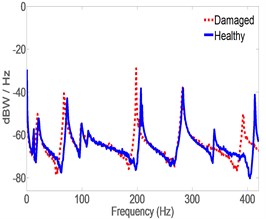
a) Right

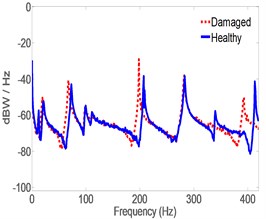
b) Middle

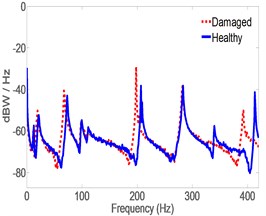
c) Left

Results in Tables 5 and 6 indicate that Modal frequencies found from actual acceleration measurements at the Right are in good agreement with those found from estimates at the Middle and Left. It also shows that the shifts found from estimates are almost identical to those found from actual measurements which is an indication that acceleration estimates are just as reliable as actual ones as per the approach proposed in this work. Fig. 11 and Tables 5 and 6 also indicate that changes in structural parameters can be detected from Modal frequencies estimates using the proposed method. The experiment was replicated three times and the outcome was similar to the results presented, each time. It is worth mentioning that all frequency shifts where towards the left of the graph indicating a drop in the Modal frequencies. This is in-line with expectations since mass was added to the structure. It can also be concluded that a change in stiffness due to cracks or loss of structural continuity would cause a shift in Modal frequencies in the direction of reduced stiffness.

Table 5Modal frequencies shift in the y-direction found from right acceleration spectrum. MB at left

Eigen frequency	$f_i$ (Hz)		${∆f}_i$ (Hz)	${∆f}_i/f_i\left(healthy\right)$
	Healthy	Damaged	Right Accel.	×100%
$f_1$	12.69	11.727	–0.963	–7.5
$f_2$	21.508	19.532	–1.976	–9.186
$f_3$	73.264	67.383	–5.8804	–8
$f_4$	99.6425	98.6712	–0.9713	–1
$f_5$	111.3288	111.3592	–0.0304	0
$f_6$	207.0272	198.2618	–8.7655	–4.23
$f_7$	208.9842	203.1541	–5.8301	–2.7
$f_8$	283.2330	282.2200	–1.0130	–0.5
$f_9$	339.8457	0	–339.84	–100
$f_{10}$	413.0762	392.1661	–20.910	–5

Table 6Eigen frequency shifts in the y-direction. CLROM estimates at middle and left acceleration spectrums. MB at left

Eigen frequency	$f_i$ (Hz) middle		${∆f}_i$ (Hz)	${∆f}_i/f_{iM}$	$f_i$ (Hz) left		${∆f}_i$ (Hz)	${∆f}_i/f_{iL}$
	Healthy	Damaged	Middle estimate	×100 %	Healthy	Damaged	Left estimate	×100 %
$f_1$	12.681	11.730	–0.9517	–7.505	12.6918	11.7047	–0.9871	–7.784
$f_2$	21.477	19.573	–1.9034	–8.863	21.474	19.525	–1.9488	–9.074
$f_3$	73.343	67.3069	–6.0366	–8.231	73.317	67.352	–5.9645	–8.132
$f_4$	99.692	98.7137	–0.9789	–0.982	99.6183	98.612	–1.0061	–1.009
$f_5$	111.4396	111.3580	–0.0816	–0.073	111.331	111.619	0.2874	0.258
$f_6$	207.1153	198.2019	–8.9134	–4.304	207.0711	198.276	–8.7950	–4.246
$f_7$	209.025	203.1134	–5.9119	–2.828	209.0186	203.176	–5.8424	–2.795
$f_8$	283.157	282.268	–0.8889	–0.314	283.1828	282.1433	–1.0395	–0.367
$f_9$	339.936	0	–339.936	–100	339.939	0	–339.939	–100
$f_{10}$	413.1300	392.602	–20.5277	–4.969	413.024	392.479	–20.5445	–4.973

4.4. Results analysis

Experimental results have shown that adding MB to the structure has caused modal frequencies shifts in some modes while suppressing other modes. For example Mode 9 in Table 6 and Mode 7 in Table 8 have disappeared when MB was attached to the pipe. This is so because the structural parameters have changed, although the change was a localized one. Modes affected by the addition of MB are those having a mode shape involving bending the $y$-$z$ plane such as Modes 3, 6, 7 and 10. Other modes affected are the ones involving rotation about $z$-axis such as mode 8 and 9. It is noticed also that higher order modes are affected more than lower order modes, for example the shift in Mode 10 is –51.67 Hz. The effect of MB on the frequency shift of Mode 10 was half of that when MB was placed at the Left because it was place very close to the modal node.

Fig. 12Spectrum of acceleration estimates for healthy and damaged pipes in y-direction. MB at the middle location

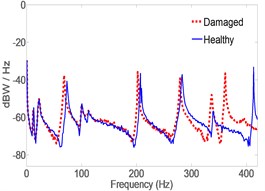
a) Right

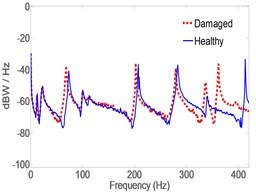
b) Middle

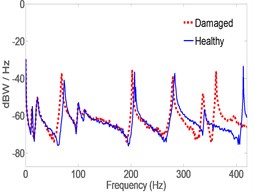
c) Left

It is also clear from the Tables 5-8 that the distance between the localized damage and the feedback sensor has affected the spectrum in different ways and thus, in addition to detecting the damage, this method can be used to detect location of the damage relative to the feedback sensor(s), which is important since limited number of sensors are needed for the CLROM. The manner by which the type of damage and its distance from the sensor is determined is not discussed in this research work due to random nature of failure, which will require extensive statistical analysis of the results presented in this work. The distribution of power into frequency components of the signal (Amplitudes) in Fig. 11 and 12 are not discussed in this work but can be utilized as an added indication of the type of damage inflicted on the structure. The reason for not taking the amplitudes into consideration is that the excitation force applied to the structure was applied manually which made it difficult to replicated test conditions. Modal damping is not considered since damping has not been explicitly altered in the experiment. Anti-resonance or zeros of the system has shown shifts as well since the feedback signal location and locations of estimates are at different distances from modal nodes. This work only considered the first ten modes of vibration to construct the state-space model from FEA data. It is well known that the number of modes retained should be determined based on the modal effective mass rather than lower order modes. However, the proposed method can be easily extended to include modes that have a 90 % or more total effective modal mass participation. Therefore, including more modes into the model before reduction will not have any effect on the functionality and the integrity of the proposed method.