Abstract
Shape coefficients of a single traverse and twin branch lines are examined through wind tunnel experiments and numerical simulations under different angle of attacks and wind speeds. It was found that the shape coefficient at angle of attack equaling to 0 is obviously smaller than the others. And the effects of Reynolds number are also large. The numerical results give difference between cases reaching 20 %, however, the experimental ones only 1.17 %. It is because that the initial condition of CFD is idealized but the wind tunnel experiment is closer to the reality.
1. Introduction
Wire shape coefficients is an important parameters for the wire wind load calculation, design technical specification recommends adopting the empirical values, and whether there is interference effect in multi-split wires, the difference with empirical values needs to be further clarified. In this paper, shape coefficients of double split wire arrangement are studied. Wind tunnel experiments and CFD numerical simulations are carried out on double split wire respectively.
2. Wire shape coefficients wind tunnel experiment
Wire experiment tests shape coefficients of a single traverse and twin branch lines respectively. The working conditions of a single traverse experiment are divided into four parts:1) uniform flow field measurement under 10 m/s wind speed; 2) uniform flow field measurement under 20 m/s wind speed; 3) turbulent flow field measurement under 10 m/s wind speed;4) turbulent flow field measurement under 20 m/s wind speed. Wind direction of twin branch lines varies from 0 degrees to 90 degrees, with a change of 10 degrees per interval. The definition of wind direction is shown in Fig. 1.
Fig. 1Schematic diagram of inflow wind direction angle of double split wires

a) 0°
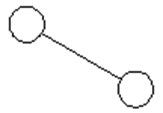
b) 30°
c) 90°
The length of different test model is about 80 cm, and the installation of the processed well wires in wind tunnel is shown in Fig. 2. When installed in wind tunnel, the wires model is fixed on the balance by the base. In order to avoiding the test accuracy is affected through fixed base bears wind load directly, above the fixed base, the circular plate and diversion slope are used to cover the force measuring balance base and connecting member.
Fig. 2Installation schematic diagram of wire model in wind tunnel: a) single wire, b) double wire

a)

b)
Shape coefficients comparison of the wire tested in uniform flow field and turbulent flow field is shown in Table 2. It can be seen that the shape coefficients of single wire under 10 % turbulence level measured by wind tunnel test is smaller than that under uniform flow field, overall smaller about 1 %-5 %.
Table 2Comparison of shape coefficients of wire under uniform flow and turbulent flow
Wind speed (m/s) | single wire | Deviation (%) | |
Uniform flow | Turbulent flow | ||
10 | 1.1486 | 1.1353 | 1.16 |
20 | 0.972 | 0.9196 | 5.4 |
3. CFD simulation calculation of wire shape coefficients
3.1. Mesh generation
In this project, O-type grid is adopted to deal with boundary grid. In order to ensure the dimensionless height of wall 1, the first layer grid of near wall must be estimated before calculation. In order to meet this requirement, we can calculate the height of the first boundary layer before dividing grid by the following formula:
where is the height of the first boundary layer grid needed, and the value of this section is 1. The grid growth rate of the calculation is 1.15, and the number of grids is 25000, the grid distribution is shown in Fig. 3 to Fig. 5.
Fig. 3Grid distribution diagram of a single traverse
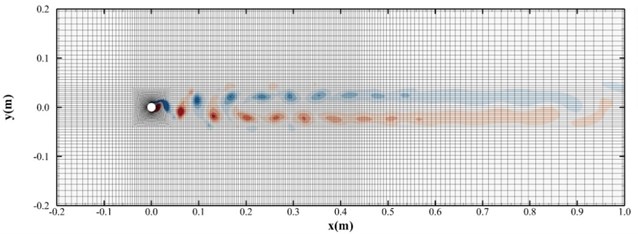
Fig. 4Grid distribution diagram of series twin branch lines
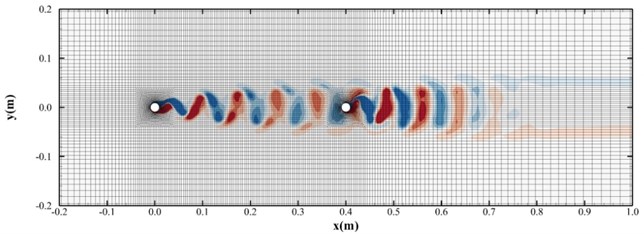
Fig. 5Grid distribution diagram of parallel twin branch lines
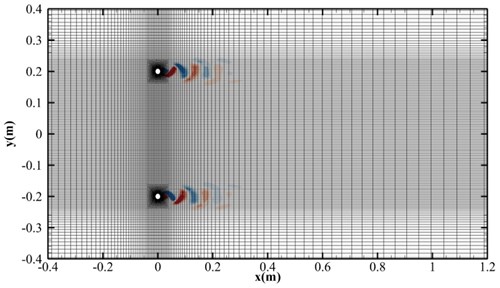
3.2. Calculation conclusion
At the time of analysis, the aerodynamic time history of the whole coordinate system , and is directly output, so it can be directly transformed into the mean aerodynamic force coefficient under the whole coordinate system (body axis). Define the ratio of shape coefficients of a single traverse to coefficient of multi-split wires to indicate proportional relationship between drag resistance of multi-split wires and a single traverse under the same wind speed, following formula:
Table 3Wire shape coefficient table
Wire type | Wind speed (m/s) | Inflow condition | Wire | ||
A single traverse | 10 | Non turbulent flow | \ | 1.16 | \ |
Turbulent flow | \ | 0.82 | \ | ||
Series twin branch lines | 10 | Non turbulent flow | 1# | 1.18 | 1.02 |
2# | 0.21 | 0.21 | |||
Turbulent flow | 1# | 0.84 | 1.03 | ||
2# | 0.73 | 0.72 | |||
Parallel twin branch lines | 10 | Non turbulent flow | 1# | 1.17 | 1.01 |
2# | 1.17 | 1.16 | |||
Turbulent flow | 1# | 0.82 | 1.00 | ||
2# | 0.82 | 0.82 |
4. Conclusions
In this paper, the wind tunnel experiments on shape coefficients of a single traverse and twin branch lines are carried out, and the CFD simulation is compared and analyzed, so the following conclusions are obtained:
1) The shape coefficient at angle of attack equaling to 0 is obviously smaller than the others, because the shielding effect of upstream wire to downstream wire is the most obvious at angle of attack equaling to 0, and that almost disappeared at angle of attack equaling to 10; The shape coefficient of twin branch lines under 20 m/s wind speed is smaller than that under 10 m/s wind speed, which is consistent with the test result of a single traverse, mainly because of the change of Reynolds number caused by the change of wind speed.
2) Comparing the wire shape coefficient measured by wind tunnel experiment and that calculated by numerical CFD can be seen, 10 m/s wind speed, the shape coefficients deviation of a single traverse measured by wind tunnel experiment under different flow fields is 1.17 %, and the calculated deviation of CFD value reached 20 %, in other conditions, there are different degrees deviation.
References
-
Sun Qigang, Xie Qiang Wind tunnel test study on shielding effect of tandem double split conductors. Electric Power Construction, Vol. 34, Issue 10, 2013, p. 6-11.
-
Sun Qigang, Xie Qiang, Ren Yongyi, et al. Evaluation of shielding effect of multi split wires in wind tunnel test. Journal of State Grid Technology Institute, Vol. 18, Issue 1, 2015, p. 1-9.
-
Zhang Suxia, Liu Xijun, Li Wei Study on variation law of wind load on four bundled wires. Engineering Mechanics, Vol. 30, Issue 6, 2013, p. 321-326.
-
Cai Mengqi, Yan Bo, Liu Xiaohui, et al. Analysis of wind resistance coefficient of multi bundle wires. Journal of Chongqing University, Vol. 36, Issue 1, 2013, p. 110-114.
-
Min Xuan, Niu Huawei, Wen Zhike, et al. Experimental study on wire shape coefficient. China Power, Vol. 49, Issue 5, 2016, p. 171-177.
-
Cheng Tian, Liu Xiu Analysis of shape coefficient of multi bundled wires. Yunnan Electric Power Technology, Vol. 44, Issue 6, 2016, p. 29-30.
-
Xie Qiang, Guan Zheng Shield effect of resistance coefficient of eight split wires wind tunnel experiment. Chinese Journal of Electrical Engineering, Vol. 19, 2013, p. 149-156.
-
Zuo Taihui, Niu Huawei, Min Xuan, et al. Study on interference effect of drag coefficient of mean wind load on bundled wires. Experimental Fluid Mechanics, Vol. 29, Issue 2, 2015, p. 37-42.
-
Xie Qiang, Sun Qigang, Guan Zheng Study on wind tunnel experiment of integral resistance coefficient of multi split wires. Power Grid Technology, Vol. 37, Issue 4, 2013, p. 1106-1112.
