Research on consumption prediction of spare parts based on fuzzy C-means clustering algorithm and fractional order model

1. Introduction

In the analysis of vibration abrasion, noise factor is a significant aspect to reduce the prediction accuracy. In order to discard noise in signal, scholars domestic and abroad have carried on many years of research, and the de-noising methods such as Fourier transform [1-3] and wavelet transform [4, 5] were proposed. However, although the stationary signal can be de-noised by Fourier transform well, but this method can hardly identify the high frequency part and noise of the signal, which is not conducive to the analysis of non-stationary signals. Compared with the Fourier transform, the wavelet transform can improve the performance of de-noising of non-stationary nonlinear time-varying signals, but the effect of wavelet filtering is unsatisfactory when the noise is large, or the energy is limited, and also the wavelet basis is not easy to select.

For improving the situation mentioned above, a fuzzy C-means clustering algorithm was established. After distinguishing large scale noise and sharp features, fuzzy C-means clustering algorithm was utilized to cluster the sharp features and obtain more accurate data. Besides, considering the characteristics of less samples, the fractional order cumulative model was established to reduce the perturbation bounds and improve the stability of the prediction model.

2. Fuzzy C-means clustering algorithm

Fuzzy C-mean clustering (FCM) is a method which utilizes the membership degree to determine the degree of each data point belonging to a certain cluster. A set of data can be divided into two or more cluster centers by FCM. Suppose that $P=\left\{p_1,p_2,\dots ,p_N\right\}$ is a set of data points with $s$dimensional which contains$N$data points. Then the set can be divided into $C$ clusters: $V=\left\{v_1,v_2,\dots ,v_C\right\}$, where $v_i$ is center of the cluster. Thus, the objective function of the fuzzy C-means clustering algorithm is defined as:

where:

$u_{ki}$ – The membership degree of data point $p_k$ relative to cluster center $v_i$;

$m$ – Fuzzy control degree parameter;

$d_{ki}^2\left(p_k,v_i\right)$ – Euclidean distance between data point $p_k$ and cluster center $v_i$, and $d_{ki}^2\left(p_k,v_i\right)={‖p_k-v_i‖}^2$.

The constraints of Eq. (1) are as follows:

In order to reflect the influence of different data points, the improved fuzzy clustering method was established, which defined the fuzzy weight coefficient $\omega$ of fuzzy weight distance, based on the different contribution of different data points to the same cluster center. And then the distance between the data points $p_k$ and the cluster centers $v_i$ is defined as:

In contrast, the fuzzy weight coefficient makes the distance farther more farther and closer, which can reduce the influence of noise, and make the clustering results better.

The basic steps of the algorithm are as follows:

1) Set the radius of the bounding sphere is $R$, and the threshold $\xi$ of the number of data points in the sphere is determined according to the density of the point cloud;

2) Select a data point $p_k$ and calculate the number of the adjacent points $\epsilon$ in the sphere enclosed of which the center is $p_k$ and the radius is $R$;

3) Compare the number of data in sphere enclosed and the threshold value $\xi$, if $\epsilon <\xi$, the data point would be determined as noise and deleted directly;

4) If $\epsilon \ge \xi$ the data point $p_k$ is regarded as the qualified point, the improved FCM algorithm is utilized to cluster the enclosing sphere contains $p_k$. Meanwhile, the data in the cluster is recorded, and all data in the sphere will be replaced by the data of the cluster center;

5) Return to step (2) and determine the remaining points in turn.

3. Fractional order model

In order to define the fractional order operation, the ascending order function was introduced:

where $\left[\begin{array}{l}x\\ 0\end{array}\right]=$ 1.

The fractional cumulative grey model $GM\left(r,1\right)$ is obtained after making the order of $GM\left(p,1\right)$ extended to the general positive real number $r$. Then $C_{k-i+p-1}^{k-i}$ can be obtained by combining with Eq. (1):

Make $p$ extended to $r$ which is general positive real number and $r\in {\mathbf{R}}^{+}$. The $r$ order cumulative generating series can be defined as:

When $r\in \left(0,+\infty \right)$, $x^{\left(r\right)}\left(k\right)$ is $r$ fractional order accumulation, which can be written in matrix form:

where:

${\sum }_r‍$ is $r$ fractional order cumulative matrix.

Similar to the integer order cumulative matrix, the transposed matrix of ${\sum }_r‍$ is a $r$ fractional Inverse cumulative matrix.

The reverse fractional order cumulative generation of series can be obtained by ${\mathbf{X}}^{\left(r\right)}={\mathbf{X}}^{\left(0\right)}{\left({\sum }_r‍\right)}^T$, then the reverse cumulative gray model $GOM\left(r,1\right)$ can be established.

The discrete form of fractional order model $GM\left(r,1\right)$ can be expressed as:

where $r\in \left(0,+\infty \right)$.

Because $det\left({\sum }_r‍\right)=1\ne 0$, so the ${\sum }_r‍$ is nonsingular matrices. Therefore, the ${\sum }_r^{-1}$exists, and ${\sum }_r‍·{\sum }_r^{-1}={\sum }_r^{-1}·{\sum }_r‍=\mathbf{I}$, where $\mathbf{I}$ is unit matrix.

4. Numerical example

As shown in Table 1, in order to verify the validity and reliability of the established hybrid model, the data from [6] was used as original signal for analyzing.

4.2. Simulation

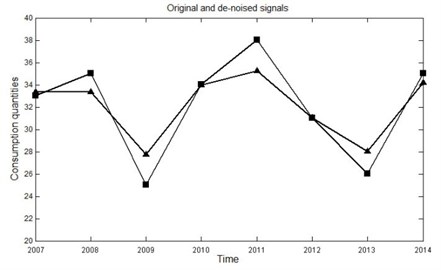
In order to eliminate the influence of noise in the series, the original data was utilized as input to Fuzzy C-means clustering algorithm. Before the prediction, the residual was discarded, and the de-noised data were constructed by FCCA. The original data and the de-noised data were shown in Fig. 1.

Fig. 1The de-noised and original consumption data

The prediction model was established by fractional order grey model GM($r$,1) and the optimal order $r$ was 0.703, which calculated by genetic algorithm. And then the prediction results of de-noised signal were calculated. Moreover, for facilitate analyzing the predictive capabilities of FCCA-FOM, GM(1,1), FOM model and EWT-BP neural network were employed for comparison. The relative error and mean relative error(MRE) were utilized to measure the forecasting accuracy, and the results were shown in Table 2.

Table 2The prediction results and performance evaluations of forecasting results by different models

Time and MRE	Actual data	FCCA-FOM		GM(1,1)		FOM		EWT-BP neural network
		Prediction data	Relative error/%	Prediction data	Relative error/%	Prediction data	Relative error/%	Prediction data	Relative error/%
2007	33	32.1	–2.73	35.9	8.79	36.7	11.21	34.6	4.85
2008	35	36.5	4.29	33.3	–4.86	33.4	–4.57	36.9	5.43
2009	25	25.9	3.60	27.1	8.40	26.5	6.00	26.3	5.20
2010	34	35.5	4.41	32.1	–5.59	31.7	–6.76	36.1	6.18
2011	38	39.4	3.68	40.3	6.05	39.8	4.74	36.4	–4.21
2012	31	30.3	–2.26	28.8	–7.10	29.9	–3.55	29.5	–4.84
2013	26	27.5	5.77	28.9	11.2	29.1	11.92	27.6	6.15
2014	35	35.8	2.29	36.9	5.43	37.5	7.14	36.5	4.29
2015	36	36.9	2.50	38.6	7.22	38.8	7.78	37.7	4.72
MRE /%		3.50		7.18		7.07		5.10

5. Conclusions

Considering the noise in consumption series, a hybrid forecasting method combining FCCA and Fractional order was proposed, which can eliminate the noise in the original series and improve the prediction accuracy. At the same time, the method requires less data and no complicated integral calculation, which is easier to implement and convenient for engineering application. The numerical example showed that the relative error and average relative error of FCM-FOM model are less than GM(1,1), FOM and EWT-BP neural network, which reflect the accuracy of the model established.