Aerodynamic admittance influence on buffeting performance of suspension bridge with streamlined deck

Gang, Yao; Yang, Yang; Bo, Wu; Lianjie, Liu; Liangliang, Zhang

doi:10.21595/jve.2018.19681

Journal of Vibroengineering

Browse Journal

Submit article

Published: 15 February 2019

Check for updates

Aerodynamic admittance influence on buffeting performance of suspension bridge with streamlined deck

Yao Gang¹

Yang Yang²

Wu Bo³

Liu Lianjie⁴

Zhang Liangliang⁵

^{1, 2, 3, 5}Key Laboratory of New Technology for Construction of Cities in Mountain Area, Ministry of Education, Chongqing, China

⁴Department of Highway Engineering, Chongqing Construction Science Research Institute, Chongqing, China

^{4, 1, 2, 3, 5}School of Civil Engineering, Chongqing University, Chongqing, China

Corresponding Author:

Yang Yang

Cite the article Download PDF

Downloads 1762

WoS Core Citations 10

CrossRef Citations 9

Abstract

Buffeting performance is growing sensitive to external and internal factors with increasing span of bridge. Aerodynamic admittance is an essential parameter in analyzing buffeting performance. In this paper, aerodynamic admittance in different conditions were conducted in wind tunnel tests by section model. Three kinds of aerodynamic admittance functions were used to calculating buffeting performance respectively. It is found that the aerodynamic admittance of streamlined deck is closely related to wind attack angle, and has a small difference at different wind speeds. However, the influence of aerodynamic admittance on buffeting performance is affected by the wind speed significantly. Under given conditions, adopting the Sears function as the admittance function of a similar streamlined box girder is reasonable, while the buffeting performance result obtained by adopting an admittance function as 1.0 is very conservative.

1. Introduction

Buffeting performance is a forced vibration caused by turbulence wind. This vibration can interfere many features of bridge, such as fatigue damage, discomfort for vehicles and pedestrians. Buffeting performance is growing sensitive to external and internal factors with increasing span. Researchers have been working in external factors influence on buffeting performance, including topography [1], extreme value of typhoon [2], turbulence characteristics [3], turbulent spatial correlation coefficient [4], skew wind [5-7], design and measured power spectrum [8], non-stationary and stochastic excitation [2, 9-11]. There are also a multitude of researchers working in internal factors simultaneously, including multiple tuned mass dampers [12-15], mechanically driven flaps [16-18], mid-tower [19], catwalk [20], central buckle [21], and slotted deck [22]. Study method makes varied with a tendency more proper to reality, with improved analysis theories in buffeting performance, such as linear regression [6], non-linear regression analysis [21], evolutionary power spectral density [19, 23], varying frequency-increment sweeping method [10], and three-dimensional simulation [24, 25]. Researches above demonstrate that the buffeting performance is becoming an extremely refined analysis. Aerodynamic admittance is of great importance in the evaluation of the buffeting and response of structures. Buffeting performance with considering of aerodynamic admittance can reflect the vibration of bridge more closely to reality and meet the requirement of refined analyses. However, a handful of research is concentrated in aerodynamic admittance effect. Wang H. [7] compared two types of aerodynamic admittance function, 1.0 and Sear functions, in calculating the buffeting performance. Tubino F. [26] introduced a generalized quasi-static theory, defining new relationships among the flutter derivatives and the aerodynamic admittance functions. Costa C. [27] numerically evaluated aerodynamic admittance functions for rectangular sections and compared with experimental and analytical results. Massaro M. [28] investigated the effect of aspect-ratio on the aerodynamic admittance of thin aero foils, flat plates and thin bridge section. Hejlesen M. M. [29] estimated the aerodynamic admittance of bridge sections by mesh-free vortex method and confirmed its feasibility by comparing to available wind tunnel data. Zhao L. [30] proposed a new identification algorithm about the admittance function and validated it by a comparison between the numerical calculation and wind tunnel tests. Hua X. G. [31] developed an improved perturbation method for the statistical identification of structural parameters by using the measured modal parameters with randomness.

The buﬀeting performance is of great importance during the service period of long-span bridges, aerodynamic and dynamic characteristics could directly contribute to the buﬀeting performance. For the aerodynamic characteristics, the most important factor may be the aerodynamic admittance as it reﬂects the unsteady features in buﬀeting forces. Influence of aerodynamic admittance on buffeting performance is still inadequate. Researches above paid particular emphasis on exploring typical aerodynamic admittance function, such as Sear function, Davenport function. There is rarely research about influence of measured aerodynamic admittance on buffeting performance. The buffeting performance considering measured aerodynamic admittance are closer to practical situation.

In this study, aerodynamic admittance in different conditions were conducted in wind tunnel tests by section model. Aerodynamic admittance functions were deduced. Three type aerodynamic admittance functions were used to calculate buffeting performance respectively in time domain, which accounted for structural nonlinearities. Taking the Cuntan Yangtze bridge as an example, the differences of buﬀeting performance with three kinds of aerodynamic admittance functions were analyzed in time domain via a suspension bridge model built on ANSYS platform. Effects of aerodynamic admittance on buﬀeting performance of bridge were summarized. The analytical results are expected to provide references for the buﬀeting performance analysis, fatigue damage and comfort of wind-vehicle-bridge system analysis.

2. Description of wind tunnel test

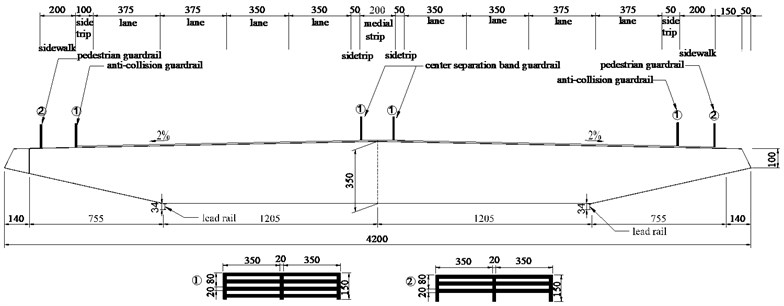
Cuntan Yangtze bridge is taken as the project background. The main girder is a streamlined closed, flat box girder. Width of the deck section is 42.0 m and thickness of the section is 3.5 m. Attachment structures have a strong influence on aerodynamic characters. Therefore, guardrails and lead rails are considered in wind tunnel test. Bridge section model includes pedestrian guardrail, anti-collision guardrail, center separation band guardrail and lead rail, and the detail dimensions are shown in Fig. 1.

Fig. 1Dimensions of standard cross section (cm)

In order to get the static force coefficients and aerodynamic admittances of real bridge, two bridge section models were used in wind tunnel test. Aerostatic coefficients were tested by subsection elastic model in first test section of wind tunnel, which were used to calculate aerostatic load in buffeting performance. Aerodynamic admittances were measured by subsection rigid model in the second test section of wind tunnel.

2.1. Description of subsection elastic model

Subsection elastic model was made of wood. Pedestrian guardrails, anti-collision guardrails and center separation band guardrails were manufactured in plastic plates by machine. The subsection elastic model had a scalar of 1/60 to the real bridge section, and it was shown in Fig. 2. Wind tunnel test requires that the subsection elastic model is similar to the real bridge in geometric dimensions, as well as frequency and damping ratio. But actually, the subsection elastic model is not exactly the same with real bridge in all aspects. Deviation is allowable in the wind tunnel test. Allowable damping ratio deviation should be controlled less than 10 % and allowable deviation of frequency, mass should be controlled less than 3.0 %. From Table 1, it can be calculated that the deviation is 4.3 % on vertical bending damping ratio and 3.8 % on torsion damping ratio, and other parameters kept the same as prototype model. As a consequence, subsection elastic model can meet the demand of experiment.

Fig. 2Subsection elastic model

Table 1Design parameters of section elastic model

Parameter	Unit	Actual value	Required value	Value in test
Height	m	3.5	0.0583	0.0583
Width	m	42.0	0.7	0.7
Linear mass	kg/m	27600	7.667	7.667
Linear mass moment of inertia	kg·m²/m	5137700	0.3987	0.3987
Vertical bending frequency	Hz	0.174	2.216	2.216
Vertical bending damping ratio	%	0.5	0.389	0.372
Torsion frequency	Hz	0.39726	5.404	5.404
Torsion damping ratio	%	0.5	0.439	0.422

2.2. Description of subsection rigid model

The subsection rigid model was made up of measured section and compensation section was shown in Fig. 3. The subsection rigid model had a ratio of 1/300 with the real bridge section. The model was made from light and thin-walled wood material and possessed enough stiffness avoiding deformation and vibration in the test. A square steel frame was fixed in wind tunnel floor and an aluminum bar in the middle of the frame beam was vertically mounted to fix the compensation section. Compensation section was installed in the aluminum bar and had a space less than 2.0 mm with the measuring section. The importance of three-dimensional effects was aspect-ratio dependent (neglecting any end effect). The results obtained on a rigid span were confirmed when considering a flexible span. The subsection rigid model was tested after installation, and the basic frequency of wide-body flat steel box girder in-plane was 56.0 Hz, out-of-plane basic frequency was 35.0 Hz, reverse fundamental frequency was 81.0 Hz. All frequency was much larger than the measurement band of buffeting aerodynamics. Consequently, the system can meet the requirements of a high frequency force measuring test. The sampling frequency adopted for aerodynamic force was 100.0 Hz.

Fig. 3Subsection rigid model

2.3. Description of wind tunnel

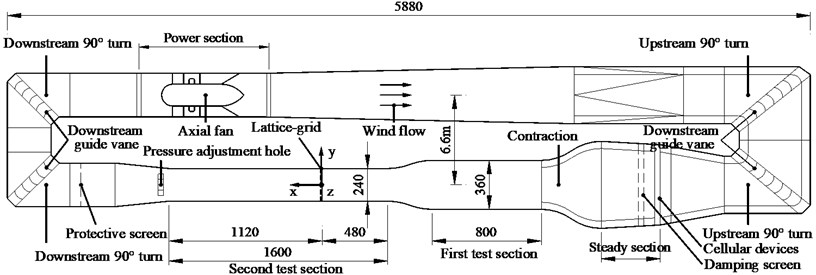
The tests were performed in XNJD-1 wind tunnel, and the geometry of wind tunnel was shown in Fig. 4. Static force coefficients were measured in the first test section and aerodynamic admittances were measured in the second test section of wind tunnel. The maximum wind velocity was 45.0 m/s and the minimum wind velocity was 0.5 m/s. Both turbulence flow less than 0.1 % and uniform flow can be generated by this wind tunnel. Lattice-grid was used to producing turbulence flow and position of lattice-grid was shown in Fig. 4. The section model was placed in the middle of the test section and it spanned all the test section width. The effect of the boundary layer was neglected.

Fig. 4Geometry of wind tunnel (cm)

Two kinds of the wind speed acquisition sensors were used. One was the hot-wire anemometry sensor shown in Fig. 5 and the other was turbulent flow instrumentation (TFI) series 100 Cobra Probe sensor shown in Fig. 6. The former was placed in the upstream with 0.4 m from the side wall and 0.2 m from the lattice-grid at the height of 0.9 m. It was used to measure the mean wind speed, with an immediately display screen outside of the wind tunnel through a small hole of the side wall, in order to show the upstream speed instantaneously. The latter was a pressure probe placed in the selected downstream monitor points behind the lattice-grid, which can provide dynamic, three-component velocities and local static pressure measurements simultaneously. The mean wind speed in the same position measured by the two kinds of sensors had been verified before the experiment.

Fig. 5Hot-wire anemometry sensor

Fig. 6TFI cobra probe

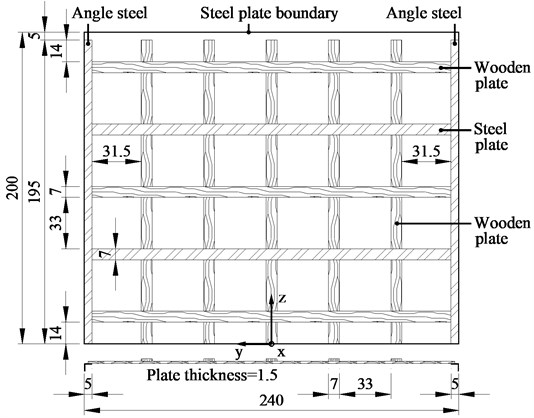
Passive lattice-grid technology is a kind of commonly used method to generate turbulent flow. Lattice-grid was adopted in the test, and the detail information was shown in Fig. 7. Both turbulence intensity and turbulence integral scale were calculated from data measured by the TFI Cobra Probe.

Fig. 7Geometry of lattice-grid (cm)

2.4. Results of aerostatic coefficients

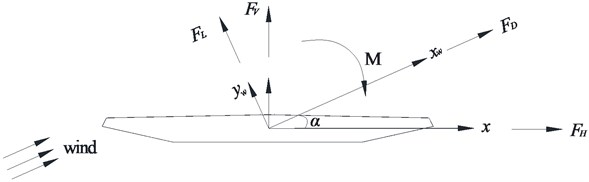
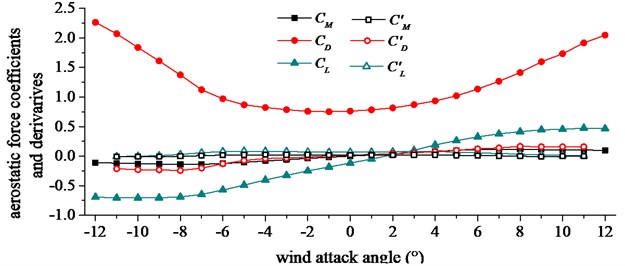
Aerostatic coefficients and its derivatives were used to calculate the buffeting loads, and they were obtained by static test in first test section of wind tunnel. Tests were done in uniform flow. Subsection elastic model was used in testing the aerostatic coefficients. Mechanical model of static force at wind axis and body axis can be shown in Fig. 8. $F_{H}$ is the lateral drag force in the conventional axis, $F_{V}$ is the vertical lift force in the conventional axis, $M$ is the moment in the conventional axis. $F_{D}$ is the lateral drag force in the wind axis, $F_{L}$ is the vertical lift force in the wind axis, $M_{Z}$ is the moment in the wind axis. $α$ is the wind attack angle. $F_{H}$ , $F_{V}$ and $M$ could be obtained directly by subsection elastic model in wind tunnel test.

Fig. 8Mechanical model of static force at wind axis and conventional axis

Forces and moments can be transformed in wind axis and conventional axis, and the relationship can be expressed in Eq. (1), Eq. (2) and Eq. (3):

1

F_{L} = - F_{H} s i n α + F_{V} c o s α,

2

F_{D} = F_{H} c o s α + F_{V} s i n α,

3

M_{Z} = M .

Aerostatic coefficients could be obtained by Eq. (4), Eq. (5) and Eq. (6):

4

C_{L} (α) = \frac{F_{L}}{0.5 ρ U^{2} B L},

5

C_{D} (α) = \frac{F_{D}}{0.5 ρ U^{2} B L},

6

C_{M} (α) = \frac{F_{M}}{0.5 ρ U^{2} B^{2} L},

where $U$ represents mean wind velocity, $ρ$ represents density of air, $B$ represents width of the bridge deck, $C_{L}$ , $C_{D}$ and $C_{M}$ represent dimensionless lift, drag and moment coefficients, $C_{L}^{'}$ , $C_{D}^{'}$ and $C_{M}^{'}$ represent derivatives of lift, drag and moment coefficients respectively. Results of aerostatic coefficients and its derivatives were shown in Fig. 9, and results at 0° wind attack angle were used in analyzing the buffeting performance of long-span bridge.

Fig. 9Aerostatic coefficients and derivatives

2.5. Results of aerodynamic admittance

Subsection rigid model was used to obtain the aerodynamic admittance in turbulent flow. The five component high frequency balance was fixed on the wind tunnel floor surface. Three component of power spectrum of turbulent wind can be respectively gotten by FFT (fast Fourier transform) with MatLab. Sensor location of TFI Cobra Probe was 2.4 m from the air grid in the horizontal direction and 0.3 m from the bottom of the wind tunnel in the vertical direction. The arrangement of aerodynamic admittance test was shown in Fig. 10. Five working conditions considered in the wind tunnel test were shown in Table 2. Comparison of results of equivalent admittance function from five repeated experiments were exhibited in Fig. 11 and fitting results of aerodynamic admittance were exhibited in Fig. 12. In the Fig. 11 and Fig. 12, the equivalent drag, lift and moment admittance were the square of the absolute value of drag, lift and moment admittance respectively, and they were the dimensionless parameters. The reduced frequency was a dimensionless parameter relating to frequency, width of bridge and wind speed.

Fig. 10Arrangement of aerodynamic admittance test (cm)

Table 2Working conditions considered in the wind tunnel test

Working condition	W8-W0	W10-W0	W12-W0	W12+W3	W12-W3
Wind speed (m/s)	8.47	10.15	12.58	12.58	12.58
Wind attack angle (°)	0	0	0	+3	–3

Comparing W8-W0, W10-W0 and W12-W0 working conditions in Fig. 11 and Fig. 12, the identification results of aerodynamic admittance had a small difference at different wind speeds. Comparing W12-W0, W12+W3 and W12-W3 working conditions in Fig. 11 and Fig. 12, the results of the equivalent admittance function had an obvious difference under different wind attack angles. No distinct relationship of admittance function following wind attack angle was found under the condition of passive incoming flow. Lift admittance was the largest in the aerodynamic admittance. Draft admittance increased obviously with the increasing of wind attack angle, and the trend of change was evident. Lift and moment admittance decreased with the increasing of wind attack angle, and the trend of change was slighter than draft admittance.

Equivalent aerodynamic admittance method was built on the improvement cross-power spectrum method [32]. Buffeting force spectrum was measured from the placed scale model with high frequency dynamic balance after the initial value checked. Turbulent wind power spectrum was measured by the TFI Cobra Probe placed in the same environment. In order to get a more accurate bridge buffeting response, aerodynamic admittance expression of wide-body flat steel box girder was presented in this paper by custom equation in MatLab with Eq. (7):

7

{|χ_{R} (k)|}^{2} = \frac{γ}{1 + β k^{δ}},

where $χ_{D u}$ , $χ_{L u}$ and $χ_{M u}$ represent draft, lift and moment admittance. Where $γ$ , $β$ and $α$ represent fitting parameters. The condition with 0° wind attack angle was the most widely used condition in many research [1-4, 8-12]. Therefore, conditions with 0° wind attack angle were chosen to fit the aerodynamic admittance expression in three directions. The fitting data of aerodynamic admittance was shown in Table 3.

Fig. 11Identification results of aerodynamic admittance

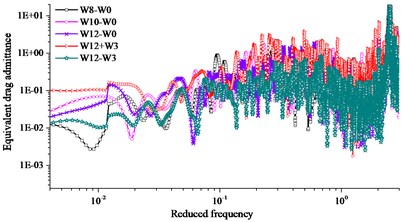
a) Equivalent drag admittance

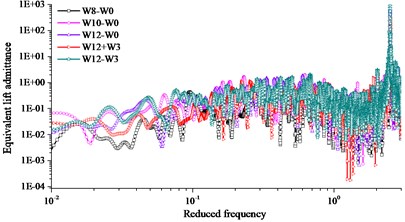
b) Equivalent lift admittance

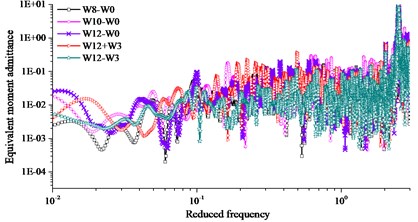
c) Equivalent moment admittance

Fig. 12Fitting results of aerodynamic admittance

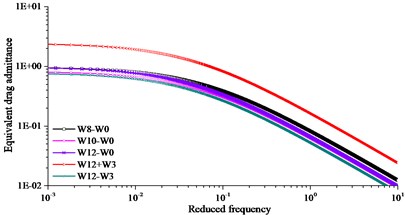
a) Equivalent drag admittance

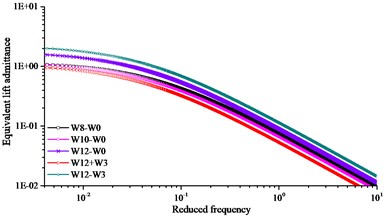
b) Equivalent lift admittance

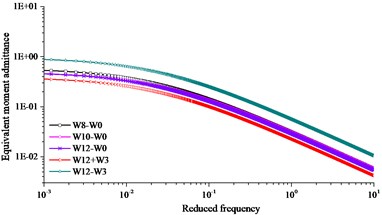
c) Equivalent moment admittance

Table 3The fitting data of aerodynamic admittance

$Χ_{R}$	$γ$	$β$	$σ$
$χ_{D u}$	1.18	12.26	0.92
$χ_{L u}$	0.62	14.13	0.75
$χ_{M u}$	0.96	8.25	0.82

3. Sectional forces in time domain

The wind load acting on bridge deck can be divided into two parts, including self-excited aerodynamic loads and turbulent loads. Buffeting loads can be expressed in Eq. (8), Eq. (9) and Eq. (10) [24]:

8

L (t) = L_{s e} (t) + L_{b} (t),

9

D (t) = D_{s e} (t) + D_{b} (t),

10

M (t) = M_{s e} (t) + M_{b} (t),

where $L_{s e}$ , $D_{s e}$ and $M_{s e}$ represent lift, drag and moment due to self-excited motions, respectively. Self-excited, and buffeting forces are shown schematically in Fig. 13.

Fig. 13Aerodynamic forces on bridge deck

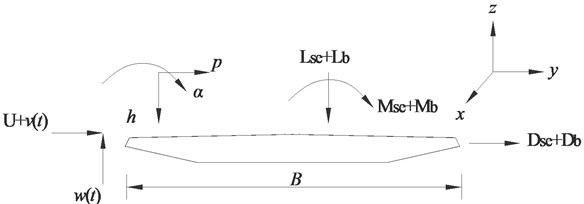
The lift, drag and moment of the self-excited part of the force at per unit length of the deck can be expressed in Eq. (11), Eq. (12) and Eq. (13):

11

L_{s e} (t) = \frac{1}{2} ρ U^{2} (2 B) [K H_{1}^{*} \frac{\dot{h}}{U} + K H_{2}^{*} \frac{B \dot{α}}{U} + K^{2} H_{3}^{*} α + K^{2} H_{4}^{*} \frac{h}{B} + K H_{5}^{*} \frac{\dot{p}}{U} + K^{2} H_{6}^{*} \frac{p}{B}],

12

D_{s e} (t) = \frac{1}{2} ρ U^{2} (2 B) [K P_{1}^{*} \frac{\dot{p}}{U} + K P_{2}^{*} \frac{B \dot{α}}{U} + K^{2} P_{3}^{*} α + K^{2} P_{4}^{*} \frac{p}{B} + K P_{5}^{*} \frac{\dot{h}}{U} + K^{2} P_{6}^{*} \frac{h}{B}],

13

M_{s e} (t) = \frac{1}{2} ρ U^{2} (2 B^{2}) [K A_{1}^{*} \frac{\dot{h}}{U} + K A_{2}^{*} \frac{B \dot{α}}{U} + K^{2} A_{3}^{*} α + K^{2} A_{4}^{*} \frac{p}{B} + K A_{5}^{*} \frac{\dot{p}}{U} + K^{2} A_{6}^{*} \frac{p}{U}],

where $ρ$ represents density of air; $B$ represents width of the bridge deck; $K$ represents reduced frequency, and $K = B ω$ / $U$ , $ω$ represents circular frequency of the bridge motion; $H i^{*}$ , $P i^{*}$ , $A i^{*}$ ( $i =$ 1, 2, 3, 4, 5, 6) represent flutter derivatives of the bridge deck measured through the wind tunnel tests shown in Fig. 4. The identified flutter derivatives were input as the coefficients in the aeroelastic stiffness and damping matrices of Matrix27; $h$ , $p$ and $α$ represent vertical, horizontal and rotational displacement of the bridge deck, respectively. Buffeting loads at per unit span length are expressed in Eq. (14), Eq. (15) and Eq. (16):

14

L_{b} (t) = \frac{1}{2} ρ U^{2} q B [2 C_{L} (θ) χ_{L u} \frac{u (t)}{U} + (C_{L}^{'} (θ)) + C_{D} (θ)) χ_{L u} \frac{w (t)}{U}],

15

D_{b} (t) = \frac{1}{2} ρ U^{2} B [2 C_{L} (θ) χ_{L u} \frac{u (t)}{U} + C_{D}^{'} (θ)) χ_{D w} \frac{w (t)}{U}],

16

M_{b} (t) = \frac{1}{2} ρ U^{2} B^{2} [2 C_{M} (θ) χ_{L u} \frac{u (t)}{U} + C_{M}^{'} (θ)) χ_{M w} \frac{w (t)}{U}],

where $L_{b}$ , $D_{b}$ and $M_{b}$ represent lift, drag and moment due to buffeting effects, respectively. $C_{L} (θ)$ , $C_{D} (θ)$ and $C_{M} (θ)$ are dimensionless aerostatic coefficients (lift, drag and moment coefficients) at a specified wind angle. $C_{L}^{'} (θ)$ , $C_{D}^{'} (θ)$ and $C_{M}^{'} (θ)$ are its derivatives. In this buffeting performance analysis, the $θ$ is defined as 0°, and the aerostatic coefficients and its derivatives are defined according to Fig. 8. $u (t)$ and $w (t)$ are wind velocity fluctuations in the horizontal and vertical directions, respectively. $χ_{L u}$ , $χ_{D u}$ and $χ_{M u}$ are aerodynamic admittance.

4. Bridge model on Ansys platform

Cuntan Yangtze bridge including main section and approach bridge is located in Chongqing, China. The middle span is a suspension structure with 880.0 m. Ratio of rise to span in this bridge is 1/8.8 and the distance of two main cables is 39.2 m. The bridge elevation and the input point of turbulence wind are shown in Fig.14, and fluctuating wind simulation points are numbered. Height of fluctuating wind simulation points on main cable are given in Table 4. The north tower is 194.5 m and the south tower is 199.5 m in height. The main cable is made up of 127 high strength galvanized steel wires.

Fig. 14Cuntan Yangtze bridge’s configuration

Table 4Height of fluctuating wind simulation point on main cable

Number	(58, 30)	(57, 31)	(56, 32)	(55, 33)	(54, 34)	(53, 35)	(52, 36)	51
Height (m)	213.06	206.01	199.14	192.18	185.28	178.38	171.48	164.58
Number	(50, 38)	(49, 39)	(48, 40)	(47, 41)	(46, 42)	(45, 43)	44	37
Height (m)	161.36	158.1	154.77	151.46	148.16	144.86	141.58	164.58

A three-dimensional finite element model was set up on the ANSYS platform. Spatial beam4 element was used to simulate main girder and beam44 element was used to simulate main towers. Link10 element with three degrees of freedom was used to simulate main cables and suspenders. Pavement and railings’ stiffness contributions were neglected and lumped masses account for them were equal distributed to the main girder with mass21 element. Combin14 element was selected to simulate damper. According to the design, material properties and elements’ characteristic were added in the model and given in Table 5. Ernst equation of equivalent modulus of elasticity were used to calculate linearized stiffness of back cables’ nonlinearity stiffness. According to the bridge design, the deck and main towers were coupled in three degrees of freedom, including vertical displacement, transverse displacement, and rotation around longitudinal direction. Two main cables were fixed on the top of towers, and the bottoms of main cables were fixed at the bases. Two main towers were also fixed at the bases without considering the soil-pile structure interaction. The bridge was dispersed into 818 elements and 721 nodes.

Table 5Type of material

Number	Modulus of elasticity (Pa)	Poisson’s ratio	Density (N/m³)	Material	Application
1	2.10E+11	0.3	7850	Q345QD	Main girder
2	2.00E+11	0.3	8650	High-strength steel wire	Main cable, suspension cable
3	3.45E+10	0.2	2650	C50 RC	Main tower
4	1.00E+15	0	0	–	Rigid transverse beam

Analyses were performed using modal approach, solving the bridge dynamics equations of equilibrium in generalized coordinates through a state space transformation based on the first twenty modes. The vibration modes of Cuntan Yangtze bridge were shown in Fig. 15.

Fig. 15Vibration modes of Cuntan Yangtze bridge

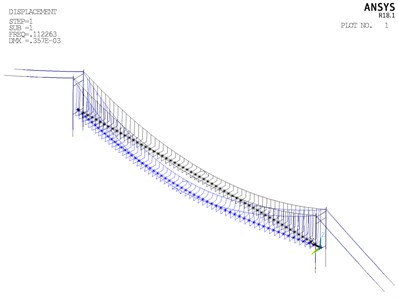
a) First vibration mode

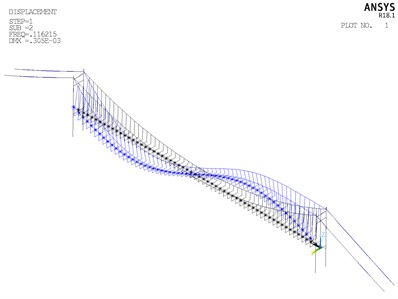
b) Second vibration mode

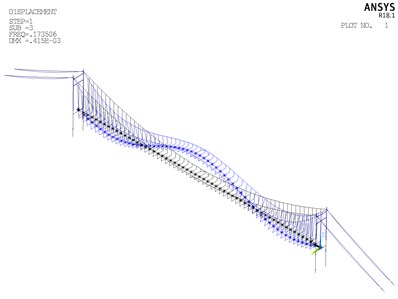
c) Third vibration mode

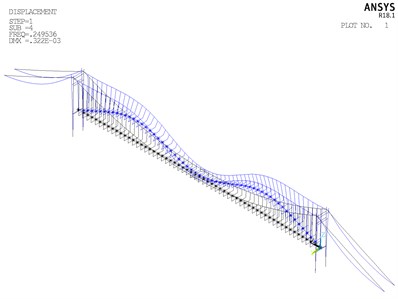
d) Fourth vibration mode

From Fig. 15, it can be summarized that the fundamental frequency is 0.1122 Hz, corresponding to the symmetric lateral bending vibration of girder, and the basic period of structure is short. The second frequency is 0.1162 Hz, corresponding to antisymmetric vertical bending vibration. This vibration mode of second frequency conforms to basic rule of the dynamic performance of the flexible structure. In the first twenty order vibration mode, vibrations of main cable and girder are taken as the principal vibration modes, without vibrations of main tower appearing. It is probably due to that stiffness of main tower is considerably larger than stiffness of main cable and girder. The distribution range of first twenty modal frequency is 0.1122 Hz to 0.4702 Hz, and distribution of overall frequency is relatively wide.

5. Analysis of buffeting performance

5.1. Vibration of main girder

The buffeting performance of long-span bridge was calculated at 0° wind attack angle, 28.1 m/s wind speed, with consistent mass matrix and Rayleigh damping. The damping ratio was 0.005 and the time step was 0.125 s. The computation time was 600.0 s. The resistance lift force and pitching moment aerodynamic admittance and the aerodynamic admittance coefficient derivative were taken as 1.0, Sears function and fitting function. RMS values in vertical, transverse and torsional direction of main girder were given in Fig. 16 with different aerodynamic admittance.

From Fig. 16, the following conclusions can be summarized: (1) RMS buffeting performances of main girder in three directions were basically symmetric centering the mid-span node. From 1/4 to 3/4 span, buffeting performance in three directions varied moderately. For sections near the span-ends, buffeting performance in three directions varied steeply. (2) Both lateral displacement and torsional displacement extreme value turned up at the mid-span. Extreme value in vertical displacement turned up at the 1/4 and 3/4 span. (3) In general, the buffeting performance of long-span bridge with Sears function, fitting function and 1.0 were well correlated. It was attributable to the accuracy of the bridge model. RMS buffeting performance of main girder with three different functions showed that the influence of aerodynamic admittance was remarkable. (4) The buﬀeting displacements from Sear function was close to that when the aerodynamic admittance function was taken as the fitting function. When the aerodynamic function taken as 1.0, the buﬀeting displacements were totally larger than the other two cases. Hence, if there is no available measured aerodynamic admittance function, the function is suggested to be taken as Sear function. If conservative design is indeed needed, the function is suggested to be taken as 1.0 for the safety.

Fig. 16RMS buffeting performance of main girder

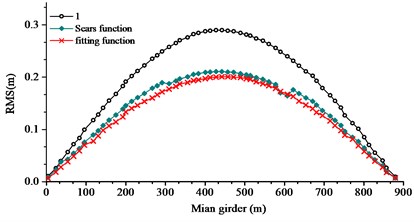
a) Lateral displacement

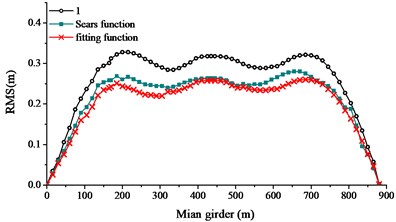
b) Vertical displacement

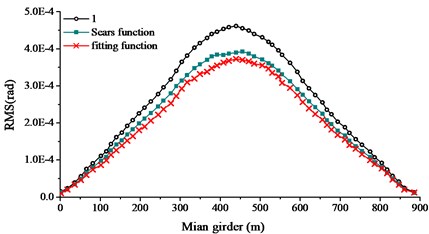
c) Torsional displacement

5.2. Vibration at different wind speeds

In order to search the relationship of wind speed and aerodynamic admittance influence, buffeting performance of long-span bridge at different wind speeds were collected. The wind speed changed from 20.0 m/s to 60.0 m/s, with an interval of 5.0 m/s. Sears function, 1.0 and fitting function were used to calculate the buffeting performance with the same turbulent wind. Comparison of RMS, internal force and bending moment were given in Figs. 17-19.

From Figs. 17-19, the following conclusions can be summarized: (1) In the calculation range of wind speed, buffeting performance of long-span bridge kept the same trend, in all three directions. The vibration in vertical direction was largest, the vibration in lateral direction was second, and the vibration in torsional direction was smallest. (2) When the aerodynamic admittance was taken as 1.0, buffeting performance of long-span bridge was most obvious. When the aerodynamic admittance was taken as the fitting function, buffeting performance was relatively unapparent. (3) With the increasing of wind speed, aerodynamic admittance influence on buffeting performance become obviously. When the aerodynamic admittance was taken as 1.0, the buffeting performance was overestimated. Buffeting performance in vertical direction was most overestimated. (4) The deviation of three kinds of aerodynamic admittance was smallest in lateral direction, and the deviation was largest in vertical direction. This phenomenon was more evident in reduced natural frequency. (5) The fitting function was closer to the buffeting performance of bridge. The buffeting performance can be overestimate when the aerodynamic admittance was taken as 1.0.

Fig. 17Comparison of RMS with the different aerodynamic admittance

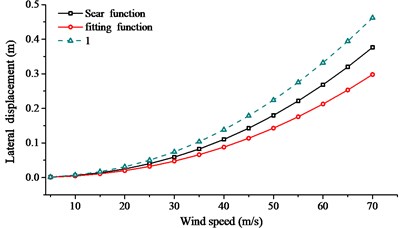
a) Lateral displacement

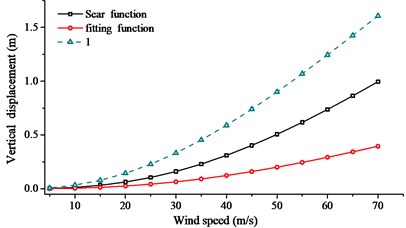
b) Vertical displacement

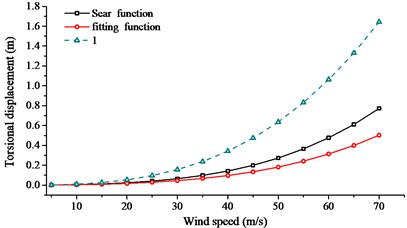
c) Torsional displacement

Fig. 18Comparison of internal force with different aerodynamic admittance

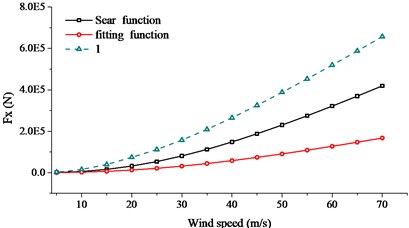
a) $F_{x}$ mean square

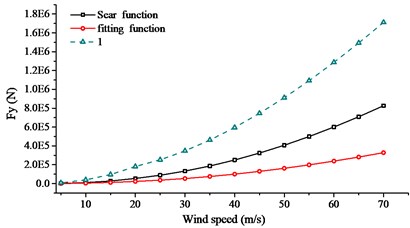
b) $F_{y}$ mean square

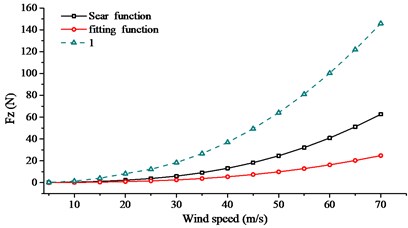
c) $F_{z}$ mean square

Fig. 19Comparison of internal force with different aerodynamic admittance

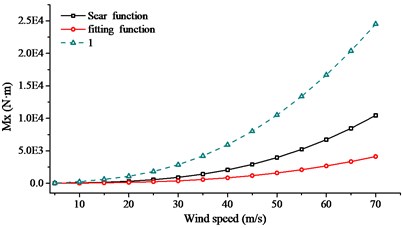
a) $M_{x}$ mean square

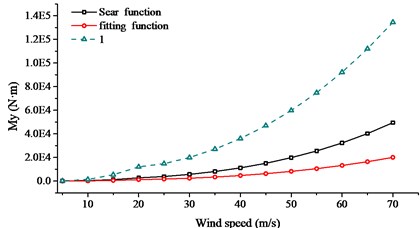
b) $M_{y}$ mean square

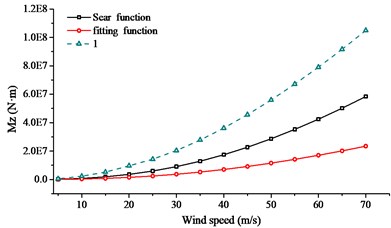
c) $M_{z}$ mean square

6. Conclusions

These conclusions are particularly relevant to long-span suspension bridges with relatively streamlined deck cross-sections on buffeting performance in the natural wind.

1) The aerodynamic admittance function identification result for a bridge deck is closely related to wind attack angle. Nevertheless, there is no distinct relationship between admittance function and wind attack angle under the conditions of wind tunnel test in this paper. The aerodynamic admittance function identification results have a small difference in the different wind speed working conditions.

2) Lift admittance was the largest in the aerodynamic admittance. Draft admittance increased obviously with the increasing of wind attack angle, and the trend of change was evident. Lift and moment admittance decreased with the increasing of wind attack angle, and the trend of change was slighter than draft admittance. More investigation utilizing the actively simulated flow characteristics are expected.

3) The influence of aerodynamic admittance on buffeting performance of bridge is affected by the wind speed significantly. The influence increases rapidly with the increasing of wind speed. And this appearance is most obvious in vertical displacement, otherwise in lateral displacement.

4) Under given conditions, adopting the Sears function as the admittance function of a similar streamlined box girder is reasonable, while the buffeting performance result obtained by adopting an admittance function as 1.0 is very conservative.

References

Etienne C., Jasna B. J., Jónas S. Buffeting response of a suspension bridge in complex terrain. Engineering Structures, Vol. 128, 2016, p. 474-487.

Publisher
Hu L., Xu Y. L. Extreme value of typhoon-induced non-stationary buffeting response of long-span bridges. Probabilistic Engineering Mechanics, Vol. 36, 2014, p. 19-27.

Publisher
Fenerci A., Øiseth O. Measured buffeting response of a long-span suspension bridge compared with numerical predictions based on design wind spectra. Journal of Structural Engineering, Vol. 143, 2017, p. 4017131.

Publisher
Mao J. X., Wang H., Tao T. Y., et al. Effects of the turbulent spatial correlation coefficient on buffeting responses of a triple-tower suspension bridge. Journal of Vibration and Shock, Vol. 35, Issue 10, 2016, p. 202-206.

Search CrossRef
Huang M. H., Lin Y. Y., Weng M. X. Flutter and buffeting analysis of bridges subjected to skew wind. Journal of Applied Science and Engineering, Vol. 15, Issue 4, 2012, p. 401-413.

Search CrossRef
Guo Z. W., Ge Y. J., Zhao L., et al. Linear regression analysis of buffeting response under skew wind. Wind and Structures, Vol. 16, Issue 3, 2013, p. 279-300.

Publisher
Wang H., Asce A. M., Li A. Q., et al. Comparison of ambient vibration response of the Runyang suspension bridge under skew winds with time-domain numerical predictions. Journal of Bridge Engineering, Vol. 16, 2011, p. 513-526.

Publisher
Wang H., Hu R. M., Xie J., et al. Comparative study on buffeting performance of Sutong bridge based on design and measured spectrum. Journal of Bridge Engineering, Vol. 18, Issue 7, 2013, p. 587-600.

Publisher
Hu L., Xu Y. L., Huang W. F. Typhoon-induced non-stationary buffeting response of long-span bridges in complex terrain. Engineering Structures, Vol. 57, 2013, p. 406-415.

Publisher
Zhang Z. T., Xie X. H. Wind-induced stochastic buffeting responses of bridges based on a varying frequency-increment sweeping method. Engineering Mechanics, Vol. 31, Issue 8, 2014, p. 101-107.

Search CrossRef
Debasis K., Samit R. C., Masanobu S. Conditional simulation of non-Gaussian wind velocity profiles: Application to buffeting response of Vincent Thomas suspension bridge. Probabilistic Engineering Mechanics, Vol. 29, 2012, p. 167-175.

Publisher
Wang H., Tao T. Y., Cheng H. Y., et al. A simulation study on the optimal control of buffeting displacement for the Sutong Bridge with multiple tuned mass dampers. Journal of Zhejiang University: Science A, Vol. 15, Issue 10, 2014, p. 798-812.

Publisher
Wen Y. K., Lu W. L. Parametric optimization and analysis of distributed TMD for buffeting response control of cable-stayed bridges. China Civil Engineering Journal, Vol. 47, Issue 6, 2014, p. 88-96.

Search CrossRef
Domaneschi M., Martinelli L., Po E. Control of wind buffeting vibrations in a suspension bridge by TMD: Hybridization and robustness issues. Computers and Structures, Vol. 155, 2015, p. 3-17.

Publisher
Nariman N. A. Control efficiency optimization and Sobol’s sensitivity indices of MTMDs design parameters for buffeting and flutter vibrations in a cable stayed bridge. Frontiers of Structural and Civil Engineering, Vol. 11, Issue 1, 2017, p. 66-89.

Publisher
Phan D. H., Kobayshi H. An experimental study of flutter and buffeting control of suspension bridge by mechanically driven flaps. Wind and Structures, An International Journal, Vol. 14, Issue 2, 2011, p. 153-165.

Publisher
Phan D. H., Nguyen N. T. Flutter and buffeting control of long-span suspension bridge by passive flaps: Experiment and numerical simulation. International Journal of Aeronautical and Space Sciences, Vol. 14, Issue 1, 2013, p. 46-57.

Publisher
Phan D. H., Kobayshi H. Analytical and experimental study on aerodynamic control of flutter and buffeting of bridge deck by using mechanically driven flaps. Structural Engineering and Mechanics, Vol. 46, Issue 4, 2013, p. 549-569.

Publisher
Tao T. Y., Wang H., Li A. Q. Influence of mid-tower on buffeting performance of a long-span triple-tower suspension bridge with continuous span. Journal of Vibration, Measurement and Diagnosis, Vol. 36, Issue 1, 2016, p. 131-137.

Search CrossRef
Li Y. L., Wang D. X., Wu C. P. Aerostatic and buffeting response characteristics of catwalk in a long-span suspension bridge. Wind and Structures, An International Journal, Vol. 19, Issue 6, 2014, p. 665-686.

Publisher
Wang H., Li A. Q., Zhao G. W., et al. Non-linear buffeting response analysis of long-span suspension bridges with central buckle. Earthquake Engineering and Engineering Vibration, Vol. 9, Issue 2, 2010, p. 259-270.

Publisher
Zhou Q., Zhu L. D., Zhao C. L. Numerical analysis on stochastic buffeting of cable-stayed bridge with slotted deck. China Civil Engineering Journal, Vol. 47, Issue 8, 2014, p. 98-106.

Search CrossRef
Wang H., Xu Z. D., Tao T. Y., et al. Field measurement study on the EPSD of non-stationary buffeting response of Sutong bridge based on WT. Engineering Mechanics, Vol. 33, Issue 9, 2016, p. 164-170.

Search CrossRef
Kim B. C., Yhim S. S. Buffeting analysis of a cable-stayed bridge using three-dimensional computational fluid dynamics. Journal of Bridge Engineering, Vol. 19, Issue 11, 2014, p. 04014044.

Publisher
Ibrahim K., Morgenthal G. Pseudo three-dimensional simulation of buffeting response under turbulent wind. Engineering for Progress, Nature and People, 2014, p. 309-316.

Publisher
Tubino F. Relationships among aerodynamic admittance functions, flutter derivatives and static coefficients for long-span bridges. Journal of Wind Engineering and Industrial Aerodynamics, Vol. 93, 2005, p. 929-950.

Publisher
Costa C. Aerodynamic admittance functions and buffeting forces for bridges via indicial functions. Journal of Fluids and Structures, Vol. 23, 2007, p. 413-428.

Publisher
Massaro M., Graham J. M. R. The effect of three-dimensionality on the aerodynamic admittance of thin sections in free stream turbulence. Journal of Fluids and Structures, Vol. 57, 2015, p. 81-90.

Publisher
Hejlesen M. M., Rasmussen J. T., Larsen A., et al. On estimating the aerodynamic admittance of bridge sections by a mesh-free vortex method. Journal of Wind Engineering and Industrial Aerodynamics, Vol. 146, 2015, p. 117-127.

Publisher
Zhao L., Ge Y. J. Cross-spectral recognition method of bridge deck aerodynamic admittance function. Earthquake Engineering and Engineering Vibration, Vol. 14, 2015, p. 595-609.

Publisher
Hua X. G., Ni Y. Q., Chen Z. Q., et al. An improved perturbation method for stochastic finite element model updating. International Journal for Numerical Methods in Engineering, Vol. 73, 2008, p. 1845-1864.

Publisher

Cited by

Study on the Influence of Wind Fairing Parameters on the Aerodynamic Performance of Long-Span Double-Deck Steel Truss Suspension Bridge

(2024)

Study on the influence of the fully enclosed barrier on the vortex-induced vibration performance of a long-span highway–railway double-deck truss bridge

(2024)

Investigation of Vortex-Induced Vibration of Double-Deck Truss Girder with Aerodynamic Mitigation Measures

(2023)

A Numerical-Experimental Framework to Separate the Effects of Different Turbulence Components on the Buffeting Forces of Bluff-body Structures

Bo Wu | Jianting Zhou | Jingzhou Xin | Hong Zhang | Fengbo Wu

(2023)

Research on Mechanism of Vortex-Induced Vibration Railing Effect of Double-Deck Large-Span Suspension Bridge

(2023)

Measurements of the unsteady lift force on a 5:1 rectangular cylinder based on active-passive hybrid wind tunnel tests

Shaopeng Li | Xin Li | Jingyang Li | Yi Su | Bo Wu

(2023)

Investigation of the aerodynamic characteristics of single-box girders with different aspect ratios

Zhisheng Xue | Xiaowei Wang | Juncheng Zhou | Zhao Xiao | Xin Deng

(2023)

Combining active and passive wind tunnel tests to determine the aerodynamic admittances of a bridge girder

(2022)

Safety Prediction Using Vehicle Safety Evaluation Model Passing on Long‐Span Bridge with Fully Connected Neural Network

(2019)

About this article

Received

28 January 2018

Accepted

05 August 2018

Published

15 February 2019

SUBJECTS

Flow induced structural vibrations

DOI

https://doi.org/10.21595/jve.2018.19681

Keywords

aerodynamic admittance

buffeting performance

wind tunnel test

long-span bridge

Acknowledgements

This study is financially supported by the National Natural Science Foundation of China (51578098 and 51608074), Fundamental Research Funds for the Central Universities (106112017CDJXY200009, 106112016CDJRC000101), Graduate Scientific Research and Innovation Foundation of Chongqing (CYB17042).

Author Contributions

Yao Gang contributed to the conception of the study. Yang Yang contributed significantly to analysis and manuscript preparation and wrote the manuscript. Wu Bo performed the data analyses. Liu Lianjie helped perform the wind tunnel test. Zhang Liangliang helped perform the analysis with constructive discussions.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2023 11 27

Investigation of the aerodynamic characteristics of single-box girders with different aspect ratios

Zhisheng Xue, Xiaowei Wang, Juncheng Zhou, Zhao Xiao, Xin Deng

Research article

2021 08 11

Flutter performance optimization of a long-span truss girder bridge in mountainous canyon

Muhammad Roshan Yousaf, Yongfu Lei, Mingshui Li

Research article

2019 10 19

Effects of the wide-body suspension bridge auxiliary structure on flutter characteristics by CFD

Zhijun Ni, Cong Zhang, Liangliang Zhang, Lianjie Liu

Research article

2017 05 15

Numerical computation for vibration characteristics of long-span bridges with considering vehicle-wind coupling excitations based on finite element and neural network models

Ling-bo Wang, Pei-wen Jiang

Y. Gang, Y. Yang, W. Bo, L. Lianjie, and Z. Liangliang, “Aerodynamic admittance influence on buffeting performance of suspension bridge with streamlined deck,” Journal of Vibroengineering, Vol. 21, No. 1, pp. 198–214, Feb. 2019, https://doi.org/10.21595/jve.2018.19681

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/jve.2018.19681
UR  - https://doi.org/10.21595/jve.2018.19681
TI  - Aerodynamic admittance influence on buffeting performance of suspension bridge with streamlined deck
T2  - Journal of Vibroengineering
AU  - Yang, Yang
AU  - Gang, Yao
AU  - Bo, Wu
AU  - Lianjie, Liu
AU  - Liangliang, Zhang
PY  - 2019
DA  - 2019/02/15
PB  - JVE International Ltd.
SP  - 198-214
IS  - 1
VL  - 21
SN  - 1392-8716
SN  - 2538-8460
ER  - 

Copy Ris

Copied to clipboard!

@article{Yang_2019,
	doi = {10.21595/jve.2018.19681},
	url = {https://doi.org/10.21595/jve.2018.19681},
	year = 2019,
	month = {feb},
	publisher = {{JVE} International Ltd.},
	volume = {21},
	number = {1},
	pages = {198--214},
	author = {Yang Yang and Yao Gang and Wu Bo and Liu Lianjie and Zhang Liangliang},
	title = {Aerodynamic admittance influence on buffeting performance of suspension bridge with streamlined deck},
	journal = {Journal of Vibroengineering}
}

Copy Bibtex

Copied to clipboard!

[1]Y. Yang, Y. Gang, W. Bo, L. Lianjie, and Z. Liangliang, “Aerodynamic admittance influence on buffeting performance of suspension bridge with streamlined deck,” Journal of Vibroengineering, vol. 21, no. 1, pp. 198–214, Feb. 2019, doi: 10.21595/jve.2018.19681.

Copy IEEE

Copied to clipboard!

Yang, Yang, Yao Gang, Wu Bo, Liu Lianjie, and Zhang Liangliang. “Aerodynamic Admittance Influence on Buffeting Performance of Suspension Bridge with Streamlined Deck.” Journal of Vibroengineering 21, no. 1 (February 15, 2019): 198–214. https://doi.org/10.21595/jve.2018.19681.

Copy Chicago

Copied to clipboard!

Aerodynamic admittance influence on buffeting performance of suspension bridge with streamlined deck

Abstract

1. Introduction

2. Description of wind tunnel test

2.1. Description of subsection elastic model

2.2. Description of subsection rigid model

2.3. Description of wind tunnel

2.4. Results of aerostatic coefficients

2.5. Results of aerodynamic admittance

3. Sectional forces in time domain

4. Bridge model on Ansys platform

5. Analysis of buffeting performance

5.1. Vibration of main girder

5.2. Vibration at different wind speeds

6. Conclusions

References

Cited by

About this article

Related Articles