Fault diagnosis of gearbox based on the nonlinear output frequency response functions and PNN

1. Introduction

Gearbox plays an important part in modern industry and the its advantage makes it widely used in automobile, airplane, wind power system [1] etc. In general, the inside of the gearbox is made up of bearings, shafts and gears. Different from simple components, the failure and failure modes are various. Thus, the importance of fault diagnosis for gearbox is obviously.

In general, the frequency domain fault detection approaches are preferred in practice [2]. However, most of the frequency domain methods are conducted based on the linear theory, where the nonlinearities of the system are ignored or linearized.

Recently, a new concept known as the Nonlinear Output Frequency Response Functions (NOFRFs) has been proposed based on the Volterra series representation of a general class of nonlinear systems [3], which is expecting to solve these issues in the fault detection and fault diagnosis of nonlinear rotor-bearing systems. The NOFRFs is the natural extension of the Frequency Response Function (FRF) of linear systems, making it possible to analyze the nonlinear systems in the frequency domain in a similar way to linear systems. The NOFRFs based fault detection and fault diagnosis of nonlinear systems has also been widely studied, i.e. Cao et al. [4] combined the NOFRFs of the nonlinear system and the evidence theory for the fault detection and diagnosis of nonlinear complex systems. Peng et al. [5] used the NOFRFs to detect cracks in beams, showing that the NOFRFs are a sensitive indicator of the presence of cracks under an appropriate input excitation. In Zhao et al. [6], the nonlinear transmissibility derived by the NOFRFs were applied in the condition monitoring of structure damages.

In this study, the NOFRFs concept is applied in the feature extraction of nonlinear gearbox systems, and the results indicate that the higher order NOFRFs are more sensitive than the output frequency response to nonlinear faults which can be used to detect and quantify the nonlinear faults of the system. Then, the PNN is mentioned to classify the failure modes. These two methods work together to complete the fault diagnosis of the gearbox.

2. The NOFRFs based analysis of nonlinear systems

2.2. The NOFRFs of nonlinear systems

The NOFRFs of the nonlinear system is defined as:

4

$G_n\left(j\omega \right)=\frac{Y_n\left(j\omega \right)}{U_n\left(j\omega \right)},n=1,\dots ,N,$

where $Y_n\left(\mathrm{j}\omega \right)$ is the $n$th order output spectrum of the system, and:

5

$U_n\left(j\omega \right)=\frac{1/n^{1/2}}{{\left(2\pi \right)}^{n-1}}{\int }_{{\omega }_1+\cdots +{\omega }_n=\omega }\prod _{i=1}^{n}U\left(j{\omega }_i\right)d{\sigma }_{\omega }=FFT\left[u^n\left(t\right)\right].$

Is the $n$th input, such that the output spectrum Eq. (2) can be rewritten as:

6

$Y\left(j\omega \right)={\sum }_{n=1}^N{Y}_n\left(j\omega \right)={\sum }_{n=1}^N{G}_n\left(j\omega \right)U_n\left(j\omega \right).$

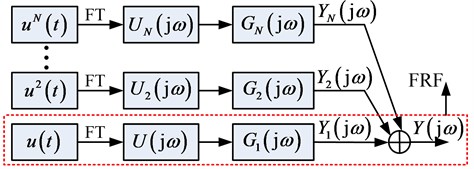
The new representation Eq. (6) indicate that the nonlinear system which can be represented by a Volterra series can be analyzed, similar to the FRF method of linear systems, by suing the NOFRFs. The approach is illustrated in Fig. 1.

It is worth noticing that, when the input of the nonlinear system is harmonic as:

7

$u\left(t\right)=A\mathrm{c}\mathrm{o}\mathrm{s}\left({\omega }_{F}t+\beta \right),$

where $A$ is the magnitude of the input signal, ${\omega }_F$ and $\beta$ are the input frequency and the phase, respectively, the NOFRFs based representation of the system can be written as:

8

$Y\left(j{\omega }_F\right)=G_1\left(j{\omega }_F\right)U\left(j{\omega }_F\right)+G_3\left(j{\omega }_F\right)U_3\left(j{\omega }_F\right)+G_5\left(j{\omega }_F\right)U_5\left(j{\omega }_F\right)+\cdots ,$
$Y\left(j2{\omega }_F\right)=G_2\left(j2{\omega }_F\right)U\left(j2{\omega }_F\right)+G_4\left(j2{\omega }_F\right)U_4\left(j2{\omega }_F\right)+G_6\left(j2{\omega }_F\right)U_6\left(j2{\omega }_F\right)+\cdots ,$
$⋮$

where the NOFRFs under a harmonic input is independent to the input magnitude $A$.

In practice, the NOFRFs of the nonlinear system can be estimated by using the LS, where the truncation order $N$ is assumed to be sufficient and a set of input with magnitudes are required. In this study, the NOFRFs under the harmonic input is applied for the feature extraction of the nonlinear gearbox system instead of the traditional frequency response detection method.

Fig. 1The NOFRFs based analysis of a nonlinear system

3. Fault classification based on PNN classifier

The PNN, first proposed by Dr. D. F. Speeht in 1989, is a branch of the radial basis Network, belonging to the feedforward Network. It has the following advantages: simple learning process, fast training speed; Classification is more accurate, fault tolerance and so on. In essence, it belongs to a supervised network classifier based on Bayesian minimum risk criteria.

Fig. 2Basic structure of PNN

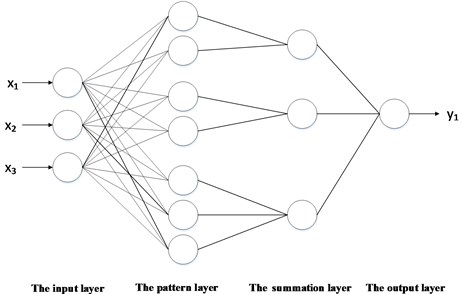
PNN generally have the following four layers: input layer, mode layer, summation layer, and output layer. In some materials, the pattern layer is also called the hidden layer, and the summation layer is called the competition layer. The input layer is responsible for transmitting the feature vector to the network, and the number of input layers is the number of sample features. The mode layer is connected to the input layer by a connection weight. Calculate the degree of matching between the input feature vector and each mode in the training set, that is, the similarity, and send the distance to the Gaussian function to obtain the output of the mode layer. The number of neurons in the pattern layer is the number of input sample vectors, that is, how many samples there are, and how many neurons there are. The summation layer is responsible for connecting the pattern layer units of each class. The number of neurons in this layer is the number of categories of samples. The output layer is responsible for outputting the highest score in the summation layer.

4. Case study

The data sets used in this paper come from the 2009 PHM Conference Data Analysis Competition.

5. Conclusions

The NOFRFs of nonlinear systems are the natural extension of the FRF for linear systems, which can be used for nonlinear systems analyses. In this study, the feature extraction of nonlinear gearbox system was completed by using NOFRFs concept, and then the fault mode was classified by using PNN classifier. The diagnostic results are obtained by study the vibration signals of gearbox. The results show that the way presented in this study can diagnose the gearbox failure perfectly.