Dynamic analysis of the moving mechanism of the reciprocating compressor with clearance joints

1. Introduction

Reciprocating compressors are widely used in the industrial field such as natural gas transportation and storage, petrochemical, chemical, and refrigeration industries, and have pivotal industrial states. The fault detecting and diagnosing technology for the reciprocating compressor has always been a hot topic for researches [1]. Especially for failures of the moving mechanism, which are core components in a reciprocating compressor, it may cause serious accidents, and is difficult to monitor and diagnose. Clearance faults on the joint are the most common faults in the moving mechanism a reciprocating compressor, due to wear and assembly error. In previous, scholars like Flores [2, 3] and Mohamed [4] have made a great deal of achievements in the joints with clearance for multi-body systems. Zhao [5] presented a parameters optimization method for joints clearance model and applied it to the simulation of the reciprocating compressor. Cheng [6] analyze the dynamic response of a reciprocating compressor with a revolute clearance joint. However, so far, there are no efficient methods for diagnosing these failures. The reason can be attributed to two aspects. For one hand, the reciprocating compressors, a symbol for reciprocating machines, have complicated structure, several various forms of motions and working load, poor working conditions, and abundant motivating source. As a result, that the faults have strongly non-linear and complex signals, and couldn’t be easily monitored and identified. On the other hand, the moving mechanism is inside the hermetic chamber, which causes that there are few effective approaches to extract the fault information [7]. Therefore, it is necessary to investigate the dynamic behaviors of the mechanism under faults for revealing the fault mechanism.

This paper aims at the clearance faults on the joints of the moving mechanism, investigating the dynamic behaviors of the moving mechanism under clearance fault and exploring the relationship between these behaviors and the clearance faults. We take the clearance size and the number of clearance into consideration and establish a dynamic model of the moving mechanism with clearance by the software ADAMS. Through dynamic analysis and non-linear analysis of the model, we try to find out the effect of the clearance faults on the dynamic behavior of the mechanism and to reveal the fault mechanism.

2. The model of the reciprocating compressor

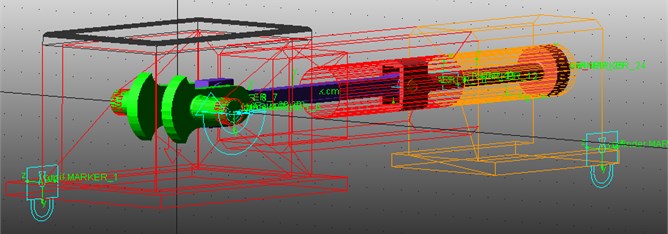
In this paper, a single-stage single-acting reciprocating compressor is taken as investigating object. We establish its simplified model with clearance joints in commercial software ADAMS, as shown in Fig. 1. The model is mainly composed of the body, crank, connecting rod, crosshead, piston assembly and cylinder. Table 1 provides the major characteristics of the model.

Fig. 1The schematic diagram of the reciprocating compressor

2.2. The clearance model

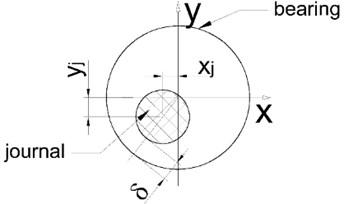
In previous working, the revolute joint with clearance model mainly includes the massless rod model, the two mode model and the three mode model [2, 6]. This paper employed the three mode model, describing the journal inside the bearing that has three modes: free flight mode, contact mode, and impact mode, as shown in Fig. 2.

The contact condition for the revolute joint with clearance can be given by Eq. (3):

3

$\delta =e-\sqrt{x_j^2+y_i^2},$

where $e$ is the radial clearance between journal and bearing, $x_j$ and $y_j$ are the relative displacements. $\delta <$ 0 corresponds to impact, $\delta =$ 0 represents contact, and $\delta >$ 0 means free flight.

Fig. 2The clearance revolute model

3. Dynamic simulation of the model

In order to investigate the relationship between the clearance fault and the dynamic behavior of the moving mechanism, we take different clearance sizes and different numbers of clearance into consideration, exploring the effect of these factors on the dynamic behaviors of moving part. During the simulation, we choose Gear Stiff integrator (GSTIFF) and integral formulation SI2; the speed of the crankshaft is 500 (rpm); the step time is 0.0001 (s); the integration tolerance is 1E-005.

3.2. Simulation for clearance fault on the joint between connecting rod and crosshead

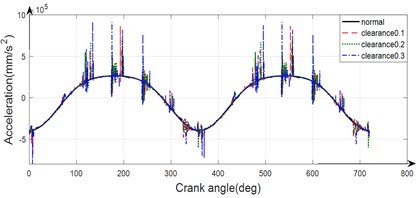
In this case, we set the revolute joint between the connecting rod and crosshead with clearance 0.1 mm, 0.2 mm, 0.3 mm, and set the other joints as ideal joints, investigating the effect of different size clearance joint between connecting rod and crosshead on the dynamic response of moving mechanism. Fig. 4 shows the dynamic response of the moving mechanism in the case of clearance fault on the joint between the connecting rod and crosshead.

Fig. 3The dynamic response of the moving mechanism in the case of clearance joint between crank and connecting rod

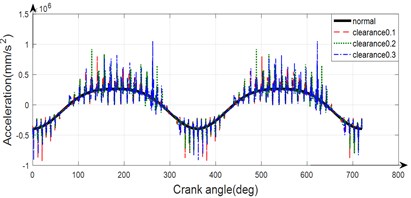
Fig. 4The dynamic response of the moving mechanism in the case of clearance joint between connecting rod and crosshead

3.3. Simulation for clearance fault on both joints of the connecting rod

In the case of clearance faults on both joints of the connecting rod, we set both the revolute joint between connecting rod and crank, and the joint between the connecting rod and crosshead with clearance 0.1 mm, 0.2 mm, 0.3 mm, and set the other joints as ideal joints, to study the dynamic response of the moving mechanism as the number of clearance joints increasing, so do the size of clearance. Fig. 5 shows the dynamic response of the moving mechanism in the case of clearance fault on the both joint of the connecting rod.

Fig. 5The dynamic response of the moving mechanism in the case of clearance joint between connecting rod and crosshead

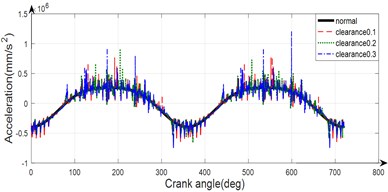
Fig. 6Comparison of the dynamic response of the mechanism in different case

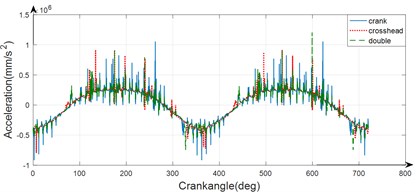
4. Result discussion and non-linear analysis

From Fig. 3-5, we can see that the clearance size strongly affect the acceleration of the mechanism. As the clearance size increase, the acceleration oscillates more intensely and has the higher amplitude.

Fig. 6 shows the comparison of the dynamic response of the mechanism in the above cases. As shown in Fig. 6, the clearance number also strongly influence the dynamic behaviors of the moving mechanism, and the acceleration in the double clearance fault case oscillates more intensely and has a higher amplitude than any of the other case. In addition to that, the position where the clearance faults happen also affects the dynamic behavior of the mechanism.

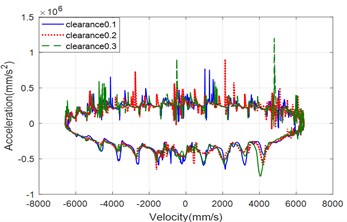
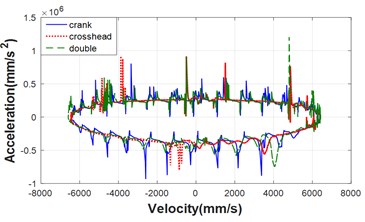
According to the above dynamic analysis for the moving mechanism with clearance, it is not difficult to draw the phase trajectories diagram and discuss the chaotic behavior of the mechanism. Fig. 7, 8 show the phase trajectories of velocity-acceleration diagram for the three cases. As can be seen from the two figure, as the clearance size increases, it is more possible to show the chaos behavior, and the number of the clearance also affects the chaotic behavior of the mechanism.

Fig. 7The phase trajectories of the velocity-acceleration with different clearance size in the three case: a) the case of clearance joint between crank and connecting rod, b) the case of clearance joint between connecting rod and crosshead, c) the case of clearance joint of both connecting

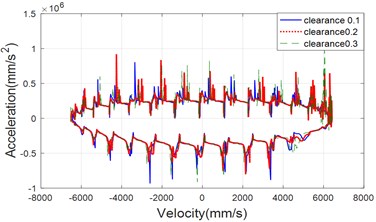
a)

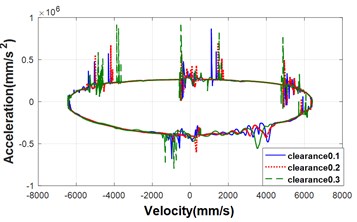
b)

c)

Fig. 8The comparison for phase trajectories of the velocity-acceleration in the different case with clearance 0.3

5. Conclusions

In order to investigate the effect of the clearance faults on the dynamic behavior of the moving mechanism in a reciprocating compressor, a dynamic model for the mechanism with clearance is established via software ADAMS in this paper. We take into the clearance size and clearance number into consideration and set clearance fault on the joint between the crank and connecting rod, the joint between connecting rod and crosshead and both joints of connecting rod. As the simulation result shown, we can conclude that the clearance size strongly influences the dynamic behaviors of the mechanism, the bigger size is, the more violent the acceleration oscillates, and the higher amplitude it has. We also get that the number of the clearance faults and the position the faults happened strongly affect the dynamic response of the mechanism. What’s more, as the clearance size increases, or the numbers of clearance faults increase, it is more possible to displays chaotic behavior.