A passive diffusion model of fluorescein derivatives in an in vitro human brain microvascular endothelial cell (HBMEC) monolayer

2.1. Cell culture

Penicillin-streptomycin solution (100x), MEM vitamin solution (100x), endothelial cell growth supplement (ECGS), fetal bovine serum (FBS), and NuSerum culture supplement were all obtained from Corning Life Sciences. Sodium pyruvate solution (100 mM), RPMI 1640 medium containing 2 mM L-glutamine were purchased from GE Healthcare Life Sciences. Non-essential amino acids were obtained from Gibco laboratories. Human brain microvascular endothelial cells (HBMEC) were isolated and purified as previously described [29]. Cells were cultured in RPMI 1640 medium with 10% fetal bovine serum, 10% NuSerum, 30 µg/ml ECGS, 15 U/ml of heparin, 11.0 mg/ml of sodium pyruvate, 100 U/ml of penicillin, 100 µg/ml of streptomycin, nonessential amino acids, and vitamins. HBMEC cultures were incubated at 37°C in a humid environment with 5% CO₂.

2.2. In vitro studies

Fluorescein isothiocyante isomer I (FITC), fluorescein free acid, and fluorescein sodium salt (NaFl) fluorescent tracers were all purchased through Sigma-Aldrich. The molecular weights for FITC, fluorescein, and NaFl were 389.38, 332.31, and 376.28 respectively. HBMEC were grown to confluence followed by washing the monolayer with hanks balanced salt solution (HBSS, Corning Life Sciences) and cell detachment with 0.05% trypsin containing EDTA (GE Healthcare Life Sciences). The suspended cells were seeded into Falcon^TM 48 well plates at a density of 7.0×10⁴ cells per well and grown to confluence in an incubator for 1-2 days.

Confluent cells were aspirated of media and replaced with 200 µl of 0.1 mg/ml fluorescent tracer solutions in basal RPMI 1640 medium. Wells were incubated in tracer solutions at 3, 6, 9, 12, 15, 18, 21, and 24 hours with a sample size of 6 wells per time point for all three tracers. All wells were washed twice with sterile phosphate buffered saline (1x) to remove excess fluorescent tracer and replaced with phenol free RPMI 1640 medium (Gibco Laboratories) at a volume of 200 µl. Fluorescent intensity of the wells were recorded using a SpectraMax M2^e (Molecular Devices, LLC) plate reader with excitation and emission settings of 492 and 518 nm respectively for FITC, 490 and 514 nm for fluorescein, and 460 and 515 nm for NaFl.

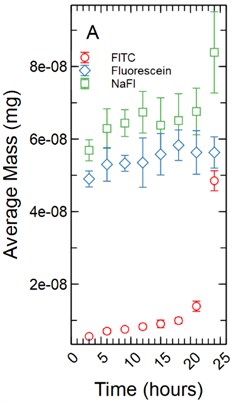
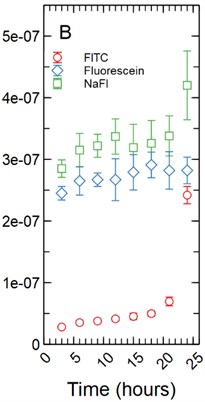
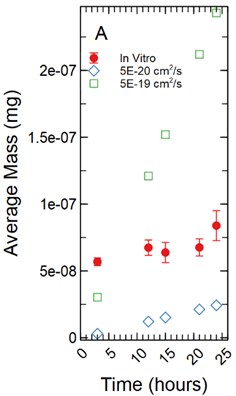
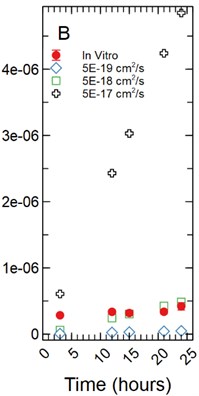
The fluorescent intensity was correlated to concentration (mg/ml) using a dilution curve generated for each fluorescent tracer dissolved in phenol red-free RPMI 1640 for various known concentrations. The fluorescent intensity of tracer found in the HBMEC monolayers were converted to concentration using the dilution curves. The total mass in mg for each monolayer was determined by multiplying the volume the monolayer occupied in each well by the calculated concentration. As cell monolayer thicknesses can vary based on cell type a 1 µm and 5 µm thickness were assumed. The 48 well plates have a growth area of 0.75 cm² and accounting for a 1 µm monolayer thickness results in a volume of 2.36E-04 ml being occupied by the monolayer while a 5 µm thickness results in a volume of 1.18E-03 ml being occupied by the monolayer. The total mass in mg was averaged and standard deviation calculated for each time point for each tracer (Fig. 1).

Fig. 1a) Total mass in mg averaged for each time point per fluorescent tracer for a 1 µm thickness; b) total mass in mg averaged for each time point per fluorescent tracer for a 5 µm thickness

a)

b)

2.3. Passive diffusion model

The in vitro system was composed of a cylindrical well where uptake of tracer could occur in the $x$, $y$, and $z$-directions (Fig. 2) with the HBMEC. Assuming the transport mechanism is primarily through passive diffusion, the following simplifications were made: (1) no reaction terms, (2) no binding, (3) movement of tracer was uniform in all directions, and (4) an overall diffusion constant is appropriate. These assumptions allow for the reduction of the problem from a three dimensional (3D) space to a one dimensional (1D) space where concentration could be determined in the $z$-direction. A 1D partial differential equation (PDE, Eq. (1)) was generated with one initial condition (Eq. (2)) and two boundary conditions (Eqs. (3-4)). Simulations were run in MATLAB 2015b.

Fig. 2a) In vitro cell culture of HBMEC where the monolayer thickness spans the z-direction; b) introduction of fluorescent tracers to the HBMEC for incubation. Uptake of the tracer is assumed to be uniform in all directions

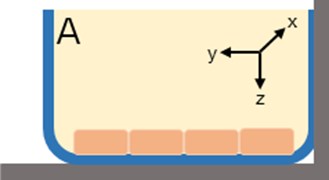
a)

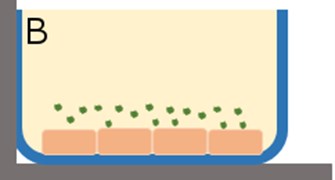
b)

The boundary concentration was set at 0.1 mg/ml for all simulations with the monolayer thickness varying between 1 and 5 µm which resulted in a monolayer volume of 2.36E-04 and 1.18E-03 ml respectively. A tracer concentration of 0.1 mg/ml was chosen for simulations to match the concentration used in the in vitro set-up. The monolayer thickness in the $z$-direction was divided into 70 evenly spaced pieces for simulations and the time span was restricted to 24 hours. A range of effective diffusion constants were simulated where the resulting concentration (mass/volume) was converted to mass in mg and the area under the curve for each time point was generated for comparison with the HBMEC in vitro data.

The in vitro data was split into a calibration and validation group where time points at hours 3, 12, 15, 21, and 24 were allocated to the calibration set and time points at hours 6, 9, and 18 were allocated to the validation set. A range of effective diffusion constants ($D_{eff}$, cm²/s) were selected for simulations and simulated time points at hours 3, 12, 15, 21, and 24 were extracted and compared to the in vitro time points at those hours to determine a range of diffusion constants that produced results not statistically significantly different from the in vitro data. The resulting diffusion constants were used to run simulations and extract time points at hours 6, 9, and 18 and those were compared to the in vitro time points at those hours. The percent error was calculated for the validation sets to determine how far the simulated models deviated from the in vitro model.

2.4. Statistical methods

The means of each experimental time point for each fluorescent tracer were compared using an Analysis of Variance (ANOVA) if equal variance could be assumed at all time points per tracer otherwise the non-parametric equivalent of an ANOVA (Welch Test) was used. Post-hoc comparisons were conducted if the $p$-value of the ANOVA was less than the alpha ($p<$0.05). The Games-Howell post-hoc test was used if the non-parametric ANOVA was conducted and a Tukey Honest Significant Differences (HSD) was used if the parametric ANOVA was conducted.

A linear regression comparison of slopes was used to compare the in vitro time points to the simulated time points for the calibration data at hours 3, 12, 15, 18, 21, and 24. A $p$-value less than 0.05 indicates the slopes of the in vitro and simulated models are significantly different while a $p$-value larger than 0.05 indicates the slopes are not statistically significantly different. All statistical testing was conducted using Minitab 18 software (Minitab, Inc).

3.1. In vitro diffusion of fluorescent tracers

With the assumption of a 1 µm monolayer thickness, the calculated total average mass (mg) of tracer for FITC ranged from 5.59E-09 mg with a standard deviation of 3.85E-10 mg after 3 hours of incubation to 4.85E-08 ± 2.76E-09 mg at 24 hours (Fig. 1(a)). A non-parametric Welch Test was used to compare average mass among all FITC time points at the 95% confidence level resulting in an $F$-statistic = 192.36 and a $p$-value of 0.00. A Games-Howell post-hoc multiple comparison test was used showing the 24 and 21 hour time points to be significantly greater than all earlier time points ($p$-value < 0.05). The 18 hour time point was significantly greater than the 3 through 12 hour time points ($p$-value < 0.05). The 15 hour time points were significantly greater than the 3 and 6 hour time points ($p$-value < 0.05). The 12, 9, and 6 hour time points were significantly greater than the 3 hour time point with $p$-values of 0.001, 0.00, and 0.022 respectively. Fluorescein range from 4.90E-08 ± 1.94E-09 mg at 3 hours to 5.63E-08 ± 4.31E-09 mg at 24 hours of incubation (Fig. 1(a)). An ANOVA was used to compare all time points among the fluorescein data set resulting in an $F$-statistic = 2.19 and a $p$-value = 0.056, no additional post-hoc statistical testing was conducted. NaFl range from 5.69E-08 ± 2.90E-09 mg at 3 hours to 8.39E-08 ± 1.12E-08 mg at 24 hours of incubation (Fig. 1(a)). A non-parametric Welch Test was conducted resulting in an $F$-statistic = 6.33 and a $p$-value = 0.001. A Games-Howell post-hoc test showed only the 24 hour time point being significantly greater than the 3 and 6 hour time points with $p$-values of 0.016 and 0.046 respectively. The 9 hour time point was significantly greater than the 3 hour time point with a $p$-value of 0.045.

Under the assumption of a 5 µm monolayer thickness, the calculated total average mass in mg of tracer for FITC ranged from 2.80E-08 mg with a standard deviation of 1.94E-10 mg after 3 hours of incubation to 2.42E-07 ± 1.40E-08 mg at 24 hours (Fig. 1(b)). Fluorescein range from 2.45E-07 ± 1.10E-08 mg at 3 hours to 2.82E-07 ± 2.16E-08 mg at 24 hours of incubation (Fig. 1(b)). NaFl range from 2.85E-07 ± 1.42E-08 mg at 3 hours to 4.20E-07 ± 5.58E-08 mg at 24 hours of incubation (Fig. 1(b)). The statistical testing at the 5 µm monolayer thickness returned the same results as those found above with the 1 µm monolayer thickness.

3.2. Linear Regression: FITC Calibration

For a 1 µm monolayer thickness, FITC calibration simulations run using effective diffusion constants ($D_{eff}$) of 5.00E-21, 1.00E-20, and 5.00E-20 cm²/s (Fig. 3(a)) created a range of data close to the in vitro calibration data set at hours 3, 12, 15, 18, 21, and 24 hours. The slopes of each simulated data set were statistically compared to the in vitro data set using a linear regression approach. There was not a significant difference in slopes comparing the 5.00E-21 cm²/s simulation to the in vitro data set with a $t$-statistic of 2.179 and a $p$-value of 0.066. The 1.00E-20 and 5.00E-20 cm²/s simulations yielded similar results with $t$-statistics of 2.011 and 0.314 respectively with $p$-values of 0.084 and 0.763 respectively.

With a 5 µm monolayer thickness, calibration simulations run using effective diffusion constants ($D_{eff}$) of 5.00E-21 and 1.00E-20 cm²/s (Fig. 3(b)) resulted in $t$-statistics of 1.647 and 4.865 respectively with $p$-values of 0.144 and 0.002 respectively when compared to in vitro data.

Fig. 3a) Simulations run under a 1 µm monolayer thickness assumption, all simulations were found to not be statistically significantly different from the in vitro data; b) simulations run under a 5 µm monolayer thickness assumption, using a simulated Deff of 5.00E-21 cm2/s was shown to not be statistically significant while a simulated Deff of 1.00E-20 cm2/s yielded a significant difference at a p-value of 0.002 for FITC

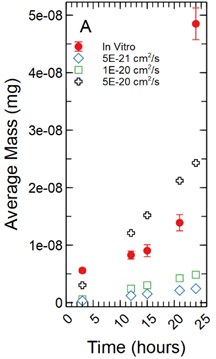
a)

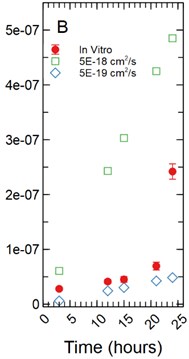
b)

3.3. Linear regression: fluorescein calibration

For a 1 µm monolayer thickness, fluorescein calibration simulations run using effective diffusion constants ($D_{eff}$) of 5.00E-21 and 1.00E-20 cm²/s (Fig. 4(a)) created a range of data close to the in vitro calibration data set at hours 3, 12, 15, 18, 21, and 24 hours. The slopes of each simulated data set were statistically compared to the in vitro data set using a linear regression approach. There was a significant difference in slopes comparing the 5.00E-21 and 1.00E-20 cm²/s simulations to the in vitro data set with $t$-statistic of 5.122 and 3.594 respectively and $p$-values of 0.001 and 0.009 respectively.

Fig. 4a) Simulations run under a 1 µm monolayer thickness assumption, all simulations were found to be statistically significantly different from the in vitro data with p-values < 0.05; b) simulations run under a 5 µm monolayer thickness assumption were found to be statistically significant (p-value < 0.05) for both the 1.00E-18 and 1.00E-17 cm2/s effective diffusion constants with the 5.00E-18 cm2/s diffusion constant gave a p-value of 0.547

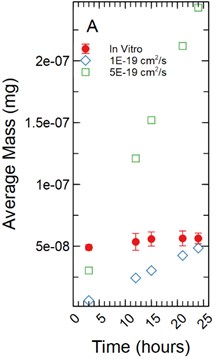
a)

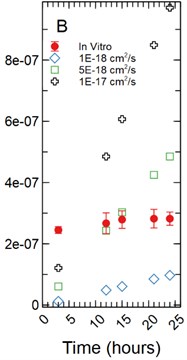
b)

With a 5 µm monolayer thickness, calibration simulations run using effective diffusion constants ($D_{eff}$) of 1.00E-18, 5.00E-18, and 1.00E-17 cm²/s (Fig. 4(b)) resulted in $t$-statistics of 31.364, 0.632, and 3.125 respectively and $p$-values of 8.65E-9, 0.547, and 0.017 respectively.

3.4. Linear regression: NaFl calibration

For a 1 µm monolayer thickness, fluorescein calibration simulations run using effective diffusion constants ($D_{eff}$) of 5.00E-20 and 5.00E-19 cm²/s (Fig. 5(a)) created a range of data close to the in vitro calibration data set at hours 3, 12, 15, 18, 21, and 24 hours. The slopes of each simulated data set were statistically compared to the in vitro data set using a linear regression approach. There was a significant difference in slopes comparing the 5.00E-20 and 5.00E-19 cm²/s simulations to the in vitro data set with $t$-statistic of 20.793 and 3.297 respectively and $p$-values of 1.49E-07 and 0.013 respectively.

With a 5 µm monolayer thickness, calibration simulations run using effective diffusion constants ($D_{eff}$) of 5.00E-19, 5.00E-18, and 5.00E-17 cm²/s (Fig. 5(b)) resulted in $t$-statistics of 20.131, 0.831, and 4.923 respectively and $p$-values of 1.87E-07, 0.433, and 0.002 respectively.

Fig. 5a) Simulations run under a 1 µm monolayer thickness assumption, all simulations were found to be statistically significantly different from the in vitro data with p-values < 0.05; b) simulations run under a 5 µm monolayer thickness assumption were found to be statistically significant (p-value < 0.05) for both the 5.00E-19 and 5.00E-17 cm2/s effective diffusion constants with the 5.00E-18 cm2/s diffusion constant gave a p-value of 0.547

a)

b)

3.5. Percent error: FITC, fluorescein, and NaFl validation

When increasing the effective diffusion ($D_{eff}$) constant of FITC, under a 1 µm assumption from 1E-20 to 5E-20 cm²/s shows a reduction in percent error of prediction of simulations (Table 1) at time points of 6 and 9 hours, but an increase in percent error of prediction at 18 hours of the validation data set using Eq. (5). When the monolayer thickness is increased to 5 µm and the $D_{eff}$ range is 5.00E-19 and 5E-18 cm²/s the percent error of prediction increased for all time points:

For fluorescein, under a 1 µm assumption, the $D_{eff}$ from 1E-19 to 5E-19 cm²/s shows a reduction in percent error of prediction of simulations (Table 2) at the 6 hour time point and an increase in error rate at the 9 and 18 hour time points (Table 2). Under a monolayer assumption of 5 µm there is a reduction in percent error at all three time points.

NaFl, under an assumed 1 µm monolayer thickness, produced a decrease in percent error at the 6 and 9 hour time points for $D_{eff}$ from 5E-20 to 5E-19 cm²/s and an increase in percent error at the 18 hour time point (Table 3). With a 5 µm monolayer thickness there is a decrease in all time points when the effective diffusion constant ($D_{eff}$) is increased from 5E-19 to 5E-18 cm²/s.