Experimental verification on applying indirect inverse substructuring analysis to identify coupling dynamic stiffness of mechanical assembly via planar surface

1. Introduction

In general, an electro-mechanical product consists of parts or components via mechanical assemblies. Quality inspection of an assembly considers tolerance and or size-coordination conventionally [1]. However, the dynamic quality of the involved assemblies should be also inspected in consideration of dynamic quality of a whole product [2]. Dynamic quality of a product is affected seriously by the dynamic quality of its mechanical assemblies. The dynamic quality of an assembly can be estimated via the dynamic characteristics of the coupling interface or joint connection(s) involved the assembly [3]. Identifying the joint-properties is complicated via conventional ‘positive’ methods [4, 5], which belong to dynamic substructuring analysis and result in low accuracy in engineering application.

Applying FRF-based inverse substructuring dynamic analysis is considered as the effective method determine the dynamic characteristics of joint or connection(s) of a mechanical assembly [6]. It has been applied to fix the eigenvalue of an assembly matrix [7]. In addition, due to the operational difficulty in testing the FRFs involved in the direct scheme of inverse substructuring analysis provided in literature [6], Lu Guangqing developed five indirect schemes of inverse analysis for identifying the coupling dynamic stiffness of a mechanical assembly [8] and vibrational structures [9]. The stiffness and eigenvalues can be used as two quantitative criterions of dynamic quality of a mechanical assembly. The theoretical completeness of the indirect schemes was validated analytically by simulations, and their feasibility and effectiveness in application in case of ideal coupling interface with point-to-point connection of mechanical assembly were also verified by experiments in literatures [8, 9].

This study applies the first and the second indirect schemes of inverse substructuring analysis of literature [8] to identify the stiffness of mechanical assembly with non-ideal coupling interface. An experimental model of the assembly via planar surface is designed, and the surface is equivalently discretized into a number of ‘point-to-point connections’ in order to meet the essential needs of the indirect schemes. Then, the FRFs involved are tested on the model, and the stiffnesses are computed by the schemes. The feasibility of applying the schemes is verified experimentally in case of the assembly via planar surface.

2. The indirect schemes to identify the coupling dynamic stiffness

In general, a mechanical assembly system with discrete couplings can be equivalently described by the model of two-level substructures with ‘substructure/component A-coupling connector-substructure/component B’, as shown in Fig. 1. The discrete couplings are denoted by $ca$ and $cb$, and the external input of exciting dynamic force on component B and the output response of dynamic displacement on component A are denoted by $ib$ and $oa$. The ‘FRF at system level’ of the assembly system is denoted by $H_s$, and the ‘FRF at component level’ of A and B are denoted by $H_A$ and $H_B$, respectively. The coupling dynamic stiffness of the connector is represented as $K_s$.

Fig. 1Model of two-level substructures with discrete couplings

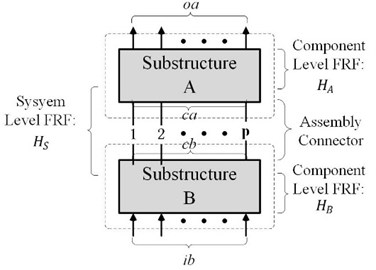
If choosing the same numbers of ($ia$, $ib$), ($oa$, $ob$) and ($ca$, $cb$), then five FRF-based indirect schemes of inverse substructuring analysis for determining coupling dynamic stiffness matrix, ${\mathit{K}}_s$, of connector can be derived [8]. Where, the first and second schemes are expressed as:

where, $\mathit{D}={\mathit{H}}_{caca}+{\mathit{H}}_{cbcb}$. Eqs. (1) and (2) show that testing the FRFs at system level on the coupling interfaces in assembling state is unnecessary. And using Eq. (1) and Eq. (2) to identify the stiffness need 5 and 6 FRF-matrices, respectively. For the first scheme, four FRFs at component level before assembly, ${\mathit{H}}_{oaca}$, ${\mathit{H}}_{cbib}$, ${\mathit{H}}_{caca}$ and ${\mathit{H}}_{cbcb}$, and one FRF at system level after assembly, ${\mathit{H}}_{s,oaib}$, are to be tested. For the second scheme, five FRFs at component level, ${\mathit{H}}_{caia}$, ${\mathit{H}}_{oaia}$, ${\mathit{H}}_{oaca}$, ${\mathit{H}}_{caca}$ and ${\mathit{H}}_{cbcb}$, and one FRF at system level, ${\mathit{H}}_{s,caia}$, are to be tested. All the FRFs are shown in Fig. 2.

3. Experimental model of mechanical assembly via planar surface

To verify the feasibility of applying both the first and the second indirect schemes to identify the coupling dynamic stiffness matrix, ${\mathit{K}}_s$, of mechanical assembly via planar surface, here designs an experimental model of the assembly with the connection of planar interface, as shown in Fig. 3. Components A and B consist of a steel plate (300×260×10 mm³) attached with four different mass of steel blocks by damping rubber cylinders ($\mathrm{\Phi }$35 mm), as shown in Fig. 3(a)-(c). They are assembled together via an ordinary hard rubber layer (3mm thick) as the planar connector, see Fig. 3(d). The discretized coupling points (No.1-8) and the positions of the blocks (No.1-4) are shown in Fig. 3(e).

Fig. 2The tested FRFs for the first and the second indirect schemes

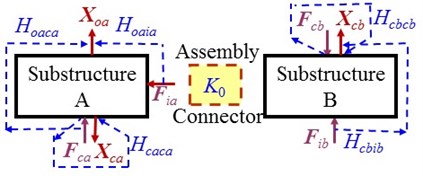
a) FRF at component level for the indirect schemes

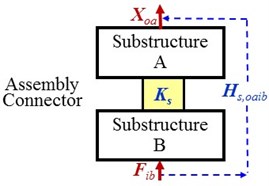
b) FRF at system level for the indirect schemes

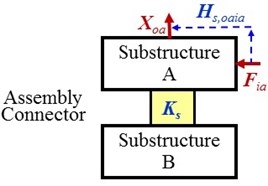
c) FRF at system level for the second indirect schemes

Fig. 3Experimental model of mechanical assembly with linear connection

a) Component A

b) Vertical view

c) Component B

d) Assembling system

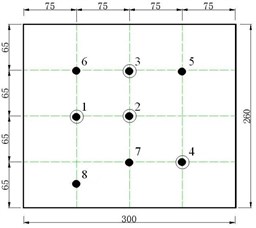
e) Discrete points

Because the FRFs involved in the indirect schemes of Eqs. (1) and (2) are required to be tested by “point-viro-excitation to point-displacement-response” on either the components A and B or their connection of planar surface, the surface should be discretized into a number of ‘point-to-point connections’, theoretically, there are infinite number of the discrete points. In order to check if it is valid to use limited discrete number of points instead of the infinite number of points equivalently, the planar surface is divided uniformly in grid, as shown in Fig. 3(e). Correspondingly, there are bi-, tri-, quad-, pent-, hexa-, hepta- and octa-coupled ‘point-to-point connections’ on the surface. By vibro-excitation tests, all the FRF-matrices of Eqs. (1) and (2) are acquired respectively in these seven cases of experimental models with discrete “point-to-point connections” under free state. The testing frequency is set to be 0-50 Hz in this study.

4. Experimental results

All the entries of the five and six square FRF-matrices involved in the first and second indirect schemes in the seven cases of “point-to-point connections” are tested firstly on the experimental model of mechanical assembly via planar surface, as shown in Fig. 3, the coupling dynamic stiffness matrix ${\mathit{K}}_s$ in each case is computed by Eq.(1) and Eq.(2) for the first and second scheme, respectively. The mean module spectra, $\left|K_s\left(f\right)\right|$, of diagonal entries of the matrix, $K_{sii}$ ($i=$ 1, 2, …, $p$, and $p=$ 2-8 is the number of discrete points), in the six cases are plotted in Fig. 4. Fig. 5 shows their amplified plots in range of 20-30 Hz.

Fig. 4Mean Ksf in testing frequency range in six cases of discrete points

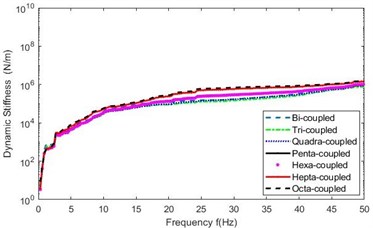
a) First indirect scheme

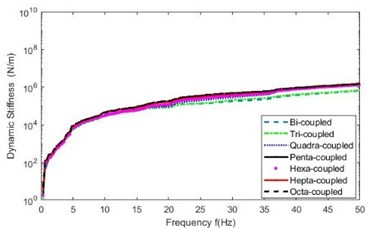
b) Second indirect scheme

Fig. 5Amplified mean Ksf in 20-30 Hz in the seven cases of discrete points

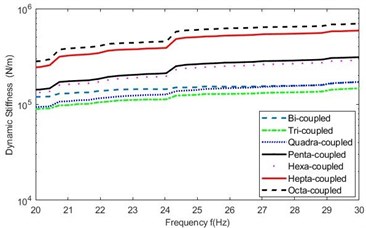
a) First indirect scheme

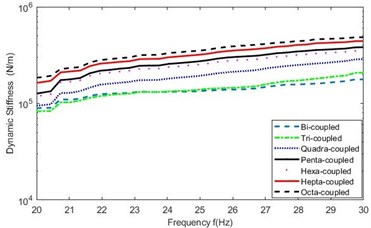
b) Second indirect scheme

To show the differences of the identified stiffnesses, here takes the mean $\left|K_s\left(f\right)\right|$ in case of octa-coupled connection as a reference, denoted by $\left|K_m\left(f\right)\right|$. The relative errors, $E_{mi}\text{,}$ ($i=$ 1, 2, …, 6) of the first six cases in full testing frequency range (0-50 Hz) are computed by:

where $N=$ 400 is the number of discrete frequencies. The computed $E_{mi}$ are listed in Table 1.

It can be seen from Figs. 3, 4 and Table 1 that:

(1) The identified stiffnesses in the seven cases of discrete point numbers are on the same order of magnitude, which is around 10⁴-10⁶ N/m and on practical order of hard rubber stiffness, as shown in Fig. 3. This verifies that discretizing the coupling interface of planar surface into “point-to-point connections” equivalently and applying the indirect scheme to identify the stiffness of mechanical assembly is feasible.

(2) Fig. 4 shows that the identified stiffness draws close to be stable with increase of the number of discretized points.

(3) Table 1 shows that, for the experimental model in this study, discretizing its planar surface into equivalent “point-to-point connections” results in closer mean values of identified stiffness, subsequently, smaller relative errors to the maximum number of discrete points (in case of octa-coupled connection). This is also demonstrated in Fig. 5. Implicitly, there probably exists an maximum number of discrete points for a specific mechanical assembly that can be approximately considered as the optimum number for discretizing the planar surface of assembly, instead of infinite number of discrete points.

(4) The second indirect scheme shows better performance than the first indirect scheme on discretizing the planar surface of a mechanical assembly, due to closer results of identified stiffness with increase of discrete points.

5. Conclusions

This study applies both the first and the second indirect schemes of inverse substructuring analysis to identify the coupling dynamic stiffness of mechanical assembly via planar surface, an experimental model is designed, and the surface is equivalently discretized into “point-to-point connections” in seven cases at first. Then, the stiffness is computed by the schemes using the FRF-matrices tested by vibro-excitation. As the results of the experimental study, the schemes are firstly verified to be feasible in engineering application to the assembly via planar surface as a connector. With increase of the number of discretized points, the identified stiffness approaches to a stable value. It seems that the second indirect scheme has better performance on discretizing the surface. This means implicitly that there probably exist definite discrete points of the surface for specific assembly to apply equivalently the schemes, instead of infinite number of discrete points.