Abstract
When identifying the sound sources with microphone array, sometimes the side-lobe effect is significant, increasing the amount of the microphones and enlarging the size of the microphone array will improve the identification performance. But it will increase the cost and complexity of the measurement system. In this paper, we proposed two kinds of methods to identify the sound source and suppress the sidelobe effect without increasing the microphones or enlarging the array size. We extended the wave superposition method to the measurement of the stable sound sources and applied this method to suppress the sidelobe effect successfully. The results of the simulations and experiments have proven that both the two methods can provide better identification results and reduce the side lobe significantly, suggesting our methods’ great potential in noise identification work.
1. Introduction
Recent years with the development of technology in acoustic field, amount of attention has payed on the method of sound field visualization for stable and moving vehicles, and the measurement method for sound source localization and sound field propagation mechanism [1].
2. Dynamic wave super position method based on holography
Koopmann [2-4] etc. proposed a wave superposition approach, the method can directly determining the distribution of the sound source inside the source strength which can be equivalent the source of the sound field, then to calculate the entire space, the method is to avoid the presence of the boundary element method and characteristics of singular integrals wave number of non-unique process also can solve the false sound source and side lobe other issues, but the method can only be used for static source of the sound field. For stationary sound source can be directly used by the following formula was accepted point of wave superposition approach the sound pressure, as shown in Eq. (1), and in Fig. 1.
Fig. 1Hologram surface structure
In the case where a plurality of sound sources, the sound source can also be generated by the individual sound pressure vectorially, as shown in Eq. (1):
Eq. (2) the each inter-frequency is independent. In addition to the need for the Doppler shift, the angle of the different sound sources represent different values, the frequency shift is different, and different frequency components between occurred coupling:
The Eq. (2) is to give a continuous spectrum of the wave superposition relationship, for practical computing applications, to be rewritten in the form of discrete:
As shown in Eq. (3), where is the frequency of the microphone, × is the length of sound pressure level of short-vector; is the point source of each short-source, × is the length of intensity of each frequency vector; is a × linear relationship with × transfer matrix columns, as shown in Eq. (4):
where is the point for all frequencies from the sound source to the microphone matrix based on static Green function; is the point for all frequencies from the sound source to the microphone matrix with short-time Doppler shift, or the frequency shift function a discrete approximation, whose first column of the matrix row value of , as shown in Eq. (5):
As known in Eq. (5), according to the discrete spectrum short-wave superimposed [5], when the sound source position and intensity are known, we can calculate the position of any sound pressure frequency domain; if when the receiving point sound source position and sound pressure is known , then in the case of can be obtained by solving equations reverse sound source strength, which analysis of the relationship between sound and source sound field by the use of basic principles of short-wave superimposed.
By calculation of the point source location and strength in the sound source field, due to the sound source field and the reconstruction field remained relatively static, any point sound pressure values inside sound field can be obtained: regularization each sound intensity and then according to the Eq. (5) for simple wave superposition of static sound field, as shown in Eq. (6):
where in the frequency intensity of , is the wave number corresponding to the frequency , is the imaginary unit. Sound pressure spectrum can be obtained, it can be further effective sound pressure values as shown in Eq. (7):
For each point inside reconstruction calculation process repeated, get the reconstruction field sound pressure distribution.
3. Simulation on sound source identification method
Based on the microphones design parameters and the chosen optimization method, and the MLA main lobe area) and SLR (side lobe ratio) were chosen as objective functions, which has mentioned above. In this paper, we set the microphones array type as X, then by optimization method to get the balance of main lobe area value and side lobe ratio through optimize the location of microphones on the X array. The optimization method is shown in Fig. 2.
Fig. 2Model of uniform linear array

Based on the spatial sampling theorem, when the array receives a data (a snapshot), later than the time-space sampling space. In order to ensure the spatial information of the received signal between two array’s elements are needed element spacing should be much greater than the distance accuracy. A fixed cross X-type microphone array as an example describes the plane array performance analysis and process simulation.
Table 1Parameters of array design and performance
Method | WSA | Optimization array |
Parameter | ‘X’array | ‘X’array |
Array distance / m | 3.14 | 3.14 |
Array aperture / m | 0.5 | – |
Microphone quantum | 22 | 20 |
SLR | 0.0385 | 0.0388 |
MLA | 0.0137 | 0.0157 |
In order to validate the algorithm, a simulation experiment is designed as follows. Calculated by simulation of the above two methods to verify the reconstruction effect, the calculation of the 1 sound sources of 1 000 Hz frequency, the surface of which the sound source position coordinates of (0, 0), the original microphone array is comprises by 22, then the optimal microphone array is comprise by 20, which can be seen in Fig. 3, the sound source is stable. Calculation takes between 0.01 s; analyzing frequency is 900-1100 Hz.
Fig. 3Simulation results: a) result of WSA method, b) result of optimization array method
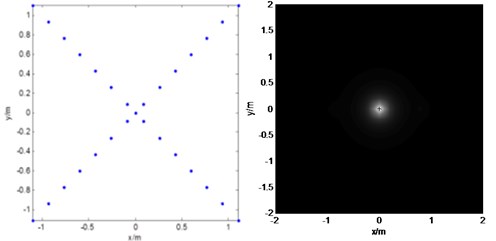
a)
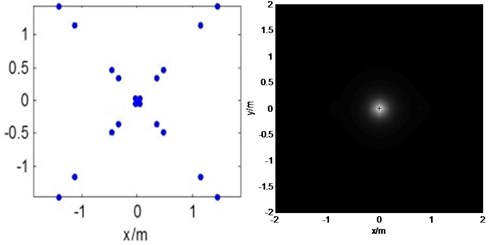
b)
As can be seen from Fig. 3, both kinds of microphones array nearly have the same identification of the sound pressure peaks to get the sound source point, the value SLR and MLA can meet the requirement, the short-wave superposition method results in false sound source has basically been eliminated out.
4. Verified experiment
4.1. Simulation and experiment system
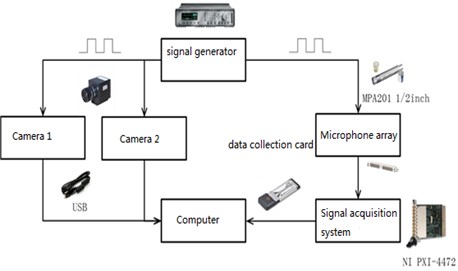
Sound source identification simulation model is established, microphone array where the plane for measurement of the surface, at a distance from the sound source close to the plane to construct a focusing reconstruction, the size of 2×2 m. The rotating wheel array spacing of is 3.14 M, the array aperture is about 0.84 m, consists of 29 microphones, as shown in Fig. 4. In this experiment, microphone array system consists of MPA201 1/2 inch, data acquisition system for NI PXI-4472. Sound source system for single frequency sound files, their voices heard in the sound card of computer and driven sound, forms a single frequency steady-state sound field, and then received by the microphone array sound through the data collection system and by the development of multi-channel signal acquisition software processing. Finally, data is processed using holographic method as shown in Fig. 4.
4.2. Far-field verified experiment
Based on vehicle sound field visualization system, dynamic sound field results comparison can be shown in Fig. 5, which analyzes the target frequency to take 900-1100 Hz. Fig. 5(a) and (b) are there result of the original video images; the dynamic wave super position method based on original microphones array and method based on optimization microphones array respectively to measure the results, the figure abscissa horizontal position coordinates, the vertical axis is the vertical position coordinates, units are m. As can be seen in Fig. 5, the both methods can be captured the sound source, and in the course of the campaign can accurately track their location. The calculated results are shown in Table 2. From the experimental results compare plans and results can be seen in the table, dynamic wave superposition method compared with the different microphones array had nearly the same value of MLA (main sidelobe ratio) and SLR (side lobe ratio).
Fig. 4Simulation model and experiment equipment

a)
b)
Fig. 5Verified experiment results
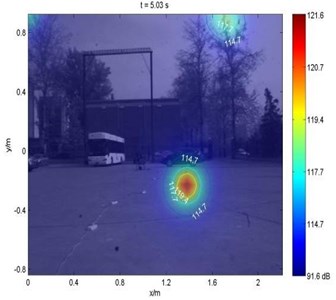
a) Original result: 32 microphones
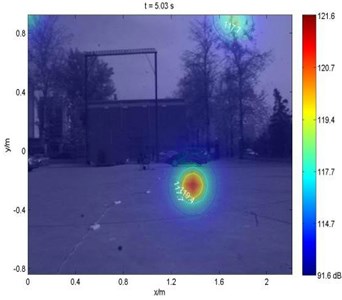
b) Optimization result: 30 microphones
Table 2Parameters of array design and performance
Method | WSA | Optimization array |
Parameter | ‘X’array | ‘X’array |
Array distance / m | 3.14 | 3.14 |
Array aperture / m | 0.5 | – |
Microphone quantum | 29 | 26 |
SLR | 0.1367 | 0.1572 |
MLA | 0.2000 | 0.1900 |
The wave superposition effect is significant for improving the resolution (the main lobe area is decreased). Wave superposition method for the quantitative measurement of single frequency stable sound source is stable. The stability of wave superposition is dependent on the stability of the beam forming pre-recognition results.
According to the theoretical analysis, simulation and experimental results, the advantages of dynamic wave superposition method is effective side lobe suppression effect, can improve the recognition resolution, but this method also has drawbacks, the recognition result of the stability of the pre-dependent recognition result in the beam forming method, the identified sound source position sometimes poor stability, the sound source position appears beating case, further research is needed to improve the stability of the sound source identification.
5. Conclusions
This paper describes and compares the quantitative measured stable vehicle noises measurements in effect two methods, WSA method and WSA method based on optimization array. With the comparison among both methods, the research conclusions are drawn that the wave super position method used optimization which not only provide the same as identification results with original array for locating sound sources accurately but also reduce numbers of microphones and can also solve the ghost sources problem.
However, the application of wave superposition method, there are some problems, such as required in the initial stage, the sound source position estimation, if the error is large pre-recognition results, the method is difficult to improve the recognition effects. In addition, the scope of application of this system is relatively simple, the future should be measured for different needs, consider the application of other forms of microphone array, or normal lens of the camera used to wide-angle lens, expanding measuring range, etc.
References
-
Kook H., Moebs G. B., Davies P., Bolton J. S. An efficient procedure for visualizing the sound field radiated by vehicles during standardized pass by tests. Journal of Sound and Vibration, Vol. 233, 2000, p. 137-156.
-
Takano Y., Terada K., Aizawa F., Iida A., Fujita H. Development of a 2-Dimensional microphone array measurement system for noise sources of fast-moving vehicles. Proceedings of Inter-Noise, Toronto, Canada, 1992, p. 1175-1178.
-
Williams E. G. Supersonic acoustic intensity on plana resources. Journal of the Acoustical Society of America, Vol. 104, Issue 5, 1998, p. 2845-2850.
-
Heilmann Gunnar, Dobler Dirk Time-domain beamforming with zero-padding. 2nd Berlin Beamforming Conference, 2008.
-
Yang D. G., Li B., Wang Z. T., Zheng S. F., Lian X. M. Video visualization for moving sound sources based on binocular vision and short-time beamforming. Noise Control Engineering Journal, Vol. 58, Issue 4, 2010, p. 382-388.
About this article
This work is based on the research of Project 51805229 and Project 51705221, supported by the National Natural Science Foundation of China.
