Research on quantitative mechanism of Kirchhoff diffraction acoustical holography

1. Introduction

Quantitative accuracy and boundary conditions of Kirchhoff diffraction in optics are studied and verified [1]; in which infinite Kirchhoff diffraction model was established and Fresnel wave integral was employed to calculate the quantitative results. The integral results were correlated with the inclination factor and wave front which was determined by integral domain as integration of the surface instead of the aperture plane. Inspired by this work, in our recent study, quantitative accuracy of Kirchhoff diffraction Acoustical Holography was migrated and studied in sound source identification and reconstruction. The relationship between quantitative accuracy of it and the aperture angle (inclination factor) when applied in sound source reconstruction is established.

2. Quantitative mechanism of Kirchhoff diffraction acoustical holography

Kirchhoff diffraction theory is traditional and widely used in optics and acoustics. The classic infinite Kirchhoff diffraction formula is as Eq. (1):

Based on Eq. (1), Kirchhoff diffraction acoustical holography method was established and originally introduced in references [2-4]. According to Kirchhoff diffraction Acoustical Holography principle, the sound pressure distribution in the holographic plane can be reconstructed with Eq. (2):

where $P(\epsilon ,\eta ,f)$ is the frequency domain sound pressure of the point $Q(\epsilon ,\eta )$ in holographic plane, $k=f/c$ is the wave number, $C$ is the holography constant, $r$ is the distance between point $(x,y)$ in measurement plane and $Q(\epsilon ,\eta )$. $U^{\mathrm{*}}(x,y,f)$ is the conjugate sound pressure of point $(x,y)$. From Eq. (1) and Eq. (2), it can be seen that without considering Doppler-effect and discretization error, the main quantitative error theoretically comes from the finite integral domain. In another word, the integral domain error stands for the quantitative accuracy of Kirchhoff diffraction Acoustical Holography.

The Kirchhoff diffraction model of point source is shown in Fig. 1. For the ideal point source model in the free space, the parameters in Eq. (1) are as shown in Fig. 1(a). The strict Kirchhoff diffraction assumes that point source $P$ is located in $(x_1,y_1,z_1)$ which radiates the sound wave conjugated with the wave radiated from the point source in position $P_0(x_0,y_0,z_0)$. If the sound field distribution in the closed spherical surface$S$is obtained, Kirchhoff diffraction can be applied to reconstruct the accurate sound source $P$ with Eq. (1).

Fig. 1Ideal point source model in free space without diffraction: a) complete spherical closed surface, b) finite plane

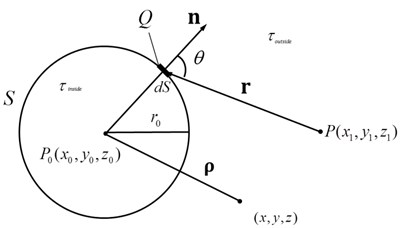
a)

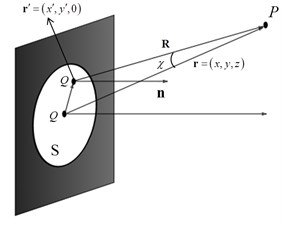
b)

In the practical measurement of two-dimensional microphones-array, the surface S is a finite and discrete plane. For finite Kirchhoff diffraction conditions, Huygens-Fresnel principle and Fresnel diffraction schematic diagram are shown in Fig. 1 (b). Spherical waves are radiated by any secondary point source $Q$ in the plane $S$. $P$ Located in space $\mathbf{r}=\left(x,y,z\right)$, the coordinates of the point source $Q$ is $\mathbf{r}\mathrm{\text{'}}=\left(x\mathrm{\text{'}},y\mathrm{\text{'}},0\right)$. $U\left(x\mathrm{\text{'}},y\mathrm{\text{'}},0\right)$is the sound pressure. $\mathbf{R}$ is the displacement vector from $Q$ to $P$. For point sources, Eq. (3) and Eq. (4) From Eq. (1) as follows:

where $A$ is the sound source amplitude and $\theta$ is the angle between sound source and holographic plane. Then the closed spherical surface and finite planar Kirchhoff diffraction models are separately shown in Fig. 2.

Fig. 2Fresnel’s zone construction algorithm schematic for spherical and planar model: a) complete spherical enclosed surface, b) finite plane

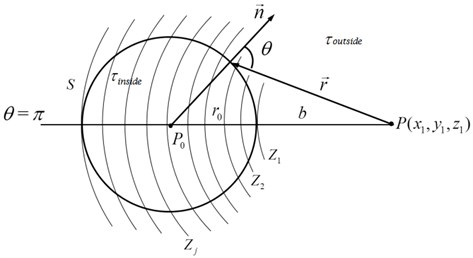
a)

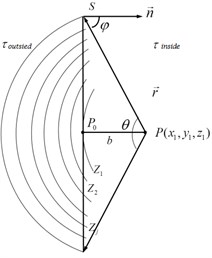
b)

With Eq. (3) and Eq. (4), the original Kirchhoff diffraction formula can be converted into Eq. (5):

where $K_n\left(\theta \right)$ is a dimensionless inclination factor which changes with the angle $\theta$. In Eq. (5), $K_1\left(\theta \right)=$ 1, $K_2\left(\theta \right)=\frac{\mathrm{c}\mathrm{o}\mathrm{s}\theta }{r}$, $K_3\left(\theta \right)=\left(1+\mathrm{c}\mathrm{o}\mathrm{s}\theta \right)$. In order to calculate the integral in Eq. (5), Fresnel’s zone method is applied as shown in Fig. 2. Take point $P$as the centre and $b$, $b+\frac{\lambda }{2}$, $b+\frac{2\lambda }{2}$, $b+\frac{3\lambda }{2}$, ..., $b+\frac{j\lambda }{2}$ as radius to draw a series of spherical surface $Z_1$, $Z_{2.}$, ..., $Z_j$, …, $K_j\left(\theta \right)$ are deemed same between neighbouring $Z_j$ under the condition that the zone is narrow enough. In plane $S$, the differential surface element $dS$ is calculated as Eq. (6):

where $\varphi$ is azimuthal angle round $P_{0}P$ axis. This formula converts into three steps as Eq. (7) shows:

So, the contribution of the $j$th wave zone to $U\left(P\right)$ is:

Calculate the integration, $U_j\left(P\right)$ can be expressed as Eq. (9):

The factor $r^{-2}$ can be neglected in the far field condition, which means that the measurement distance $b$ is more than 20$\lambda$. Under this approximation, the integral result can be converted to Eq. (10):

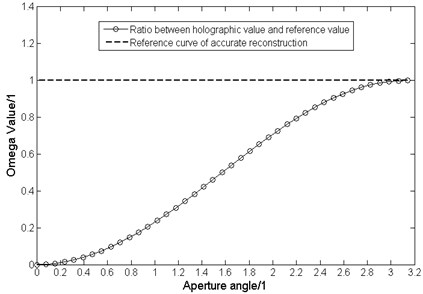
Eq. (10) shows the relative value between the reconstructed holographic result and the theoretical reference value ($\mathrm{\Omega }$). Fig. 3 gives the curve of $\mathrm{\Omega }=\frac{\left|U\left(P\right)\right|}{\left|U_{real}\left(P\right)\right|}$ changing with the aperture angle $\theta$ from 0 to $\pi$.

Fig. 3 shows the calculated quantitative accuracy against the aperture angle.

Fig. 3Curve of ratio between Kirchhoff diffraction acoustical holography value and the reference value changing with aperture angle

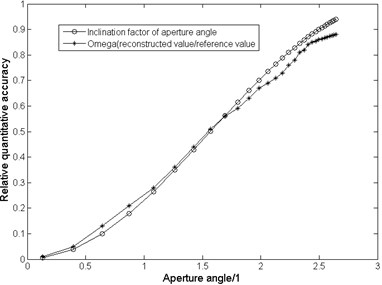
The far-field sound source identification simulation of finite Kirchhoff diffraction is carried out by Huygens-Fresnel theory, and the limit of accurate prediction is studied. A near-uniform grid microphone array measures a 1000 Hz point source at a distance of 2 meters. Table 1 and Fig. 4 show the relationship between the reconstruction result $U\left(P\right)$and the inclination coefficient $k$ considering the aperture angle.

As can be clearly seen from Fig. 4, when the aperture angle increases, the reconstruction results gradually reach the actual value. For tilt factor curves and curves, the fitting of the two curves proves that the critical holographic aperture established in our work is effective for determining the boundary conditions of Kirchhoff diffraction acoustic holography, and the fitting curves are in good agreement with the theory value.

The results can provide the basis for improving the quantitative accuracy of acoustic holography. The reconstruction with a fixed coefficient which can be obtained based on the known sound source.

From the theoretical derivation, the limiting conditions are clear that the sound source must be high-frequency to ensure the Fresnel’s zone is narrow enough for approximation. The microphone array should be extremely close-set to ignore the discretization error, although this will affect the result of flow filed computation greatly.

Fig. 4Comparison of theoretical and experimental values

3. Conclusions

In this paper, the quantitative mechanism of far-field Kirchhoff acoustical holography has been elaborated systematically. Holographic aperture angle is a key factor influencing the quantitative accuracy of acoustical holography.

The results were shown that the spherical wave incident result produced by the wave-front preparation is equivalent to the result of the aperture plane formula at the incident wave plane. The simulation results were shown that the fitting curve of Kirchhoff acoustic holography agrees well with the theoretical value. However, according to the assumptions adopted by our approach, there are still some academic research will be done in the future.