Source localization in reverberation environment based on improved equivalent sound source near-field acoustic holography algorithm

1. Introduction

With the rapid development of computer and other technologies, Monitor Technology of Mechanical Equipment has made remarkable progress in all aspects. Especially in recent years, the advance of acoustic monitoring technology, which has the advantage of non-contact intuitive, attracting a large number of domestic and foreign scholars to pay attention to the research [1]. An important research direction of acoustic monitoring is the location of sound source.

At present, sound source location technology mainly includes: traditional identification method, time-domain analysis method, acoustic holography and beamforming [2], among which acoustic holography method has many advantages such as fast measurement speed, high imaging efficiency and good spatial resolution [3]. However, most of the researches are carried out in free and semi-free acoustic fields such as laboratories with silencer materials or open outdoor areas. These research methods perform better in the free field, but in the reverberation environment, the performance decreases due to the distortion caused by the reflected sound waves from the surrounding walls [4-6]. Most of the mechanical equipment are working in the indoor workshop, engine room and other enclosed space, so the sound source location of this equipment needs to consider environmental noise and reverberation interference factors.

In reverberation environment, the room impulse response represents the acoustic channel from the sound source to the sensor and describes the characteristics of the acoustic environment. Therefore, research on eliminating reverberation interference is generally realized by reducing or directly removing the influence of room impulse response on the received signal. The dereverberation method can be classified into reverberation suppression and reverberation cancellation according to whether or not the impulse response is estimated [7]. Among them, the reverberation cancellation method is based on reverberation estimation and inversion, and the dereverberation problem is regarded as a class of inverse problems. The room impulse response is calculated by analyzing the environment, and then solving inverse of the estimated impulse response to obtain the sound source signal [8].

The principle of reverberation cancellation is the same as the equivalent source method of near-field acoustic holography. In the equivalent source method, the radiated sound field can be expressed as the superposition of sound fields by several equivalent sources (point sources), and the sound source intensity is obtained by inverting the transfer matrix formed by Green’s function of free field, so as to reconstruct the entire sound field [9, 10]. The solution of equivalent source intensity is the key to sound field reconstruction because it is severely ill-conditioned. In order to increase the accuracy and robustness of traditional methods, regularization methods [11-13] were proposed. In addition, [14] introduced the compressive sensing principle and proposed the Compressive-Equivalent Source Method (C-ESM) which effectively improved the positioning accuracy of sound source location.

Zhao estimated the position of the sparse sound source by using the compressed sensing technology, that the dictionary is constructed based on the room impulse response of different positions in space, improving anti-reverberation capability of the positioning algorithm [15]. However, the positioning accuracy of this method is not high, which is related to the spatial grid division.

Considering the problem of reverberation interference in the environment, in the study we take the indoor impulse response as the transfer function to establish the sound source transfer model, estimate the equivalent source intensity through the compressive sensing method, and then reconstruct the sound field through the free field Green’s function. This method can be regarded as a kind of filtering processing, which can eliminate the reflected sound wave interference and improve the sound source location effect of the algorithm under the condition of reverberation.

The rest of this article is organized as follows. Section 2 introduces the basic principle of equivalent source near-field acoustical holography, and the principle of C-ESM estimates the equivalent source strength by compressive sensing method. Section 3 briefly reviews three measurement methods of room impulse response and introduces Image Source Method (ISM) [16] in detail. Section 4 proposes an equivalent source algorithm for reverberation environment based on room impulse response. Section 5 compared and verified the correctness and feasibility of the improved algorithm through COMSOL Multiphysics software simulation modeling, and the final conclusion was given in Section 6.

2. Compressive-equivalent source method (C-ESM)

The equivalent source method (ESM) is a near field sound holographic algorithm with superior performance. The basic idea is to replace the actual sound field by the superposition of the sound field generated by several simple sources. It is critical to obtain the appropriate equivalent source strength by solving the equation based on the sound pressure value of the measuring surface. This is usually an underdetermined problem, which can be solved by Tikhonov regularization. However, this method is easy to be disturbed under low SNR conditions and affects the positioning effect.

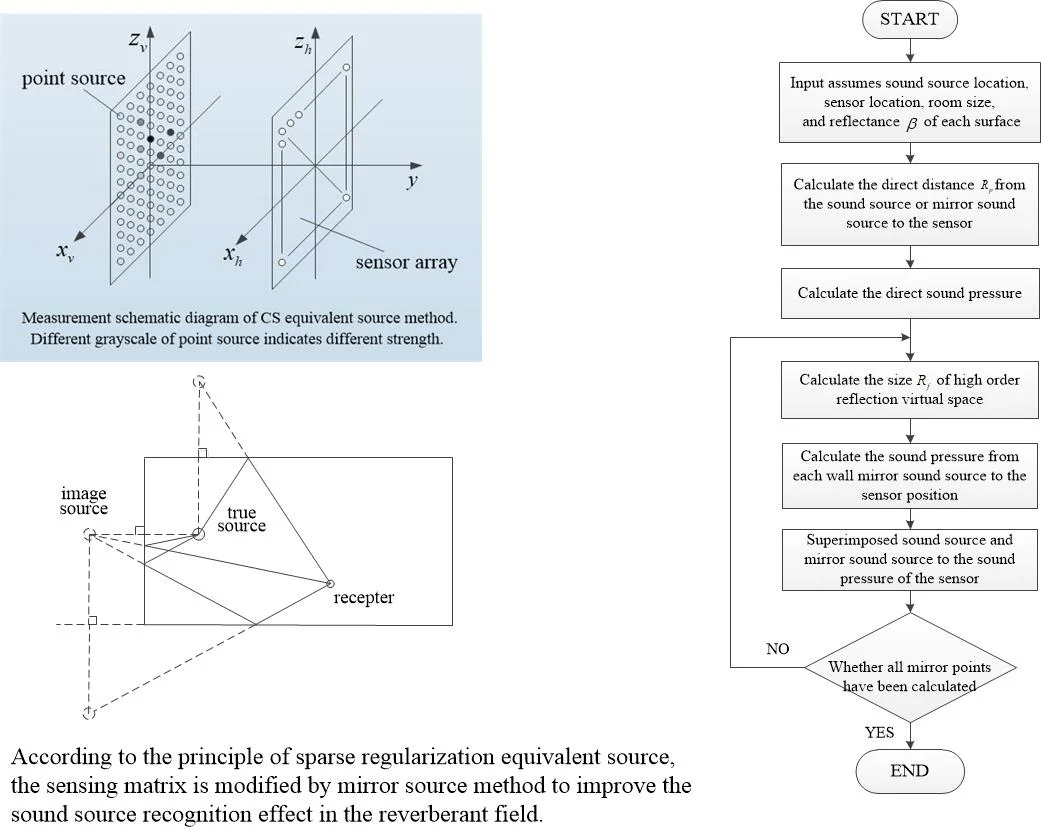
The equivalent source method is to use a series of simple point sources as the equivalent source, which is evenly distributed behind the source, as shown in Fig. 1.

In a free field, the sound pressure on the measuring surface can be regarded as the superposition of the sound pressure propagated by the continuum of sources on the sound source surface:

where $p\left({\mathbf{r}}_h\right)$ denotes the measured surface sound pressure, $q\left({\mathbf{r}}_v\right)$ denotes the equivalent source intensity, $g({\mathbf{r}}_h,{\mathbf{r}}_v)$ denotes the free space Green’s function of the equivalent source to the holographic surface, $\rho$ is the medium density, and $c$ is the speed of sound in the medium. where $k=\omega /c$ and $\omega$ is the angular frequency.

Fig. 1Schematic diagram of equivalent source method principle, where Sv is the equivalent sound source surface, Ss is the real sound source surface, and Sh is the holographic measurement surface

After discretization, it can be expressed as:

where ${\mathbf{Q}}_v=[q_1,\cdots ,q_N{]}^T\in C^N$ is the strength vector of $N$ equivalent sources are uniformly distributed in the sound source, ${\mathbf{P}}_h=\left[p\right(r_1,\omega ),\cdots ,p(r_M,\omega ){]}^T\in C^M$ is thess measured pressure vector by $M$ sensor arrays, and ${\mathbf{r}}_M$ is the position vector of the sensor. ${\mathbf{G}}_{hv}$ is the free-field transfer function from the equivalent source to the sensor array, and the element $G_{hv}(m,n)$ in the matrix represents transfer function from the $n$th equivalent source to the $m$th sensors:

The solution of Eq. (2) is the estimation of equivalent sound source strength, which is the basis of deriving the sound pressure distribution of the whole sound field. However, the number of equivalent sources is generally more than the number of array elements, $N>M$. In this case, Eq. (2) is an underdetermined equation with a non-unique solution.

The solution of Eq. (2) can constitute an optimization problem:

The common method is to solve the ${‖\mathbf{Q}‖}_2$ minimization by Tikhonov regularization and obtain the equivalent source strength. It is simplified as:

However, the selection of regularization parameters $\lambda$ in Ep. (6) needs to know the relative noise level and is greatly affected by the relative noise level.

Compressive sensing technology has great advantages in dealing with the reconstruction of sparse signals. Considering the fact that the sound source is not densely spaced in space and is sparsely spaced. The compressive sensing theory can be applied to the solution of equivalent source strength [17]. In this method, the source surface is equivalent to a number of uniformly distributed point sources, in which the strength of most equivalent sound sources is zero and sparsity exists.

This method considers the sparsity of sound sources in space to solve Eq. (2) under the ${‖\mathbf{Q}‖}_0$ minimization constraint, that is the solution with the minimum number of sound sources in space. It is very difficult to directly solve this problem, but when the problem of research is sparse, the minimization of ${‖\mathbf{Q}‖}_0$ can be relaxed to the ${‖\mathbf{Q}‖}_1$ minimization problem, and the original problem is transformed into:

The above problems can be solved by the convex optimization algorithm, such as Base Pursuit algorithm or Matching Pursuit algorithm. The partial sound radiating field can be simulated accurately by solving the equivalent source strength by compressive sensing. Compared with the traditional equivalent source method, this method has a smaller location error in a larger reconstruction volume, and the broadband sound field can be effectively reconstructed.

3. Establishment of the room impulse response model

In the actual engine room or workshop, the radiated sound wave of a sound source will produce reverberation because of the reflection on the walls, which will bring interference to the location of the sound source. Reverberation can be seen as the superposition of sound waves after multiple reflections in space. Therefore, the signal received by the sensor in the closed environment can be regarded as the convolution of a sound source signal and room impulse response, and plus environmental noise. The relationship between the source signal and the sensor in closed environment can be established by the impulse response.

For the establishment of impulse response function in reverberation environment, several methods are proposed, such as wave-based modeling, ray-based modeling, statistical modeling and so on [18].

The wave-based modeling methods are mainly applied to the simple case such as rigid wall room. This method can obtain an accurate impulse response function to solve the wave equation of the room sound field by the finite element method. But it is difficult to determine the boundary conditions, and the number of computations is large.

The statistical modeling methods, such as the Statistical Energy Analysis, are widely used in high-frequency noise analysis, but this method cannot simulate the change of sound field state with time, and that is not suitable for the auralization of a sound field.

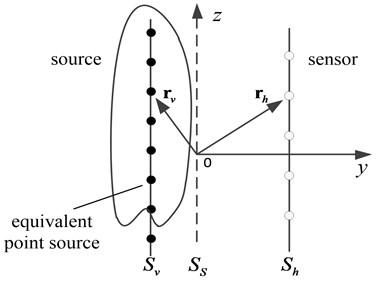
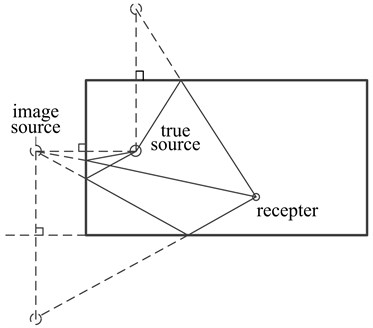
The ray-based modeling methods were developed from geometrical room acoustics. The methods require simulating all possible sound reflection paths from a source to a receiver for an ideal impulse response. Such as the image source method. By setting the mirror source to indicate the source direction of the reflected sound wave, the image source method can calculate the path length of the reflected waves of each level and simulate the sound field environment to obtain the room impulse response [19]. As shown in Fig. 2.

In a cuboid closed environment, the sound wave reaches the sensor position through multiple reflections from the walls, and the discrete signal received by the sensor can be expressed as:

And $t=n\cdot T$, where $T$ is the sampling period, which is the time between the samples, and $n$ is an integer that establishes the time position of each sample. $h\left(n\right)$ is the impulse response function from the sound source $s\left(n\right)$ to the sensor, $\mathrm{*}$ is the convolution operation, and $w\left(n\right)$ is noise.

Fig. 2Reverberation model of enclosed space

After Fourier transform:

Generally, the path length of the reflection can be obtained by calculating the distance between the image source and the sensor. The room impulse response is obtained by superimposing the propagation functions of each direct wave and all reflected wave paths:

where $R=‖{\mathbf{R}}_{\theta }+{\mathbf{R}}_f‖$, ${\mathbf{R}}_p$ is the distance from the sound source or image source to the sensor, and $\theta$ is the eight sound source locations (include image source), where $q$, $j$, $\upsilon$ takes on values 0 or 1, and $\gamma$ is the order of reflection:

The position coordinates of the sound source $S$ is ($x$, $y$, $z$), the sensor position coordinates ($x\mathrm{\text{'}}$, $y\mathrm{\text{'}}$, $z\mathrm{\text{'}}$); ${\mathbf{R}}_f$ is the virtual room size of the high-order reflection:

where ($L_x$, $L_y$, $L_z$) is the size of the room, the range of each element of ($m_x$, $m_y$, $m_z$) is a positive integer set.

In fact, the reflection coefficient of each wall should also be considered. Eq. (10) is amended as:

where ${\beta }_{x,\xi }^{}$ represents the reflection coefficient of two walls in the $x$-axis, $\xi =$ 1 represents the wall close to the origin of the coordinate, and $\xi =$ 2 represents the wall away from the origin of the coordinate, the coefficient being related to the sound absorption coefficient $\alpha$ of the wall material, $\beta =\pm \sqrt{1-\alpha }$.

According to the specific environment, the impulse response from the sound source to any position in the closed space can be obtained through Eq. (13).

4. Equivalent source method based on room impulse response

In the reverberation environment, the acoustic holography algorithm based on compressive sensing is seriously affected by the reflected sound wave interference.

By analyzing the principle of ESM, the improved algorithm replaces the transfer function in the free field with the room impulse response function to describe the signal received by the sensor more accurately, and then reconstructs the sound field through the free-field transfer function to achieve the filtering of the reflected sound wave.

4.1. Constructing the transfer function based on the room impulse response

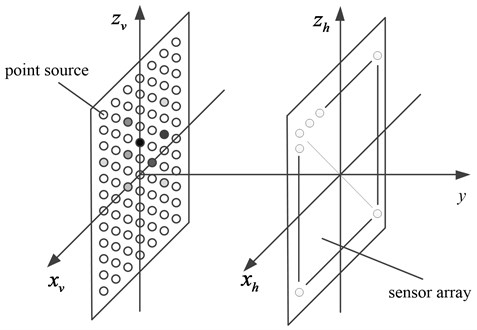
As shown in Fig. 3, it is assumed that $N$ simple sound sources of different intensities are uniformly distributed in the sound source, and the position of the point source is marked as $q_i$. The point source of position $q_i$ to the $m$th array element on the sensor array has a room impulse response of $H_{m,q_i}\left(k\right)$, which together form a reverberation transfer function ${\mathbf{G}}_h\left(k\right)$.

Fig. 3Measurement schematic diagram of CS equivalent source method different grayscale of point source indicates different strength

$H_{m,q_i}\left(k\right)$ is obtained by image sound method, and the specific process is shown in Fig. 4.

Fill the calculated $H_{m,q_i}\left(k\right)$ into Eq. (14), and get ${\mathbf{G}}_h\left(k\right)$:

14

${\mathbf{G}}_h\left(k\right)=\left[\begin{array}{cccc}{H}_{1,q_1}\left(k\right)& H_{1,q_2}\left(k\right)& \cdots & H_{1,q_N}\left(k\right)\\ H_{2,q_1}\left(k\right)& H_{2,q_2}\left(k\right)& \cdots & H_{2,q_N}\left(k\right)\\ ⋮& ⋮& & ⋮\\ H_{M,q_1}\left(k\right)& H_{M,q_2}\left(k\right)& \cdots & H_{M,q_N}\left(k\right)\end{array}\right].$

4.2. Calculate equivalent source strength

The received signal of $M$ sensors can form a vector $\mathbf{X}=[x_1,x_2,\dots ,x_M]$, which is expressed in the wavenumber domain as follows:

15

$\mathbf{X}\left(k\right)={\mathbf{G}}_h\left(k\right)\mathbf{S}\left(k\right)+\mathbf{W}\left(k\right),$

where $\mathbf{W}\left(k\right)$ represents environmental noise. The Eq. (15) is consistent with the Eq. (2), and the number of equivalent sources is sparse in the spatial domain. The equivalent source strength vector $\mathbf{S}\left(k\right)$ can be reconstructed by the method of compressive sensing, and the elements of the vector $\mathbf{S}\left(k\right)$ represent the strength of the equivalent sound source at different locations.

Fig. 4A flow diagram for constructing the impulse response function from a sound source point to the sensor

The equivalent source strength can be solved by solving the following equation:

16

$\left\{\begin{array}{l}\mathrm{m}\mathrm{i}\mathrm{n}{‖\mathbf{S}‖}_0,\\ s.t.\mathrm{}\mathrm{}\mathrm{}\mathrm{}{‖\mathbf{X}-{\mathbf{G}}_h\mathbf{S}‖}_2^{}\le \epsilon .\end{array}\right.$

This paper uses orthogonal matching pursuit algorithm to solve [20], and the general steps are as follows:

1. Initialization: ${\mathbf{r}}_0=\mathbf{X}$, ${\mathrm{\Lambda }}_0=\mathrm{Ø}$, $G_h=Ø$, $t=$ 1;

2. Search index ${\lambda }_t$: ${\lambda }_t=\mathrm{a}\mathrm{r}\mathrm{g}\underset{j=\mathrm{1,2},\cdots ,N}{\mathrm{m}\mathrm{a}\mathrm{x}}\left|⟨{\mathbf{r}}_{t-1},{\mathbf{\alpha }}_j⟩\right|$;

3. Settings ${\mathrm{\Lambda }}_t={\mathrm{\Lambda }}_{t-1}\cup \left\{{\lambda }_t\right\}$, ${\mathbf{G}}_{h,t}={\mathbf{G}}_{h,t-1}\cup {\mathbf{\alpha }}_{{\lambda }_t}$;

4. Find the least squares solution of $\mathbf{X}={\mathbf{G}}_{h,t}{\mathbf{\theta }}_t$:${\widehat{\mathbf{\theta }}}_t=\mathrm{a}\mathrm{r}\mathrm{g}\underset{{\theta }_t}{\mathrm{m}\mathrm{i}\mathrm{n}}‖\mathbf{X}-{\mathbf{G}}_{h,t}{\mathbf{\theta }}_t‖$;

5. Update residual: ${\mathbf{r}}_t=\mathbf{X}-{\mathbf{G}}_{h,t}{\widehat{\mathbf{\theta }}}_t$;

6. Judge $‖{\mathbf{r}}_t‖\le \epsilon$, if true, outputs the estimated value ${\widehat{\mathbf{\theta }}}_t$ of $\mathbf{S}$, otherwise it returns to step 2.

5. Simulation experiment

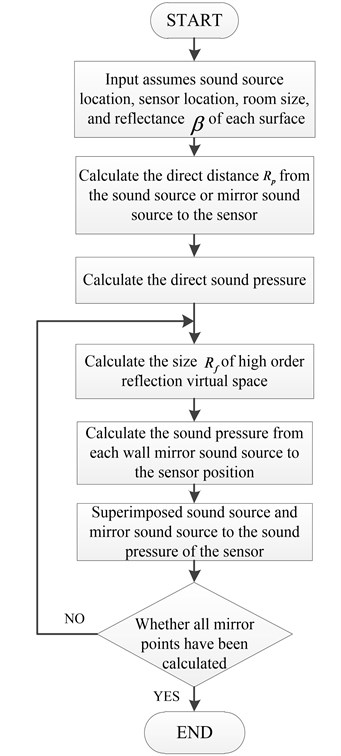
The experiment simulates the near-field acoustic radiation environment generated by metal disk under excitation force. The reverberant field model (Fig. 5) in the closed rectangular space and the free sound field model (Fig. 6) were established respectively. In the model of free sound field, all boundaries absorb sound waves completely without any reflection. In the reverberation model, the sound reflection coefficient of boundaries is set in accordance with Table 1. The setting parameters of the two models are identical except the boundary condition.

Fig. 5The reverberation sound field model

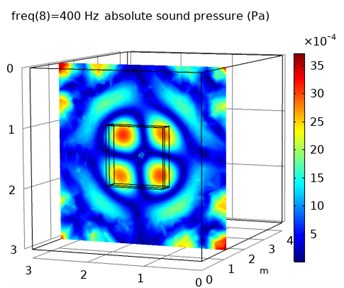
Fig. 6The free sound field model

Set a rectangular parallelepiped space with a length, width and height of 3×4×3 m, with the corner of the cuboid as the origin, and the edge line as the coordinate system to establish the coordinate system, and fill air in the space. Place a disc with a radius of 0.05 m and a thickness of 0.01 m at the (1.5, 1, 1.5) point of the room. The material of the disc is structural steel. The edge of the disc is fixed, and the sound field is generated by applying an excitation force at its center. The excitation force is comprising a series of harmonic signals over a frequency range of 50-2000 Hz and an interval of 50 Hz.

The pressure acoustic simulation environment was selected for simulation calculation in COMSOL Multiphysics software. The simulation model is divided with the free tetrahedral mesh, the frequency domain compilation equation is selected for compilation, and the steady-state solver is used to solve the equation.

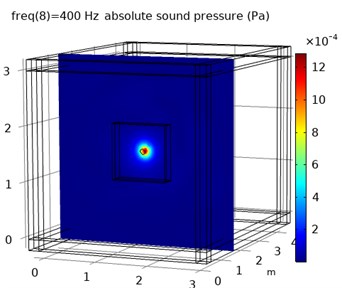
Fig. 7Data collection array

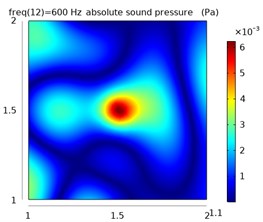
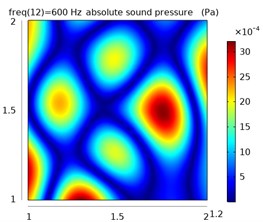
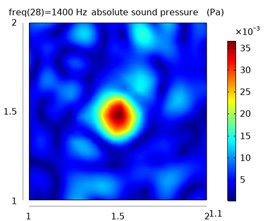
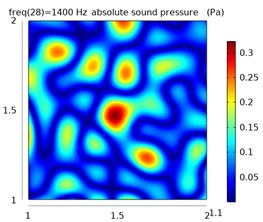
Fig. 8The sound pressure distribution at different frequencies in the free field and reverberation field

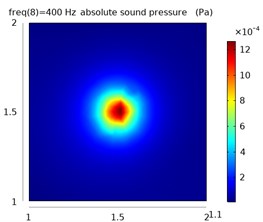
a)

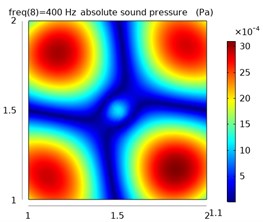
b)

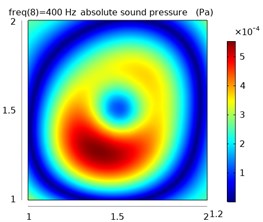
c)

d)

e)

f)

g)

h)

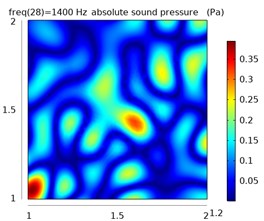
i)

The left column represents the sound pressure distribution at $y=$ 1.1 m in the free field, and the other two columns represent the sound pressure distribution at $y=$ 1.1 m and $y=$ 1.2 m in the reverberation field.

At a position 0.2 m away from the disk, a data collection array is placed to collect the sound pressure data in the sound field, as shown in Fig. 7. The spacing of array elements is 0.05 m, and the number of array elements is 21×21. The sound pressure value in the sound field is collected by the array.

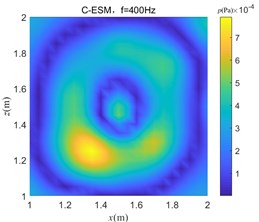
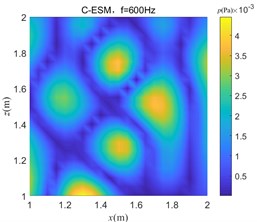
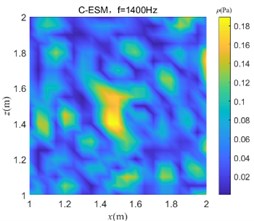
From the simulation data, the sound pressure distribution of the plane at $y=$ 1.1 m is obtained in the free field environment and the reverberation environment at 400 Hz, 600 Hz, and 1400 Hz, as shown in Fig. 8.

It can be seen from the distribution of sound pressure that the reverberation seriously interferes with the judgment of the position of the sound source. As the frequency increases, the sound pressure distribution becomes more complicated, the sound wave has stronger directivity, and the reflection efficiency increases in the closed space, which makes the distribution of sound pressure in the space more confusing, and it is difficult to judge the sound source position.

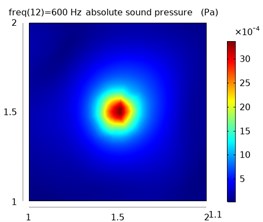
Fig. 9 shows sound pressure distribution images at 400 Hz, 600 Hz, and 1400 Hz, which are obtained by processing the sound pressure data collected in the reverberant field by the C-ESM method and the improved method, respectively, and thereby determining the sound source position. The equivalent source number of both methods is set to 31×31.

Fig. 9Sound pressure image at y= 1.1 m obtained by the two algorithms

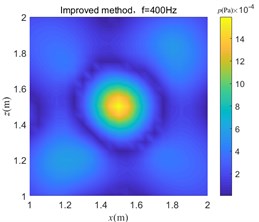
a)

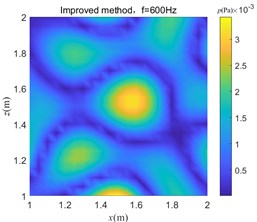
b)

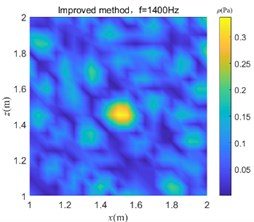
c)

d)

e)

f)

It can be seen from Fig. 9 that the sound pressure distribution image obtained by the C-ESM algorithm determines that the sound source position will cause a serious positional deviation, and the positioning method fails. The sound pressure image obtained by the improved algorithm more accurately indicates the sound source position, that is, the hot spot position of the sound pressure image can be discriminated as the sound source position, indicating that the algorithm effectively removes the environmental reverberation interference. The improved algorithm is suitable for sound source localization in a reverberant environment.

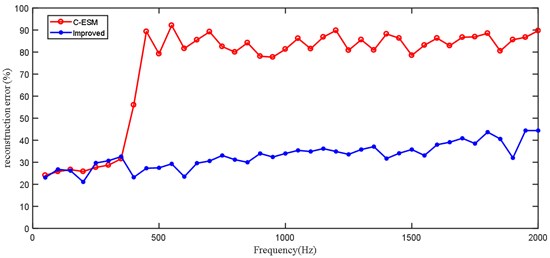
In order to compare the reconstructed sound pressure with the value of the sound pressure in the free field, Eq. (19) is used to describe the reconstruction error quantitatively, which reflects the approximate degree of the sound pressure value on the whole:

where $p_t$ represents the reconstructed sound pressure value matrix, and $p_r$ represents the sound pressure value matrix measured in the free field environment. According to Eq. (19), the reconstruction errors of the two methods at 50-2000 Hz frequency are obtained, as shown in Fig. 10. If the reconstruction error is less than 30 %, the sound source location can be clearly identified, indicating that the reconstruction is more accurate, and the misjudgment location will occur when the error is more than 40 %.

It can be seen that in the reverberation environment, the C-ESM method still has limited localization effect at low frequencies. However, as the frequency increases, the algorithm cannot accurately determine the location of the sound source. Especially when the frequency is higher than 350 Hz, the original algorithm completely fails.

In a wide frequency band, the reconstruction error of the improved algorithm is about 30 %, and the sound source location can be determined stably and accurately. This algorithm has obvious advantages in the location of sound source in reverberation environment, but with the increase of frequency, the location effect decreases, and the location of sound source will be misjudged.

Fig. 10Reconstruction error at different frequencies

6. Conclusions

The localization of sound source in a reverberant environment is studied，based on the equivalent source method of near-field sound holography. By modifying the construction of the transfer matrix, the accuracy of solving the equivalent source strength is improved. Then, the sound pressure field distribution without reverberation interference is deduced by using the transfer function constructed by the free-field transfer function, so as to direct the location of the sound source. The whole process of the algorithm can be seen as filtering the reverberation interference, leaving only the direct wave signal and reconstructing the free environment sound field.

Theoretical analysis and simulation results show that, compared with the C-ESM method, in the reverberation environment, the improved algorithm can accurately guide the location judgment of sound source in a wide frequency range, broaden the application scope of the C-ESM method, and is an exploration of the application in the actual engineering environment. However, in general, the reconstruction error will increase with the increase of frequency, and the situation of the high-frequency band needs further improvement.