Three-dimensional biological tissue under high-order effect of two-temperature thermal lagging to thermal responses due to a laser irradiation

Youssef, Hamdy M.; Alghamdi, Najat A.

doi:10.21595/vp.2019.20521

Vibroengineering Procedia

Browse Procedia

Published: 15 March 2019

Check for updates

Three-dimensional biological tissue under high-order effect of two-temperature thermal lagging to thermal responses due to a laser irradiation

Hamdy M. Youssef¹

Najat A. Alghamdi²

^{1, 2}Umm Al-Qura University, Makkah, Saudi Arabia

Corresponding Author:

Hamdy M. Youssef

Cite the article Download PDF

Downloads 1450

CrossRef Citations 4

Abstract

Using the lasers and heat transfer through biological skin tissue is essential for the processes of the medical treatment. Thus, two-temperature bio-heat transfer equations were introduced and used to discuss the variation of temperature in a laser-irradiated biological tissue. As a result, the Laplace and Fourier transform techniques have been applied, and the solutions of the conductive temperature have been represented in figures. The two-temperature parameter, the penetration depth parameter, the dimensions of the rectangular laser pulse, and the power density of laser irradiation parameter have significant effects on the thermal waves through the skin tissue.

1. Introduction

In the medical applications, the use of lasers has increased over the past half-century. For increasing the therapy quality, the observation of thermal damage is important. Effect of the laser irradiation on the biological tissues takes different types. The most common of those applications include the thermal effects. The thermal interaction is the most important since temperature rising due to thermal effects is a final factor to produce thermal damage. Due to lack of knowledge about the thermal reaction and response, the clinical doctors could not control the times of using the laser power [1-4]. To predict the thermal damage quantity, it is required to study the thermal response caused by the laser energy deposition. As a result, the analysis of thermal transport is essential to make an improvement to the treatment qualification and for more safety. The experiment is an essential method to know the medical treatment problems [4, 5]. The most famous researchers studied the bioheat transfer in the biological skin tissues are Pennes [6], Abramson [7]. The Pennes bio-heat transfer equation is used to simulate and model the thermal behavior in the biological bodies. The review paper [8] represented many attempts to model the thermal behavior of the human body. Xu et al. [9, 10] presented a system discussion to the DPL effects on the bio-thermo-mechanical behavior of skin tissues. The linear DPL equation has been used in various theoretical studies [11-13]. Youssef applies the two-temperature heat conduction in many applications [14, 15].

2. Materials and method

Consider homogeneous skin tissue in three-dimensional fills the region $Ψ$ which is defined by $Ψ = \{x, y, z : 0 \leq x < \infty, - \infty < y < \infty, - \infty < z < \infty\}$ where the skin is initially at rest and has been thermally shocked by laser irradiation with a rectangular pulse at the bounding plane to the surface. Tzou proposed the DPL model in the classical heat flux model as [16]. Youssef proposed the two-temperature model to differentiate between the conductive temperature and the dynamical temperature as [17].

1

K (1 + τ_{T} \frac{\partial}{\partial t} + \frac{τ_{T}^{2}}{2} \frac{\partial^{2}}{\partial t^{2}}) \nabla^{2} T_{C} = (1 + τ_{q} \frac{\partial}{\partial t} + \frac{τ_{q}^{2}}{2} \frac{\partial^{2}}{\partial t^{2}}) [ρ C \frac{\partial T_{D}}{\partial t} + W_{b} C_{b} ρ_{p} (T_{D} - T_{b}) - (Q_{m e t} + Q_{e x t})],

where $T$ is the temperature, $K$ the heat conductivity, $t$ is the time, $τ_{q}$ , $τ_{T}$ are the phase lag of the heat flux and the phase lag of the temperature gradient, respectively, $ρ$ is the density, $C$ is the specific heat, $C_{b}$ and $W_{b}$ are the specific heat and perfusion rate of blood. $Q_{m e t}$ is the metabolic heat generation and $Q_{e x t}$ is the heat source for spatial heating, $T_{b}$ is the arterial temperature, $T_{C}$ is the conductive temperature, and $T_{D}$ is the dynamical temperature:

2

T_{C} - T_{D} = β \nabla^{2} T_{C},

where $β$ is a non-negative parameter which is called two-temperature parameter.

The term $W_{b} C_{b} (T_{D} - T_{b})$ expresses the heat caused by convection within the head per unit mass of the tissue and it is considered to be homogenous.

Assume the functions $φ$ and $θ$ is as follows:

3

φ (x, y, z, t) = T_{C} (x, y, z, t) - T_{b}, θ (x, y, z, t) = T_{D} (x, y, z, t) - T_{b} .

From Eqs. (1) and (2), we obtain:

4

K (1 + τ_{T} \frac{\partial}{\partial t} + \frac{τ_{T}^{2}}{2} \frac{\partial^{2}}{\partial t^{2}}) \nabla^{2} φ = (1 + τ_{q} \frac{\partial}{\partial t} + \frac{τ_{q}^{2}}{2} \frac{\partial^{2}}{\partial t^{2}}) [ρ C \frac{\partial θ}{\partial t} + W_{b} C_{b} ρ_{p} θ - (Q_{m e t} + Q_{e x t})],

5

θ = φ - β \nabla^{2} φ,

where $\nabla^{2} = (\frac{\partial^{2}}{\partial x^{2}} + \frac{\partial^{2}}{\partial y^{2}} + \frac{\partial^{2}}{\partial z^{2}})$ .

Due to the chemical reactions within the tissues, the metabolic heat source is valid, and it is assumed to be a constant $Q_{m e t} =$ 368.1 W/m³. When the laser beam shocked the skin surface, the laser energy is absorbed, scattered, and transmitted. Lambert expresses the laser power intensity along the tissue depth-Beer’s law, as follows [2]:

6

I (x, y, z, t) = I_{0} e^{- δ x} H (t) H (a - |y|) H (b - |z|)

Heat generation due to scattering is assumed to be negligible; therefore, the specific absorption rate in the target zone can be expressed as follows:

7

- \frac{\partial I}{\partial x} = Q_{e x t} (x, y, z, t) = l I_{0} e^{- δ x} H (t) H (a - |y|) H (b - |z|) .

In the Eq. (6), $I_{0}$ (W/m²) represents the power density of laser irradiation and $H (t)$ is the Heaviside unit step function. The parameter $δ$ represents the penetration depth. It means, the rectangular thermal pulse of the laser irradiation acts on a band of width 2 $a$ centered on the $y$ -axis and 2 $b$ centered around the $z$ -axis on the surface of the half-space $x = 0$ and is zero elsewhere:

8

K (1 + τ_{T} \frac{\partial}{\partial t} + \frac{τ_{T}^{2}}{2} \frac{\partial^{2}}{\partial t^{2}}) \nabla^{2} = (1 + τ_{q} \frac{\partial}{\partial t} + \frac{τ_{q}^{2}}{2} \frac{\partial^{2}}{\partial t^{2}})

∙ (ρ C \frac{\partial θ}{\partial t} + W_{b} C_{b} ρ_{p} θ - (l I_{0} e^{- δ x} H (t) H (a - |y|) H (b - |z|) + Q_{m e t})) .

Applying the Laplace transform for Eqs. (5), (7) and (8) defined as:

9

\bar{f} (s) = \int_{0}^{\infty} f (t) e^{- s t} d t,

where:

10

{φ (x, t)|}_{t = 0} = {θ (x, t)|}_{t = 0} = {\frac{\partial φ (x, t)}{\partial t}|}_{t = 0} = {\frac{\partial θ (x, t)}{\partial t}|}_{t = 0} = 0 .

Thus, we get:

11

K h_{T} \nabla^{2} \bar{φ} = h_{q} (ρ C s + W_{b} C_{b} ρ_{p}) \bar{θ} - \frac{Q_{m e t} h_{q}}{s} - \frac{h_{q} δ I_{0}}{s} H (a - |y|) H (b - |z|) e^{- δ x},

12

\bar{θ} = \bar{φ} - β \nabla^{2} \bar{φ},

where $h_{T} = (1 + s τ_{T} - \frac{s^{2} τ_{T}^{2}}{2})$ , $h_{q} = (1 + s τ_{q} - \frac{s^{2} τ_{q}^{2}}{2})$ .

3. The governing equations in the Fourier transform domain

Using double Fourier transform for any function $f (x, y)$ which is defined as follows:

20

F [\bar{f} (x, y, z, s)] = \tilde{\bar{f}} (x, p, q, s) = \frac{1}{2 π} \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} \bar{f} (x, y, z, s) e^{- i (p y + q z)} d y d z,

where the inversion transform of the double Fourier transform takes the form:

21

F^{- 1} [\tilde{\bar{f}} (x, p, q, s)] = \bar{f} (x, y, z, s) = \frac{1}{2 π} \int_{- \infty}^{\infty} \int_{- \infty}^{\infty} \tilde{\bar{f}} (x, p, q, s) e^{i (p y + q z)} d p d q,

Hence, we have:

23

(\frac{\partial^{2} \tilde{\bar{φ}}}{\partial x^{2}} - p^{2} \tilde{\bar{φ}} - q^{2} \tilde{\bar{φ}}) = \frac{h_{q} (ρ C s + W_{b} C_{b} ρ_{p})}{K h_{T}} \tilde{\bar{θ}}

- \frac{2 δ I_{0} h_{q} s i n (p a) s i n (q b)}{π s p q K h_{T}} e^{- δ x} - \frac{Q_{m e t} h_{q} δ (p) δ (q)}{s K h_{T}},

24

\tilde{\bar{θ}} = [1 + β (p^{2} + q^{2})] \tilde{\bar{φ}} - β \frac{\partial^{2} \tilde{\bar{φ}}}{\partial x^{2}} .

By eliminating $\tilde{\bar{θ}}$ from Eqs. (15) and (16), we get the following differential equation:

25

\frac{\partial^{2} \tilde{\bar{φ}} (x, s)}{\partial x^{2}} - λ^{2} \tilde{\bar{φ}} (x, s) = - k_{1} e^{- l x} - k_{2}, 0 \leq x \leq L

where:

λ^{2} = \frac{h_{q} (ρ C s + W_{b} C_{b} ρ_{p}) (1 + β (p^{2} + q^{2})) + K h_{T} (p^{2} + q^{2})}{[K h_{T} + β h_{q} (ρ C s + W_{b} C_{b} ρ_{p})]},

k_{1} = \frac{2 δ I_{0} s i n (p a) s i n (q b) h_{q}}{π s p q (K h_{T} + β h_{q} (ρ C s + W_{b} C_{b} ρ_{p}))}, k_{2} = \frac{Q_{m e t} δ (p) δ (q) h_{q}}{s (K h_{T} + β h_{q} (ρ C s + W_{b} C_{b} ρ_{p}))} .

The general solution of the differential Eq. (17) takes the form:

26

\tilde{\bar{φ}} (x, p, q, s) = c_{1} e^{λ x} + c_{2} e^{- λ x} - \frac{k_{1}}{δ^{2} - λ^{2}} e^{- δ x} + \frac{k_{2}}{λ^{2}}, 0 \leq x \leq L,

where $c_{1}$ and $c_{2}$ are some parameters which have to be determined.

Apply the boundary conditions:

27

{\frac{\partial \tilde{\bar{φ}} (x, p, q, s)}{\partial x}|}_{x = 0} = - Q_{e x t} (0, y, z, t) = - q_{0}, {\frac{\partial \tilde{\bar{φ}} (x, p, q, s)}{\partial x}|}_{x = L} = 0 .

Hence, we obtain:

28

\tilde{\bar{φ}} (x, p, q, s) = k_{3} c o s h λ (L - x) - k_{4} c o s h λ x - \frac{k_{1}}{(δ^{2} - λ^{2})} e^{- δ x} + \frac{k_{2}}{λ^{2}}, 0 \leq x \leq L,

where:

k_{3} = \frac{1}{λ s i n h λ L} (\frac{δ k_{1}}{(δ^{2} - λ^{2})} + q_{0}), k_{4} = \frac{δ k_{1} e^{- δ L}}{λ (δ^{2} - λ^{2}) s i n h λ L} .

4. Results

The values of the relevant thermal parameters used in the present calculations are as follows in Table 1 [4, 9, 13, 18].

Table 1The material properties of the skin tissue

Parameter	Unit	Skin tissue	Parameter	Unit	Skin tissue
$K$	W/m°C	0.628	$W_{b}$	ml/Cm	0.00187
$ρ$	kg/m³	1000	$T_{b}$	°C	37
$ρ_{b}$	kg/m³	1060	$τ_{T}$	s	10
$C$	J/kg°C	4187	$τ_{q}$	s	15
$C_{b}$	J/kg°C	3860	$L$	m	0.05

5. Discussion

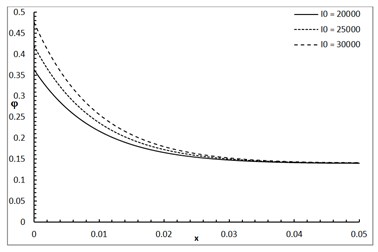
Fig. 1 shows the conductive temperature increment with a range of $x$ -axis and various positions of $y$ and $z$ . The values of both $y$ and $z$ have significant effects. When the values of $y$ and $z$ are increasing, the value of the conductive temperature increment is decreasing. Fig. 2 shows the conductive temperature increment with a range of $x$ -axis and various value of $β$ and $y = z =$ 0.0. The value of $β$ has a significant effect. When the value of $β$ is increasing, the value of the conductive temperature is increasing. Fig. 3 shows the conductive temperature distribution with a range of $x$ -axis and various value of $δ$ when $y = z =$ 0.0. The value of $δ$ has a significant effect. When $δ$ is decreasing, the value of the conductive temperature is decreasing. Fig. 4 shows the conductive temperature distribution with a range of $x$ -axis and various $a$ , $b$ and $y = z =$ 0.0. The values of $a$ and $b$ have significant effects. When the values of $a$ and $b$ are increasing, the value of the conductive temperature is increasing. Fig. 5 shows the conductive temperature distribution with a range of $x$ -axis and various value of $I_{0}$ when $y = z =$ 0.0. The value of $I_{0}$ has a significant effect. When the value of $I_{0}$ is increasing, the value of the conductive temperature is increasing.

Fig. 1The conductive temperature increment with various of y, z

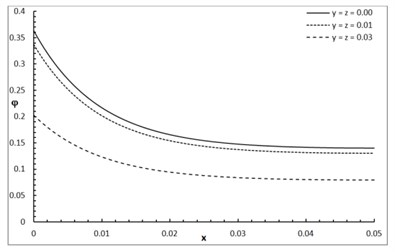
Fig. 2The conductive temperature increment distribution with various values of β

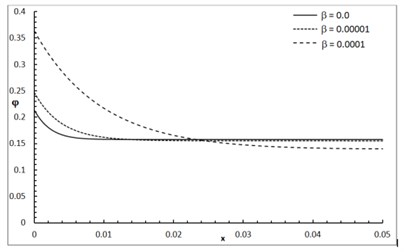
Fig. 3The conductive temperature increment distribution with various values of δ

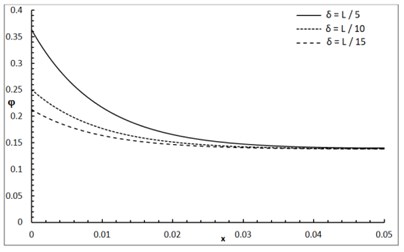
Fig. 4The conductive temperature increment distribution with various of a and b

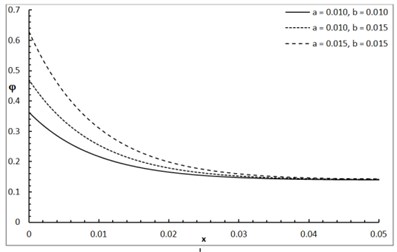
Fig. 5The conductive temperature increment with various of I0

6. Conclusions

The two-temperature parameter, the dimensions of the rectangular laser pulse, the penetration depth parameter, and the power density of laser irradiation have significant effects on the conductive temperature.

References

Liu K.-C., Wang J.-C. Analysis of thermal damage to laser irradiated tissue based on the dual-phase-lag model. International Journal of Heat and Mass Transfer, Vol. 70, 2014, p. 621-628.

Publisher
Welch A. The thermal response of laser irradiated tissue. IEEE Journal of Quantum Electronics, Vol. 20, Issue 12, 1984, p. 1471-1481.

Publisher
Díaz S. H., Nelson J. S., Wong B. J. Rate process analysis of thermal damage in cartilage. Physics in Medicine and Biology, Vol. 48, Issue 1, 2002, p. 19.

Publisher
Zhou J., Chen J., Zhang Y. Theoretical analysis of thermal damage in biological tissues caused by laser irradiation. Molecular and Cellular Biomechanics, Vol. 4, Issue 1, 2007, p. 27.

Search CrossRef
Liu K.-C. Analysis for high-order effects in thermal lagging to thermal responses in biological tissue. International Journal of Heat and Mass Transfer, Vol. 81, 2015, p. 347-354.

Publisher
Pennes H. H. Analysis of tissue and arterial blood temperatures in the resting human forearm. Journal of Applied Physiology, Vol. 1, Issue 2, 1948, p. 93-122.

Publisher
Edwards E. A. Circulation in the extremities. JAMA, Vol. 203, Issue 10, 1968, p. 896-896.

Publisher
Bhowmik A., Singh R., Repaka R., Mishra S. C. Conventional and newly developed bioheat transport models in vascularized tissues: A review. Journal of Thermal Biology, Vol. 38, Issue 3, 2013, p. 107-125.

Publisher
Xu F., Lu T., Seffen K., Ng E. Mathematical modeling of skin bioheat transfer. Applied Mechanics Reviews, Vol. 62, Issue 5, 2009, p. 050801.

Publisher
Xu F., Wang P., Lin M., Lu T., Ng E. Quantification and the underlying mechanism of skin thermal damage: a review. Journal of Mechanics in Medicine and Biology, Vol. 10, Issue 3, 2010, p. 373-400.

Publisher
Liu K.-C., Chen H.-T. Analysis for the dual-phase-lag bio-heat transfer during magnetic hyperthermia treatment. International Journal of Heat and Mass Transfer, Vol. 52, Issues 5-6, 2009, p. 1185-1192.

Publisher
Liu K.-C., Wang Y.-N., Chen Y.-S. Investigation on the bio-heat transfer with the dual-phase-lag effect. International Journal of Thermal Sciences, Vol. 58, 2012, p. 29-35.

Publisher
Zhou J., Chen J., Zhang Y. Dual-phase lag effects on thermal damage to biological tissues caused by laser irradiation. Computers in Biology and Medicine, Vol. 39, Issue 3, 2009, p. 286-293.

Publisher
Youssef H. M., Alghamdi N. Thermoelastic damping in nanomechanical resonators based on two-temperature generalized thermoelasticity theory. Journal of Thermal Stresses, Vol. 38, Issue 12, 2015, p. 1345-1359.

Publisher
Youssef H. M., El Bary A. Two-temperature generalized thermo-elastic medium thermally excited by time exponentially decaying laser pulse. International Journal of Structural Stability and Dynamics, Vol. 16, Issue 3, 2016, p. 1450102.

Publisher
Tzou D. Y. Macro-To Microscale Heat Transfer: the Lagging Behavior. John Wiley and Sons, 2014.

Publisher
Youssef H. M. Theory of two-temperature-generalized thermoelasticity. IMA Journal of Applied Mathematics, Vol. 71, Issue 3, 2006, p. 383-390.

Publisher
Xu F., Lu T., Seffen K. Biothermomechanics of skin tissues. Journal of the Mechanics and Physics of Solids, Vol. 56, Issue 5, 2008, p. 1852-1884.

Publisher

Cited by

Mathematical Modelling with the Exact Solution of Three Different Bioheat Conduction Models of a Skin Tissue Shocked by Thermoelectrical Effect

Eman A. N. Al-Lehaibi | Yingchao Su

(2023)

Irreversible thermal damage due to a laser pulse on the human breast tumour

Hamdy M. Youssef | Najat A. Alghamdi

(2022)

The dual-phase-lag bioheat transfer of a skin tissue subjected to thermo-electrical shock

Hamdy M. Youssef | Raafat A. A. Salem

(2022)

The exact analytical solution of the dual-phase-lag two-temperature bioheat transfer of a skin tissue subjected to constant heat flux

Hamdy M. Youssef | Najat A. Alghamdi

(2020)

About this article

Received

14 January 2019

Accepted

21 January 2019

Published

15 March 2019

SUBJECTS

Biomechanics and biomedical engineering

DOI

https://doi.org/10.21595/vp.2019.20521

Keywords

two-temperature

thermal lagging

biological tissue

laser irradiation

Acknowledgements

The authors are grateful for the support of this work as a part of the project provided by the “Long-Term Comprehensive National Plan for Science, Technology, and Innovation” through STU of Umm Al-Qura University by Grant Number 14-MAT162-10.

This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.

Previous article in issue Previous Next article in issue Next

Research article

2022 10 25

The dual-phase-lag bioheat transfer of a skin tissue subjected to thermo-electrical shock

Hamdy M. Youssef, Raafat A. A. Salem

Research article

2021 10 12

Heat transfer and the influence of electromagnetic field and thermal time during temperature distribution in human tissue

Khaled Lotfy, Alla El-Bary

Research article

2021 09 13

Hyperbolic two-temperature generalized thermoelasticity with fractional order strain of solid cylinder

Alaa A. El-Bary

Research article

2019 03 15

Adomian’s decomposition method to modeling power functionally graded thermoelastic materials in heat transfer and thermal stress analysis

Hamdy M. Youssef, Eman A. N. Al-Lehaibi

H. M. Youssef and N. A. Alghamdi, “Three-dimensional biological tissue under high-order effect of two-temperature thermal lagging to thermal responses due to a laser irradiation,” Vibroengineering PROCEDIA, Vol. 22, pp. 112–117, Mar. 2019, https://doi.org/10.21595/vp.2019.20521

Copy Extrica

Copied to clipboard!

TY  - JOUR
DO  - 10.21595/vp.2019.20521
UR  - https://doi.org/10.21595/vp.2019.20521
TI  - Three-dimensional biological tissue under high-order effect of two-temperature thermal lagging to thermal responses due to a laser irradiation
T2  - Vibroengineering PROCEDIA
AU  - Youssef, Hamdy M.
AU  - Alghamdi, Najat A.
PY  - 2019
DA  - 2019/03/15
PB  - JVE International Ltd.
SP  - 112-117
VL  - 22
SN  - 2345-0533
SN  - 2538-8479
ER  - 

Copy Ris

Copied to clipboard!

@article{Youssef_2019,
	doi = {10.21595/vp.2019.20521},
	url = {https://doi.org/10.21595/vp.2019.20521},
	year = 2019,
	month = {mar},
	publisher = {{JVE} International Ltd.},
	volume = {22},
	pages = {112--117},
	author = {Hamdy M. Youssef and Najat A. Alghamdi},
	title = {Three-dimensional biological tissue under high-order effect of two-temperature thermal lagging to thermal responses due to a laser irradiation},
	journal = {Vibroengineering {PROCEDIA}}
}

Copy Bibtex

Copied to clipboard!

[1]H. M. Youssef and N. A. Alghamdi, “Three-dimensional biological tissue under high-order effect of two-temperature thermal lagging to thermal responses due to a laser irradiation,” Vibroengineering PROCEDIA, vol. 22, pp. 112–117, Mar. 2019, doi: 10.21595/vp.2019.20521.

Copy IEEE

Copied to clipboard!

Youssef, Hamdy M., and Najat A. Alghamdi. “Three-Dimensional Biological Tissue under High-Order Effect of Two-Temperature Thermal Lagging to Thermal Responses Due to a Laser Irradiation.” Vibroengineering PROCEDIA 22 (March 15, 2019): 112–17. https://doi.org/10.21595/vp.2019.20521.

Copy Chicago

Copied to clipboard!

Three-dimensional biological tissue under high-order effect of two-temperature thermal lagging to thermal responses due to a laser irradiation

Abstract

1. Introduction

2. Materials and method

3. The governing equations in the Fourier transform domain

4. Results

5. Discussion

6. Conclusions

References

Cited by

About this article

Related Articles