Fissure prediction based on wavelet transform and complex signal analysis technology

1. Introduction

The unfavorable geological development of karst areas in China is very extensive, especially in Southwest China. Currently, more and more tunnels have been under construction in such areas, with Western Development and national economy developing rapidly. It’s dangerous to engineer under the risk induced by fissure, and the security of both workers and projects cannot be ensured, with bad effects of environments following. To avoid abandoning the developing tunnels and changing them to another track, it has been essential a lot to make accurate predictions about fissure [1-4].

Based on the problem of fissure outburst, the scholars take a variety of methods to forecast the wave in front of the tunnel face. For instance, hydrogeological analysis method, transient electromagnetic method, resistivity method, ground penetrating radar (GPR) method, Infrared detection method and so on. What’s more, the GPR method is one effective tool for predicting the groundwater of the kind mentioned, it’s a preferably method to forecast the fissure in front of the tunnel face as well nowadays [5].

Functional signal process mode is required for GPR to detect unfavorable geological body underground correctly. At present, signal processing technology has become mature after decades of development, such as classical Fourier spectrum analysis. However, when applying GPR to detect fissure, for the heterogeneity of underground medium, signals transmitted by radar will be attenuated by the absorption of the medium during the propagation, and will be refracted or reflected by the differences of dielectric constant. The signals above add together, making it burdensome to process the data, with the various interference adding, as a result it’s not easy to get preferable consequences applying Fourier spectrum analysis.

The Complex Signal Analysis Technology: collect multiple arguments’ profiles, starting from the three aspects of instantaneous amplitude, instantaneous phase and instantaneous frequency of reflected wave to study the abnormal information of radar signals, so we can make effective predictions of fissure. However, the technology magnify random noise when the instantaneous parameters are acquired, especially when the instantaneous frequency of complex signals are acquired.

To solve the problem, this paper proposes a method to improve the accuracy of fissure prediction by combining wavelet transform and complex signal analysis. In this method, wavelet transform can effectively suppress the noise, when there is no large loss of signal instantaneous frequency. The structure of this paper is arranged as follows, in the second section, the principle of complex signal analysis technique to predict karst fissure water is derived; in the third section, the wavelet transform is analyzed; the fourth section verifies the effectiveness of the proposed method; finally, the conclusion is given in the fifth section.

2. Prediction of fissure by complex signal analysis

The reflected signal received by the radar antenna can be expressed as:

$t$ is the time variable, $A\left(t\right)$ refers to the amplitude, which is related to the radiation intensity of the transmitting antenna, the receiving sectional area of the receiving antenna, the underground medium absorption coefficient, and the instrument gain, ${\omega }_0$ is the centered frequency, $\phi \left(t\right)$ is the phase position of$m\left(t\right)$.

According to Eq. (1), the amplitude, phase, frequency and other parameter information are contained in a unified real signal. It is difficult to get the change rule of single parameter from the change of real signal, which affects the accuracy of karst fracture prediction.

Complex signal analysis is a signal processing technology that extracts the instantaneous amplitude, instantaneous phase and instantaneous frequency of the real signal received by the radar through a series of operations in the time domain. The first step of acquiring complex signals is to carry out Hilbert transformation on real signals received by radar.

The Hilbert transformation of the real signal can be expressed as:

The frequency response of $h\left(t\right)$ with the Fourier transform is:

So the Hilbert transformation of $m\left(t\right)$ in the frequency domain can be expressed as:

$H\left(\omega \right)$ is called Hilbert filter, the amplitude-frequency characteristic is all-pass type, and the phase-frequency characteristic is $-\pi /2$ phase shift:

According to the real signal $m\left(t\right)$ and its Hilbert transformation, a complex signal can be obtained, as shown in Eq. (5).

$s\left(t\right)$ is the complex signal representation of the real signal $m\left(t\right)$ received by the radar, $A\left(t\right)$ is the instantaneous amplitude of the complex signal $s\left(t\right)\text{,}$$\theta \left(t\right)=\left({\omega }_{0}t+\phi \left(t\right)\right)$ is the instantaneous phase of the complex signal. The derivative of $\theta \left(t\right)$ with respect to time is the instantaneous frequency of the complex signal $s\left(t\right)$, as shown below:

In the case of little change about $\phi \left(t\right)$, $d\phi \left(t\right)/dt$ can be approximated as a constant $K$. At this point, the instantaneous frequency $\omega \left(t\right)$ of the complex signal $s\left(t\right)$ depends only on the central frequency ${\omega }_0$, Eq. (6) can be converted into:

Instantaneous amplitude of complex signal can be understood as an intuitive description of the reflected signal energy received by ground penetrating radar. According to the variation of instantaneous amplitude, we can infer the trend of energy loss caused by the transmission distance, the absorption of energy of the medium and the dielectric constant among the media. When the signal reaches the contact surface of different geological bodies, for the prominent difference of dielectric constants between them, the instantaneous amplitude changes, so we can judge the information like forms or something else of underground geological bodies on the basis of the variation of the instantaneous amplitude.

The instantaneous phase of complex signals the can be used to measure the continuity of the phase axis in GPR profiles, which will change strikingly in the anomaly of underground media and show an obvious discontinuity in the profile graph, thus, we can apply the instantaneous phase to forecast the abnormality underground. As there are phase discontinuities in instantaneous phase profiles, there exist abnormalities. The instantaneous phase is independent of the energy of the transmitted signal, so no matter how strong or weak the signal is, the instantaneous phase information will appear stably in theory.

The instantaneous frequency of complex signal can be obtained by derivation of the instantaneous phase. Numerically, it is related to the central frequency of the reflected signal. When the transmitted signal reaches the dielectric surface, the reflected signal will be reduced for the medium absorption effect. On the basis of the numerical value and the speed of change of instantaneous frequency, the information of geological body can be determined.

3. Improving prediction accuracy by wavelet transform

To make effective forecasts on fissure, we can apply complex analysis to GPR in prediction, extract profiles of a number of parameters, and start from the three aspects of instantaneous amplitude, instantaneous phase and instantaneous frequency of reflected wave to study the abnormal information of radar signals. However, it is inevitable to generate noise signals when using GPR in practice, and the noise signals will be amplified, especially when contracting the instantaneous frequencies of complex signals, leading a large amount of valid information covered by noise, as a result, it become burdensome to analyze the signals, and the accuracy is affected.

In recent years, wavelet theory has been widely used in the field of denoising. The wavelet transform is based on the characteristic that the time and frequency are delocalized. The frequency component remains the same on the time axis. The frequency conversion does not affect the linearity of the signal, which show the time characteristics and frequency characteristics at the same time [6-11]. Therefore, on the basis of complex signal analysis technology, wavelet transform is introduced to deal with the noise processing problem in this paper.

Wavelet is small area wave. It is a special wave with finite length and zero mean value. In the time domain, there are two characteristics of Compact Support or approximate Compact Support and Positive-and-negative-alternately volatility.

For a given signal $f\left(t\right)\in L^2$, we call:

as the wavelet transform of signal $f\left(t\right)$. $a$ is a factor of shrinkage or a scale factor, and $b$ is a shift factor. For the variability of $a$ and $b$, the wavelet has time-frequency localization characteristics. Thus, it demonstrates an unique analytical capability for non-stationary signals. During the wavelet analysis, window of wavelet ${\psi }_{\left(a,b\right)}\left(t\right)$ gradually widen with the scale factor $a$ increasing. Considering a wide range of time axes, it is equivalent to using low frequency wavelet to do profile analysis in frequency domain; for higher frequency noise signals, filtering capability is also enhanced.

The wavelet factors represent the approximation of wavelet functions and analysis signals: the larger the wavelet factor is, the closer the signal is to the wavelet function waveform meanwhile. It contains more noisy signals at lower scales, and contains more analytical signals at large scales, so the summation of wavelet factors at different scales can amplify the original signal and strengthen signals that are difficult to recognize in noise, consequently, the signals covered by the original signals are discovered.

There is no uniform standard for the selection of wavelet bases at present. However, the closer the graph of the transformed signal is to the wavelet figure, the more effective the denoising process is according to experience. Besides, when wavelet bases are selected, the orthogonality, compact support, symmetry and smoothness of wavelet should also be considered. According to the analysis of [12], this paper chooses wavelet mexh as the wavelet base of denoising.

4. Experimental analysis

In this section, the validity of the proposed method is verified by the measured data. The detection USES a 100 MHz central frequency antenna, and the sampling point is 512. The schematic diagram of line layout is shown in Fig. 1.

Fig. 2 shows the processing results of the complex signal analysis technique, in which Fig. 2(a) shows the instantaneous amplitude profile, Fig. 2(b) shows the instantaneous phase profile, and Fig. 2(c) shows the instantaneous frequency profile. As can be seen from Fig. 2, some effective information is submerged in noise, and it is difficult to see anomalies from the profile (especially the instantaneous frequency profile). Therefore, it is necessary to adopt wavelet transform to improve the prediction accuracy.

Fig. 1Map of GPR survey line

Fig. 3 is the result of the wavelet filtering. Comparing Figs. 2 and 3, we can see that the wavelet transform can improve the prediction accuracy, and the abnormal region is shown in Fig. 3.

After further construction verification, area 2, 3 is the kasrt-fractured water, and area 1 is karst cave. It coincides with the prediction result. It verifies the feasibility and accuracy of this method to predict fissure.

Fig. 2Processing results of complex signal analysis

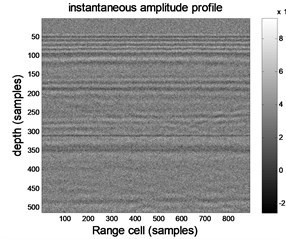
a) Instantaneous amplitude profile

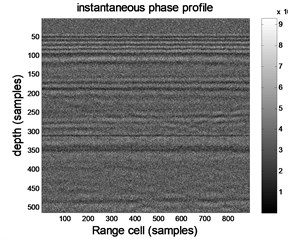
b) Instantaneous phase profile

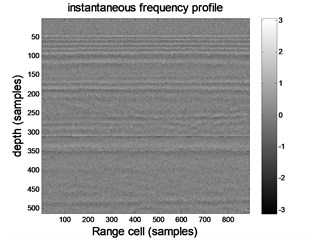
c) Instantaneous frequency profile

Fig. 3Processing results of wavelet transform

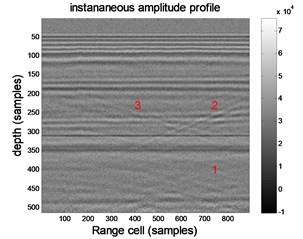
a) Instantaneous amplitude profile

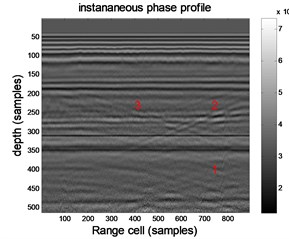
b) Instantaneous phase profile

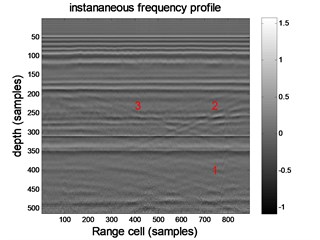
c) Instantaneous frequency profile

5. Conclusions

On the basis of complex signal analysis technology, wavelet transform is introduced to deal with the noise problem in this paper. First, use the complex signal analysis technology to make a comprehensive judgment on the abnormal information in the radar signals based on instantaneous amplitude, instantaneous phase and instantaneous frequency. Then, aiming at the problem that amounts of valid information is covered by noise when make forecast on fissure using complex signal analysis, the wavelet filtering is used to denoise the processing results of complex signal analysis technology, so as to improve the accuracy of fissure prediction. At last, an engineering example is given to illustrate the effectiveness of the proposed method.