Dynamical model of a fault phenomenon and reliability analysis for a circuit breaker in a vibration environment

1. Introduction

A circuit breaker not only is a basic low voltage device but also is an important kind of switch used in power system. Shown in Fig. 1(a), a circuit breaker is installed on the wall of an electrical box. From Fig. 1(b), the breaker is consisted of two contacts. One is the moving contact; the other is the fixed contact. If the two contacts are closed, then the electricity is turn on. When the two contacts are kept away, the electricity is turn off. Because of that, the breaker can turn on, bear and break the normal or overloaded current in a circuit within limited time. Therefore, it is widely used in the industrial installations, for example, rail systems, electric vehicles and ship fields. However, once there is a fault phenomenon for the circuit breaker system, the system doesn’t work properly. To improve instantaneous protection reliability, an instantaneous failure mechanism of low voltage circuit breakers was analyzed [1]. Especially in a complex environment (a vibration caused by the external disturbance), the breaker has a higher chance of being in a failure state. A vibrational analysis was carried out by analyzing the signal in the time-frequency domain under no-load switching operations with a commercially available high-voltage puffer-type circuit breaker without opening its major parts [2]. So, describing the fault phenomenon of a circuit breaker in the vibration environment is very necessary for improving security in industrial electrical equipment.

For the failure property of the circuit breaker, there were several methods proposed by many researchers. The most common method was empirical mode decomposition (EMD). For example, based on EMD method and support vector machine (SVM), a new method for the fault diagnosis of high voltage circuit breaker (CB) was proposed [3], an extraction method based on ensemble empirical mode decomposition (EEMD) was presented and was verified effectively by the practical examples for identifying the fault patterns of HV circuit breaker [4] and a new method based on improved empirical mode decomposition (EMD) energy entropy and multi-class support vector machine (MSVM) was proposed to diagnose fault for high voltage CB [5]. But this identification method couldn’t represent the mechanism of the fault phenomenon for the circuit breaker, because this fault property is often a kind of nonlinearity characteristic. Therefore, some innovative ways were presented in present years, an Expert System (ES) with the addition of a signal processor module and factual database module to the conventional ES has been proposed for the diagnosis of CBs and OLTCs [6]. A Least Squares Support Vector Machines (LS-SVM) based CB maintenance scheduling optimization approach that considers constraint of cost effect was proposed [7]. Furthermore, the application of vibration analysis was dealt successfully with for circuit-breaker (CB) diagnostic testing with the aim of detecting mechanical anomalies in CB drive mechanisms and other moving parts in the interrupting chamber [8]. However, regardless of which method was taken, a detailed force analysis must be implemented before studying the fault phenomenon for a circuit breaker.

In the paper, a circuit breaker in a vibration environment is simplified as a cart-inverted pendulum system, a dynamical model is proposed by the Newton’s Second Law. And some simulations and experiments are carried out to verify the nonlinear model. Obviously, the model is demonstrated to be feasible. The rest of this paper is organized as follows: a dynamical model for a circuit breaker with an external vibration disturbance is obtained by describing its failure phenomenon in Section 2. Some simulation and experiment results are shown and some discussions are presented in Section 3. Finally, some conclusions are given in Section 4.

Fig. 1A circuit breaker

a)

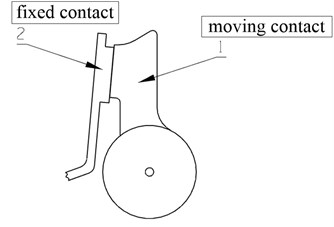
b)

2. Description for the fault phenomenon of the breaker system

In the paper, by simplifying the circuit breaker system, a dynamic model with mechanical analysis is presented for describing the nonlinearity of a low voltage circuit breaker under a vibration environment. Fig. 2(a) shows the circuit breaker system on a vibration desk. The vibration desk provides a vibration environment, such as a sinusoidal signal or a random signal. The beaker is fixed on the steel plate, and the fixation plate and the commodity shelf are installed on the vibration desk. Fig. 1(b) gives a detailed drawing of the breaker, and the label 1 and the label 2 represent the static contact and the moving contact of the breaker respectively. The static contact is fixed on the steel plate, but the moving contact can rotate around a fixed axle. Therefore, shown in Fig. 2(b), the vibration desk with fixation plate and the fixed contact is simplified as a cart applied with an external vibration disturbance $F$ on a smooth horizontal plane, while the moving contact is simplified as a rod leaning against the cart with a preloaded moment $T$. At a word, the circuit breaker in a vibration environment is simplified as a cart-inverted pendulum system.

The cart-inverted pendulum system is decomposed into a cart and an inverted pendulum, and their forces analysis is shown in the Fig. 3. For the cart in Fig. 3(a), according to Newton’s Second Law, the mechanical formulas along the $x$ and $y$ directions of the cart are expressed as:

where $x$ is the displacement of the cart along the horizontal direction, $M$ is the mass, $F_{Ax}$ and $N_B$ are the forces applied by the inverted pendulum’s A end and B end respectively, and $F_1$ and $F_2$ are the support forces by the ground. $c_1$ and $k_1$ are the damping coefficient and spring constant respectively. And $f_B$ is the friction.

Fig. 2Experimental setup and diagram of the breaker system

a)

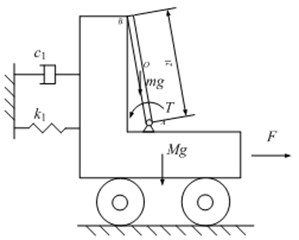
b)

Fig. 3Forces analysis of the system

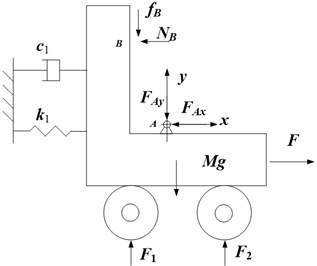
a)

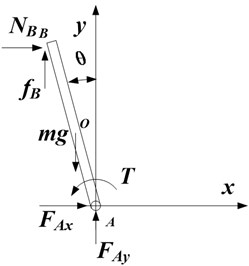
b)

Fig. 3(b) shows the forces analysis of the inverted pendulum, and the mechanical formulas are given as:

where:

$m$ is the mass of the inverted pendulum, $J$ is moment of inertia, and $l$ is half of the length of the pendulum. And $f_B=c_2{N}_B$. Moreover, $T$ is an average torque of the spring in the breaker and represents preload for the moving touch of the breaker, and $T$ maintains the stability of the vertical inverted pendulum by making the pendulum to lean against the car. Therefore, the acceleration at the O point of the pendulum is expressed as:

Combining Eq. (1), Eq. (2) and Eq. (3), then the dynamical equation is given as:

where $\delta$ represents that the B end of the inverted pendulum does or doesn’t get off the cart. If $\delta =$ 0, the moving contact has been kept away from the fixed contact for the circuit breaker. When $\delta =$ 1, the two contacts are closed, the breaker can work normally in the circuit system. The $\delta$ is expressed as:

For above description, a dynamical model is constructed for representing the fault property of a circuit breaker in power system under a vibration environment with forces analysis. In next Section, some simulations and experiments are performed to verify effectively the theoretical model, and some results will be discussed.

3. Simulation and experiment results

When a theoretical model (Eq. (4)) is established by some mechanics principles, some simulation and experiment results are gained to verify effectively the model. Therefore, by MATLAB/Simulink, the Eq. (4) is solved by ODE45 with the corresponding parameters of the model in Table 1, and some simulation verifications are gained. A sinusoidal acceleration (namely $F$/($M+m$) in Eq. (1) and Eq. (2)) applied on the cart. The sinusoidal signal is set at amplitude 0.5 m/s² and frequency 30 Hz. Then, the cart has a reciprocating motion, and the displacement $x$ of the cart is shown in Fig. 4. Under the sinusoidal force $F$ in Eq. (4), the displacement $x$ of the cart has a reciprocating value. And $\dot{\theta }$ isn’t all equal to zero. Therefore, it is obvious that a nonlinear relationship between the sinusoidal acceleration and the displacement $x$ of the cart is found. Moreover, for the displacement along the $x$ direction of the cart, the maximum amplitude is about 2.7 mm and the frequency is about 30 Hz.

Furthermore, the inverted pendulum has not only a reciprocating motion with the cart but also a rotational motion around point A on the cart in Fig. 3. Therefore, the point B of the inverted pendulum is viewed as that of the moving contact of the circuit breaker. And the initial angle ${\theta }_0$ is –5° (–0.0873 rad) when the inverted pendulum leans against the cart. Then when the cart suffers from an acceleration excitation, the whole inverted pendulum system has a motion. At the same time, the point B is separated from the cart and the inverted pendulum is rotating clockwise. However, the inverted pendulum is pulled back by the initial moment $T$. That causes the intermittent contact between the point of the inverted pendulum and the cart. The intermittent contact will affect the work efficiency and life of the break in the mechanical equipment. Therefore, the displacement of the point B is shown is shown in Fig. 5 by a formula $x_B=x+2l\times \mathrm{s}\mathrm{i}\mathrm{n}\left(\theta \right)$. The rotational angle $\theta$ is displayed in Fig. 6 when the point B of the inverted pendulum is far from the cart. Apparently, the rotational angle $\theta$ keeps a constant value –0.0873 rad in a half period when the two contacts are closed. Moreover, the two contacts are opening, and the angle is more than the initial angle ${\theta }_0=$ –5° (–0.0873 rad) when the moving contact is far from the cart in the vibration environment.

Fig. 4Displacement x of the cart

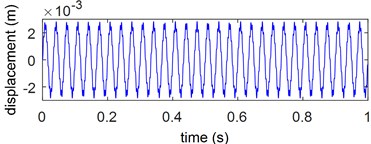
Fig. 5Displacement xB of the point B in the inverted pendulum

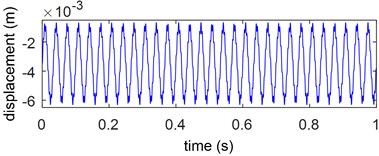
Fig. 6Rotational angle θ of the inverted pendulum

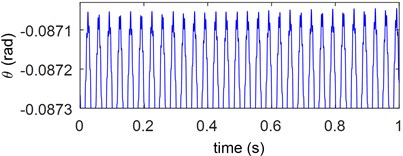
Fig. 7Circuit diagram of the breaker

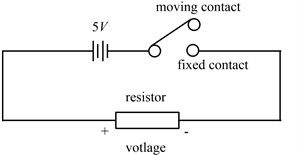
Then the circuit breaker is put in the vibration environment and its contacts are open, shown in Fig. 7. The circuit is viewed as a switch with a moving contact and a fixed contact. When the contacts are closed, the voltage is about 5V. Moreover, when the contacts are far away, the voltage of the resistor is about 0V. If the angle $\theta$ > –5°, the breaker is open and $\delta$ is equal to 0; if the angle $\theta$ ≤ –5°, the breaker is closed and $\delta$ is equal to 1. Furthermore, the voltage of resistor is measured by NI collector. The simulation and experiment results are revealed in Fig. 8. It shows the voltage of the resistor in Fig. 7. When the sinusoidal vibration acceleration is applied on the vibration platform (simplified as a cart in Section 2), the blue line is gained from the model by MATLAB/Simulink and the red dotted data is collected from the experiment. From fitting ration of the blue and red data, the theoretical model can describe effectively the experiment phenomenon.

Fig. 8Voltage of the resistor

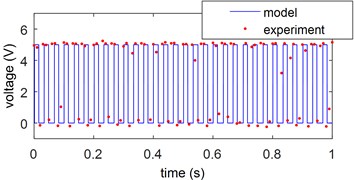
Fig. 9Minimum acceleration amplitude in different frequency

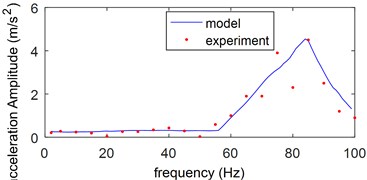
When an acceleration signal is set at a constant frequency and is applied on the cart, the limit amplitude of the acceleration is obtained to keep the moving contact away from the fixed contact of the circuit breaker by some simulations and experiments. The limit acceleration amplitudes in different frequency are given in Fig. 9. The minimum amplitude value of the acceleration to open the breaker under a vibration environment was attained with a different frequency and the minimum amplitude has a peak value at about 85 Hz. The limit value is helpful to set a standard for the reliability of the low voltage breaker under a vibration environment. It is evident that the experimental results are in good agreement with that model results.

4. Conclusions

In the paper, a fault phenomenon of the circuit breaker is described in vibration environment. By the mechanics analyses, the circuit breaker in the vibration environment is simplified as a cart-inverted pendulum system which is applied a vibrational force. Through the Newton’s Second Law, a theoretical model is proposed for the inverted pendulum system. By the simulation in MATLAB, the displacements of the cart and the inverted pendulum are nonlinear. And when the rotational angle of the inverted pendulum is various, the moving contact is kept away from the fixed contact of the circuit breaker. The fault property of the breaker is demonstrated by the theoretical model and the experiment. In future work, some methods will be studied and designed to avoid the fault phenomenon for the circuit breaker.