Assessing multiple cracks in beams by a method based on the damage location coefficients

1. Introduction

For decades, the evaluation of structural integrity based on vibration analysis is a major concern of the researchers. In this regard, numerous techniques that permit assessing the size and position of a crack in the beam exist. They consider either the change in the natural frequencies, mode shapes, modal curvatures or modal damping [1-4]. The most commonly used modal parameter is the natural frequency, which is easy to measure and does not require complex or sensitive equipment. The mathematical relationship between the damage parameters, i.e. the location and severity, and the frequency decrease is presented in the papers [5-7]. Several correction coefficients to be applied for changing environmental conditions as the temperature or moisture were also presented in the literature; see for instance references [8, 9]. Usually, the frequency change caused by cracks compares to those achieved by using theoretical models. If more vibration modes are involved, the comparison is made by using dissimilarity estimators that perform a bin-by-bin evaluation [10-12]. It is possible to separate the problem of finding the crack location and severity by applying two consecutive normalizations [13]. Initially, the location is determined involving the Damage Location Coefficients (DLC). Afterward, the severity is found for the crack for which the location is identified [14].

When the beam is harmed by more than one crack, directly using the DLC is not possible because the cracks can have different positions and severities. Studies dedicated to the detection of multiple cracks are present in the literature [15, 16]. The key finding is that the superposition principle applies for most damage locations, but not for close located cracks [17].

We propose in this paper an algorithm to find the location of multiple cracks and show how it can be implemented in Visual Basic for Application in Excel to automate the damage assessment process. The functionality of the algorithm is tested for the frequencies obtained by means of the finite element method (FEM) for the healthy beam and a series of simulated damages.

2. Theoretical background

Let us consider a beam with the left end fixed end the right end free, i.e. a cantilever beam. This beam has, for all transverse vibration modes $i=$ 1, ..., $n$, known natural frequencies $f_{i_U}$. We can also calculate the modal curvatures ${\varphi }_i^{\text{'}\text{'}}\left(c\right)$ at any distance $c$. It was shown in [6] that the frequency $f_{i_D}(c,d)$ of a beam with a transversal breathing crack can be calculated as:

where $d$ is the damage depth and the curvature is normalized by division with the value found at the location where it achieves the maxima. For the cantilever, this location is the fixed end. The term $\gamma (0,d)$ in Eq. (1) is the damage severity, calculated from the energy loss with the mathematical relation:

The frequency shift caused by the described crack can be deduced from Eq. (1), as:

and subsequently the Relative Frequency Shift (RFS) as:

when calculating $n$ values for the RFS of a damaged beam, we obtain the sequence:

We can observe that by dividing all terms in the row matrix with the biggest one of the sequence, the severity is eliminated and all terms achieve values lower than one:

We nominate the sequence in Eq. (6) as Damage Location Indicator (DLI) and the individual terms as Damage Location Coefficients (DLC). The DLI depend just on the crack position $c$, therefore the problems of finding the crack location and its severity are separated. Knowing the mode shapes, it is easy to calculate the DLI for any location on the beam and develop a database with possible scenarios. If we measure periodically the natural frequencies of a beam and find alteration, we can calculate in a similar way the terms in Eq. (6). These values, achieved from experiments, are also free of information regarding the damage severity. We nominate these values, which clearly indicate the damage position, as Damage Signature (DS). By simply comparing the DS with the DLIs for a lot of locations $c$, we find the two that fit and the corresponding distance $c$ which indicates the crack position.

3. The proposed algorithm

Separating the problems of finding the crack location and its severity is not possible if more cracks are present in the beam, because these can achieve different severities. We have shown in [18] that Eq. (1) can be applied twice when two cracks at locations $c_1$ and $c_2$ that have depths $d_1$ and $d_2$ affect the beam. This is based on the equivalent healthy beam theory we developed for single cracks. In fact, it is as we apply Eq. (1) to a healthy beam with the frequency $f_i\left(c_1,d_1\right)$. Therefore, we can write:

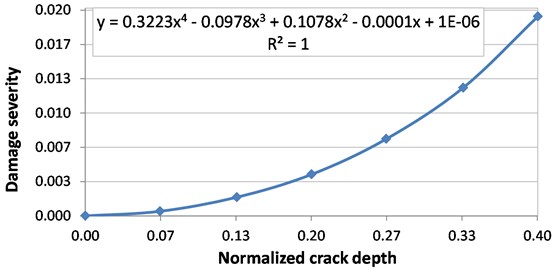
The algorithm we describe in this section has implemented Eq. (7). Based on this algorithm, we develop a database containing the frequencies for the first nine transverse vibration modes for the healthy beam and the beam with one and two cracks. These cracks, simulated in the beam with thickness $H$, achieve $m$ depths $d_k$, thus $k=$ 1, ..., $m$. We show in Fig. 1 the severity evolution with the normalized crack depth derived by means of FEM simulations that cover the range $d$/$H=$ 0/0.4. In this figure is also given the regression curve, which permits calculating the severity for any crack depth. This relationship is valid for all rectangular cross-sections, depending exclusively on the ratio $d$/$H$. To create the database, for all damage depths, the resulted cracks are removed along the beam with a step $s=$ 0.005/$L$, resulting in $r=$ 200 crack locations. The index of an individual crack is denoted $j$, which takes values $j=$ 1, ..., $r$.

Fig. 1Damage severity evolution with the crack depth growth

The database is developed using Visual Basic for Application in Excel. First, damage scenarios by considering just one crack with different severities and locations are created and one row is assigned in the database for each case. In addition, we insert rows for all possible combinations resulted when two cracks affect the beam. The frequencies for all cases are calculated with Eq. (7).

The first section of a row in the database, carrying the basic information about the damages and the predicted frequencies is presented in Table 1. The first column indicates the index of the damage case, $h=$ 1, ..., $q$, the next four columns describe the simulated cracks and the following nine columns indicate the resulted normalized frequencies for the nine vibration modes.

Supplementary, from the natural frequencies we calculate the RFS for all damage cases and vibration modes, by using the mathematical relation:

One observes that Eq. (4) is not anymore used, because we have more depths and curvatures. We can introduce in the application measured data in terms of frequencies and calculate the damage signatures $D{S}_i$ with a mathematical relation similar to Eq. (8). A view on the second section of a row in the database is shown in Table 2. Note that, in the database each row contains other RFS but the same DS.

Step by step comparison between all RFS and the DS is made involving the Euclidean distance that is, for the damage case $h$, calculated as:

In the above equation, all combinations of crack depths and locations are considered for both cracks. The aim is finding the index $h_{min}$ for which the $E{D}_h$ sequence attains the minima.

4. Numerical experiments

The reliability of the algorithm is tested for frequency responses obtained by means of FEM. The test specimen is a cantilever steel beam with the following geometry: length $L=$ 1000 mm, width $B=$ 50 and a thickness $H=$ 5 mm. We carry out simulation using the ANSYS software. The mechanical properties are assigned for the cantilever beam from the ANSYS Workbench library and correspond to the structural steel. We present these values in Table 3.

To ensure results with a high degree of generality, we consider three damage cases:

– Case 1, with $c_1=$ 160 mm and $d_1=$ 1 mm, respectively $c_2=$ 100 mm and $d_2=$ 1 mm;

– Case 2, with $c_1=$ 160 mm and $d_1=$ 1 mm, respectively $c_2=$ 100 mm and $d_2=$ 1.67 mm;

– Case 3, with $c_1=$ 160 mm and $d_1=$ 1 mm, respectively $c_2=$ 700 mm and $d_2=$ 1 mm.

All cracks go through the whole beam width and have a 0.005 mm distance between the opposite faces, thus are open cracks. The discretization is made using hexahedral elements with maximum edge dimension 2 mm. The results achieved by simulation are presented in Table 4. For the mentioned crack locations, we performed modal analysis to find the first nine natural frequencies for the transverse vibrations.

Next, we calculate the DS for the four damage cases and perform dissimilarity analyses by involving Eq. (9). For the calculus we used ten severities, associated with nine equidistantly distributed crack depths. We found the minima for the three damage cases, which indicate the crack parameters.

We also tested if the DS fit the identified RFS or the minimum found by the dissimilarity test does not correspond to the real damage scenario. This is made by comparing the graphical representation of the RFS with the DS. Based on the diagrams in Fig. 3, we conclude that all damage parameters are correctly identified, except the location of one crack which is found with a 1 % error.

Fig. 3Comparison of the identified RFS with the DS of the three damage scenarios

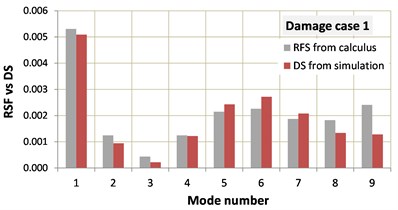
a)

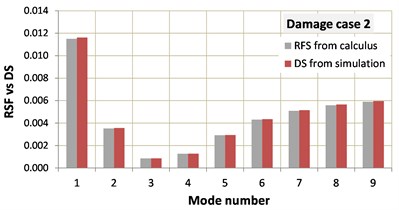
b)

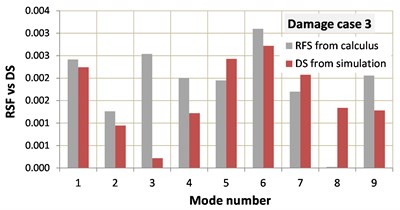
c)

5. Conclusions

The paper proposes and algorithm to assess multiple cracks in beams based on the analysis of the frequency shifts. Three damage scenarios involving cracks with different location and depth are selected to test its reliability. By applying the tests, we succeed to correctly assess all cracks, the achieved positions being indicated with an error less than 1 %, which means 10 mm.

By performing numerous tests, we also found that it is sufficient to take one hundred crack locations for constructing the database. This resolution ensures a sufficiently high precision in the location of cracks. On the other hand, increasing number of damage severities taken to create the database increase the precision of the cracks depth. Future research will be focused on optimizing the minima searching algorithm to reduce the time used for calculus.